行星齿轮箱典型故障对内齿圈齿根应变的作用机理研究

牛 杭， 张小栋1,, 赵欣丹， 侯成刚

(1. 西安交通大学 现代设计及转子轴承系统教育部重点实验室， 西安 710049；2. 西安交通大学 机械工程学院， 西安 710049)

行星齿轮箱典型故障对内齿圈齿根应变的作用机理研究

牛 杭2， 张小栋1,2, 赵欣丹2， 侯成刚2

(1. 西安交通大学 现代设计及转子轴承系统教育部重点实验室， 西安 710049；2. 西安交通大学 机械工程学院， 西安 710049)

行星齿轮箱由于具有优良的特性被广泛应用于多领域的机械传动系统中，但恶劣的工作条件导致其故障频发，因此开展行星齿轮箱故障诊断方法的研究工作十分必要。传统的基于振动信号的故障诊断方法在识别行星齿轮箱早期微弱故障方面具有局限性，为此提出基于内齿圈齿根应变信号的行星齿轮箱故障诊断方法，并主要开展行星齿轮箱典型故障对内齿圈齿根应变的作用机理研究工作。分析行星齿轮箱内齿圈齿根应变模型的构建方法，将内齿圈齿根应变模型分解为行星轮-内齿圈啮合力模型、内齿圈轮齿的齿形系数模型和齿间载荷分配系数模型；利用行星齿轮箱的纯扭转模型计算行星轮-内齿圈啮合力，利用材料力学理论推导内齿圈轮齿的齿形系数，并对行星轮-内齿圈啮合过程中的齿间载荷分配系数进行分析；研究行星齿轮箱典型故障对啮合刚度的影响，并根据内齿圈齿根应变模型计算得到典型故障下内齿圈齿根应变的变化规律。建模仿真计算分析结果表明，不同类型、不同部位、不同剧烈程度的故障会对行星齿轮箱内齿圈齿根应变信号造成不同影响，利用内齿圈齿根应变信号可有效识别行星齿轮箱的故障行为。

行星齿轮箱； 内齿圈； 齿根应变； 振动； 故障诊断

行星齿轮箱由于体积小、重量轻、传动效率高、承载能力强等优点被广泛用于航空航天、风力发电、起重运输等领域的机械传动系统中。通常行星齿轮箱工作在低速重载的恶劣环境下，其关键部件出现故障的概率很高，为了减少事故发生，降低维修成本，开展行星齿轮箱的故障诊断工作十分必要。

目前，行星齿轮箱的故障诊断方法主要是振动分析法。振动信号中包含有丰富的故障信息，是一种常用的机械设备故障特征载体信号，然而，行星齿轮箱的振动信号相比于一般机械设备具有更加复杂的特点。由于测量振动信号的加速度传感器在箱体上固定不动，而行星轮却在公转，所以传感器测到的多组振动信号的强度会被传输路径调制，并且由于各振动信号之间存在相位差[1]，当这些振动信号在传感器处相互耦合时，会出现矢量叠加效应，影响振动信号中各频率成分的幅值[2]，从而导致故障特征频率成分可能减小或消失；另外，变速、变载的工况会对振动信号的幅值造成影响，转速波动会使振动信号的频谱表现模糊，故障特征频率发生变化。由于行星齿轮箱振动信号的这种非线性和非平稳性特点，虽然近年国内外学者取得了一些非常有价值的研究成果[3-7]，但从实际工况下的振动信号中提取行星齿轮箱的早期微弱故障特征仍是一个技术难题。

从动力学角度分析不难发现，行星齿轮箱故障首先会造成啮合状态变化，进而才会导致振动信号变化，振动信号是反映啮合状态的一种间接信号。已有的研究表明行星齿轮箱振动信号与啮合状态信息之间具有非常复杂的映射关系，这种映射关系的复杂性本质上导致了基于振动信号的行星齿轮箱故障诊断方法的局限性。为了突破这一困境，除了继续深入开展上述研究外，寻找更加优质的故障特征载体信号将是一种更为有效的途径。

由于行星轮-内齿圈啮合状态会直接影响内齿圈齿根应变，行星轮-太阳轮啮合状态会通过行星轮间接影响内齿圈齿根应变，所以与振动信号相比，内齿圈齿根应变信号与啮合状态信息之间具有更加直观、明确的对应关系，理论上可以更好地反映行星齿轮箱的健康状态。本课题组自2003年起至今一直从事光纤动态检测技术的研究工作[8]，并于近两年提出了基于光纤光栅的齿根应变检测方法[9]，且就结构件应力应变的光纤光栅动态测量技术进行了实验研究[10]，该方法克服了现有的光弹法和电测法的不足，为内齿圈齿根应变的在线分布式测量提供了解决途径。本文将着重展开行星齿轮箱典型故障对内齿圈齿根应变的作用机理研究，旨在为基于内齿圈齿根应变的行星齿轮箱故障诊断方法提供理论依据。

在齿根应力应变研究方面，国内外学者多针对一对齿轮啮合的情况，分析不同设计参数对轮齿弯曲强度的影响[11-12]，这些研究没有从行星齿轮箱系统角度考虑问题，因此，难以解释行星齿轮箱故障和内齿圈齿根应变的关系。本文首先讨论行星齿轮箱内齿圈齿根应变的建模方法，然后分别对行星轮-内齿圈啮合力、内齿圈轮齿的齿形系数和齿间载荷分配系数等三个子模型进行分析研究，以完成内齿圈齿根应变模型的构建。最后，针对行星轮、太阳轮、内齿圈上存在的不同形式常见故障，通过仿真分析的手段，分别讨论不同类型、不同位置以及不同剧烈程度的故障对内齿圈齿根应变的影响。

1 内齿圈齿根应变建模方法研究

如图1所示，对于行星齿轮箱内齿圈某一轮齿ζ而言，其齿根应变由轮齿ζ的齿形以及分配到轮齿ζ的啮合力两个因素主要决定。

图1 行星齿轮箱结构示意图

轮齿ζ从进入啮合到退出啮合的过程中，啮合点位置变化，啮合刚度变化，导致行星轮-内齿圈啮合力以及轮齿间载荷的分配情况变化，所以即便外界载荷不变，轮齿ζ的齿根应变仍呈现时变特点，其模型如式(1)所示

ε(t)=KYF(t)Xr(t)Frpi(t)

(1)

式中:ε(t)为内齿圈某一轮齿的齿根应变；K为应变修正系数，该值为常数；YF(t)为齿形系数，描述不同啮合位置处的齿形信息；Xr(t)为齿间载荷分配系数，描述分配到内齿圈分析轮齿上的行星轮-内齿圈啮合力所占的比例；Frpi(t)为行星轮-内齿圈啮合力。

由式(1)可以看出，内齿圈齿根应变模型主要包含行星轮-内齿圈啮合力模型、齿形系数模型以及齿间载荷分配系数模型。以下分别针对上述三个子模型进行分析研究，以完成内齿圈齿根应变模型的构建。

2 行星轮-内齿圈啮合力模型

图2为2K-H型行星齿轮箱的一种纯扭转模型[13-15]，设行星轮数为N，则该模型有N+2个自由度，分别为太阳轮的扭转自由度us、行星架的扭转自由度uc、行星轮i的扭转自由度upi。

根据图2所示，行星轮i-内齿圈啮合力可表示为如(2)式所示形式

(2)

式中:krpi为行星轮i-内齿圈的啮合刚度；krpi为行星轮i-内齿圈的啮合阻尼，该值为常数；Urpi为行星轮i-内齿圈的啮合变形，Urpi=upi-uc。若求解Frpi，需得到krpi和Urpi随时间的变化规律。

图2 行星齿轮箱纯扭转模型

首先，建立行星轮-太阳轮和行星轮-内齿圈的啮合刚度模型。设S(2πft+φ,τ)为频率为f，初相位为φ，占空比为τ的方波信号，且ksp1的初相位为0，则行星齿轮箱的啮合刚度可以表示为如式(3)所示形式

(3)

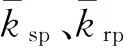
然后，求解行星轮i-内齿圈啮合变形Urpi。建立如式(4)所示的动力学模型

(4)

式中:J为转动惯量，下标s，c，pi分别表示太阳轮、行星架、行星轮i；Uspi为行星轮i-太阳轮的啮合变形，Uspi=us-upi-uc；cspi为行星轮i-太阳轮的啮合阻尼；mpai为行星轮i的质量；rs为太阳轮的基圆半径；rpi为行星轮i的基圆半径；rc为行星架半径；rbc为行星架的当量半径，rbc=rccosα，α为啮合角；TD为驱动转矩；TL为负载转矩。

式(4)所示方程中含刚体自由度，为了消除刚体位移，引入相对坐标Uspi和Usc，其中Usc=Uspi+Urpi。引入相对坐标后，式(4)转化为

(5)

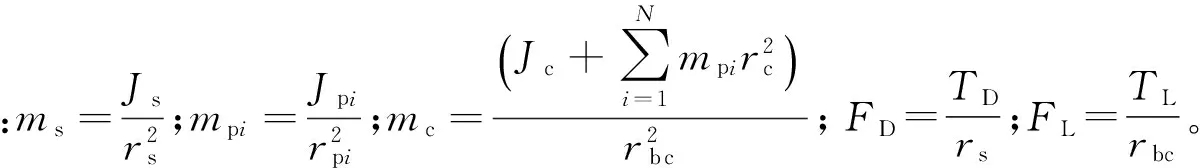
求解式(5)，得到Uspi、Usc，则行星轮i-内齿圈的啮合变形Urpi=Usc-Uspi。

最后，将由式(5)求得的Urpi和式(3)中的krpi代入式(2)，即可得到行星轮-内齿圈啮合力随时间的变化规律。

3 内齿圈齿形系数与齿间载荷分配系数模型

内齿圈上的单个轮齿的受力情况如图3所示。

将内齿圈轮齿等效为悬臂梁，根据材料力学理论，内齿圈齿根的应变(齿面方向)可表示为如式(6)所示形式

(6)

式中，B为轮齿宽度。定义齿形系数YF如式(7)所示

(7)

式中:齿根法向弦长S;弯曲力臂h根据ISO 6336-3—2006标准[16]计算。将式(7)带入式(6)，可得式(1)所示形式。

图3 内齿圈单个轮齿的受力情况

文献[17]通过对650组不同几何参数的内啮合传动进行计算分析，发现内啮合传动过程中的齿间载荷分配系数形式除与齿顶高相关外，与轮齿其他几何参数关系不大。对于标准齿顶高的情况，在内齿圈某一轮齿从进入啮合到退出啮合的过程中，其齿间载荷分配系数的形式如图4所示，其中t1为内齿圈某一轮齿进入啮合的时刻，t4为该轮齿退出啮合的时刻，t1-t2为双齿啮合区时间段，t2-t3为单齿啮合区时间段，t3-t4为双齿啮合区时间段。

图4 齿间载荷分配系数

4 典型故障下内齿圈齿根应变的变化规律分析

根据文献[18 ]和文献[19]，当正常轮齿(如图5(a))出现齿面剥落、轮齿缺损、裂纹故障(如图5(b)～图5(d))时，故障齿参与的啮合刚度可呈现出如图6所示的形式。

为了分析行星齿轮箱出现如图5(b)～图5(d)所示故障时内齿圈齿根应变变化特点，将图6所示的啮合刚度代入式(5)，利用4阶Runge-Kutta法求解Urpi，然后将Urpi和krpi代入式(2)求解内啮合力Frpi，最后将Frpi代入式(1)即能求解得到内齿圈齿根应变的变化规律。

(a)正常(b)齿面剥落

(c)轮齿缺损(d)裂纹

图5 正常轮齿与故障轮齿形态

Fig.5 Normal gear tooth and faul gear tooth

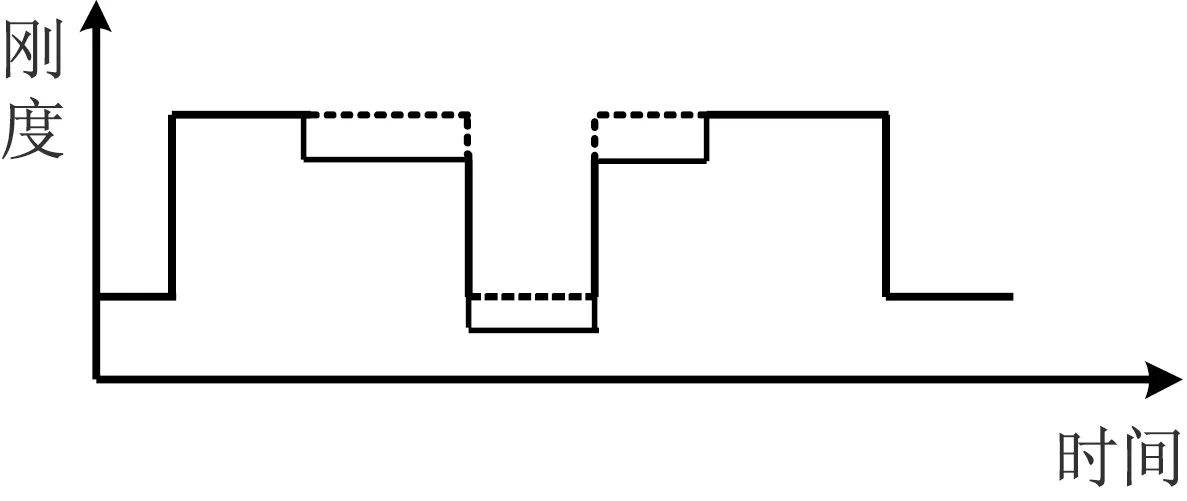
(a) 齿面剥落

(b) 轮齿缺损

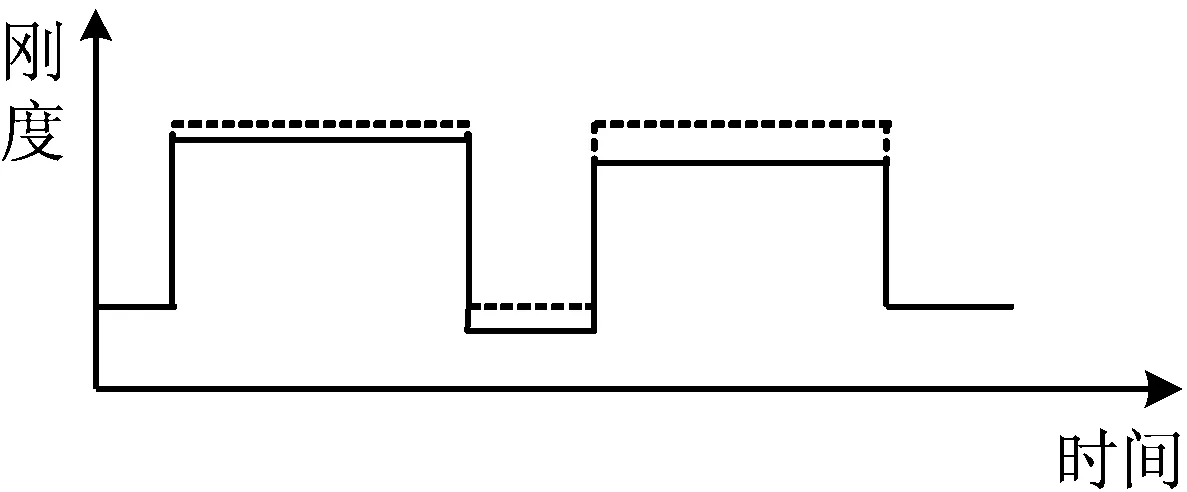
(c) 裂纹

本文所用到的行星齿轮箱参数如表1[20]所示。以下分析只针对与行星轮1发生啮合的内齿圈轮齿的齿根应变信号，与其他行星轮发生啮合，具有类似的分析方法。

4.1 行星轮故障对内齿圈齿根应变的影响

本节将讨论在行星轮1的某个轮齿上出现的齿面剥落、轮齿缺损和裂纹等三种常见故障。

(1) 行星轮局部故障在齿根应变信号中的特征频率分析

图7为当行星轮出现轮齿缺损故障后，内齿圈齿根应变的变化情况，图8为图7在0.55～0.73 s的局部放大图。从图8可以明显观察到行星齿轮箱的啮合频率40 Hz(0.025 s)，且当故障齿参与啮合时，由于啮合刚度局部减小，内齿圈齿根应变出现异常。从图7可以看出，在行星轮的一个自转周期(1.025 s)内，内齿圈齿根应变出现了时间间隔为半个行星轮自转周期(0.512 5 s)的两个异常位置，每个异常出现的频率为行星轮的自转频率(0.98 Hz)。这两个异常啮合出现的原因不同，第一个异常是由行星轮故障齿和内齿圈轮齿啮合导致的，第二个异常是由行星轮故障齿和太阳轮轮齿啮合导致的。对于齿面剥落和裂纹故障，其特征频率与轮齿缺损故障相同。

图8 行星轮故障时内齿圈齿根应变信号局部放大图

(2) 故障类型对齿根应变偏差的影响分析

针对不同的行星轮故障，内齿圈齿根应变异常形式是有明显区别的。首先将相邻的齿根应变信号相加，形成时域上连续的齿根应变信号，然后求正常的齿根应变连续时域信号与故障下的齿根应变连续时域信号的偏差。

图9所示为在三种故障下，当行星轮1的故障齿与内齿圈发生啮合时，内齿圈齿根应变信号的偏差。从图9可以看出，不同行星轮故障对内齿圈齿根应变信号的影响不同，每种故障所对应的齿根应变偏差与相应的时变啮合刚度(如图6)在形式上有一定的相关性，所以可以根据内齿圈齿根应变偏差的形式判断不同的行星轮故障类型。

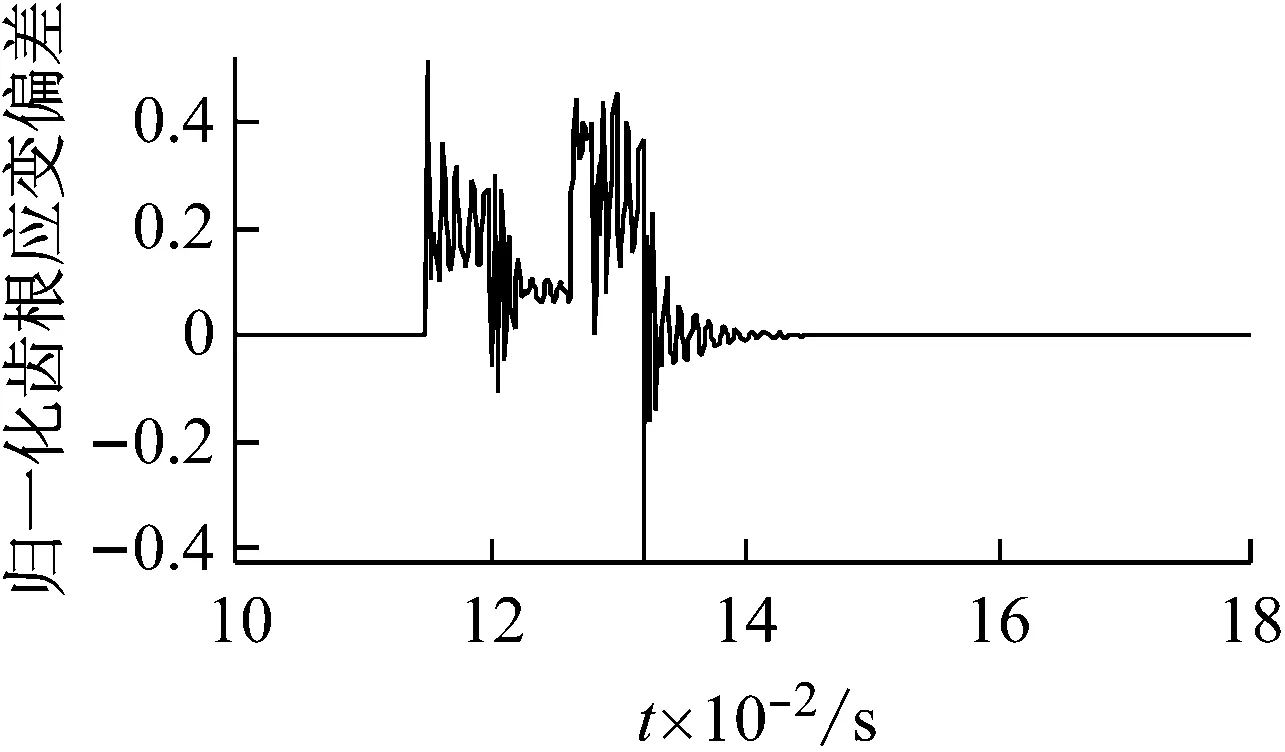
(a) 齿面剥落

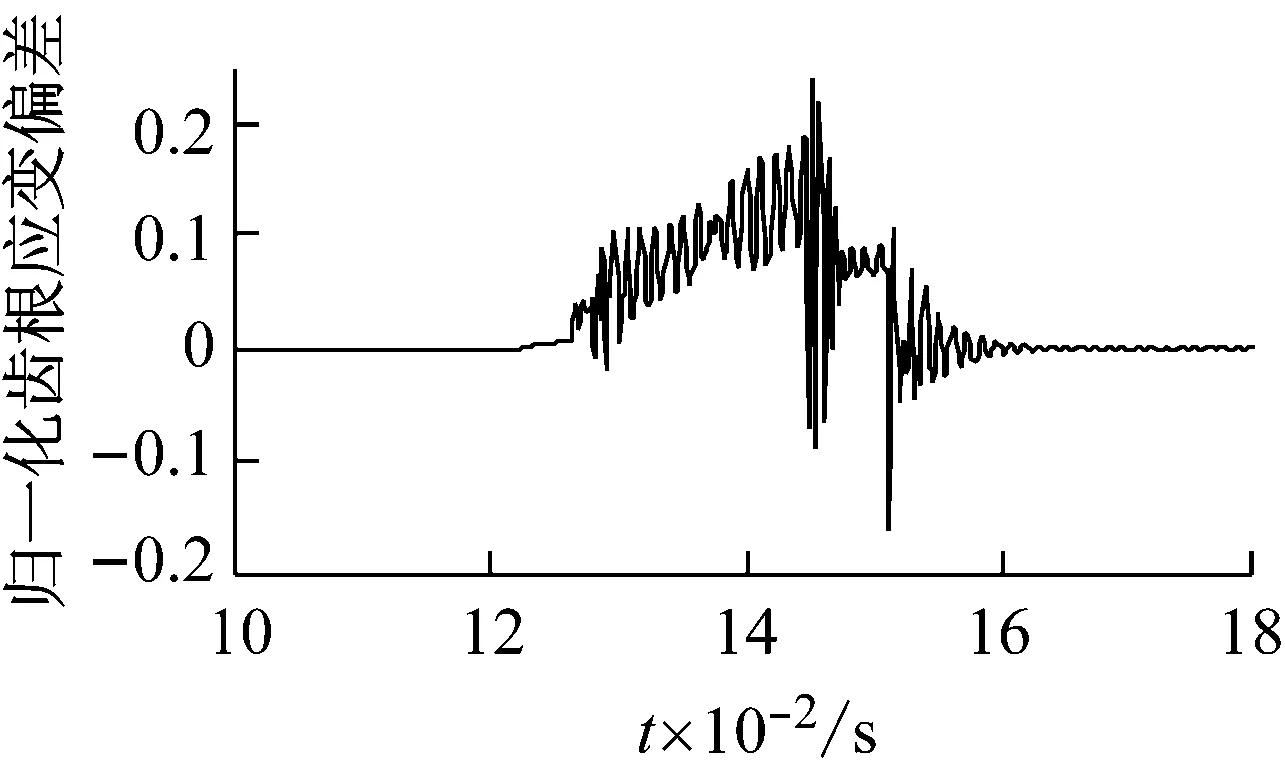
(b) 轮齿缺损

(c) 裂纹 图9 不同行星轮故障下内齿圈齿根应变偏差

(3) 故障剧烈程度对齿根应变偏差的影响分析

针对行星轮的某一轮齿上分别存在的三种深度不同的裂纹，其对啮合刚度的影响如图10所示。

图10 不同裂纹深度对啮合刚度的影响

按照前文所述方法计算在三种故障剧烈程度下内齿圈齿根应变偏差，如图11所示。由图11可知，故障越剧烈，齿根应变偏差的能量水平越高，根据这一特点，有望实现行星齿轮箱故障的定量识别。对于齿面剥落和轮齿缺损故障，其不同剧烈程度下齿根应变信号的表现规律与裂纹故障相同。

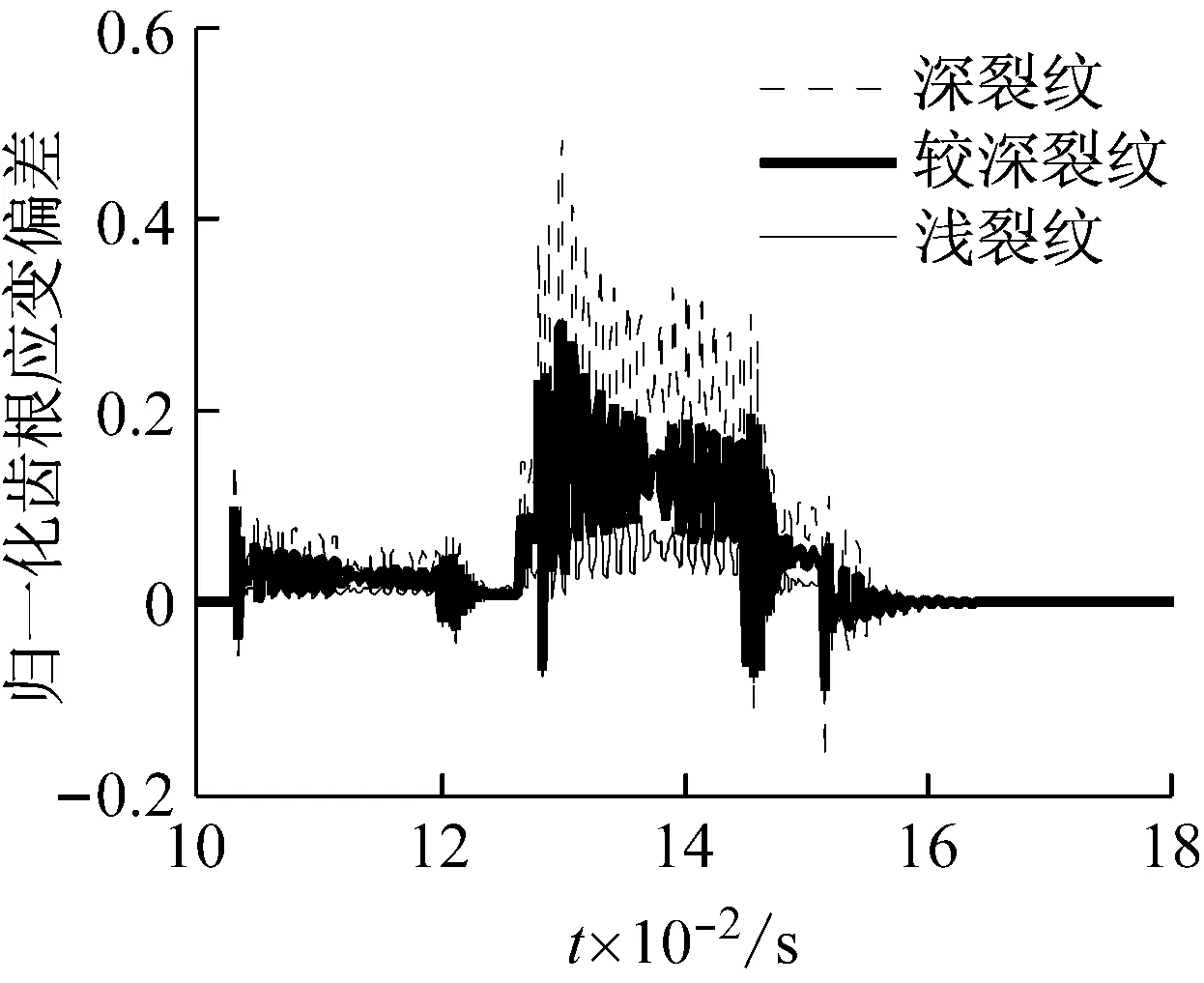
图11 不同裂纹深度下内齿圈齿根应变偏差

4.2 太阳轮故障对内齿圈齿根应变的影响

本节将讨论在太阳轮的某个轮齿上出现的齿面剥落、轮齿缺损和裂纹等三种常见故障。

图12为当太阳轮出现轮齿缺损故障后，内齿圈齿根应变的变化情况。由图12可知，在太阳轮相对于行星架的一个旋转周期(0.55 s)内，内齿圈齿根应变出现了时间间隔为1/3个太阳轮相对旋转周期(0.18 s)的三个异常位置，每个异常出现的频率为太阳轮的相对旋转频率(1.8 Hz)。其中，第一个异常是由太阳轮故障齿和行星轮1啮合导致的，第二个异常是由太阳轮故障齿和行星轮2啮合导致的，第三个异常是由太阳轮故障齿和行星轮3啮合导致的。

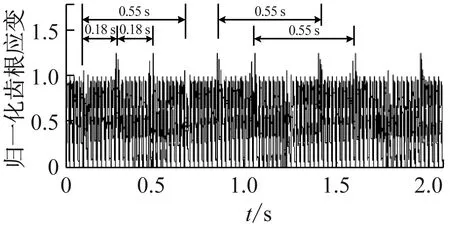
图12 太阳轮故障时内齿圈的齿根应变信号

图13所示为在三种故障下，当太阳轮故障齿与行星轮2发生啮合时，内齿圈齿根应变信号的偏差。由图13可知，不同太阳轮故障对内齿圈齿根应变信号的影响不同，每种故障所对应的齿根应变偏差与相应的时变啮合刚度有一定的相关性，所以可以根据内齿圈齿根应变偏差的形式判断不同太阳轮故障的类型。

对于太阳轮故障，当故障剧烈程度不同时，内齿圈齿根应变信号的表现与行星轮故障具有相同的规律，在此不再详述。

4.3 内齿圈故障对内齿圈齿根应变的影响

本节将讨论在内齿圈的某个轮齿上出现的齿面剥落、轮齿缺损和裂纹等三种常见故障。

图14为当内齿圈出现轮齿缺损故障后，内齿圈齿根应变的变化情况。由图14可知，在行星架的一个旋转周期(2.6 s)内，内齿圈齿根应变出现了时间间隔为1/3个行星架旋转周期(0.87 s)的三个异常位置，每个异常出现的频率为行星架的旋转频率(0.38 Hz)。其中，第一个异常是由内齿圈故障齿和行星轮1啮合导致的，第二个异常是由内齿圈故障齿和行星轮2啮合导致的，第三个异常是由内齿圈故障齿和行星轮3啮合导致的。

(a) 齿面剥落

(b) 轮齿缺损

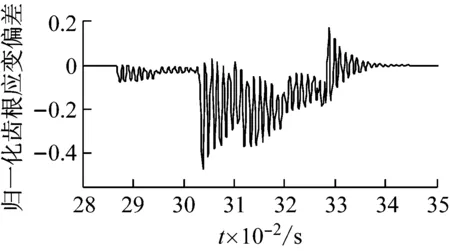
(c) 裂纹

图14 内齿圈故障时内齿圈的齿根应变信号

图15所示为在三种故障下，当内齿圈故障齿与行星轮2发生啮合时，内齿圈齿根应变信号的偏差。由图15可知，不同内齿圈故障对内齿圈齿根应变信号的影响不同，每种故障所对应的齿根应变偏差与相应的时变啮合刚度有一定的相关性，所以可以根据内齿圈齿根应变偏差的形式判断不同内齿圈故障的类型。

(a) 齿面剥落

(b) 轮齿缺损

(c) 裂纹

对于内齿圈故障，当故障剧烈程度不同时，内齿圈齿根应变信号的表现与行星轮、太阳轮故障具有相同的规律，在此不再详述。

5 结 论

本文研究了行星齿轮箱典型故障对内齿圈齿根应变的影响，得到以下结论：

(1) 行星齿轮箱中太阳轮、行星轮、内齿圈的故障均可以引起内齿圈齿根应变的变化。

(2) 当行星齿轮箱出现故障时，内齿圈齿根应变信号中会出现与故障有关的频率成分：行星轮局部故障的频率为行星轮的自转频率，太阳轮局部故障的频率为太阳轮相对于行星架的旋转频率，内齿圈局部故障的频率为行星架的旋转频率。

(3) 不同类型的故障对内齿圈齿根应变信号的影响不同，每种故障下的内齿圈齿根应变的形式与相应的啮合刚度形式相关。

(4) 故障越剧烈，相应的内齿圈齿根应变偏差的能量水平越高。

通过以上结论可以发现，内齿圈齿根应变中包含有丰富的故障信息，是一种优质的故障特征载体信号，基于内齿圈齿根应变信号的行星齿轮箱故障诊断方法在理论上是可行的。

[1] PARKER R G, LIN J. Mesh phasing relationships in planetary and epicyclic gear[C]∥ASME 2003 design engineering technical conference and computers and information in engineering conference. Chicago: Journal of Mechanical Design, 2003.

[2] 雷亚国，汤伟，孔德同，等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J]. 机械工程学报, 2014, 50(17): 61-68.

LEI Yaguo, TANG Wei, KONG Detong, et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis[J]. Journal of Mechanical Engineering, 2014, 50(17): 61-68.

[3] INALPOLAT M, KAHRAMAN A. A theoretical and experimental investigation of modulation sidebands of planetary gear sets[J]. Journal of Sound and Vibration, 2009, 323(3/4/5): 677-696.

[4] FENG Z, ZUO M. Vibration signal models for fault diagnosis of planetary gearboxes[J]. Journal of Sound and Vibration, 2012, 331(22): 4919-4939.

[5] 冯志鹏，赵镭镭，褚福磊. 行星齿轮箱故障诊断的幅值解调分析方法[J]. 中国电机工程学报, 2013, 33(8): 107-111.

FENG Zhipeng, ZHAO Leilei, CHU Fulei. Amplitude demodulation analysis for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(8): 107-111.

[6] 冯志鹏，褚福磊. 行星齿轮箱故障诊断的频率解调分析方法[J]. 中国电机工程学报, 2013, 33(11): 112-117.

FENG Zhipeng, CHU Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(11): 112-117.

[7] 冯志鹏，范寅夕，LIANG Ming，等.行星齿轮箱故障诊断的非平稳振动信号分析方法[J]. 中国电机工程学报, 2013, 33(17): 105-110.

FENG Zhipeng, FAN Yinxi, LIANG Ming, et al. A nonstationary vibration signal analysis method for fault diagnosis of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(17): 105-110.

[8] 张小栋，谢思莹，牛杭，等. 光纤动态检测技术的研究与进展[J]. 振动、测试与诊断, 2015, 35(3):409-416.

ZHANG Xiaodong, XIE Siying, NIU Hang, et al. Research on dynamic measurement technology of fiber optic sensors and their development[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 409-416.

[9] NIU H, ZHANG X. Design on a bending stress measurement system of micro-gear with fiber Bragg grating[C]∥IEEE 10th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS). Xi’an:[s.n.], 2015.

[10] ZHAO X, NIU H, ZHANG X. Research on measurement for bending stress of gear with fiber Bragg grating (FBG) and optimization of FBG probe installation[C]∥IEEE 12th International conference on Ubiquitous Robots and Ambient Intelligence (URAI). Goyang:[s.n.], 2015.

[11] SANCHEZ M B, PEDRERO J I, PLEGUEZUELOS M. Critical stress and load conditions for bending calculations of involute spur and helical gears[J]. International Journal of Fatigue, 2013, 48(4):28-38.

[12] 靳广虎，朱如鹏，李政民卿，等. 齿宽系数对面齿轮齿根弯曲应力的影响[J]. 中南大学学报(自然科学版), 2011, 42(5):1303-1309.

JIN Guanghu, ZHU Rupeng, LI Zhengminqing, et al. Impact of coefficient of tooth width on bending stress of face gear[J]. Journal of Central South University (Natural Science), 2011, 42(5): 1303-1309.

[13] 孙智民，季林红，沈允文. 2K-H行星齿轮传动非线性动力学[J]. 清华大学学报(自然科学版), 2003, 43(5): 636-639.

SUN Zhimin, JI Linhong, SHEN Yunwen. Nonlinear dynamics of 2K-H planetary gear train[J]. Journal of Tsinghua University (Natural Science), 2003, 43(5): 636-639.

[14] 程哲，胡茑庆，冯占辉，等. 基于动力学仿真的行星轮系损伤检测方法[J]. 振动、测试与诊断, 2010, 30(4): 379-383.

CHENG Zhe, HU Niaoqing, FENG Zhanhui, et al. Detection of damage in planetary gear sets based on dynamical simulation[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4): 379-383.

[15] 李同杰，朱如鹏，鲍和云，等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报,2011,47(21): 76-83.

LI Tongjie, ZHU Rupeng, BAO Heyun, et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Engineering, 2011, 47(21): 76-83.

[16] Calculation of load capacity of spur and helical gears-part 3: calculation of tooth bending strength: ISO 6336-3—2006[S]. Switzerland: International Organization for Stand-ardization, 2006.

[17] SANCHEZ M B, PLEGUEZUELOS M, PEDRERO J I. Calculation of tooth bending strength and surface durability of internal spur gear drives[J]. Mechanism and Machine Theory, 2016, 95:102-113.

[18] CHAARI F, FAKHFAKH T, HADDAR M. Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking[J]. Journal of Failure Analysis & Prevention, 2006, 6(2):73-78.

[19] 万国志，訾艳阳，曹宏瑞，等. 时变啮合刚度算法修正与齿根裂纹动力学建模[J]. 机械工程学报，2013, 49(11): 153-160.

WAN Guozhi, ZI Yanyang, CAO Hongrui, et al. Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]. Journal of Mechanical Engineering, 2013, 49(11): 153-160.

[20] 杨军，张浬萍. 风电行星齿轮系统变载荷激励动力学模型及其响应特性[J]. 中国机械工程, 2013, 24(13): 1783-1788.

YANG Jun, ZHANG Liping. Varying load incentive dynamics model and response characteristic of planetary gear system of wind turbine[J]. China Mechanical Engineering, 2013, 24(13): 1783-178.

Action mechanism of planetary gearbox’s typical faults on tooth root strain of ring gear

NIU Hang2, ZHANG Xiaodong1，2, ZHAO Xindan2, HOU Chenggang2

(1. Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Planetary gearboxes have lots of advantages and are widely used in mechanical transmission systems of many fields. However, severe work conditions result in many failures of planetary gearboxes, so it is necessary to develop their fault diagnosis methods. Traditional fault diagnosis methods of planetary gearboxes based on vibration signals have limitations to identify their early and weak faults, so a new fault diagnosis method based on their ring gears’tooth root strain signals was proposed and the action mechanism of planetary gearbox’s typical faults on their tooth root strain of ring gear was discussed here. Firstly, the modeling method of the tooth root strain of ring gear was analyzed, and the model of the tooth root strain of ring gear was decomposed into the planetary wheelring gear meshing force model, the ring gear tooth form coefficient model and the load between teeth sharing coefficient model. Secondly, the planetary wheelring gear meshing force was calculated with the torsional model of planetary gearboxes, the ring gear tooth form coefficient was derived with the mechanics of materials, and the load between teeth sharing coefficeient of internal meshing was analyzed. Finally, the effects of the faults of planetary gearboxes on the meshing stiffness were studied, and the variation laws of tooth root strain of ring gear under typical faults were computed with the model of the toothroot strain of ring gear. The modeling simulation results showed that faults of different types, different positions and different intensities have different influences on the tooth root strain signals of ring gear and the proposed fault diagnosis method of planetary gearboxes based on tooth root strain is feasible theoretically.

planetary gearbox; ring gear; tooth root strain; vibration; fault diagnosis

国家自然科学基金(51675419)

2016-01-08 修改稿收到日期：2016-03-05

牛杭 男，博士，1991年生

侯成刚 男，博士，副教授，1968年生

TH132.41; TH17

A

10.13465/j.cnki.jvs.2017.09.037