变曲率FGM拱的面内自由振动分析

李万春， 滕兆春

(兰州理工大学 理学院，兰州 730050)

变曲率FGM拱的面内自由振动分析

李万春， 滕兆春

(兰州理工大学 理学院，兰州 730050)

基于Euler-Bernoulli曲梁理论，考虑材料沿拱厚度方向呈梯度分布时中性层的改变，将变曲率功能梯度材料(Functionally Graded Materials, FGM)拱在弧线方向离散成多个曲拱单元。视每个曲拱单元为半径一定的圆弧拱单元，根据Hamilton变分原理推导出FGM圆弧拱单元的面内自由振动方程，进而求得了单元传递矩阵。利用传递矩阵法(Transfer Matrix Method, TMM)推导出变曲率FGM拱的面内自由振动特征方程，求解两端固定边界条件下变曲率FGM拱面内自由振动的固有频率，并将得到结果与现有文献作了比较，证明TMM对求解该问题的有效性。分析了曲率变化系数和材料体积分数变化系数对变曲率FGM拱的面内自由振动频率的影响。

变曲率； FGM拱； 面内自由振动； 频率； 传递矩阵法

近年来，功能梯度材料(Functionally Graded Materials，FGM)以具有较高的力学性能越来越多的被应用和研究，其一般是由陶瓷和金属按指定的方向以一定的分布规律复合而成。对FGM性能的研究也成为结构设计及优化的重要内容，当然研究FGM结构的自由振动特性也有着十分重要的意义。Chakraborty等[1]基于一阶剪切变形理论研究了FGM直梁的自由振动问题，论证了FGM与均匀材料在动力问题上的差异。Goupee等[2]应用差分法通过对FGM材料组份的调整，进一步优化了FGM结构的自由振动特性。Malekzadeh等[3]根据层合理论和微分求积法研究了层合圆弧拱的面内自由振动，得出拱的几何参数和材料性能对自由振动结果的影响。Lü等[4]基于二维弹性理论、利用状态空间法研究了层合圆弧拱的固有频率与拱型几何参数和材料叠加顺序之间的关系。Tseng等[5]以Timoshenko曲梁为模型，在考虑剪切变形和转动惯量等因素的条件下对变曲率复合材料层合梁的自由振动进行了研究，求得了变曲率层合曲梁面内自由振动频率的精确解。Lim等[6]使用Fourier级数展开的方法分析了温度场中FGM圆弧拱的面内振动，讨论了功能梯度指数、温度和几何参数对振动频率的作用。Carlos等[7]结合FGM曲梁中性轴的变化推导出运动方程，通过幂级数法揭示了FGM曲梁的动力特性。Zeng等[8]采用二维弹性法对Mori-Tanaka和自洽两种FGM模型的拱进行了分析，评估功能梯度指数和拱型几何参数在两种模型中所得的不同自由振动频率。Ugurcan[9]通过梁理论方法，考虑轴向变形、剪切变形、转动惯量以及材料特性受温度的影响等因素，给出了热环境中FGM圆弧梁的面内自由振动规律。

本文基于Euler-Bernoulli曲梁理论，考虑材料沿拱厚度方向呈梯度分布时中性层的改变，将变曲率FGM拱沿弧线方向离散成多个曲拱单元。对每个曲拱单元，将其视为半径一定的圆弧拱单元，根据Hamilton变分原理[10]推出FGM圆弧拱单元做面内自由振动时径向位移所满足的微分方程，用传递矩阵法(Transfer Matrix Method，TMM)[11]建立变曲率FGM拱的面内自由振动特征方程，相对于上述研究方法，TMM能够通过小型矩阵解决大型结构的动力分析，并且还兼具求解思路清晰、计算过程简单等优势。最后通过算例计算总张角固定、曲率沿张角呈线性变化的变曲率FGM拱的面内自由振动频率，分析了曲率变化系数和材料体积分数变化系数对自由振动频率的影响。同时，将变曲率FGM拱退化到均匀材料圆弧拱，并和文献[12]的有限元计算结果作了对比，结果完全吻合，说明应用TMM研究变曲率FGM拱的面内自由振动问题有效。

1 计算模型及控制方程

1.1 计算模型的建立

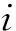
(a)(b)

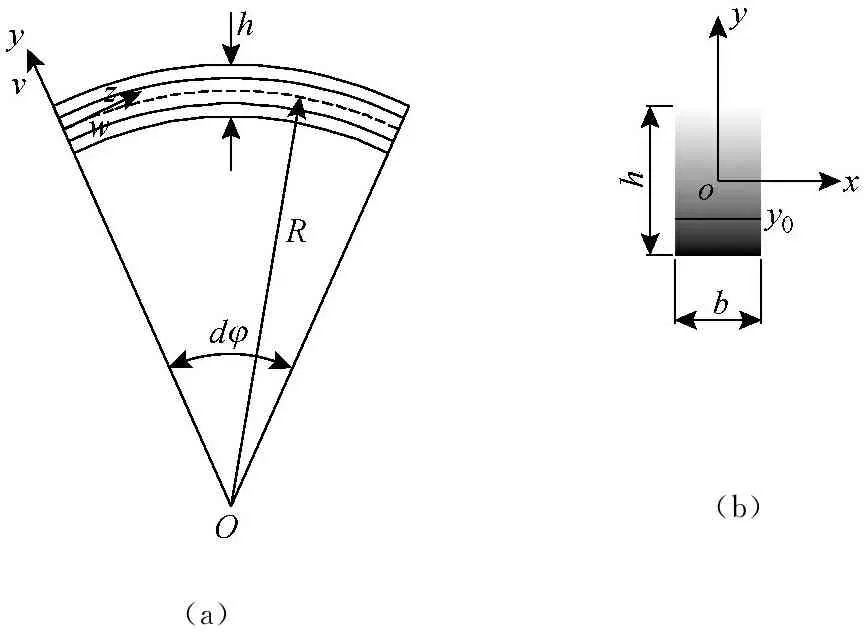
图1 FGM圆弧拱的曲线坐标系

Fig.1 The curvilinear coordinate system of a FGM circular arch

图1中R为拱单元几何中面的曲率半径，dφ为拱单元所对应的张角，h，b为拱单元截面的几何尺寸，v，w为拱单元做面内自由振动时的径向、周向位移，y0为拱单元横截面中性层的位置。

1.2 曲率及材料梯度变化规律

考虑曲率沿张角呈线性变化，FGM由陶瓷和金属复合而成，其中金属相的体积分数沿拱厚度方向呈幂律分布，即

κ=κ0+k·φ

(1)

(2)

式中：κ、κ0、k和φ分别为拱轴线任一点处的曲率、初曲率、曲率变化系数和拱轴线任一点的张角，且k的单位为(rad·m)-1；p为金属相体积分数变化系数。

1.3 横截面中性层位置的确定

对沿拱厚度方向呈幂律分布的FGM横截面，其中性层[13]随梯度指数的变化而变化，如图1所示，若中性层为y=y0，根据平面假设，拱的应变为

ε=(y0-y)/R*

(3)

式中,R*=R+y0为中性层的曲率半径。根据线弹性材料的本构关系，有

陶瓷的应力

σc=Ecε

(4)

金属的应力

σm=Emε

(5)

式中,Ec、Em分别为陶瓷和金属的弹性模量。

由复合材料力学得，拱上任一点的总应力为

σ=[1-f(y)]σc+f(y)σm

(6)

由此可得平衡方程

(7)

结合式(3)～式(6)，由式(7)可得中性层的位置

(8)

1.4 控制方程的推导

如图1所示FGM圆弧拱单元，对沿拱厚度呈式(2)分布的FGM拱单元，其材料性质有如下规律[14]

(9)

(10)

式中，ρc、ρm分别为陶瓷和金属的质量密度。取径向坐标为y，厚度为dy的横截面，将其视为均匀材料的圆弧拱层，设其为圆弧拱的第K层，对均匀材料圆弧拱，其两端弯矩和轴力有如下关系[15]

(11)

(12)

根据Hamilton变分原理，在时间区段[t1,t2]上有

(17)

将式(15)和式(16)代入式(17)中，而后对各项进行分部积分计算，其中有位移在时刻t1、t2上的变分为0，即

(18)

并结合边界条件，有

简支边界

(19)

(20)

固定边界

(21)

(22)

这样，对式(17)进行化简，经整理可得简支或固定边界条件下FGM圆弧拱的面内自由振动控制方程

(23)

(24)

对式(23) 进行弧长s的一阶微分，式(24) 两边同时除以R*，而后两式相加，经化简可得

(25)

考虑FGM圆弧拱轴向不可伸长，即

(26)

故式(25)进一步得到简化，得

(27)

在忽略切向惯性力的影响时，有

(28)

根据文献[12]得到拱轴不可压缩，忽略剪力、转动惯量和切向惯性力影响时FGM圆弧拱做面内自由振动时径向位移满足的微分方程，即控制方程

(29)

又根据圆弧拱ds=R*dφ，故式(29)又可化为

(30)

2 传递矩阵及特征方程

2.1 单元传递矩阵

式中,U、V、θ、M、Q、N分别为对应节点处的轴向位移、径向位移、转角、弯矩、剪力和轴力。

根据控制方程(30)，假设该拱做简谐振动，有

v=Vcosωt

(33)

将式(33)代入式(30)中，得

(34)

式(34)中

(35)

若设式(35)中

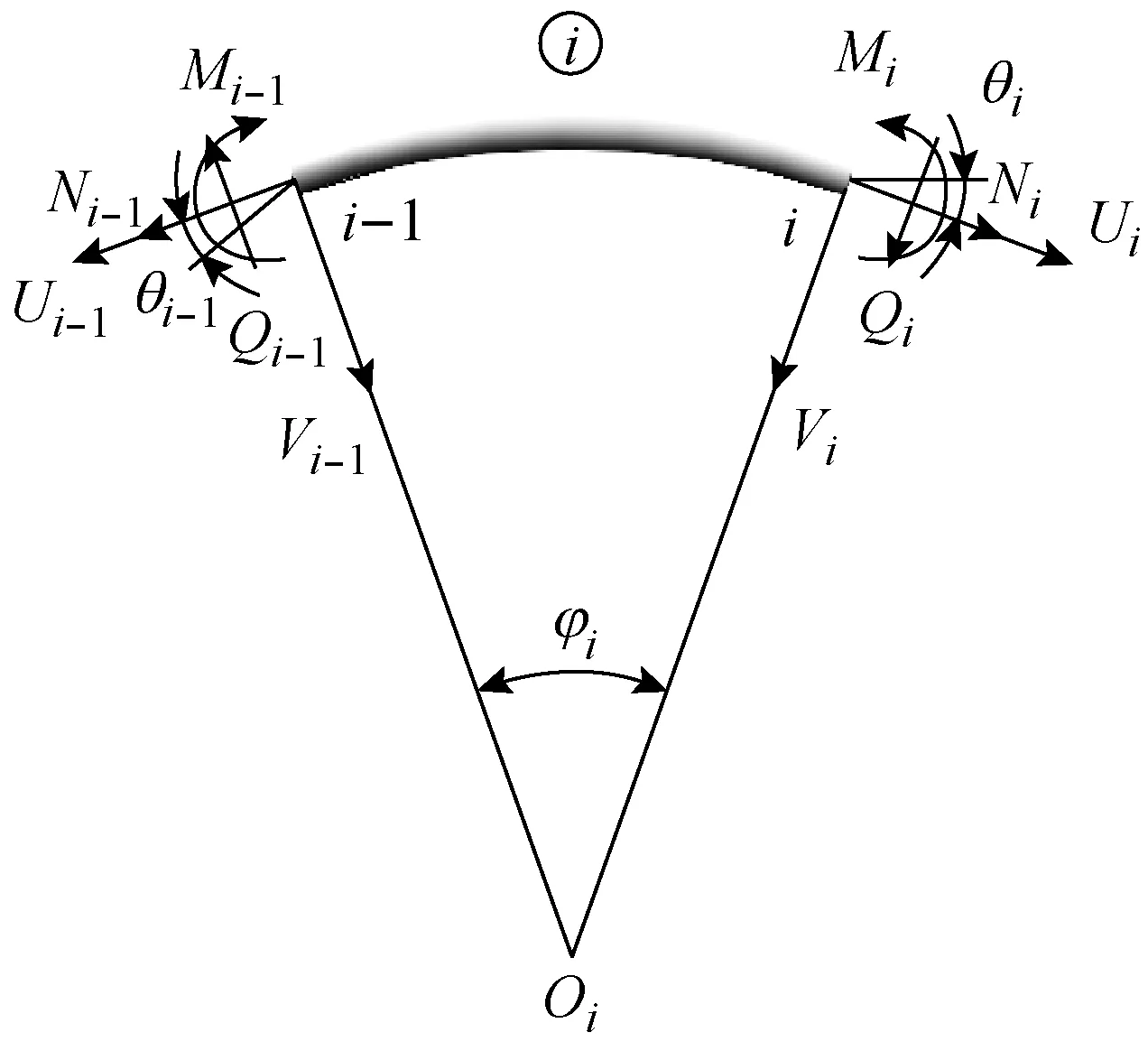
图2 单元○i状态模量分析

(36)

求解式(34)，有

(1) 当λ≥1时，令

(37)

则式(34)的解为

V=C1+C2ch(βφ)+C3sh(βφ)+C4cos(αφ)+C5sin(αφ)

(38)

由式(38)可进一步求得U、θ、M、Q和N分别为

(39)

(40)

(41)

(42)

(43)

(2) 当0<λ<1时，令

(44)

同理可解得式(34)，进一步得出U、θ、M、Q和N分别为

V=C1+C2cos(αφ)+C3sin(αφ)+C4cos(βφ)+C5sin(βφ)

(45)

(46)

(47)

(48)

(49)

(50)

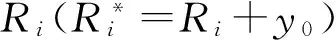
Si-1=Ti-1C

(51)

Si=TiC

(52)

式中,C=[C1,C2,C3,C4,C5,C6]T。由此得

(53)

将式(53)代入式(52)中，得

(54)

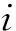
(55)

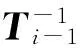
(56)

对节点i处，有φ=φi，同理将其代入式(38)～式(43)中， 并将这6组方程写成矩阵形式，可得Ti

(57)

由式(55)即可以得出λ≥1时的单元传递矩阵Hi。同理当0<λ<1时有

(58)

(59)

由式(55)又得出0<λ<1时的单元传递矩阵Hi。

2.2 总传递矩阵

Ri=Rφi/2

(60)

根据各相邻FGM拱单元间的连续性，即任一单元左端的状态模量是与其相邻上一单元右侧的状态模量，任一单元右侧的状态模量是与其相邻下一单元左侧的状态模量，若设变曲率FGM拱单元始端的状态模量为S0，则任一端的状态模量Si与始端状态模量S0有如下关系

Si=Hi·Hi-1·Hi-2…H2·H1·S0

(61)

整个变曲率FGM拱划分为n段，则末端状态模量与始端状态模量之间的关系有

Sn=Hn·Hn-1…Hi…H2·H1·H0=H·S0

(62)

式中,H为变曲率FGM拱的总传递矩阵，且

H=Hn·Hn-1…Hi…H2·H1·H0

(63)

求得了各FGM圆弧拱单元的单元传递矩阵，根据式(63)即可求得变曲率FGM拱的总传递矩阵。

2.3 特征方程

对于拱型结构的边界条件，在式(31)、式(32)中所设状态模量均能找到3个元素为0，这样，结合线性代数[16]中关于齐次线性方程组有非零解的充要条件的相关知识，在H中的对应元素所构成的行列式要等于0，即

Δ(α,β,λ)=0

(64)

将式(37)或式(44)代入式(64)中，结合式(35)得变曲率FGM拱面内自由振动的特征方程

Δ(ω)=0

(65)

求解式(65)，即可求得变曲率FGM拱的面内自由振动的频率和相应的振型。

3 算例分析

曲率按式(1)、材料按式(2)连续变化的矩形截面变曲率FGM拱，其张角φ=5π/9rad，截面尺寸b×h=0.3 m2×0.8 m2，拱的左端点处的半径、即初始半径R0=60 m，约束为两端固定。材料相关物理参数如表1所示。

表1 陶瓷和金属的物理参数

当取曲率变化系数k=0、金属相体积分数变化系数p→+∞时，变曲率FGM拱便退化到各向同性均匀材料金属圆弧拱。

表2给出了在曲率固定，即κ=κ0=1/60的金属圆弧拱在分段数为20时的前五阶面内自由振动频率ω的计算结果，并和文献[12]的有限元计算结果作了比较。由表2可以看出，即使在分段数较少的情况下(这里n=20)，本文得出的结果与文献[12]的有限元计算结果比较吻合，相对误差在0.4%以内，显示了利用TMM解决此类问题的适用性和精确性。

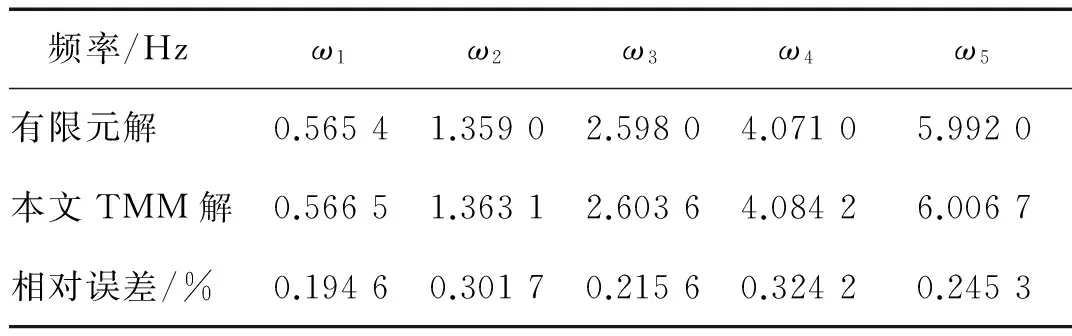
表2 金属圆弧拱的面内自由振动频率ω

变曲率FGM拱的前四阶面内自由振动频率ω与曲率变化系数k对应的关系曲线如图3，其中曲率变化系数k∈[-1/6 000,1/6 000]，p∈[0,+∞),n=20。由图3(a)～图3(d)看出，在体积分数变化系数p一定时，变曲率FGM拱的前四阶面内自由振动频率ω与曲率变化系数k基本都呈线性变化关系，ω值随着k值的增大而增大，且p值越小，这种线性比例关系越明显。

变曲率FGM拱的前四阶面内自由振动频率ω随材料体积分数变化系数p对应的关系曲线如图4，其中p∈[0,100]。由图4(a)～图4(d)可以看出，在曲率变化系数k一定时，变曲率FGM拱的前四阶面内自由振动频率都随体积分数变化系数p的增大而减小，且在p∈(0～10)时递减最为剧烈。当p足够大时，随p继续增大，ω的值趋于稳定，也反映了变曲率FGM拱的面内自由振动频率是从陶瓷材料向金属材料过渡的特点。

4 结 论

本文基于Euler-Bernoulli曲梁理论，考虑材料沿拱厚度方向呈梯度分布时中性层的改变，利用TMM研究变曲率FGM拱的面内自由振动问题。首先将变曲率FGM拱沿弧线方向离散成多个FGM曲拱单元，视每个FGM曲拱单元为半径一定的FGM圆弧拱单元，根据变分原理推导出FGM圆弧拱单元的面内自由振动方程，进而用TMM导出了FGM圆弧拱单元两端状态模量的单元传递矩阵和变曲率FGM拱的总传递矩阵，最后结合边界条件及线性代数中关于齐次线性方程组有非零解的充要条件的相关知识，求得变曲率FGM拱面内自由振动的各阶频率。将所得到的解退化到各向同性均匀材料圆弧拱情况下的结果，与已有的有限元解一致。结果表明本文所建立的拱结构力学模型可靠，理论公式推导正确。由适用条件和精度要求可见，本文所采用的方法是适用于解决变曲率FGM拱的面内自由振动问题的，是分析变曲率FGM拱面内自由振动特性的一种行之有效的方法。

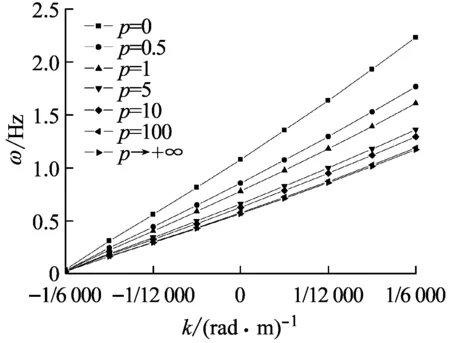
(a) 一阶频率

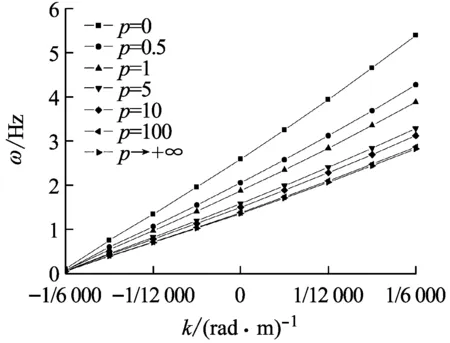
(b) 二阶频率

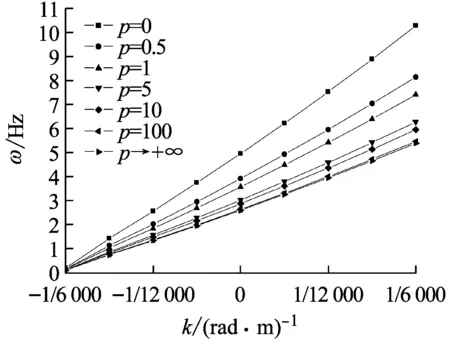
(c) 三阶频率

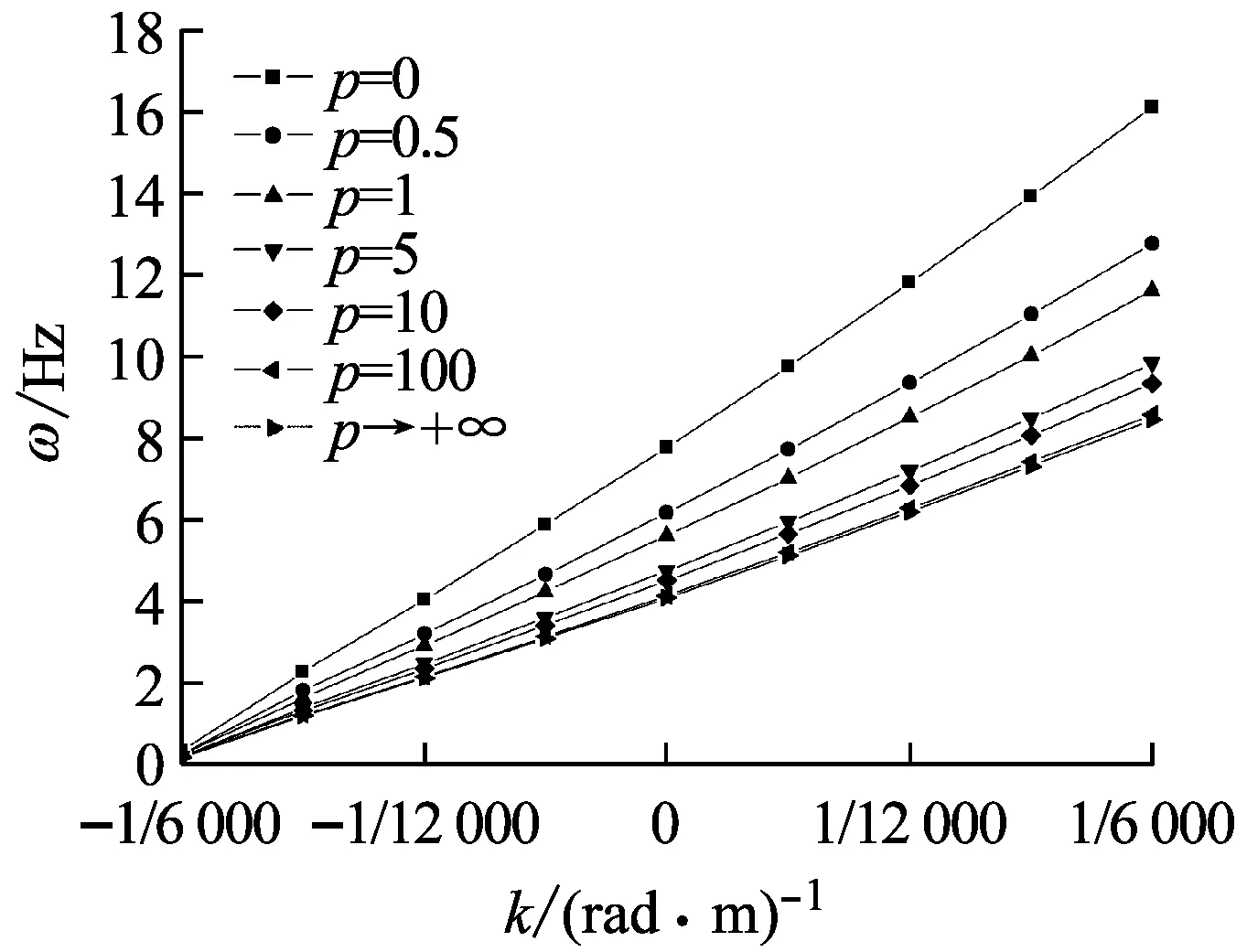
(d) 四阶频率

Fig.3 Dependence of the curvature coefficientkof variation on the first four in-plane free vibration frequencies of FGM arches variable curvature

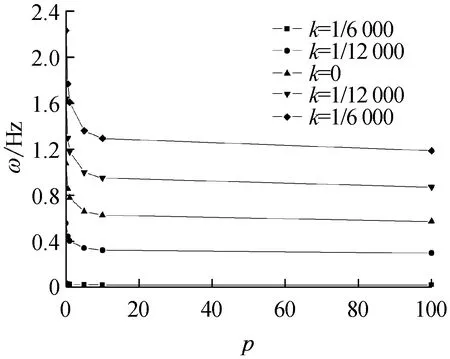
(a) 一阶频率

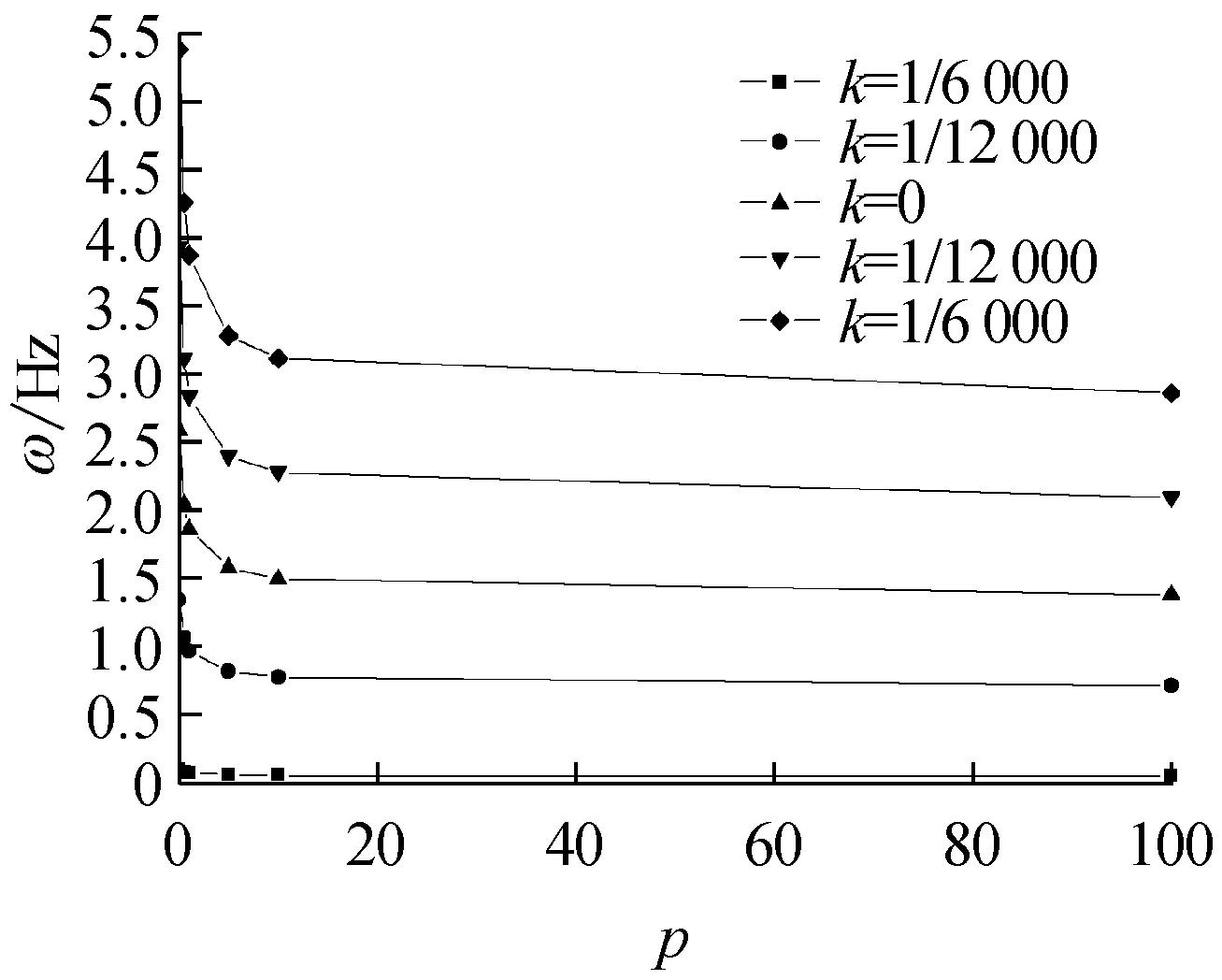
(b) 二阶频率

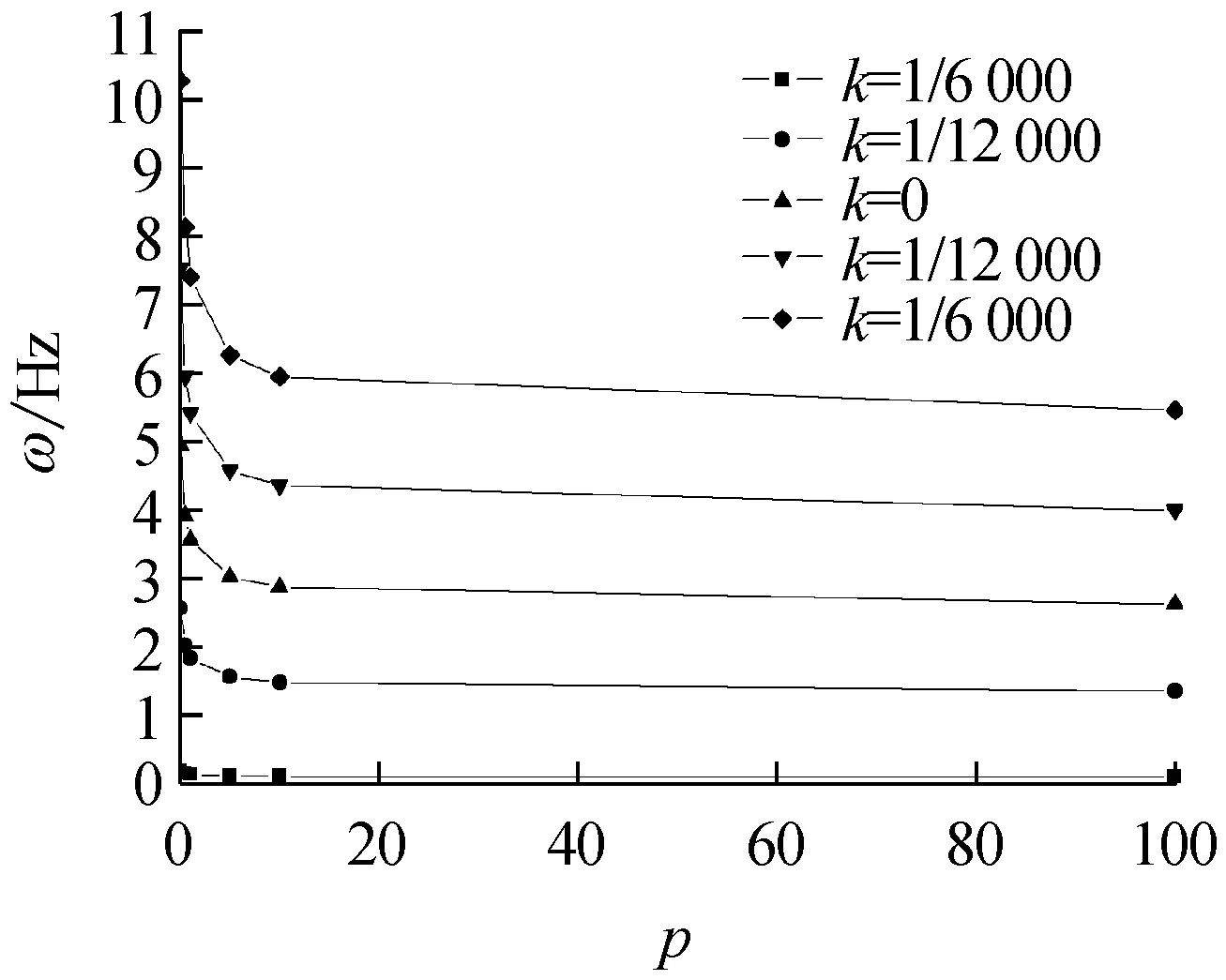
(c) 三阶频率

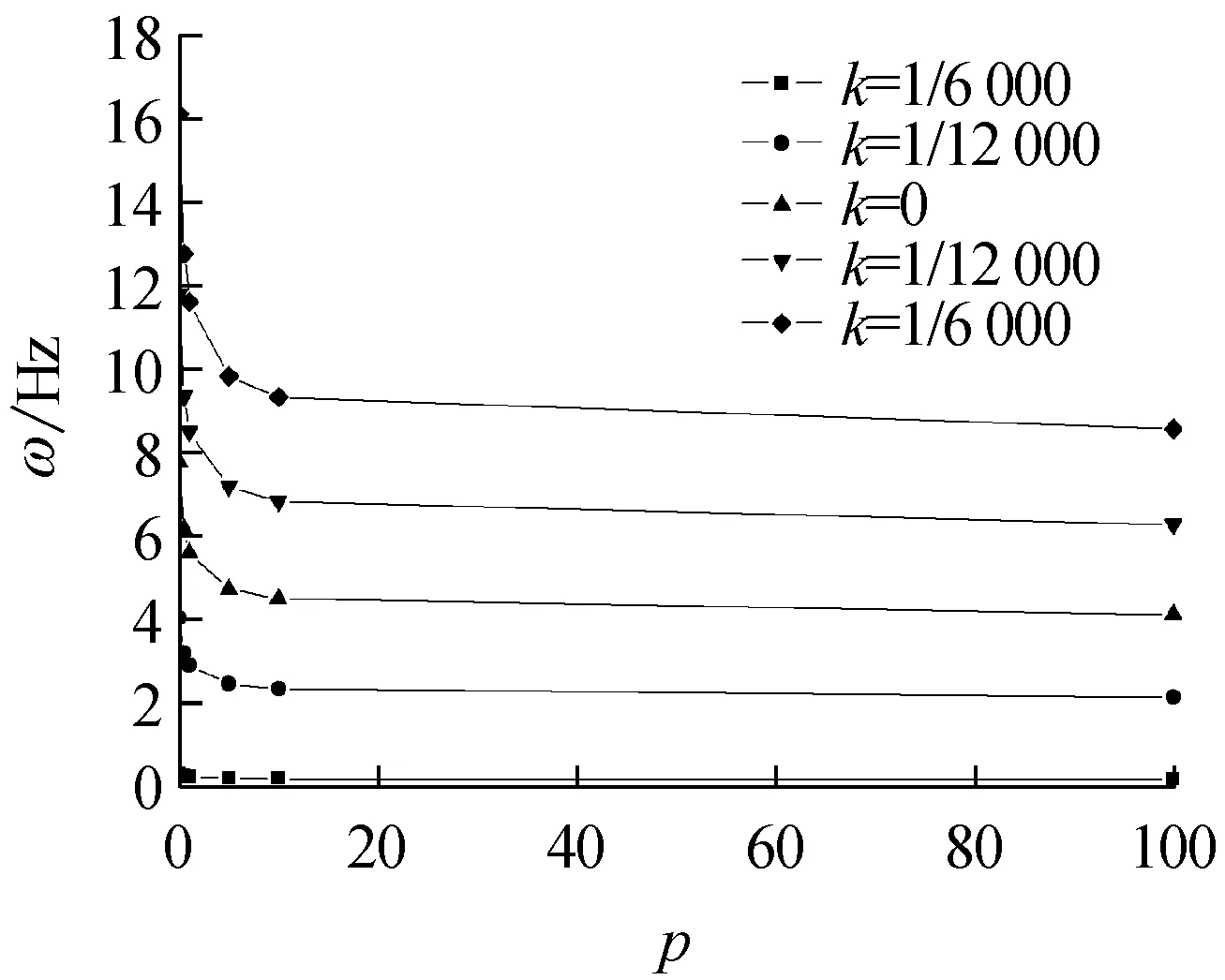
(d) 四阶频率

Fig.4 Dependence of material volume fractionpof variation on the first four in-plane free vibration frequencies of FGM arches with variable curvature

[1] CHAKRABORTY A, GOPALAKRISHNAN S, REDDY J N. A new beam finite element for the analysis of functionally graded materials[J]. International Journal of Mechanical Sciences， 2003, 45(3):519-539.

[2] GOUPEE A J, VEL S S. Optimization of natural frequencies of bidirectional functionally graded beams[J]. Structural and Multidisciplinary Optimization, 2006, 32(6):473-484.

[3] MALEKZADEH P, SETOODEH A R, BRRMSHOURI E. A hybrid layerwise and differential quadrature method for in-plane free vibration of laminated thick circular arches[J]. Journal of Sound and Vibration, 2008, 315(1/2): 212-225.

[4] LÜ Q, LÜ C F. Exact two-dimensional solutions for in-plane natural frequencies of laminated circular arches[J]. Journal of Sound and Vibration, 2008, 318(4/5): 982-990.

[5] TSENG Y P，HUANG C S，KAO M S. In-plane vibration of laminated curved beams with variable curvature by dynamic stiffness analysis[J]. Composite Structures, 2000, 50(2): 103-114.

[6] LIM C W, YANG Q, LÜ C F. Two-dimensional elasticity solutions for temperatire-dependent in-plane vibration of FGM circular arches[J]. Composite Structures, 2009, 90(3): 323-329.

[7] CARLOS P F, MARCELO T P. The dynamics of thick curved beams constructed with functionally graded materials[J]. Mechanics Research Communications, 2010,37(6):565-570.

[8] ZENG Q C, LIM C W, LÜ C F, et al. Asymptotic two-dimensional elasticity approach for free vibration of FGM circular arches[J]. Mechanics of Advanced Materials and Structures, 2012, 19(1/2/3):29-38.

[9] UGURCAN E. In-plane free vibrations of circular beams made of functionally graded material in thermal environment: Beam theory approach[J]. Composite Structures, 2015, 122:217-228.

[10] 胡海昌. 弹性力学的变分原理及其应用[M]. 北京: 科学出版社, 1982.

[11] 向天宇, 郑建军. 变截面圆拱的自由振动[J]. 振动与冲击, 2000, 19(2):59-63.

XIANG Tianyu, ZHENG Jianjun. Free vibration of circular arches with variable cross-section[J]. Journal of Vibration and Shock, 2000, 19(2):59-63.

[12] ZHAO Y Y, KANG H J. In-plane free vibration analysis of cable-arch structure[J]. Journal of Sound and Vibration, 2008, 312(3): 363-379.

[13] 孙训方, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 1982.

[14] LI S R, SU H D, CHENG C J. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment[J]. Applied Mathematics and Mechanics (English Edition), 2009, 30(8): 969-982.

[15] VIOLA E, ARTIOLI M, DILENA M. Analytical and differential quadrature results for vibration analysis of damaged circular arches[J]. Journal of Sound and Vibration, 2005, 288(4/5): 887-906.

[16] 同济大学数学教研室. 线性代数[M]. 北京: 高等教育出版社, 1999.

In-plane free vibration analysis of FGM arches with variable curvature

LI Wanchun， TENG Zhaochun

(School of Science, Lanzhou University of Technology, Lanzhou 730050, China)

Based on the theory of Euler-Bernoulli curved beam, the shifting of neutral layer was considered when materials were gradually distributed trapezoidally along the arch thickness, and functionally graded material (FGM) arches with variable curvature were discretized into a number of curved arch elements along the arc direction. Every curved arch element was considered as a circular arch element with a constant radius, according to Hamilton variational principle, the in-plane free vibration equation of a FGM circular arch element was derived, then the element transfer matrix was deduced. Furthmore, using TMM, the in-plane free vibration characteristic equation of the FGM arch with variable curvature was derived, the in-plane free vibration natural frequencies of the FGM arch with variable curvature under two-clamped end boundary condition were solved, the results were compared with those previously reported. It was shown that TMM is effective to solve this problem. The influences of curvature varying coefficient and material volumn fraction varying coefficient on the in-plane free vibration frequencies of the FGM arch with variable curvature were analyzed.

variable curvature; functionally graded materials arches; in-plane free vibration; frequency; transfer matrix method

国家自然科学基金(11662008)；甘肃省自然科学基金(148RJZA017)

2016-01-08 修改稿收到日期：2016-03-16

李万春 男，硕士生，1984年生

滕兆春 男，副教授，1969年生

O343

A

10.13465/j.cnki.jvs.2017.09.030