非平稳随机地震响应约束下的桁架结构形状与拓扑优化

李雪平， 李栋泓， 魏 鹏， 苏 成

(华南理工大学 土木与交通学院 亚热带建筑科学国家重点实验室，广州 510640)

非平稳随机地震响应约束下的桁架结构形状与拓扑优化

李雪平， 李栋泓， 魏 鹏， 苏 成

(华南理工大学 土木与交通学院 亚热带建筑科学国家重点实验室，广州 510640)

基于时域显式方法，针对桁架结构在非平稳随机地震作用下的动力优化问题推导了非平稳随机响应对设计参数的灵敏度，并结合移动渐进线法对桁架结构的截面积及节点坐标进行优化。建立了以体积为目标函数，以水平向及竖向地震作用下位移方差为约束条件的优化模型。通过数值算例说明桁架在非平稳随机地震作用下进行动力优化的可行性以及该方法的有效性。

桁架；非平稳；拓扑优化；时域显式法

建筑结构常常受到随机荷载的作用，如地震、风和海浪等。结构在受到随机荷载作用时，大体上有两类方法可以抑制或减少结构的振动。一是传统的振动控制方法，包括主动控制、被动控制、半主动控制等。二是通过对结构的尺寸、形状和拓扑进行优化以改善结构动力特性的方法[1]。为了避免结构动力响应过大导致的结构失稳或疲劳损坏，以结构某些关键部位的动力响应为约束条件或目标函数进行的动力特性优化近年来引起了越来越多的关注[2]。

结构的动力响应一般是结构设计参数的隐式函数，具有高非线性与复杂性等特征，这就导致动力响应求解、灵敏度分析比较困难。对此问题，很多学者已经开展了大量的研究工作，Rong等采用模态叠加法和序列二次规划法(Sequential Quadratic Programming，SQP)对结构受白噪声激励下的动力响应进行优化，以使结构的质量达到最轻的目标。Zhang等[3]考虑静荷载对结构刚度的影响，采用模态叠加法对结构受平稳激励下的多种材料布局进行了拓扑优化。Li等[4]采用移动渐近线法(Method of Moving Asymptotes，MMA)对区间参数结构的动力可靠度进行优化，其动力响应及灵敏度求解采用等效静力法( Equivalent Static Load，ESL)进行处理。潘晋等[5]采用遗传算法对桁架结构受脉冲激励下的响应进行拓扑优化，计算效率相对较低。Jog[6]针对结构受周期性荷载作用的问题，分别以响应和动力柔顺度最小化为目标函数对连续体结构进行拓扑优化。Hajirasouliha等[7]针对类桁架结构在确定性地震荷载作用下的响应，考虑了桁架结构的非线性与受压杆件的屈曲效应，对桁架结构的截面进行了拓扑优化。Rong[8]采用模态叠加法求解结构在白噪声激励下的响应并推导其动力响应的灵敏度，结合进化优化算法(Evolutionary Structure Optimization，ESO)研究了连续体的动力拓扑优化。Gomes[9]采用粒子群优化算法(Particle Swarm Optimization，PSO)对桁架结构在频率约束下的节点坐标以及杆件截面积进行了优化。Ma等[10]以结构的动力可靠度为约束条件，体积为目标函数，对桁架结构在平稳激励作用下的截面积以及节点位置进行了优化。Miguel等[11]采用改进的智能优化算法对桁架结构在频率约束下的节点及杆件截面积进行拓扑优化。房占鹏等[12]针对指定频带简谐激励下对约束阻尼结构进行拓扑优化。通过查阅国内外文献可以发现基于响应的动力拓扑优化主要集中在确定性荷载或平稳激励作用下，而对于结构受非平稳随机激励下的动力拓扑优化文献还相对较少，而且非平稳响应及灵敏度求解相对平稳问题求解更为复杂。

近年来由苏成等[13-14]提出的时域显式法可显式表达出结构的动力响应，进而可以高效求解结构在非平稳激励下的动力响应。陈太聪等[15]基于精细积分格式提出了非平稳随机响应灵敏度的时域显式法。本文基于Newmark-β的积分格式推导了非平稳随机响应灵敏度的时域显式法，通过对比发现，当结构主频率处于荷载主频率范围时，在同等精度条件下，基于精细积分的时域显式法效率更高。而通常情况下，为了减少外载荷产生的振动，一般结构主频率会设计的偏离荷载主频范围，这样基于Newmark-β的积分格式的时域显式法效率更高。因此本文采用基于Newmark-β的积分格式的时域显式法求解响应对设计参数的灵敏度并结合全局收敛的移动渐进线法(Globally Convergent Method of Moving Asymptotes，GCMMA)[16]研究了非平稳随机地震作用下桁架结构的形状与拓扑优化问题，通过两个算例来说明非平稳随机响应动力优化的可行性以及该方法的有效性。

1 非平稳随机动力响应及灵敏度分析

考虑某n个自由度的线性系统，其在地震作用下的动力学方程为

(1)

(i=1,2,…,l)

(2)

(3)

式中：I为单位矩阵；积分参数γ和β可分别取0.5和0.25，以保证数值积分的稳定性。当系统的初始状态V0等于零向量时，并且记N=TQ2+Q1，由递推关系式可以推导出响应Vi的时域显式表达式

(4)

其中，

(5)

式中，Ai,Ai-1,…,A1只与结构参数有关，反映结构参数对动力响应的影响。式(4)可以进一步表示为

(6)

其中，

(7)

最后响应可以表示为与结构参数有关的系数向量和与荷载有关的向量相乘的显式表达式，有利于结构响应统计特性的求解。由于在结构随机振动分析中，通常只对结构某些关键部位响应感兴趣，所以并不需要求解所有的响应向量，从而可以节省大量的计算量。由式(6)可知，在时刻ti某一关键部位的响应vi可写为

(8)

式中，φ为关键部位结构响应的定位行向量，其元素由0和1组成。

基于以上动力响应时域显式表达的基本思路，可推导出动力响应灵敏度的时域显式求解列式。设θ代表结构的某个设计参数，则对动力学方程式(1)两端求偏导，可得

(9)

其中，

(10)

对比观察式(1)和式(9)可见，两方程仅荷载项不同，因此也可采用Newmark-β积分格式推导其关于灵敏度的时域表达式

(11)

其中，

(12)

根据随机响应的方差灵敏度的一般计算公式[19]

(13)

将式(6)和式(11)代入，最终整理可得第i时刻结构响应vi的方差对设计参数θ的灵敏度的计算表达式为

(14)

其中，

(15)

以平面桁架结构的M、C、K为例，对截面积及节点坐标的灵敏度可表示如下。

单元刚度对截面积(θ=A)的导数

(16)

其中，

(17)

单元质量对截面积(θ=A)的导数

(18)

单元刚度对节点x坐标(θ=x1)的导数

(19)

其中，

n=Δx*(3*Δx2-2*l2)

m=3*Δx*Δy2

k=Δy*(3*Δx2-l2)

(20)

单元质量对节点x坐标(θ=x1)的导数

(21)

单元刚度对节点y坐标(θ=y1)的导数

(22)

其中，

p=3*Δy*Δx2

q=Δy*(3*Δy2-2*l2)

r=Δx*(3*Δy2-l2)

(23)

单元质量对节点y坐标(θ=y1)的导数

(24)

单元阻尼对设计变量的导数

(25)

通过以上分析可得单元刚度矩阵、质量矩阵以及阻尼矩阵对设计参数的灵敏度，然后再组装成总刚度矩阵、质量矩阵以及阻尼矩阵，最后由式(14)即可求得平面桁架位移方差对各设计参数的灵敏度。该推导过程可以直接推广到空间桁架结构的灵敏度分析，由于篇幅原因，不在此赘述。

2 桁架结构在非平稳地震激励下的形状与拓扑优化

A0≤Aj≤A(j=1,2,…,m)

xk≥0,yk≥0 (k=1,2,…,p)

(26)

图1 优化流程图

3 数值算例

算例1 36杆平面桁架优化

考虑如图2所示平面桁架结构，同时受水平和竖向随机地震加速度F1(t) m/s2，F2(t) m/s2的作用，单元各杆件的弹性模量E=210×109Pa，杆件尺寸如图中所示。杆件的密度为ρ=7 800 kg/m3,杆件质量堆积到杆两端。此外，A、B、C、D节点处另有附加质量MA=MB=MC=MD=25 000 kg。阻尼采用Rayleigh阻尼，其中的阻尼系数α=0.2、β=0.001。Fi(t)(i=1,2)取为均匀调制非平稳随机过程，即Fi(t)=g(t)fi(t)。其中，调制函数g(t)选取三段式包络函数如下

图2 36杆平面桁架结构初始模型

(27)

式中：t1=3 s；t2=6 s；t3=15 s；c=0.157 2。f(t) 为0均值高斯平稳随机过程，其功率谱密度函数取为Kanai-Tajimi过滤白噪声谱，即

(28)

式中：ωg=14 rad/s(地基土的卓越频率)；ζg=0.6(地基土的阻尼比)；S0=0.07 m2/s3(谱强度因子，竖向地震取为水平地震强度因子的1/2)。

该算例以结构体积最小化为目标，计算时间步长Δt=0.02 s，考虑以下三种情况：

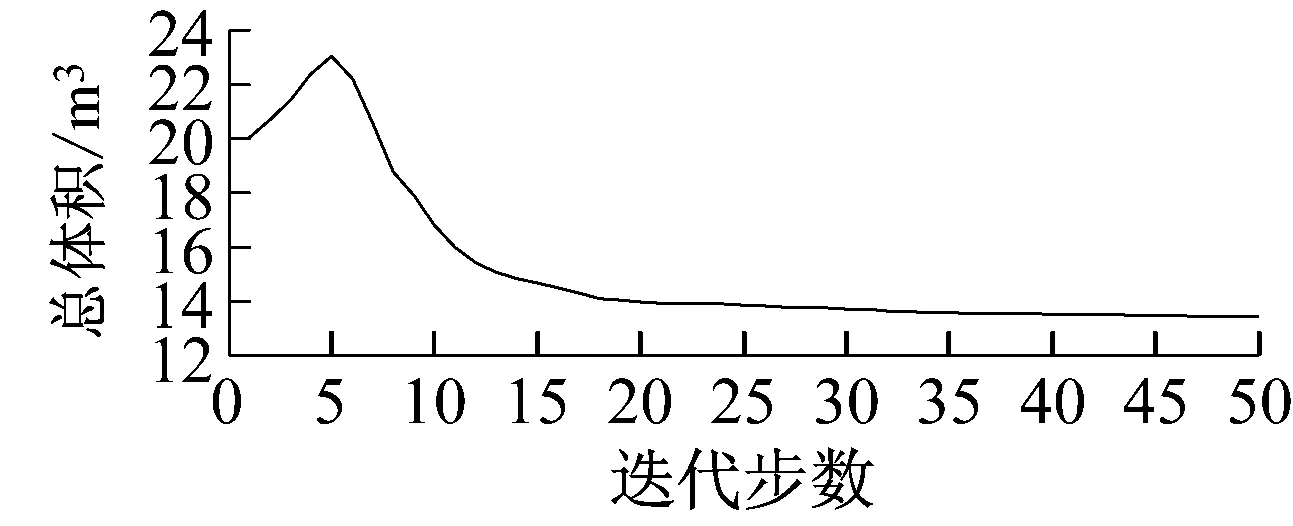
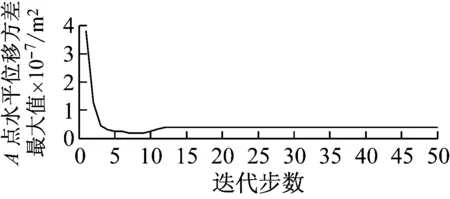
优化后的结构如图3所示；优化目标和约束条件的迭代曲线如图4所示；优化前后约束点处水平位移方差最大值、竖向位移方差最大值及总体积见表1。

图3 桁架结构截面优化结果

(a) 总体积收敛曲线

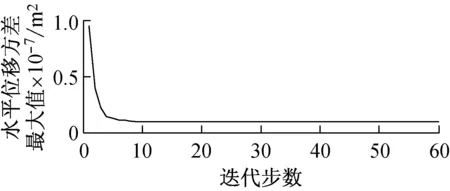
(b) A点水平位移方差最大值收敛曲线

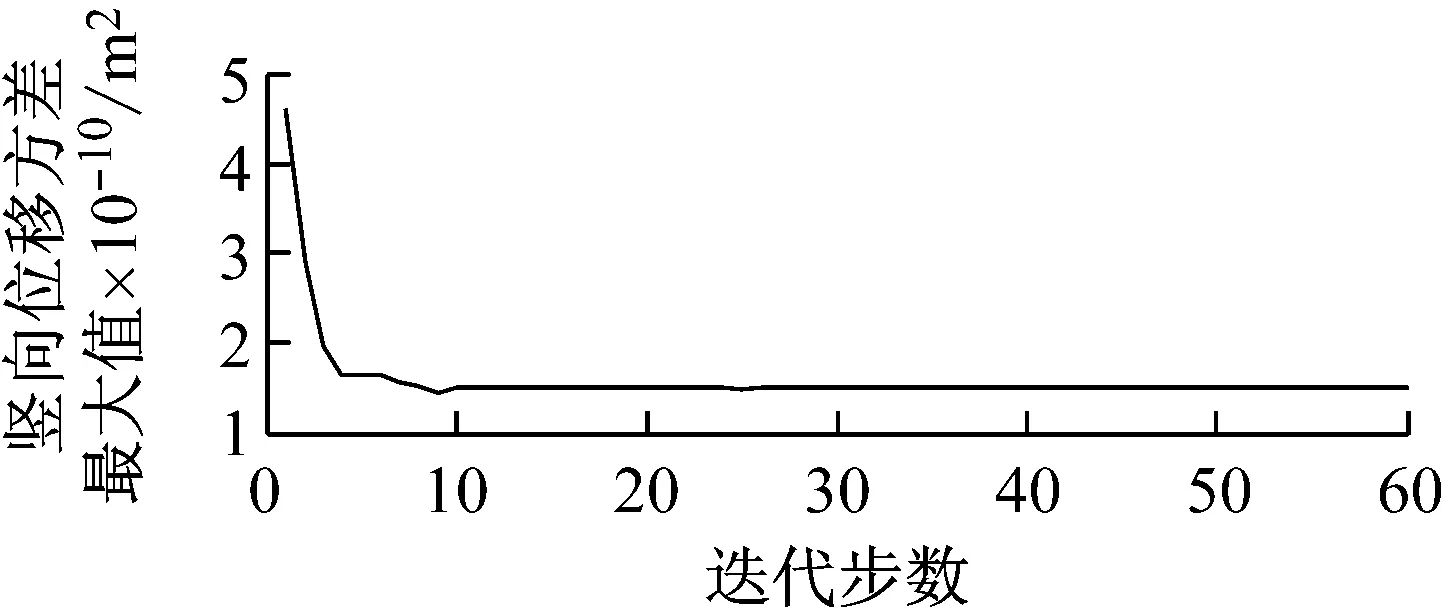
(c) A点竖向位移方差最大值收敛曲线

Fig.4 Convergence curve of structure’s total volume and the maximum horizontal and vertical displacement variance of pointAin the process of optimization

优化后的结构如图5所示，优化目标和约束条件的迭代曲线如图6所示，优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积见表2。

表1 优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积

Fig.1 Maximum horizontal and vertical displacement variance at constraint point before and after optimization and structure’s total volume

σ2AVmaxσ2AHmax总体积优化前9.5×10-84.6×10-1040优化后1.0×10-81.5×10-1035.52

图5 桁架结构截面积与节点x坐标优化结果

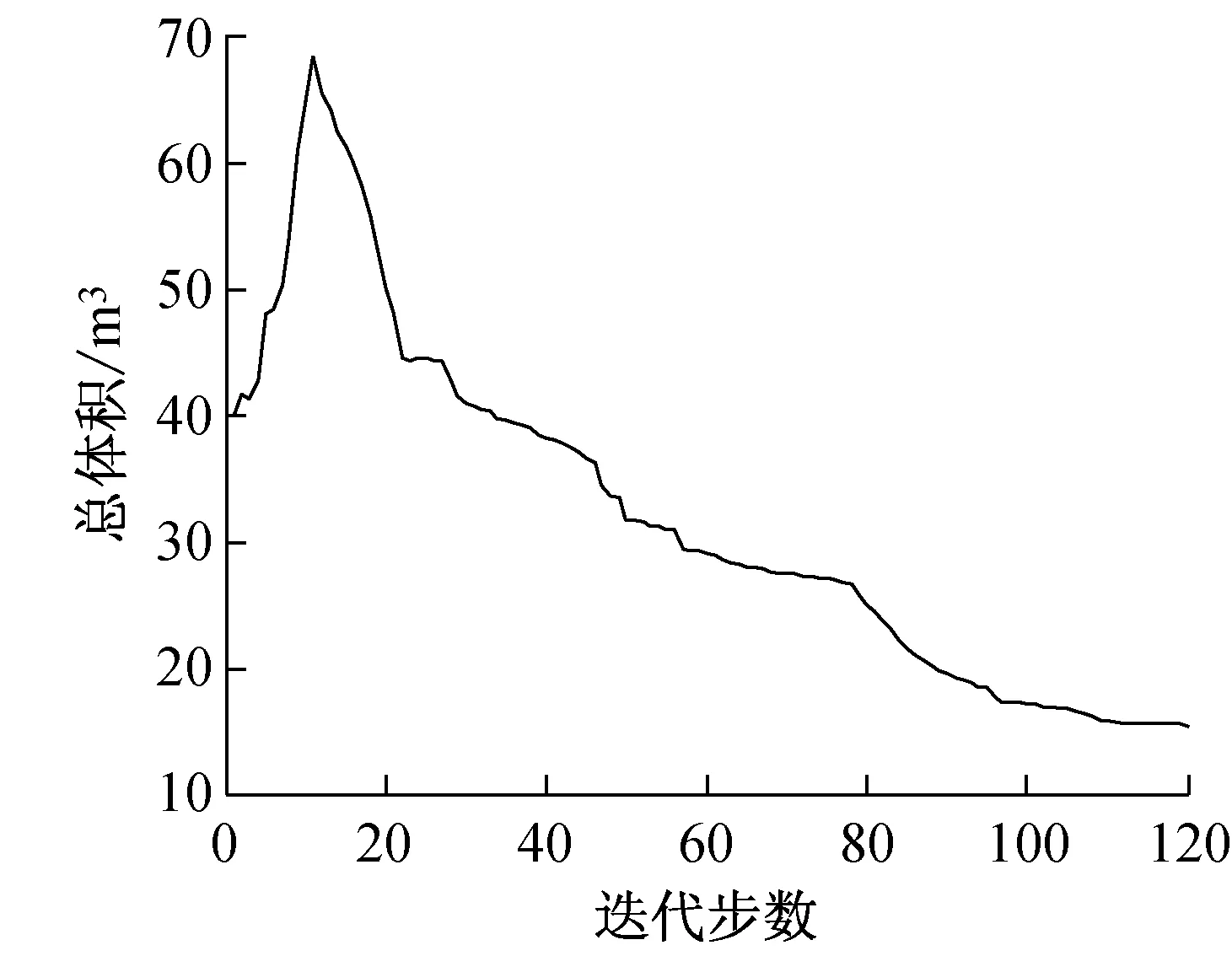
(a) 总体积收敛曲线

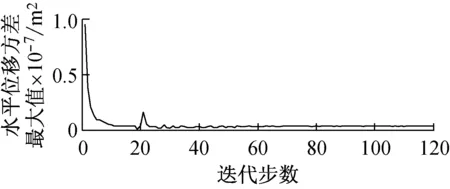
(b) 水平位移方差最大值收敛曲线

(c) 竖向位移方差最大值收敛曲线

Fig.6 Convergence curve of structure’s total volume and the maximum horizontal and vertical displacement variance of pointAin the process of optimization

表2 优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积

Fig.2 Maximum horizontal and vertical displacement variance at constraint point before and after optimization and structure’s total volume

σ2AVmaxσ2AHmax总体积优化前9.5×10-84.6×10-1040优化后3.8×10-97.0×10-1115.44

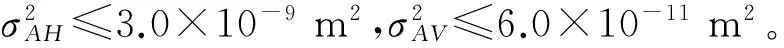
优化后的结构如图7所示,优化目标和约束条件的迭代曲线如图8所示,优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积见表3。

图7 桁架结构截面与节点坐标优化结果

算例2 平面输电塔优化

优化后的结构如图10所示，优化目标和约束条件的收敛曲线，如图11所示，优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积见表4。

以上优化过程中对杆件截面积小于某一阀值时进行杆件删除，同时对节点优化中出现重叠的杆件和节点进行合并处理。

(a) 总体积收敛曲线

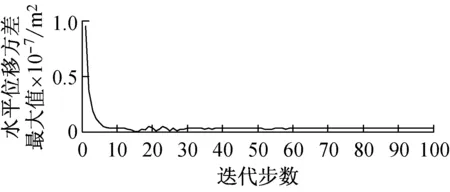
(b) 水平位移方差最大值收敛曲线

(c) 竖向位移方差最大值收敛曲线

Fig.8 Convergence curve of structure’s total volume and the maximum displacement variance at pointAin the process of optimization

表3 优化前后约束点处水平位移方差最大值、竖向位移方差最大值及结构总体积

Fig.3 Maximum horizontal and vertical displacement variance at constraint point before and after optimization and structure’s total volume

σ2AVmaxσ2AHmax总体积优化前9.5×10-84.6×10-1040优化后3.0×10-95.9×10-1112.37

表4 化前后A、C点处水平位移方差最大值、竖向位移方差最大值及结构总体积

Fig.4 Maximum horizontal and vertical displacement variance at pointAand pointCbefore and after optimization and structure’s total volume

从整个优化过程来看，优化初期为了满足位移约束条件，结构总体积增加，节点坐标变化较缓慢，当约束条件满足后结构总体积快速下降，节点坐标变化较大。从设计变量来看，同时考虑杆件截面积及节点坐标的优化结果最为合理。而优化效率及精度与所选取的积分步长有一定关系，这些需要在优化过程中进行权衡处理。

图9 优化前结构Fig.9 Initialdesign图10 优化后结构Fig.10 Theoptimizedstructure

(a)

(b)

(c)

(d)

(e)

4 结 论

本文首先应用基于Newmark-β积分格式的时域显式法求解随机响应对设计参数灵敏度，再利用GCMMA算法求解非平稳地震荷载作用下桁架结构的形状与拓扑优化问题。考虑桁架结构同时受水平和竖向地震作用，建立以体积为目标，节点的水平和竖向位移方差的最大值为约束，优化桁架结构的截面积及节点坐标。优化结果表明使用该方法既减小了结构的位移响应又降低了结构用料的目的。总体来看，基于Newmark-β积分格式的时域显式法求解随机响应对设计参数灵敏度方面高效精确，从而可以有效结合GCMMA算法对桁架结构进行合理的形状和拓扑优化。最后，通过36杆平面桁架结构和平面输电塔的优化算例验证该方法切实可行。

[1] RONG Jianhua, TANG Zhili. Topological optimization design of structures under random ex-citations using SQP method[J]. Engineering Structures, 2013(56): 2098-2106.

[2] 张桥,张卫红,朱继宏.动力响应约束下的结构拓扑优化设计[J]. 机械工程学报,2010, 46(15): 45-51.

ZHANG Qiao, ZHANG Weihong, ZHU Jihong. Topology optimization of structures under dynamic response constraints[J]. Journal of Mechanical Engineering, 2010, 46(15): 45-51.

[3] ZHANG Qiao, ZHANG Weihong, ZHU Jihong, et al. Layout optimization of multi-component structures under static loads and random excitations[J]. Engineering Structures, 2012(43): 120-128.

[4] LI Ming, TANG Wencheng, YUAN Man. Structural dynamic topology optimization based on dynamic reliability using equivalent static loads[J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 121-129.

[5] 潘晋,王德禹.动力响应约束下的桁架结构拓扑优化[J]. 振动与冲击,2006, 25(4):8-12.

PAN Jin, WANG Deyu. Topology optimization of truss structure under dynamic response constraints[J]. Journal of Vibration and Shock, 2006, 25(4): 8-12.

[6] JOG C S. Topology design of structures subjected to periodic loading[J]. Journal of Sound and Vibration, 2002, 253(3): 687-709.

[7] HAJIRASOULIHA I, PILAKOUTAS K, MOGHADDAM H. Topology optimization for the seismic design of truss-like structures[J]. Computers & Structures, 2011, 89(7/8): 702-711.

[8] RONG J H. Topology optimization of structures under dynamic response constraints[J]. Journal of Sound and Vibration, 2000, 234(2): 177-189.

[9] GOMES H M. Truss optimization with dynamic constraints using a particle swarm algorithm[J]. Expert Systems with Applications, 2011, 38(1): 957-968.

[10] MA Juan, GAO Wei, WRIGGERS P, et al. Structural dynamic optimal design based on dynamic reliability[J]. Engineering Structures, 2011, 33(2): 468-476.

[11] MIGUEL L F F, FADEL MIGUEL L F. Shape and size optimization of truss structures considering dynamic constraints through modern metaheuristic algorithms[J]. Expert Systems with Applications, 2012, 39(10): 9458-9467.

[12] 房占鹏,郑玲,唐重才,等.指定频带简谐激励下约束阻尼结构拓扑优化[J]. 振动与冲击,2015,34(14):135-141.

FANG Zhanpeng, ZHENG Ling, TANG Zhongcai, et al. Topology optimization for constrained layer damping structures under specified band harmonic excitations[J]. Journal of Vibration and Shock, 2015, 34(14): 135-141.

[13] 苏成,徐瑞.非平稳随机激励下结构随机振动时域分析法[J].工程力学,2010,27(12):77-83.

SU Cheng, XU Rui. Random vibration analysis of structures subjected to non-stationary excitations by time domain method[J]. Engineering Mechanics, 2010,27(12):77-83.

[14] 苏成,徐瑞.非平稳随机激励下结构体系动力可靠度时域解法[J]. 力学学报,2010,42(3):512-520.

SU Cheng, XU Rui. Time-domain method for dynamic reliability of structural systems subjected to non-stationary random excitations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 512-520.

[15] 陈太聪,苏成,胡志强,等.非平稳随机响应灵敏度分析的时域显式法[J]. 振动工程学报,2015,28(4):43-49.

CHEN Taicong, SU Cheng, HU Zhiqiang, et al. An explicit time-domain method in sensitivity analysis of non-stationary stochastic responses[J]. Journal of Vibration Engineering, 2015, 28(4): 43-49.

[16] SVANBERG K. A class of globally convergent optimization methods based on conservative convex separable approximations[J]. SIAM Journal on Optimization, 2002，12(2): 555-573.

[17] 余超.基于时域显式法的结构瞬时最优控制[D].广州：华南理工大学, 2015.

[18] SU Cheng, HUANG Huan, MA Haitao, et al. Random vibration analysis of hysteretic systems by explicit iteration Monte-Carlo simulation method[J]. Earthquakes and Structures, 2014, 7(2): 119-139.

[19] CACCIOLA P, COLAJANNI P, MUSCOLINO G. A modal approach for the evaluation of the response sensitivity of structural systems subjected to non-stationary random Processes[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(42/43/44): 4344-4361.

Shape and topology optimization of truss structures under non-stationary stochastic seismic excitations

LI Xueping, LI Donghong, WEI Peng, SU Cheng

(State Key Laboratory of Subtropical Building Science, School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China)

Aiming at the dynamic optimization problems of truss structures under non stationary random seismic actions, the sensitivities of non stationary random responses of a truss structure to design parameters were derived based on the time-domain explicit method. The cross-section areas and nodal coordinates of the truss structure were optimized combined with the method of moving asymptotes. The volume of the truss was taken as the objective function and the displacement variances under actions of horizontal and vertical earthquakes were taken as the constraints to establish an optimization model. Two numerical examples illustrated the feasibility and effectiveness of the proposed method for dynamic shape and topology optimization of truss structures under non-stationary stochastic seismic excitations.

truss; non-stationary; topology optimization; time-domain explicit method

国家自然科学基金项目(11002056；11372004)；中央高校基本科研业务费项目(2014ZZ0071)

2015-10-22 修改稿收到日期：2016-03-02

李雪平 男，博士,副研究员，1978年生

苏成 男，博士，教授，1968年生 E-mail: cvchsu@scut.edu.cn

TU311；O324

A

10.13465/j.cnki.jvs.2017.09.021