基于多元Copula函数的桥梁体系地震易损性分析方法研究

宋 帅， 钱永久， 吴 刚

(1.西南交通大学 土木工程学院, 成都 610031；2. 东南大学 交通学院， 南京 210096)

基于多元Copula函数的桥梁体系地震易损性分析方法研究

宋 帅1， 钱永久1， 吴 刚2

(1.西南交通大学 土木工程学院, 成都 610031；2. 东南大学 交通学院， 南京 210096)

为了考虑桥墩、支座等构件地震需求之间相关性，引入多元Copula函数对构件地震需求之间的相关结构进行描述，提出了桥梁体系易损性分析的新方法。基于增量动力分析结果建立了单个构件的易损性，采用核光滑方法对各构件的边缘分布函数进行估计；基于离差平方和最小准则和最小距离法对多元Copula函数进行了参数估计及优选；结合单个构件的易损性及多元Copula函数，建立了桥梁体系的易损性曲线，分析了构件地震需求之间相关性对桥梁体系易损性的影响。结果表明：桥墩、支座等构件地震需求之间的相关性对桥梁体系易损性影响显著；基于离差平方和最小准则构造的多元Copula函数，能够准确描述构件地震需求之间的相关结构，有效降低桥梁体系易损性分析的难度。

桥梁体系；地震易损性；多元Copula函数；地震需求相关性；离差平方和最小；核光滑方法

在地震作用下，桥墩、支座及桥台等桥梁构件地震需求之间相互影响，不可避免地存在一定的相关性[1]。当地震动强度不同时，构件需求之间的相关性也不同，特别是当结构响应进入塑性阶段以后，构件地震需求之间的相关性变得更加复杂[2]。然而，由于建立构件地震需求的联合分布函数较为困难，准确模拟构件地震需求之间相关性的易损性研究较少[3-4]。Yang等[5-7]在对桥梁体系易损性进行分析时，假定桥墩、支座等构件地震需求之间完全相关或者完全不相关，进而得到桥梁体系易损性的上、下边界。但是，随着构件数量及失效模式的增加，假定构件需求之间完全相关或完全不相关，得到的桥梁体系易损性误差较大[8]。Ramanathan等[9-10]基于构件地震需求之间的相关系数矩阵，采用Monte Carlo抽样方法模拟构件地震需求之间的相关性，建立了桥梁体系的易损性曲线。但该方法通常假设构件地震需求服从对数正态分布，且计算量较大[11]。因此，如何准确、高效地模拟构件地震需求之间的相关性，是桥梁体系易损性分析的关键问题。

Copula函数作为处理变量之间相关性的重要手段，已经在机械、水利工程领域得到广泛的应用[12-13]。作为联合分布函数与边缘分布函数的连接函数，Copula函数不仅能够描述变量之间的复杂的非线性相关关系，其边缘分布函数的形式亦不受限制[14]。

本文通过对地震动-桥梁样本的增量动力分析(Incremental Dynamic Analysis，IDA)结果进行统计分析，建立了桥墩、支座等单个构件的易损性曲线，并采用核光滑方法对各构件的边缘分布函数进行估计；基于离差平方和最小准则及最小距离法对多元Copula函数的参数进行估计及优选；选择合适的多元Copula函数，描述了桥墩、支座等多个构件地震需求之间的相关性，提出了桥梁体系易损性分析的新方法，分析了桥墩、支座等构件地震需求之间的相关性对桥梁体系易损性的影响。

1 基于多元Copula函数桥梁体系易损性分析

1.1 体系易损性分析

桥梁体系通常是由桥墩、桥台及支座等主要构件组成，其中任一构件的破坏均会影响桥梁的使用功能，因此将桥梁体系定义为串联体系，进而得到桥梁体系的易损性Pfs

(1)

式中：Pi(·)为构件i的易损性；m为体系中的构件数量。

由式(1)可知，桥梁体系的易损性是构件易损性的并集，但是由于构件地震需求之间相关性的影响，构件易损性之间并非相互独立，桥梁体系易损性不是单个构件易损性的简单相加。在这种情况下，由可靠性理论可知，式(1)可进一步表示为

(-1)m-1P(X1X2…Xm,IM)

(2)

式中：P(Xi,IM)为在某一地震动强度IM下单个构件的易损性；P(XiXj,IM)为两个构件同时破坏的易损性，以此类推；P(X1，X2，…，Xm,IM)为m个构件同时破坏的易损性。其中：单个构件的易损性P(Xi,IM)可以定义为构件Xi的地震需求Sdi超过构件Xi性能指标Sci的概率[15]

(3)

为克服构件地震需求及构件性能指标服从对数正态分布假设的限制，可以对地震动-桥梁样本进行增量动力分析(IDA)，基于概率的方法对每级增量水平下分析结果进行统计，得到单个构件Xi的易损性

(4)

式中：nXi,IM为在地震动强度IM下构件Xi失效的样本数；NXi,IM为地震动强度IM下构件Xi的样本总数。

由于构件易损性并非相互独立，直接求解两个或多个构件同时破坏的易损性较为困难。为此，本文引入多元Copula函数方法来对式(2)进行求解。

1.2 多元Copula函数的定义

N元Copula函数是指具有以下性质的函数C(·,…,·)[14]：

(1) 定义域为IN，即[0,1]N；

(2)C(·,…,·)有零基面且是N维递增的；

(3)C(·,…,·)的边缘分布函数为C(·)，n=1,2,…,N，且

Cn(un)=C(1,…,1,un,1,…,1)=un

(5)

式中，un∈[0,1]，n=1,2,…,N。

若F(·,…,·)为联合分布函数，其边缘分布函数为F1(·),F2(·),…,FN(·)，那么存在一个Copula函数C(·,…,·)，满足

F(x1,x2…,xN)=C(F1(x1),F2(x2),…,FN(xN))

(6)

反之，若F1(·),F2(·),…,FN(·)为一元分布函数，C(·,…,·)为相应的Copula函数，则F(·,…,·)为具有边缘分布函数F1(·),F2(·),…,FN(·)的联合分布函数。

由以上性质可知，基于Copula函数，可以用边缘分布函数对联合分布函数进行显式表达，并将变量之间的相关结构和边缘分布函数进行分离，进而简化联合概率分布函数的求解。由于Copula函数的边缘分布形式灵活，同一个Copula函数，其边缘分布可以为不同类型的分布；作为各边缘分布的连接函数，Copula函数的形式也不受边缘分布的限制。

当变量单调变换时，即若

(7)

则有

C(x1,x2,…,xN)=C(h1(x1),h2(x2),…,hN(xN))

(8)

式中，hn(xn)为随机变量xn的函数。

由式(8)可知，Copula函数在变量单调增变换下，形式不会发生变化。此外，Copula函数的形式多样：从结构上说，既可以是对称的，也可以是非对称的；从相依性上讲，可以是上尾相依，也可以是下尾相依。和线性相关系数相比，Copula函数能够描述构件之间的非线性、非对称、上尾相依、下尾相依等各种类型的复杂相关结构，具有普遍的适用性。

由多元Copula函数的性质可知，系统中任意k个构件同时破坏的易损性可由单个构件的易损性进行定义

P[X1,X2,…,Xk,IM]=C(u1,u2,…,uk,IM)

(9)

式中：ui为单个构件Xi的易损性；C(·)为多元Copula函数。通过式(9)可将构件地震需求之间的相关结构和构件的易损性进行分离，进而简化多个构件同时破坏易损性的求解。将式(9)代入式(2)，即可得到桥梁体系的易损性Pfs

(-1)m-1C(P1,P2,…,Pm,IM)

(10)

1.3 多元Copula函数的选择

由式(9)可知，采用多元Copula函数求解多个构件同时破坏易损性的关键是选择合适的Copula函数类型，以准确描述构件地震需求之间的相关结构，进而建立桥梁体系的易损性曲线。

实际中常用的Copula函数主要包括Elliptic Copula类和Archimedean Copula类。由于Archimedean Copula函数具有对称性和可结合性，在多元情况下计算较为简便。本文选取三种常见的Archimedean Copula函数作为备选函数，三种Copula函数的表达式为

(1)N元Clayton Copula函数

C(u1,u2,…,un;θ1)=

(11)

(2)N元Gumbel Copula函数

C(u1,u2,…,un;θ2)=

(12)

(3)N元Frank Copula函数

C(u1,u2,…,un;θ3)=

θ3≠0;N≥3,θ3∈(0,∞)

(13)

式中：θi为相关参数；ui为边缘分布函数。基于地震动-桥梁样本的增量动力分析数据，可以通过离差平方和最小准则对多元Copula函数进行参数估计；在此基础上，可以采用最小距离法，从以上三种备选Copula函数中，选择合适的Copula函数，来准确描述桥墩、支座等构件地震需求之间的相关结构。主要步骤如下：

步骤1 确定构件的边缘分布函数

根据统计分析的基本要求，建立一定数量的地震动-桥梁样本，进行增量动力分析(IDA)。根据构件地震需求的样本值及性能指标，对各构件的边缘分布函数进行估计，得到各构件的边缘分布函数。

步骤2 Copula函数参数估计

基于构件地震需求样本点处的边缘分布函数值，采用离差平方和最小准则，对多元Copula函数进行参数估计，得到多元Copula函数相关参数的估计值。

步骤3 Copula函数的优选

基于Copula函数相关参数的估计值，采用最小距离法对三种备选Copula函数的拟合度进行检验，选择合适的多元Copula函数，描述构件地震需求之间的相关结构。

2 计算实例

2.1 结构模型

以某高铁线路上一跨径为(36 m+64 m+36 m)连续梁桥为例，阐述基于多元Copula函数的桥梁体系易损性分析新方法。主梁为变截面箱梁，顶板宽12.2 m，底板宽6.7 m，中墩处梁高6.0 m，跨中部位梁高3.2 m，采用C55混凝土。桥墩采用圆端形实体截面，墩高18 m，混凝土材料为C40，保护层厚度为50 mm，纵向钢筋和箍筋都采用HRB335级钢筋，纵筋直径25 mm，配筋率为0.4%，箍筋直径12 mm，配箍率为0.3%；中墩截面尺寸为3.7 m×8.5 m，边墩截面尺寸为3.6 m×7.0 m。桥梁支座采用固定型和纵向滑动型球形支座。基础采用直径1.5 m灌注桩，桩长30 m，梅花型布置，间距为4 m。场地类型为Ⅱ类。

采用OpenSees程序建立桥梁的有限元模型。主梁在地震下基本处于弹性状态，采用弹性梁柱单元模拟；桥墩可能发生塑性破坏，采用非线性纤维梁柱单元模拟，保护层混凝土和核心区混凝土采用基于Kent-Scott-Park本构模型的Concrete01材料分别进行定义，以考虑核心区混凝土的约束效应；钢筋采用基于Giuffré-Menegotto-Pinto本构模型的Steel02材料模拟；支座采用零长度单元进行模拟，其本构关系采用理想弹塑性模型，模型参数根据支座的型号及尺寸，参考文献[16]进行计算；桥墩基础采用零长度单元进行模拟，单元的平动及转动刚度，根据桩周土层条件，采用m法计算得到。桥梁结构的有限元模型，如图1所示。

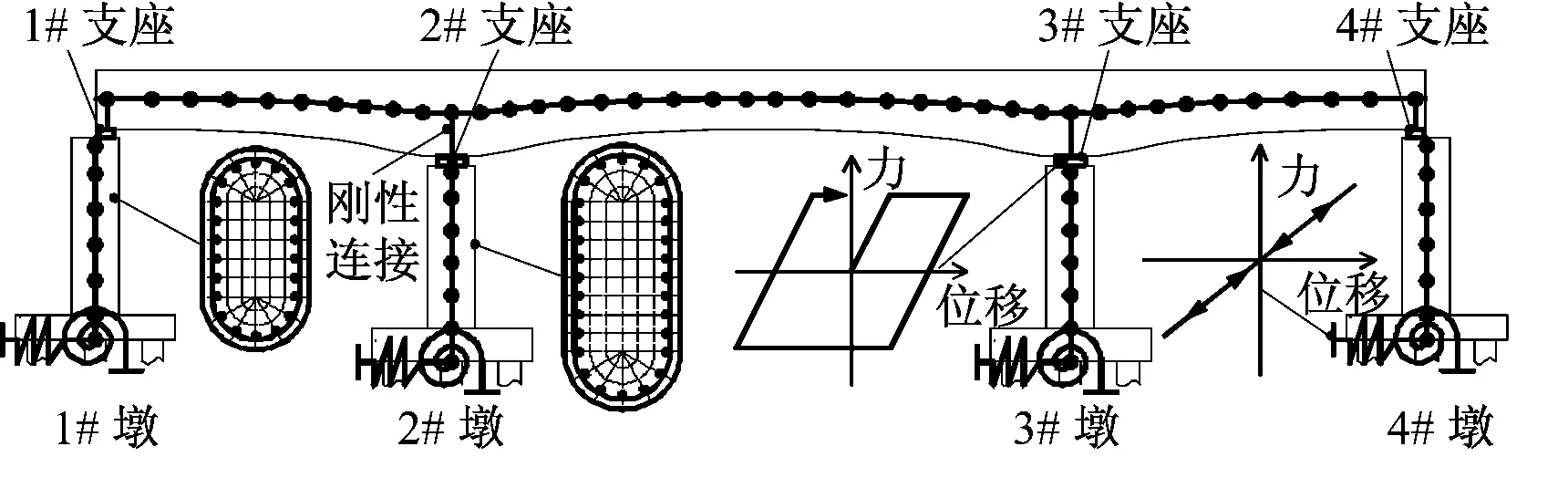
图1 桥梁结构的分析模型

2.2 增量动力分析

2.2.1 地震动-桥梁样本

地震动-桥梁样本是增量动力分析的基础，而在样本抽样的过程中需要考虑地震动不确定性及结构参数不确定性。地震动不确定性包括地震动本身的随机性以及方向效应、入射角及空间变异性[17]，属于偶然不确定性范畴。为综合考虑地震动的不确定性，从太平洋地震工程中心强震数据库中选取符合Ⅱ类场地的地震动，所选地震动满足以下原则：

(1) 震级≥5.5级；

(2) 震中距<100 km；

(3) 地震动两个水平方向分量高通滤波角频率<0.2 Hz，低通滤波角频率>18 Hz；

(4) 选取地震动的剪切波速范围为260 m/s≤VS30≤500 m/s。

所选地震动的峰值加速度分布，如图2所示。在此基础上，采用区间法[18]以震级(6.5)和震中距(30 km)将所选的地震动分为4组，每组包含25条不同震级-震中距组合的地震动，进而将地震动在不同的震级及震中距范围内进行离散，结合地震动选取过程中其幅值、频谱、持时特性的离散性，即可在增量动力分析中考虑地震动幅值、频谱、持时特性以及震级、震中距的不确定性。

图2 地震动的PGA分布

结构参数的不确定性主要包括材料强度、几何尺寸、质量、阻尼以及边界条件等，属于认知不确定性范畴。研究表明：桥梁地震需求主要受混凝土强度、钢筋强度、滑动支座摩擦因数、结构阻尼、上部结构质量以及边界条件等因素的影响[19]。对主要的结构参数不确定性及其概率分布进行总结，如表1所示。

根据以上结构参数不确定性的概率分布特征，将各个参数的5%～95%概率区间等概率地分成100组，采用拉丁超立方抽样方法[20]对以上分组进行分层抽样，即可建立100组桥梁样本。和区间法得到的100条地震动记录进行随机配对，组成100组地震动-桥梁样本，即可以在结构的概率地震需求分析中，综合考虑地震动及结构参数的不确定性。

表1 结构参数不确定性及其分布

2.2.2 构件地震需求

以往的震害表明，对于中小跨径桥梁，支座及桥墩是最薄弱的环节[21]。以桥墩纵、横桥向位移延性比(μL、μT)以及支座纵、横桥向位移(bL、bT)作为结构的地震需求参数，可有效地描述桥梁的破坏状态及损伤程度。为了得到桥梁在地震作用下的整个破坏状态，采用增量动力分析方法(IDA)，将每条地震动记录的峰值加速度调整为0.1～1.5g，增量水平为0.1g，通过对每组地震动-桥梁样本进行IDA分析，得到构件的地震需求样本值，对其进行统计分析得到构件地震需求的中位值，如图3所示。

(a) 桥墩

(b) 支座

2.3 构件易损性曲线

2.3.1 极限状态性能指标

桥梁在地震作用下的破坏一般可分为轻微、中等、严重和完全四种状态。为了对各破坏状态下的易损性进行评估，需要定义构件在各破坏状态下的性能指标。对于桥墩，四种破坏状态分别对应于纵向钢筋首次屈服、保护层混凝土压碎、核心区混凝土开裂破坏及纵向钢筋屈曲。各破坏状态下桥墩的位移延性比μi定义为

(14)

式中：Δi为各破坏状态下墩顶极限位移；Δy为纵向钢筋首次屈服时的墩顶位移。对截面进行弯矩-曲率分析，即可得到各破坏状态下桥墩的位移延性指标，如表2所示。

支座的四种破坏状态可以采用位移进行定义，对于活动支座，根据支座的几何尺寸及物理参数，分别取设计位移、1.5倍的设计位移、2.0倍的设计位移及1/2球面滑板直径作为轻微破坏、中等破坏、严重破坏及完全破坏的性能指标；固定支座的容许位移较小，分别取10 mm、15 mm、20 mm及50 mm作为四种破坏状态的性能指标，如表2所示。

由于结构参数不确定性的影响，构件的性能指标存在一定的变异性，可采用Nielson[22]提出的变异系数(Coefficient of Variation，COV)进行描述。轻微和中等破坏下，变异性较小，变异系数取0.25；严重和完全破坏下，变异性较大，变异系数取0.5，如表2所示。

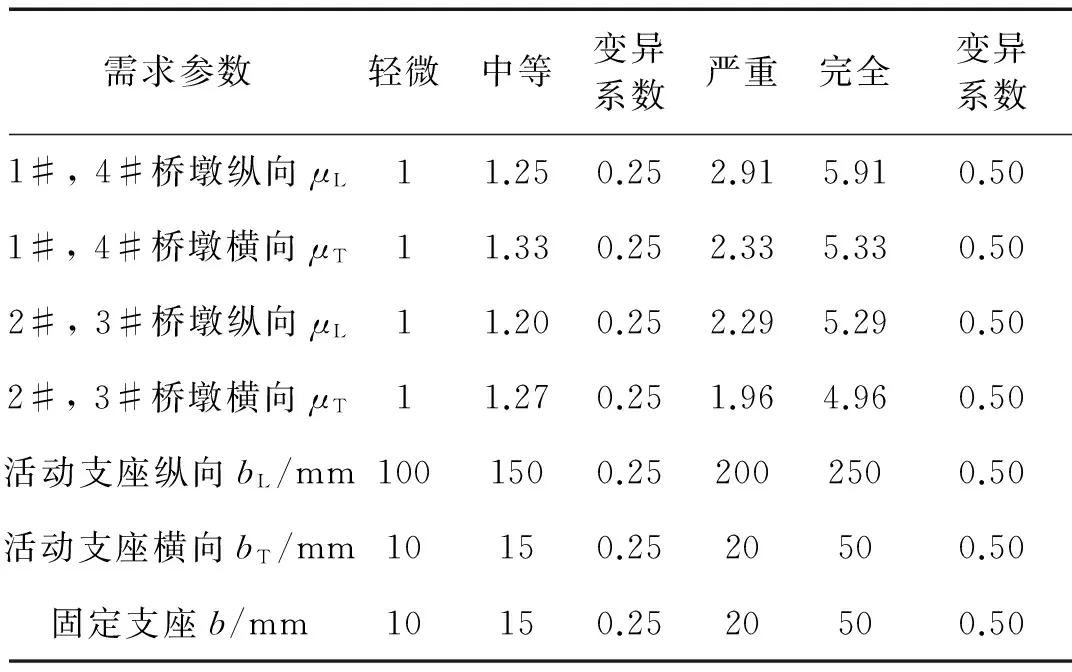
表2 构件性能指标

2.3.2 构件易损性

为了避免构件地震需求概率分布形式假定引起的误差，本文基于式(4)，直接对构件的功能函数进行概率统计，计算构件的易损性。

构件的功能函数是指构件的地震需求与和构件的性能指标之差，主要用来判断构件是否失效。当构件的功能函数值>0，表示构件地震需求超过某一破坏状态下的性能指标，构件失效。基于IDA分析结果和构件的性能指标，对每级增量水平下构件的功能函数进行统计分析，即可得到各破坏状态下构件的易损性。限于篇幅，仅给出桥墩、支座在轻微破坏状态下的易损性曲线，如图4所示。

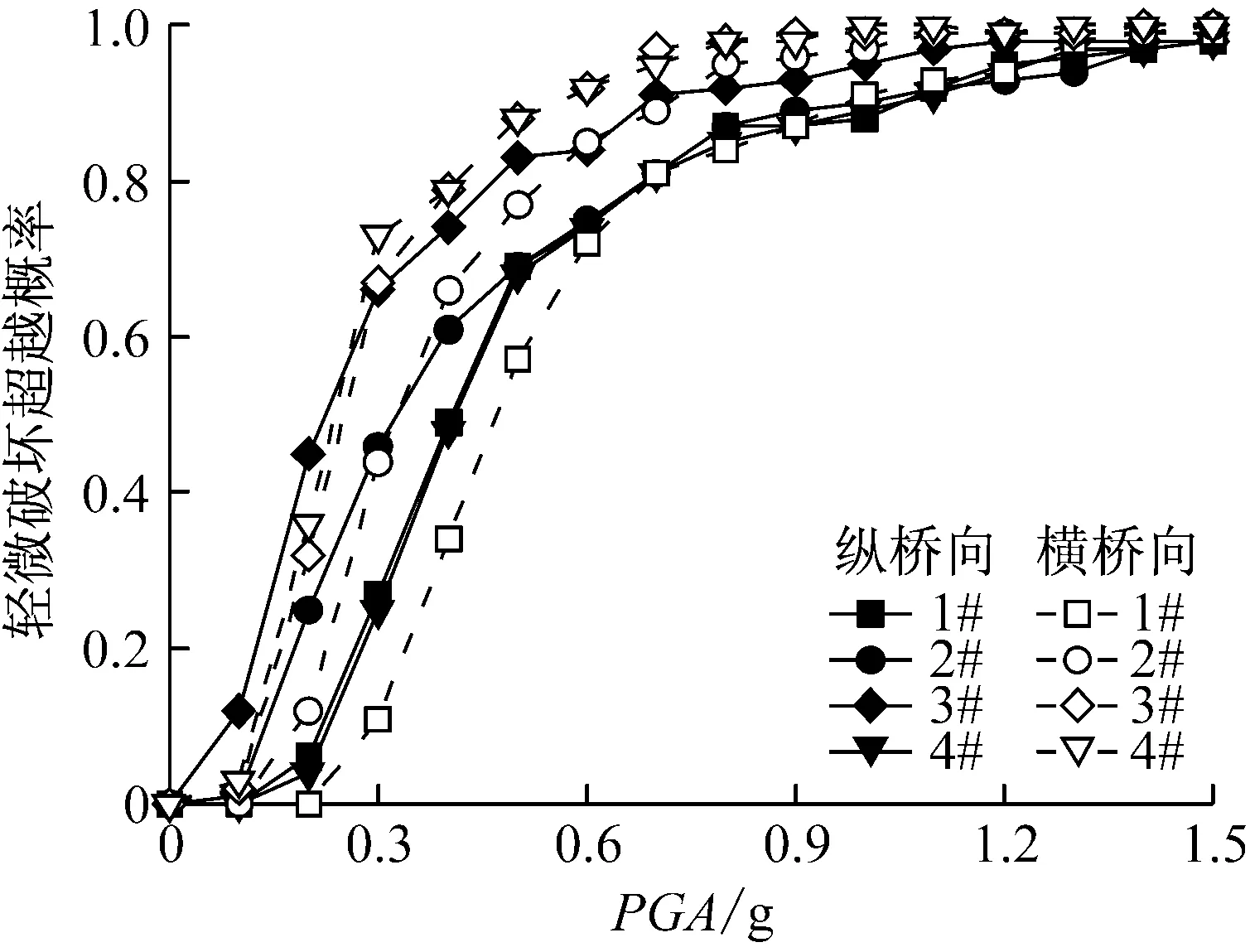
(a) 桥墩

(b) 支座

2.4 多元Copula函数的参数估计及模型选择

2.4.1 构件边缘分布函数估计

基于IDA分析结果，采用核光滑方法[23]对构件的边缘分布函数进行估计，核光滑法是用来估计分布函数或密度函数一种非参数估计方法。即基于样本观测数据本身来确定总体的概率分布，而不需要事先对构件边缘分布的形式进行假定。通过选择合适的核函数及窗宽，即可得到构件的边缘分布函数。由于不需要事先对构件的边缘分布函数形式进行假定，得到的边缘分布函数更加符合实际。限于篇幅，仅给出桥墩、支座在轻微破坏状态下的边缘分布函数，如图5所示。

2.4.2 多元Copula函数参数估计

极大似然估计是最为常用的参数估计方法，然而由于多元Copula函数的概率密度函数求解涉及到多元函数微分，采用极大似然估计方法进行参数估计存在一定的困难。因此，本文提出基于离差平方和最小准则，对多元Copula函数进行参数估计，避免了对多元Copula函数进行微分运算。

(a) 桥墩

(b) 支座

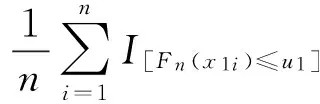
(15)

式中：u1,u2,…,um∈[0,1]；I[·]为示性函数，当Fn(xmi)≤um时，I[Fn(xmi)≤um]=1，否则I[Fn(xmi)≤um]=0。基于离差平方和最小准则，得到多元Copula函数的参数估计式为

OLS=

(16)

将各构件的边缘分布函数及多元经验Copula函数代入式(16)，采用非线性优化技术进行求解，得到多元Copula函数相关参数的估计值，如表3所示。

2.4.3 多元Copula函数的模型选择

采用基于平方欧式距离的最小距离法对多元Copula函数的拟合度进行检验，选择最优Copula函数，描述构件地震需求之间相关结构。平方欧式距离d2定义为

(17)

基于式(17)计算各备选Copula函数与经验Copula函数的平方欧式距离，如表3所示。对比可知，在各破坏状态下，多元Frank Copula函数的平方欧式距离均最小。因此，多元Frank Copula函数是描述桥墩、支座等构件地震需求之间相关结构的最优Copula函数。

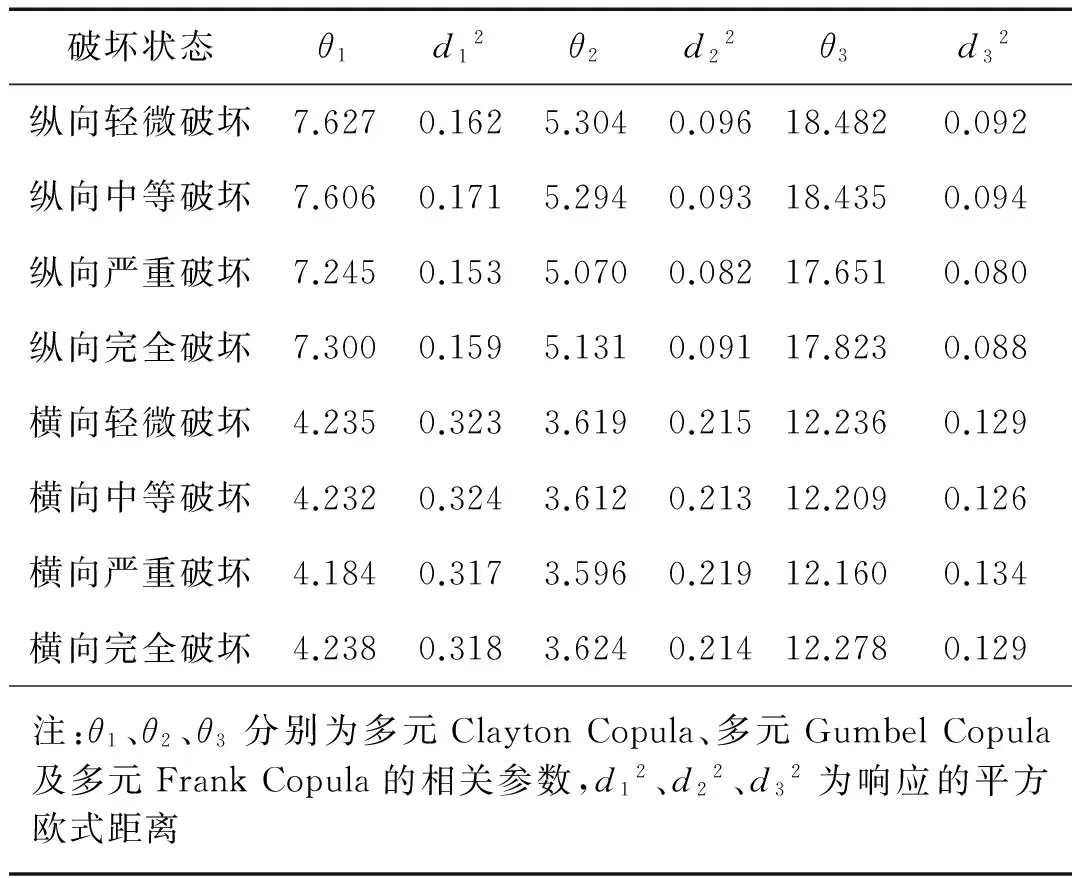
表3 多元Copula函数的参数

2.5 体系易损性曲线

2.5.1 基于多元Copula函数的体系易损性

将表3中多元Frank Copula函数的参数估计值代入式(13)，即可得到构件地震需求之间的相关结构；结合“2.3.2”节得到的单个构件易损性和构件之间的相关结构，由式(9)得到多个构件同时失效的易损性；在此基础上，将单个构件的易损性及多个构件同时失效的易损性代入式(10)，即可得到考虑构件地震需求之间相关性影响的桥梁体系易损性曲线，如图6所示。

2.5.2 基于Monte Carlo方法的体系易损性

为了对多元Copula函数方法进行验证，采用Monte Carlo方法对桥梁体系的易损性进行分析。Monte Carlo方法是目前学者分析结构体系易损性主要采用的一种数值抽样方法，其结果位于一阶界限法的上、下界之间，当抽样数量较大时，可将其作为近似精确值。在每级增量水平下，基于桥墩、支座等构件地震需求样本值，计算构件地震需求之间的相关系数并拟合各构件地震需求的概率分布函数；在此基础上，对多个构件地震需求同时进行随机抽样以考虑构件地震需求之间相关性的影响，抽样次数取N=105次；将构件地震需求的抽样值和构件的性能指标相减，得到构件的功能函数；对构件功能函数的样本值进行统计分析，得到桥梁体系的失效样本数，将其除以桥梁体系的样本总数，即可得到桥梁体系的失效概率。对不同破坏状态各增量水平下的失效概率依次进行分析，即可得到桥梁体系的易损性曲线，为便于对比，将其列于图6。

2.5.3 结果验证

对比多元Copula函数方法和Monte Carlo方法得到的桥梁体系易损性，由图6可知：纵桥向，四种破坏状态下二者的偏差最大分别为5.02%、7.83%、6.25%及6.90%；横桥向，四种破坏状态下二者的偏差最大分别为7.43%、6.82%、7.62%及5.29%。由此可见，两种方法得到的桥梁体系易损性吻合良好，表明多元Copula函数方法的精度较高，结果稳定可靠。此外，多元Copula函数能够避免大量的数值抽样，使桥梁体系易损性计算的效率显著提高。

(a) 纵桥向

(b) 横桥向

3 构件需求相关性对桥梁体系易损性的影响

为分析桥墩、支座等构件地震需求之间的相关性对桥梁体系易损性的影响，计算构件完全相关和完全不相关情况下的桥梁体系易损性。由可靠性理论可知，当构件地震需求完全相关时，桥梁体系易损性等于单个构件易损性的最大值，即

(18)

当构件地震需求完全不相关时，各构件地震需求为相互独立的变量，桥梁体系易损性为

(19)

式中：Pfs为桥梁体系的易损性；Pi为构件i的易损性；m为构件数量。将桥墩、支座等单个构件的易损性代入式(18)、式(19)，即可得到构件完全相关和完全不相关情况下桥梁体系的易损性，并与Frank Copula函数对比，如图7所示。

由图7可知，假设桥墩、支座等构件地震需求之间完全相关，得到的体系易损性偏小。在纵桥向，四种破坏状态下最大偏差分别为-6.5%、-9.9%、-14.7%、-2.7%；在横桥向，四种破坏状态下最大偏差分别为-3.2%、-6.1%、-8.0%、-12.0%。假设桥墩、支座等构件地震需求之间完全不相关，得到的体系易损性明显偏大。在纵桥向，四种破坏状态下最大偏差分别为33.9%、34.1%、38.1%、34.8%；在横桥向，四种破坏状态下最大偏差分别为20.6%、15.2%、23.0%、35.0%。由此可见，桥墩、支座等构件地震需求之间的相关性对桥梁体系易损性影响显著；准确描述桥墩、支座等构件地震需求之间的相关性十分必要。

4 结 论

基于离差平方和最小准则和最小距离法，构造了描述桥墩、支座等构件地震需求相关性的多元Copula函数，提出了桥梁体系易损性分析的新方法，研究了构件地震需相关性对桥梁体系易损性的影响，结果表明：

(1) 对于连续梁桥，多元Frank Copula函数能够准确地描述桥墩、支座等构件地震需求之间的相关结构，简化了多个构件同时破坏易损性的求解，从而保证在桥梁体系易损性分析中准确考虑构件地震需求之间相关性的影响。

(2) 采用离差平方和最小准则对多元Copula函数进行参数估计，避免了极大似然估计中多元函数微分运算，有效降低了多元Copula函数的构造难度。

(3) 桥墩、支座等构件地震需求之间的相关性对桥梁体系易损性影响显著；准确描述桥墩、支座等构件地震需求之间的相关性十分必要。

(4) 作为处理构件地震需求之间相关性的一种重要手段，多元Copula函数应用范围并不局限于连续梁桥，对于其他的工程结构同样适用，在实际应用中，应针对具体的结构形式，选择合适的Copula函数模型对构件之间的相关结构进行准确描述。

本文采用多元Copula函数描述了桥墩、支座等多个构件地震需求之间的相关性。然而，随着龄期的增长，桥梁性能的不断退化，桥墩、支座等构件之间的相关性也随之发生变化，如何考虑构件之间相关性的时变特性，进而建立更为精确的桥梁体系时变易损性曲线还需深入研究。

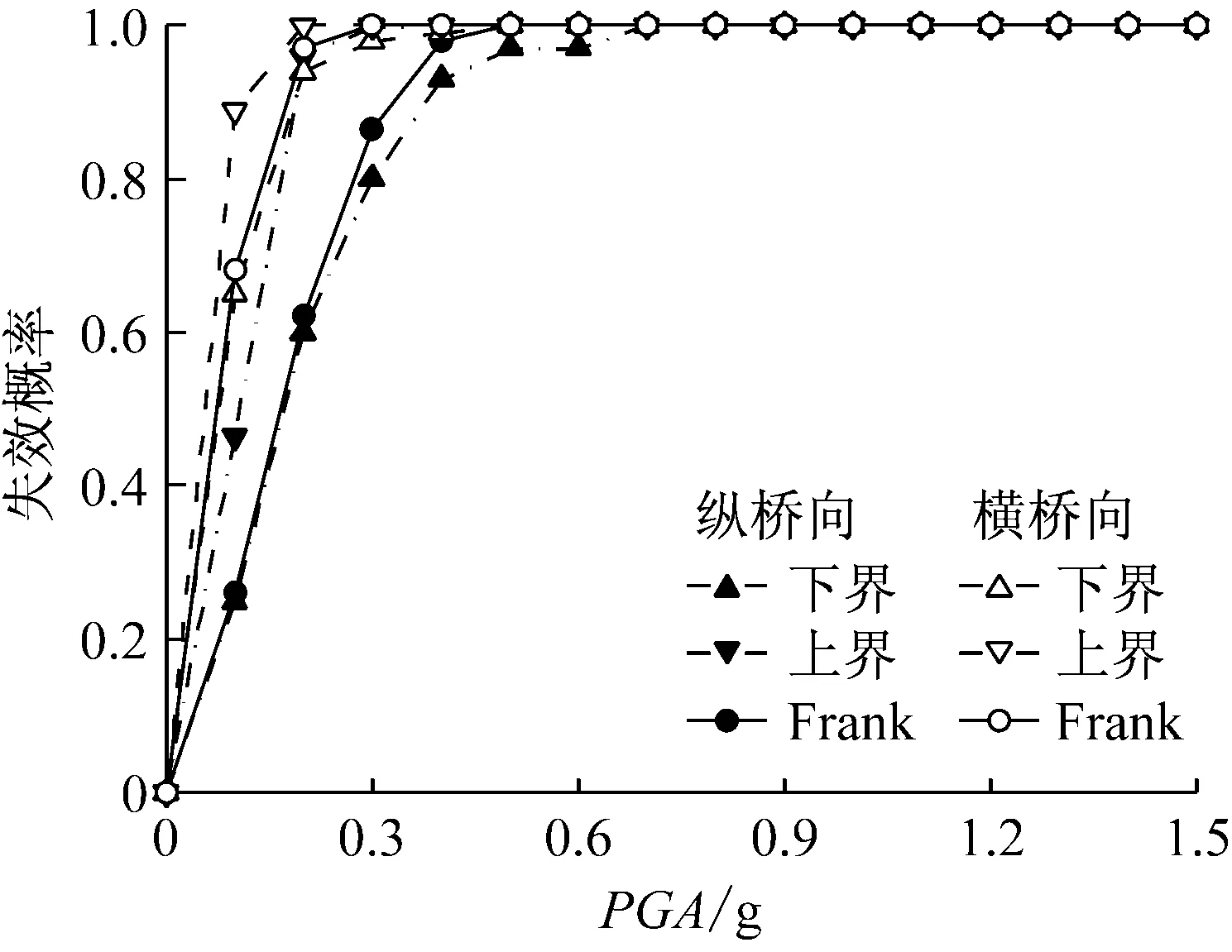
(a) 轻微破坏

(b) 中等破坏

(c) 严重破坏

[1] TASKARI O, SEXTOS A. Multi-angle, multi-damage fragility curves for seismic assessment of bridges[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(7): 2281-2301.

[2] GODA K, TESFAMARIAM S. Multi-variate seismic demand modelling using copulas: application to non-ductile reinforced concrete frame in Victoria, Canada[J]. Structural Safety, 2015, 56:39-51.

[3] 李吉涛,杨庆山,刘阳冰. 多点地震激励下大跨连续钢构桥易损性分析[J]. 振动与冲击, 2013, 32(5): 75-80.

LI Jitao, YANG Qingshan, LIU Yangbing. Fragility analysis of long span continuous rigid frame bridge under multi-support excitations[J]. Journal of Vibration and Shock, 2013, 32(5): 75-80.

[4] 李超,李宏男. 考虑氯离子腐蚀作用的近海桥梁结构全寿命抗震性能评价[J]. 振动与冲击, 2014, 33(11): 70-77.

LI Chao，LI Hongnan． Life-cycle seismic performance evaluation of offshore bridge structures considering chloride ions corrosion effect[J]. Journal of Vibration and Shock, 2014, 33(11): 70-77.

[5] YANG C S W, WERNER S D, DESROCHES R. Seismic fragility analysis of skewed bridges in the central southeastern United States[J]. Engineering Structures, 2015, 83(1): 116-128.

[6] BILLAH A M M, ALAM M S. Seismic fragility assessment of highway bridges: a state-of-the-art review[J]. Structure and Infrastructure Engineering, 2015, 11(6): 804-832.

[7] TAVARES D H, SUESCUN J R, PAULTRE P, et al. Seismic fragility of a highway bridge in Quebec[J]. Journal of Bridge Engineering-ASCE, 2013, 18(15): 1131-1139.

[8] 李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径 RC 连续梁桥系统易损性研究[J]. 土木工程学报, 2012, 45(14): 152-160.

LI Lifeng, WU Wenpeng, HUANG Jiamei, et al. Study on system vulnerability of medium span reinforced concrete continuous girder bridge under earthquake excitation[J]. China Civil Engineering Journal, 2012, 45(14): 152-160.

[9] RAMANATHAN K, PADGETT J E, DESROCHES R. Temporal evolution of seismic fragility curves for concrete box-girder bridges in California[J]. Engineering Structures, 2015, 97: 29-46.

[10] NIELSON B G, DESROCHES R. Seismic fragility methodology for highway bridges using a component level approach[J]. Earthquake Engineering and Structural Dynamics, 2007, 36(6): 823-839.

[11] 董俊,单德山,张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5):845-851.

DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic fragility of irregular continuous rigid frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 845-851.

[12] HONG H P, ZHOU W, ZHANG S, et al. Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components[J]. Reliability Engineering and System Safety, 2014, 121(1): 276-288.

[13] GHOSH S. Modelling bivariate rainfall distribution and generating bivariate correlated rainfall data in neighbouring meteorological subdivisions using copula[J]. Hydrological Processes, 2010, 24(24): 3558-3567.

[14] NELSEN R B. An introduction to Copulas[M]. New York: Springer Science & Business Media, 2013.

[15] 张云, 谭平, 郑建勋, 等. 柱式柔性墩隔震梁桥结构地震易损性分析[J]. 振动与冲击, 2015, 34(16): 48-54.

ZHANG Yun, TAN Ping, ZHENG Jianxun, et al. Seismic fragility analysis on isolated bridges with flexible column piers[J]. Journal of Vibration and Shock, 2015, 34(16): 48-54.

[16] PAROOL N, RAI D. Seismic fragility of multispan simply supported bridge with drop spans and steel bearings[J]. Journal of Bridge Engineering-ASCE, 2015, 20(7):04015021.

[17] RAMADAN M O, MEHANNY S F, ELHOWARY H A. Seismic vulnerability of box girder continuous bridges under spatially variable ground motions[J]. Bulletin of Earthquake Engineering, 2015, 13(6): 1727-1748.

[18] MACKIE K R, CRONIN K J, NIELSON B G. Response sensitivity of highway bridges to randomly oriented multi-component earthquake excitation[J]. Journal of Earthquake Engineering, 2011, 15(6): 850-876.

[19] PAN Y, AGRAWAL A K, GHOSN M, et al. Seismic fragility of multi-span simply supported steel highway bridges in New York State. I: bridge modeling, parametric analysis, and retrofit design[J]. Journal of Bridge Engineering-ASCE, 2010, 15(5):448-461.

[21] 庄卫林,刘振宇,蒋劲松. 汶川大地震公路桥梁震害分析及对策[J]. 岩石力学与工程学报, 2009, 28(7): 1377-1387.

ZHUANG Weilin, LIU Zhenyu, JIANG Jinsong. Earthquake induced damage analysis of highway bridges in Wenchuan earthquake and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1377-1387.

[22] NIELSON B G. Analytical fragility curves for highway bridges in moderate seismic zones[D]. Atlanta: Georgia Institute of Technology, 2005.

[23] NOH H Y, LALLEMANT D, KIREMIDJIAN A S. Development of empirical and analytical fragility functions using kernel smoothing methods[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(12): 1163-1180.

Seismic fragility analysis of a bridge system based on multivariate Copula function

SONG Shuai1, QIAN Yongjiu1, WU Gang2

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Transportation, Southeast University, Nanjing 210096, China)

In order to consider the dependence of piers, bearings and other components’ seismic demands, the multivariate Copula function was adopted to describe the dependence structure of components’ seismic demands and a new method for the seismic fragility analysis of a bridge system was proposed. Based on the results of incremental dynamic analysis, the marginal distribution function of each component was calculated by using the kernel smoothing method. Parameters of the multivariate Copula function were estimated based on the minimum deviation square sum and the optimal Copula function was selected by using the minimum distance method. Combining the component fragility with the multivariate Copula function, the fragility curve of the bridge system was developed and the effects of dependence of components’ seismic demands on the system fragility were analyzed. The results indicated that the dependence of piers, bearings and other components’ seismic demands has an important influence on the seismic fragility of the bridge system; the multivariate Copula function constructed with the minimum deviation square sum can describe the dependence structure of components’ seismic demands accurately and reduce the difficulty level of the bridge system fragility analysis effectively.

bridge system; seismic fragility; multivariate Copula function; dependence of seismic demands; minimum deviation square sum; kernel smoothing method

国家自然科学基金(51178395)

2016-02-02 修改稿收到日期：2016-05-06

宋帅 男，博士生,1987年生

钱永久 男，博士，教授，博士生导师，1963年生

U442.5+5

A

10.13465/j.cnki.jvs.2017.09.019