基于小波和乘法混合核函数LSSVM的顺风向非高斯空间风压预测

迟恩楠， 李春祥， 郑晓芬

(1. 上海大学 土木工程系，上海 200444；2. 同济大学 建筑工程系，上海 200092)

基于小波和乘法混合核函数LSSVM的顺风向非高斯空间风压预测

迟恩楠1， 李春祥1， 郑晓芬2

(1. 上海大学 土木工程系，上海 200444；2. 同济大学 建筑工程系，上海 200092)

提出了基于Marr小波核函数最小二乘支持向量机(Marr-LSSVM)的顺风向非高斯空间风压预测算法。通过传统高斯核函数(RBF)和多项式核函数(Poly)的乘法运算，提出了Poly*RBF-LSSVM(MK-LSSVM)的空间风压预测算法。运用粒子群优化(PSO)算法，对Marr-LSSVM、传统单核CSK-LSSVM和MK-LSSVM的惩罚参数、核函数参数、权重、尺度因子进行优化，建立基于智能优化的非高斯空间风压预测算法；以30 m和50 m处模拟顺风向风压时程作为输入样本，使用提出的预测算法对40 m处风压时程进行了预测。数值分析表明，Marr-LSSVM、MK-LSSVM比CSK-LSSVM具有明显高的非高斯风压预测性能。

预测；顺风向非高斯风压；小波核函数；乘法混合核函数；最小二乘支持向量机；粒子群优化

基于数据驱动技术的样本学习、训练为信号预测提供了一个可行的途径。目前，信号预测主要有时间序列、人工神经网络、支持向量机等方法[1-5]。然而，这些方法都存在理论上或应用上的不足。例如，时问序列方法，高阶模型参数估计难度大、低阶模型预测精度低。人工神经网络作为一种常规的数据驱动算法，具有逼近任意非线性函数的能力，可以映射出序列问题复杂的非线性关系，从而在信号预测中得到广泛应用。然而，传统的人工神经网络存在一些问题：运行时问长，容易陷入局部极小等。支持向量机(Support Vector Machine，SVM)通过核函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻找输入变量和输出变量之间的一种线性关系，解决了“维数灾难”问题。然而，核函数的选择和参数优化决定了SVM的特性。非高斯空间风压数据在高维特征空间分布不平坦，具有尖刺特征。显然，常规(既传统的)的核函数对非高斯空间风压样本的处理可能不合理。为提升非高斯空间风压的预测精度，本文根据小波分析理论，构造出满足Mercer平移不变核定理的小波核函数，建立基于Marr小波核函数最小二乘支持向量机(Marr-LSSVM(Least Squares Support Vector Machines))的非高斯空间风压预测算法；同时，利用Hilbert空间运算的封闭性，通过传统高斯核函数(Radial Basis Function, RBF)和多项式核函数(Poly)的乘法运算，建立基于乘法混合核函数LSSVM(MK-LSSVM)的非高斯空间风压预测算法。

1 最小二乘支持向量机(LSSVM)

给定训练样本集T={(xi,yi)|xi∈Rn,yi∈R,i=1,2,…,l}，Suykens等[6]根据正则化理论改变标准SVM的约束条件和风险函数，即不敏感损失函数被误差的二次平方项代替而作为损失函数，不等式约束条件转变成等式约束条件。因此，LSSVM将求解二次规划问题转化成求解式(1)线性方程组。

s.t.[yi-(ω·Ψ(xi)+b)=ei],i=1,2,3,…,l

(1)

式中：ω为权向量；b为偏置项；C为惩罚参数；ei∈R为误差，e∈Rl×l为误差向量。为解决式(1)的优化问题，构造Lagrange函数

(2)

对式(2)求偏导，并根据最优化理论中的KKT(Karush-Kuhn-Tucher)条件，得到式(3)和约束条件

(3)

设α=[α1,α2,…，αl]T，Q=[1,1,…,1]T，Y=[y1,y2,…,yl]T，I为单位矩阵。联立求解方程组，消去ω和ei，则式(3)的解为

(4)

最后，得到LSSVM的回归模型

(5)

式中，K为核函数矩阵，其中元素k(xi,xj)=Ψ(xi)×Ψ(xj)。

2 LSSVM的核函数及发展

由式(5)可知，核函数是支持向量机的核心。核函数的引入巧妙地避开了高维空间数学运算复杂度的问题，使得支持向量机可以在较少的样本下有效地处理高维问题。

传统的单一核函数(Conventional Single Kernel, CSK)。核函数研究表明，对于特定的核函数，在给定样本集中的任意一个样本都可能成为一个支持向量。这就意味着在一个核函数下观察到的特征在其它核函数下并不能保持[7]。因此，对解决具体问题来说，选择合适的核函数是非常重要的。核函数在数学上必须满足Mercer条件，传统的核函数分为两大类：局部核和全局核[8-9]。局部核的二维图形表现为钟形特征，即当输入向量x和y相距较远时，对应的核估计值将变得非常小甚至为0，具有很好的局部学习能力，插值能力较强，例如高斯核函数(RBF)

(6)

式中，σ为RBF核宽度。

全局核考虑所有输入样本数据在特征空间的点积作用，因此它有着良好的全局性质，泛化能力出众，例如多项式核函数(Poly)

KPoly(x,y)=[(x·y)+1]q

(7)

式中，q为Poly核阶数。

单一小波核函数(Wavelet Kernel, WK)。根据小波分析理论，对母小波函数h(x)进行伸缩和平移，可以得到与母小波相似的副本[10-11]，即

(8)

式中：a为尺度因子；b为平移因子。

根据式(8)构造满足Mercer平移不变核定理小波核函数，即平移不变核函数K(x,y)=K(x-y)是一个允许支持向量核，当且仅当K(x)的傅里叶变换

(9)

则由该函数生成的Mercer平移不变核函数为

(10)

选定常用的母小波有：Marr小波函数

(11)

为证明满足Mercer平移不变核定理，将式(11)代入式(9)可得到

(12)

则对于所有ω均有式(13)的F[k](ω)≥0，所以Marr小波核函数为支持向量机允许核函数。将式(11)代入式(10)可生成Mercer平移不变核的Marr小波核函数

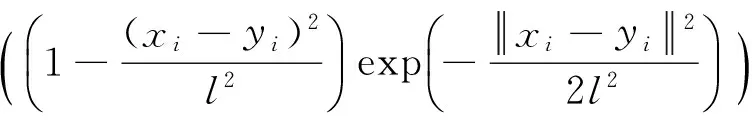
(13)

乘法混合核函数(Multiplicative Mixed Kernel, MK)。支持向量机核函数是在完备的内积空间定义的，其在希尔伯特空间的乘积运算属于封闭运算，其结果仍属于希尔伯特空间[12-13]。根据Mercer条件，设K1和K2是χ×χ(χ⊂Rn)上的核函数，则式(14)对核函数的混合仍为支持向量机允许核函数。

K(x,y)=K1(x,y)·K2(x,y)

(14)

根据式(13)和式(14)，结合局部核RBF和全局核Poly两种核函数的优势，构造混合核函数，使其兼具局部核函数和全局核函数的特征，以此提高学习精度。混合核函数具体构造为

Poly*RBF组合

(15)

式中，a为核权重系数，a∈[0,1]。

由式(15)所建立的多核混合矩阵为对称矩阵，具有下列性质。

(16)

综上，本文根据小波分析理论，建立了满足Mercer平移不变核定理的Marr小波核函数KMarr；为改进传统单核CSK-LSSVM预测精度不高的缺陷，构造基于乘法运算的混合核函数K*。

3 非高斯空间风压的预测算法

将顺风向非高斯风压样本进行归一化处理后，输入到核函数中，形成核函数矩阵，即将非高斯风压样本映射到高维特征空间。在特征空间，对核函数矩阵实施各种线性算法，以建立顺风向非高斯风压的预测算法。根据上述核函数，表1给出了SK-LSSVM和MK-LSSVM的非高斯风压预测算。

表1 SK-LSSVM和MK-LSSVM非高斯风压预测算法

Fig.1 SK-LSSVM and MK-LSSVM algorithms for the prediction of non-Gaussian wind pressure

模型核函数形成方式核函数表达式SK-LSSVM(单核)CSK-LSSVM(传统单核)RBFPoly式(6)式(7)Marr-LSSVM(小波核)Marr式(13)MK-LSSVM(混合核)Poly*RBF-LSSVM(乘法混合)式(15)

采用PSO优化算法，对表1中的SK-LSSVM和MK-LSSVM参数进行优化，以建立PSO-CSK-LSSVM、PSO-WLSSVM(PSO-Marr-WLSSVM)和PSO-MK-LSSVM(PSO-Poly*RBF-LSSVM)预测算法。图1给出了非高斯空间风压预测算法流程。

图1 顺风向非高斯空间风压预测算法的流程

Fig.1 Flowchart of algorithms for the prediction of non-Gaussian spatial along-wind pressure

4 预测算法的数值验证

考虑某160 m高的超高层建筑，每隔10 m选为非高斯风压模拟点，以获得不同高度处的非高斯风压时程，本文仅考虑顺风向风荷载。脉动风速谱采用Kaimal谱，脉动风速互功率谱为

(17)

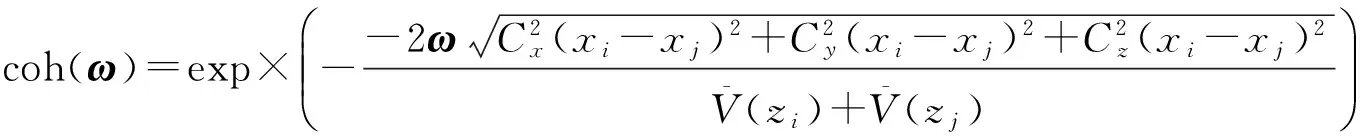
在顺风向风荷载作用下，根据“准定常”理论设风压目标边缘概率分布函数为对数正态分布，则风压目标功率谱函数为

(18)

根据上述风速风压公式和表2的相关模拟参数，采用无记忆非线性转换方法[14-15]模拟生成30 m和50 m处1 000 s顺风向非高斯风压样本，如图2所示。

表2 数值模拟参数

(a) h=30 m

基于智能优化SK-LSSVM和MK-LSSVM的非高斯风压预测步骤如下：

步骤1 设30 m和50 m处的风压时程为输入样本，而40 m处的风压时程作为输出。将1 000 s的非高斯风压样本数据分成两部分：前500 s的风压数据作为学习训练样本，后500 s的风压数据作为预测验证样本。对40 m处的后500 s非高斯风压进行预测。

步骤2 设PSO粒子种群规模M=30，迭代次数K=150，随机产生粒子初始位置和初始速度，确定核函数待优化参数的取值范围，如表3所示。其中，对Poly核，取q=3以达到全局拟合能力与计算时间的折衷。

表3 核参数的取值范围

步骤3 输入训练样本数据，利用核函数将非高斯风压样本映射到高维特征空间，建立LSSVM预测算法。计算每个粒子的适应度，通过粒子自身适应度与自身最佳适应度值和群体最优适应度值的比较，不断地更新粒子的速度和位置，获得最优参数，从而建立基于表1中4种核函数的最优LSSVM算法。于是，对后500 s采样时间点的非高斯风压进行预测。

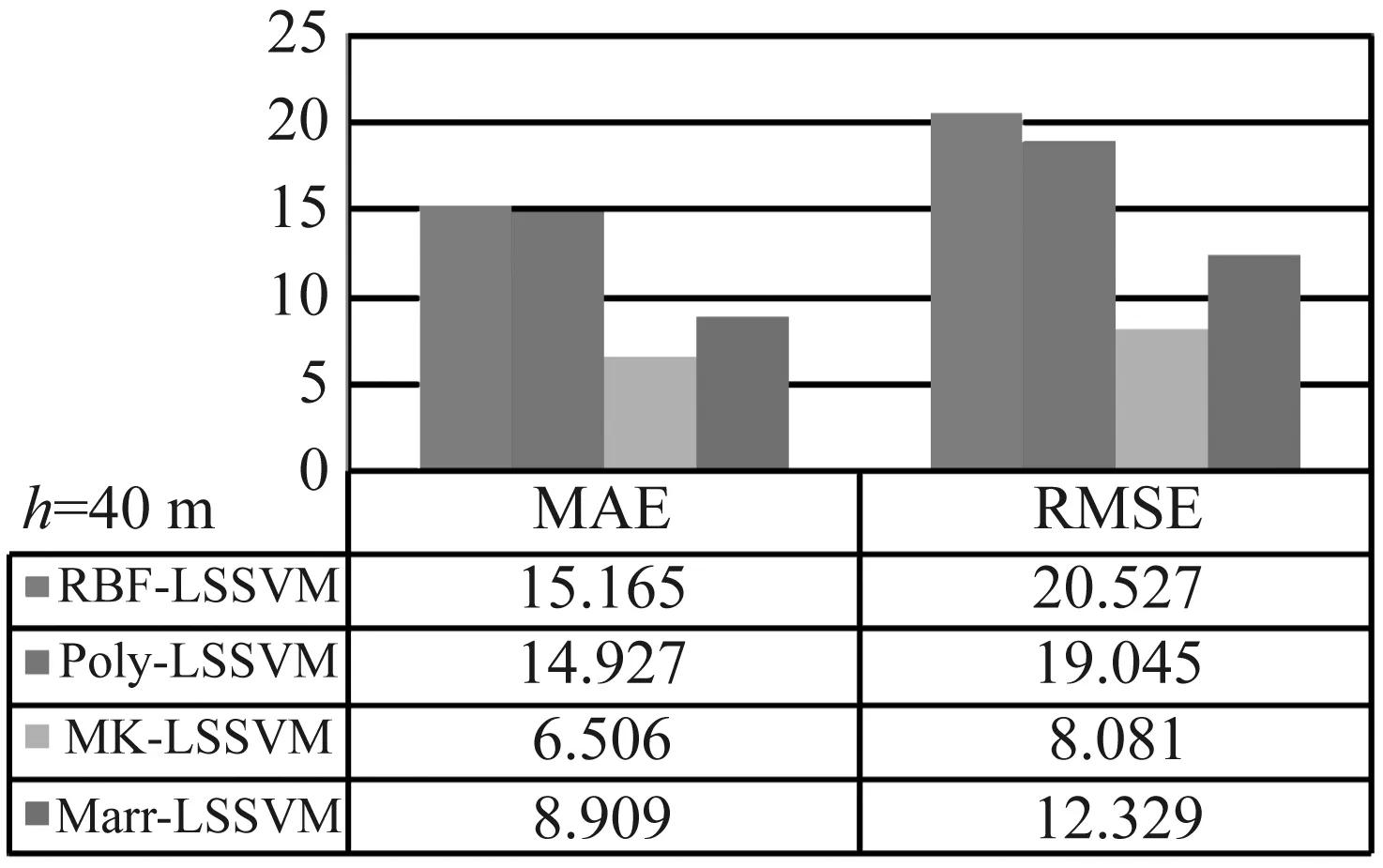
使用提出的Marr-WLSSVM和MK-LSSVM算法对40 m处的后500 s非高斯风压进行预测，同时给出CSK-LSSVM(包括RBF-LSSVM和Poly-LSSVM)的预测结果作为对比。非高斯风压时程的预测值，如图3所示，自相关函数的对比，如图4所示；训练集和预测集的评价指标对比，如图5所示；训练集和预测集的偏度、峰度对比如表4和表5所示。

(a)

(b)

从这些结果可看出，核函数的选取对LSSVM预测效果有较大的影响。无论是训练集还是预测集，CSK-LSSVM的风压预测结果精度较差；特别，从预测风压的自相关函数(见图4)看，CSK-LSSVM的结果与模拟值拟合较差，存在很大的误差。根据评价指标(见图5)，无论是训练集还是预测集，MK-LSSVM和Marr-LSSVM的MAE和RMSE比CSK-LSSVM的下降很多。以预测集的风压为例，MK-LSSVM较RBF-LSSVM的MAE由15.165降为6.506，RMSE由20.527降为8.081，误差下降幅度分别为57%和60%；Marr-LSSVM也是如此。同时，虽然预测集风压的相关系数R=0.904(RBF-LSSVM)、R=0.920(Poly-LSSVM)都达到0.9以上，但与MK-LSSVM(R=0.986)和Marr-LSSVM(R=0.967)相比，其精度依然有待提高。其主要原因是：RBF核有局部性，学习能力很强但泛化能力较弱，导致其预测结果误差很大；而Poly核为全局核，虽然有较强的泛化能力，但是对数据信号的局部分析能力较弱，不能满足预测完整风压时程精度的要求。

(a)

(b)

Fig.4 Autocorrelation functions, respectively, corresponding to predicted and simulated wind pressure time histories at 40 m

(a) 训练集

(b) 测试集

Fig.5 Prediction performance index for training and testing data set(at 40 m)

非高斯风压的最显著特征是高阶矩，即偏度(三阶)和峰度(四阶)。表4给出了训练集中模拟风压的偏度为0.929、峰度为4.498，而4种核函数的训练集结果呈现：MK-LSSVM和Marr-LSSVM的训练集结果与模拟风压的非常接近。表5给出预测集中模拟风压的偏度为0.98、峰度为4.925，而4种核函数的预测集结果显示：MK-LSSVM和Marr-LSSVM的预测集结果与模拟风压能较好吻合。偏度和峰度的比较再次表明MK-LSSVM和Marr-LSSVM的预测精度更好。这主要是由于MK核利用Hilbert空间乘法运算的包闭性质，融合了RBF与Poly的优点，既具有很强的学习能力也同时具备了强的泛化能力；而Marr小波核函数具有稀疏变化和尺度分析性质，能够提升预测算法的精度。

表4 40 m处训练集风压和模拟风压的峰度和偏度

Fig.4 Kurtosis and skewness, respectively, corresponding to training data set and simulated wind pressure time histories at 40 m

指标模拟风压RBF-LSSVMPoly-LSSVMMK-LSSVMMarr-LSSVM峰度4.4983.5634.2804.6124.597偏度0.9290.8240.8810.9600.928

表5 40 m处预测集风压和模拟风压的峰度和偏度

Fig.5 Kurtosis and skewness, respectively, corresponding to testing data set and simulated wind pressure time histories at 40 m

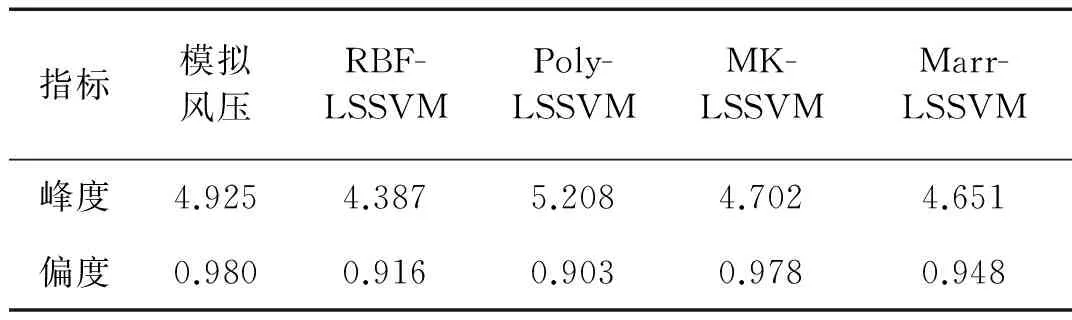
指标模拟风压RBF-LSSVMPoly-LSSVMMK-LSSVMMarr-LSSVM峰度4.9254.3875.2084.7024.651偏度0.9800.9160.9030.9780.948

5 结 论

提出了Marr-LSSVM和MK-LSSVM的顺风向非高斯空间风压预测算法。数值结果表明，Marr-LSSVM核函数具有小波的局部化、多层次的优点，其预测精度相较于CSK-LSSVM有很大的提升，可以作为机器学习的一种新的有效单核函数。MK-LSSVM能够在RBF核函数的作用下有具有很好的学习能力(训练误差小)，同时也在Poly核函数的作用下有很强的泛化能力(测试误差小)，从而使预测误差较Marr-LSSVM进一步下降，预测性进一步提升。因此，提出的Marr-LSSVM和MK-LSSVM能够为结构风工程设计和分析提供完整可靠的空间风压时程，具有较高的工程应用价值。

[1] 张华，曾杰. 基于支持向量机的风速预测模型研究[J]. 太阳能学报，2010, 31(7): 928-931.

ZHANG Hua, ZENG Jie. Research on wind speed forecasting model based on support vector machine[J]. Journal of Solar Energy, 2010, 31(7): 928-931.

[2] 张广明，袁宇浩，龚松建. 基于改进最小二乘支持向量机方法的短期风速预测[J]. 上海交通大学报，2011, 45(8): 1125-1129.

ZHANG Guangming, YUAN Yuhao, GONG Songjian. Short term wind speed forecasting based on improved least square support vector machine method[J]. Journal of Shanghai Jiao Tong University, 2011, 45(8): 1125-1129.

[3] QU Wenglong，FAN Guangquan，YANG Bingru. Research on complicated time series prediction based on support vector machines[J]. Computer Engineering，2005, 23(12): 1-2.

[4] RAJASEKARAN S, GAYATHRI S, LEE T L. Support vector regression methodology for storm surge predictions[J]. Ocean Engineering，2008, 35(16): 1578-1587.

[5] CHEN T T, LEE S J. A weighted LS-SVM based learning system for time series forecasting[J]. Information Science, 2015, 299: 99-116.

[6] SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.

[7] ZHANG Yin, DAI Miaolin, JU Zhimin. Preliminary discussion regarding SVM kernel function selection in the twofold rock slope prediction model[J]. Computing in Civil Engineering, 2015, 30(3): 04015031.

[8] CHEN W J, WANG J. Application of support vector machine in industrial process[J]. Computers and Applied Chemistry, 2005, 22: 195-200.

[9] 赵晨晖. 基于混合和函数支持向量机的基金投资决策研究[D]. 广东：华南理工大学，2012.

[10] NOURISOLA H, AHMADI B. Robust adaptive H∞controller based on GA-Wavelet-SVM for nonlinear vehicle suspension with time delay actuator[J]. Journal of Vibration and Control, 2015, 10:1-10.

[11] 李坤，谭梦羽. 基于小波支持向量机回归的股票预测[J]. 统计与决策，2014(6)：32-36.

LI Kun, TAN Mengyu. Stock forecasting based on wavelet support vector machine regression[J]. Statistics and Decision Making, 2014(6): 32-36.

[12] CHEN Fafa，TANG Baoping，SONG Tao，et al. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization[J]. Measurement，2014, 47(1): 576-590.

[13] WU Peng, DUAN Fuqing, GUO Ping. A pre-selecting base kernel method in multiple kernel learning[J]. Neurocomputing, 2015, 165: 47-52.

[14] 罗俊杰，苏成，韩大建. 高斯/非高斯混和随机风压场的模拟方法[J]. 振动与冲击，2012，31(10)： 111-117.

LUO Junjie, SU Cheng, HAN Dajian. Simulation methodology for stochastic wind pressure field composed of gaussian and non-gaussian regions[J]. Journal of Vibration and Shock, 2012, 31(10): 111-117.

[15] 李锦华. 非高斯随机过程模拟算法研究[D]. 上海：上海大学, 2010.

Forecasting non-Gaussian spatial along-wind pressure using wavelet kernel and multiplicative mixed kernel functions based LSSVM

CHI Ennan1, LI Chunxiang1, ZHENG Xiaofen2

(1. Department of Civil Engineering, Shanghai University, Shanghai 200444, China; 2. Department of Structural Engineering, Tongji University, Shanghai 200092, China)

Here, Marr wavelet kernel-based least squares support vector machines (LSSVM) referred to as Marr-LSSVM, was proposed to predict along-wind non-Gaussian spatial wind pressure. Through multiplication operation of the conventional radial basis function (RBF) kernel and polynomial kernel, Poly*RBF-LSSVM was then proposed, it was called the multiplicative mixed kernel MK-LSSVM. By using the particle swarm optimization (PSO) algorithm, optimizations were implemented for penalty parameters, kernel parameters, weights, and scale factors of Marr-LSSVM, conventional single kernel CSK-LSSVM, and MK-LSSVM, thus the non-Gaussian spatial wind pressure forecasting algorithms were built based on intelligent optimization. The simulated along-wind pressures at 30 m and 50 m were taken as input samples, the wind pressure at 40 m was then predicted using the proposed algorithms. The numerical analyses demonstrated that Marr-LSSVM and MK-LSSVM can provide an obvious higher performance to predict the non-Gaussian spatial wind pressure than CSK-LSSVM can.

forecasting; non-Gaussian spatial along-wind pressure; wavelet kernel functions; multiplicative mixed kernel functions; least squares support vector machines; particle swarm optimization

国家自然科学基金(51378304)

2015-12-22 修改稿收到日期：2016-03-01

迟恩楠 男，硕士生，1989年生

郑晓芬 女，博士，讲师，1963年生

TU311

A

10.13465/j.cnki.jvs.2017.09.018