一种绳牵引摄像机器人的运动控制策略与稳定性研究

韦慧玲， 仇原鹰， 盛 英

(西安电子科技大学 电子装备结构设计教育部重点实验室， 西安 710071)

一种绳牵引摄像机器人的运动控制策略与稳定性研究

韦慧玲， 仇原鹰， 盛 英

(西安电子科技大学 电子装备结构设计教育部重点实验室， 西安 710071)

绳牵引摄像机器人具有索单向受力、冗余驱动以及高速机动等特性，因而其稳定性问题的研究与解决是一个难题。现有的研究中，大多没有考虑摄像机器人的高速稳定运动特性及控制方法。为此，提出一种基于末端位置空间PD修正前馈控制规则保证摄像机器人的稳定运行。通过牛顿-欧拉法建立了末端执行器的动力学方程以及驱动系统的动力学模型；在此基础上得到了整个系统的动力学模型；在系统动力学模型的基础上，提出基于末端位置空间PD修正前馈控制规则的绳牵引摄像机器人跟踪控制策略，通过Lyapunov稳定性理论论证了控制策略的稳定性；通过数值算例说明了摄像机器人的稳定跟踪性能，并且验证了控制策略的有效性。

摄像机器人；动力学；控制策略；李雅普诺夫稳定性；跟踪控制

相对于杆支撑的并联机器人，绳牵引并联机器人具有结构简单、质量轻、运动链惯性小、工作空间大、承载能力大、运动速度快、累积误差小、干涉发生几率小以及可拆装重组等优点。在应用中，对绳牵引并联机器人有各种不同的功能和性能要求。为此，人们从不同的领域对之开展了研究(如静力学、动力学、运动学、机构性能分析、控制理论等)[1-5]，从不同的角度定义了一系列不同的性能评价指标(如工作空间、奇异性、刚度分析、驱动力求解、精度误差等)[6-10]，并提出了各种分析计算理论和方法，来指导绳牵引并联机器人的开发研究与应用实践。绳牵引并联机器人由于柔索承载的单向性，在系统的高速、高精度运行方面面临着更多的挑战性问题，其中稳定性显得尤为重要。

目前，有一些研究人员从不同的角度对绳牵引并联机器人的稳定性进行了研究，并取得了一些成果。文献[11]研究了欠约束的绳牵引并联机器人基于斜率的稳定性测量方法。但该方法是否适用于完全约束的绳牵引并联机器人有待探讨。文献[12-13] 把一根绳索等效为四个没有预紧力的弹簧建立了绳牵引并联机器人的刚度模型。分析了刚度矩阵与机构的稳定性关系，证明了刚度矩阵的正定与系统稳定性的充分必要条件。通过平面的绳牵引并联机器人进行数值仿真，没有运用空间的并联机器人进行仿真。而且，4个弹簧的刚度代替一根绳索的刚度在矩阵形式上有区别，它们的近似程度需要商榷。文献[14] 考虑绳索弹性和下垂建立了基于绳索弹性悬链线模型的刚度矩阵模型。提出了一种以四元数为基础的刚度矩阵，分析了刚度与系统稳定性间的关系。文献[15-16]根据Hessian矩阵对应用在直升机吊装上的绳牵引并联机器人的所有平衡构型的稳定性进行了分析，其认为只要Hessian矩阵是正定的，那么该构型就是稳定的。文献[17]针对绳牵引并联起重机的静态平衡点的稳定性进行评估。根据几何约束条件推导出Hessian矩阵，并分析了矩阵的所有特征值为正是平衡构型为稳定性的充要条件。文献[18]基于最小索拉力以及拉力最小的绳索与水平面夹角正切值分析了绳牵引摄像机器人的稳定性。以上的文献成果都只是分析了系统的结构稳定性，并没涉及到运动稳定性的分析。文献[19] 通过矢量封闭原理以及李雅普诺夫稳定性理论分析了基于绳长坐标的PD反馈控制的运动稳定性。但其控制策略对反馈量没有进行修正,故会引起较大的误差。文献[20]基于李雅普诺夫稳定性理论设计了绳牵引机器人正输入线性反馈控制器，通过实验证明了该控制律的有效性。但未说明该方法是否适用于高速运动的绳牵引并联机器人。文献[21]提出一种基于不确定雅可比矩阵的鲁棒PD控制，运用李雅普诺夫函数证明了该控制律的渐进稳定性。但该控制方法只使用在失重状态下。文献[22]提出一种基于李雅普诺夫函数的反馈控制技术，在正输入约束条件下可以达到目标位置的渐近稳定。但该技术只适用于平面的绳牵引并联机器人。文献[23]针对冗余约束的绳索驱动的并联机器人提出一种综合的控制单元，并运用李雅普诺夫稳定性理论分析了闭环系统的渐进稳定性。该控制律没有将绳索长度误差进行反馈，因此跟踪精度不高，此外，该方法只针对冗余约束的绳牵引并联机器人。文献[24-25]针对平面绳牵引并联机器人KNTU提出了鲁棒控制算法，并应用李雅普诺夫第二方法证明了其运动稳定性。但其算法是否适用于空间高速运动的绳牵引并联机器人有待探讨。尽管上述文献都对绳牵引并联机器人提出了控制律以及应用李雅普诺夫稳定性理论证明了控制算法的稳定性，但并不适用在做高速机动运动的冗余驱动的绳牵引并联机器人。

文中以绳牵引并联机器人为研究对象，通过建立末端执行器的动力学模型和驱动系统的动力学方程，构建绳牵引并联机器人系统的动力学模型。基于该模型，根据系统的绳索单向受力特性、冗余驱动性以及高速机动运动特性，提出基于末端位置空间PD修正前馈控制规则的绳牵引摄像机器人跟踪控制策略并运用李雅普诺夫运动稳定性理论研究控制策略的运动稳定性。

1 动力学分析

1.1 末端执行器的动力学模型

为了建立绳牵引并联机器人的动力学模型描述其高速机动运动和绳索单向受力特性，本文做了以下一些假设：绳索与机架、末端执行器的连接为理想铰接；绳索满足理想柔性的条件，既不能受压，也不能受弯；绳索的变形符合胡克定律。

如图1(a)所示，建立与大地固连的全局坐标系O-XYZ和与固结与末端执行器质心的局部坐标系P-xyz，从局部坐标系到全局坐标系的旋转变化矩阵为op。pAi为局部坐标系P-xyz中绳与末端执行器铰接点Ai的位置矢量。图1(b)为5 m原理样机模型，4台伺服电机分布在4个索支撑杆的下部，4个滑轮分布在4个索支撑杆的上部。4条柔索绕过滑轮在伺服系统的驱动下可实现收放运动，从而牵引着摄像机在工作空间内运动。对于由m根绳牵引的n自由度完全约束绳牵引并联机器人(m=n+1)，利用牛顿-欧拉法，推导出末端执行器的动力学方程

(1)

式(1)也可表达为

(2)

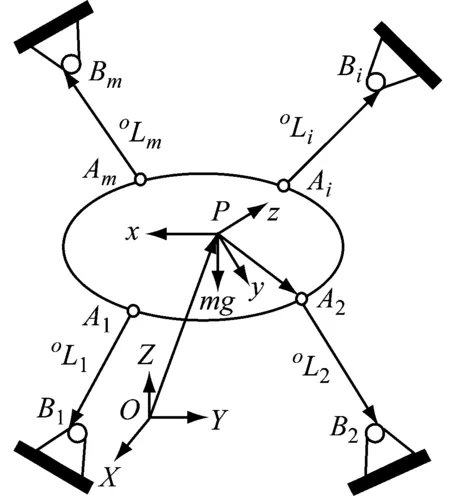
(a) 完全约束绳牵引并联机器人动力学示意图

(b) 5 m原理样机模型

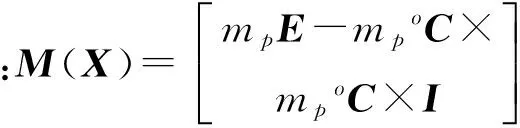
式(2)可表达为

(3)

式中，G(X)为力相关矩阵。

至此，就得到了末端执行器的动力学模型的矩阵形式。

1.2 驱动器的动力学模型

绳牵引并联机器人的驱动器包括电机、减速器以及绞盘。驱动器的动力学方程可以表示为

(4)

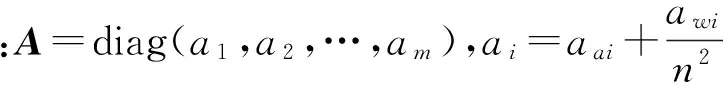
1.3 系统的动力学模型

当电机转角为θ时会引起绳索的长度变化量为ΔL，因此有绳长与电机转角的关系式为

rθ=ΔL=(L-L0)

θ=r-1(L-L0)

(5)

通过对式(5)进行微分得

(6)

联立式(3)、式(4)、式(6)得到系统的动力学模型如下

(7)

进一步整理得

(8)

其中，

(9)

2 轨迹跟踪控制策略

完全约束的绳牵引并联机器人是高度耦合的非线性系统，并且是冗余驱动，因此在设计控制方案时，需要对动力学模型进行线性化和解耦处理，并通过索力优化分配解决冗余驱动带来的索力不确定性。控制规则参考文献[26]提出的PD修正前馈控制规则，如图2所示。假设期望的位姿为Xd，PD修正前馈控制规则的控制律为

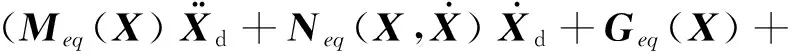
(10)

式中：Κp、Kd为反馈增益矩阵；J†为JT的广义逆，J†=J(JTJ)-1；e=Xd-X是误差；Q为JT的零基底空间向量，满足关系

JTQ=0

(11)

Q的作用是在绳子间产生内力保证绳子时刻处于张紧状态。

把式(10)代入式(8)，并联立式(11)，移项整理后得到如下的闭环系统

(12)

图2 控制策略示意图

3 基于Lyapunov理论的稳定性分析

3.1 Lyapunov稳定性理论

稳定性是一个系统正常运行的前提条件。根据李雅普诺夫的稳定性理论[27]，设连续时间非线性时变系统的状态方程为

(13)

式中：x为n维状态向量；t为时间变量；f(x,t)为n维函数，其展开式为

(14)

假定方程的解为x(t;x0,t0),x0和t0分别为初始状态向量和初始时刻，x(t0;x0,t0)=x0。

平衡状态

(15)

定理 (李雅普诺夫稳定性定理) 对于定常系统式(14)，若存在一个具有连续一阶导数的标量函数V(x,t)，V(0,t)=0，并且对于状态空间X中的一切非零x满足以下条件：

(1)V(x,t)是具有连续一阶偏导数的正定函数；

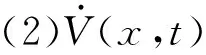
由此，假设非线性时变系统的二次型标量函数为

V(x,t)=xTPx

(16)

式中：P为待定的对称正定矩阵。根据李雅普诺夫稳定性理论可知，式(14)渐进稳定的充要条件是李雅普诺夫函数式(16)对时间的导数为负定，即

(17)

3.2 稳定性分析

本节证明绳牵引并联摄像机器人控制策略的稳定性。首先对闭环系统式(12)建立李雅普诺夫标量函数V。根据系统的总能量构造如下的李雅普诺夫函数[28]

(18)

对李雅普诺夫函数式(18)沿着对时间的全导数表示为

(19)

把式(12)代入式(19)，得

(20)

根据机器人动力学方程可知，非线性机器人系统具有如下的结构特性[29]

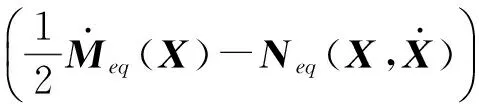
(21)

因此，式(20)简化为

(22)

由于Kd是正定的，故有

(23)

3.3 一致连续性证明

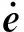
(24)

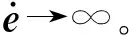
4 数值仿真

4.1 仿真参数设置

为了验证控制策略的有效性进行了数值仿真。摄像机器人是由4根绳索牵引3平动自由度的完全约束冗余驱动系统。以场地中心处为全局坐标系原点，摄像机器人有关仿真参数如下：1#滑轮位置坐标为B1=[-19.5 21 25]Tm，2#滑轮位置坐标为B2=[19.5 21 25]T，3#滑轮位置坐标为B3=[19.5 -21 25]Tm，4#滑轮位置坐标为B4=[-19.5 -21 25]Tm。末端执行器动平台质量为mp=20 kg；绳索参数参考《钢丝绳手册》，公称直径为r=3 mm，单位长度质量为m0=0.045 6 kg/m，弹性模量为E=2.8×104MPa，最小破断拉力为Tmax=3 000 N，选定的最小预紧力为Tmin=10 N,黏性阻尼系数为c=0.2。驱动单元中电机的额定输出力矩τmax=15.8 N·m ，τmin=-15.8 N·m，等效到电机轴的转动惯量7.52×10-4kg·m2，等效黏性阻尼系数1.88×10-4N·m·s，减速比n=4∶1，绞盘半径rw,i=0.04 m。仿真过程中，运行时间为t=10 s，微分方程的数值求解采用四阶龙格-库塔方法。控制参数Kp和Kd根据临界比例法和现场调试确定。

(25)

4.2 仿真结果与分析

不同运动速度下沿着空间螺旋线轨迹的位置跟踪误差，如图3所示。其中图3(a)为速度为v=9.44 m/s的超高速运动，图3(b)为速度为v=6.31 m/s的高速运动，图3(c)为速度为v=3.20 m/s的中速运动，图3(d)为速度为v=0.89 m/s的低速运动。由图3可知，由于绳索纵向抖动的原因，前2 s内Z方向有稍微的跳动。由于Z方向是做匀速上升运动，因此其误差来源除了纵向绳索抖动外，还有跟踪运动产生的跟踪误差，但随着运动进入平稳状态，误差逐渐接近于可接受范围。速度越大，位置跟踪误差越大，Z方向上启动抖动更明显。原因在于速度越大，末端执行器突然启动需要绳索提供更大的张力才能够满足跟踪效果，引起了跳动。由图3还可知，当速度增大时，跟踪误差明显随着变大，这是因为速度越大，末端执行器惯性引起的振动越大，故引起更大的误差。因此，如何抑制绳索纵向振动是今后研究的一个重要方向。

(a) 超高速运动v=9.44 m/s

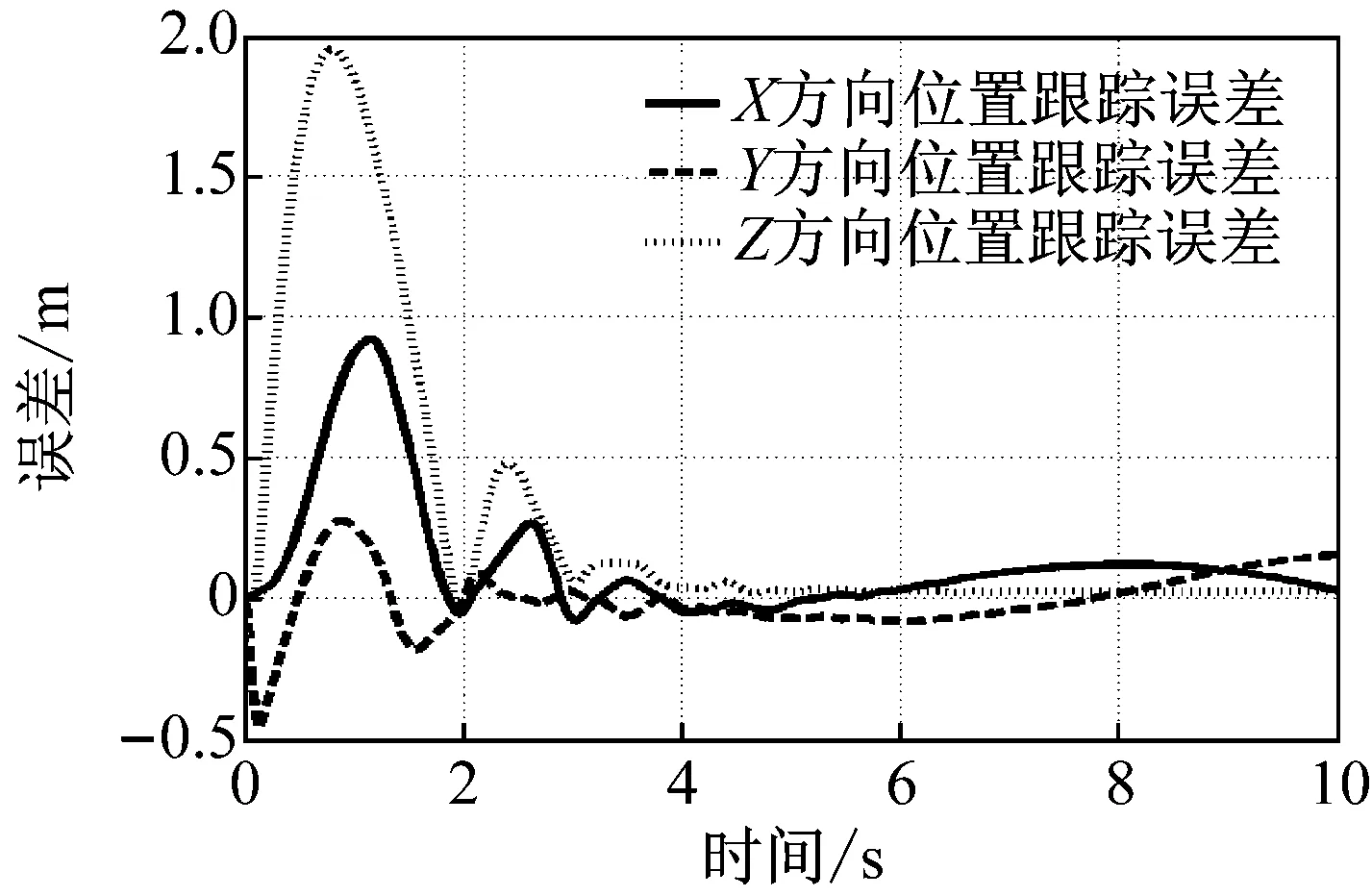
(b) 高速运动v=6.31 m/s

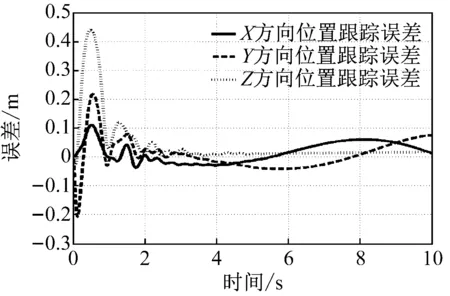
(c) 中速运动v=3.20 m/s

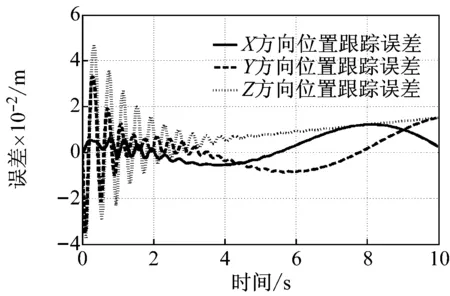
(d) 低速运动v=0.89 m/s

不同运动速度下沿着空间螺旋线轨迹的速度跟踪响应误差，如图4所示。由图可知中低速时PD修正前馈控制策略的速度响应时间在2 s内，2 s后速度跟踪误差收敛，跟踪速度达到期望值，末端执行器稳定运行。高速运行时，由于绳索抖动加剧，速度响应时间达到4 s，但后6 s速度跟踪误差逐渐收敛，最终进入平稳运行状态。由图4可知速度误差最终收敛，即控制输入速度是全局有界，满足绳牵引并联机器人轨迹跟踪控制要求。

(a) 超高速运动v=9.44 m/s

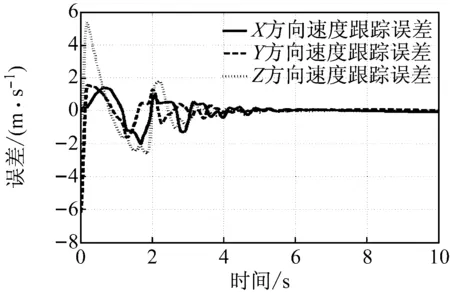
(b) 高速运动v=6.31 m/s

(c) 中速运动v=3.20 m/s

(d) 低速运动v=0.89 m/s

图5所示的是不同运动速度下沿着空间螺旋线轨迹的索力变化情况。由图5可知，索力光滑连续变化，符合期望要求。随着速度的增加，四索索力增加。这是因为螺旋线轨迹的半径增大，向心加速度变大，因此需要的向心力变大，故绳索提供的张力变大。随着末端执行器高度的不断上升，柔索的张力也逐渐增大，故图5中张力曲线呈周期上升趋势。由图5(a)可知，末端执行器进行超高速跟踪时，绳索存在虚牵现象，即索张力为0，跟踪运动不可实现的，此时速度是9.44 m/s，这比目前著名的摄像机器人SpiderCam的最高速度9 m/s还要大[31]。故解决超高速运动时绳索的虚牵问题是进一步要展开的工作。但总体上跟踪过程中索力的变化是连续稳定的，故控制器的设计是合理的。

(a) 超高速运动v=9.44 m/s

(b) 高速运动v=6.31 m/s

(c) 中速运动v=3.20 m/s

(d) 低速运动v=0.89 m/s

图6所示的是摄像机器人在高速和低速稳态运行过程中绳索的索长误差量。由图6可知，高速运行时索长的误差量比低速时在数量级上大了将近100倍。说明高速运行时绳索抖动幅度比低速时要大。低速运行时，控制系统需要4 s时间进行索长误差量调整适应，4 s后调整完成，绳索长度变化趋向光滑，末端执行器进入平稳运行状态。

(a) 高速运动v=6.31 m/s

(b) 低速运动v=0.89 m/s

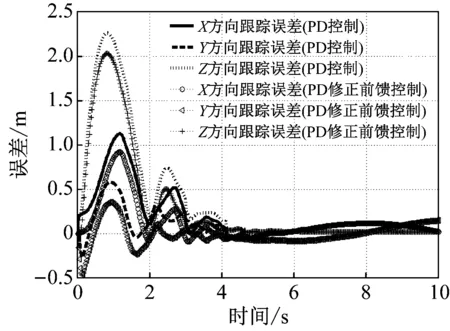
(a) 高速运动v=6.31 m/s

(b) 低速运动v=0.89 m/s

末端执行器运行速度与最大位置跟踪误差的关系如图8所示。由图8可知，Z方向上误差随着速度的增加而呈现指数增加，说明了速度增大后绳索纵向抖动加剧导致末端执行器偏离规划轨迹的幅度越来越大。

图8 速度与最大位置跟踪误差关系

图9 速度与最小索力关系

5 结 论

(1) 针对绳索单向受力特性的绳牵引并联机构的特点，分别建立基于牛顿-欧拉法的末端执行器动力学模型和驱动系统的动力学模型，进一步得到机器人的动力学模型。

(2) 针对绳索受力单向性、高速机动性以及冗余驱动等特点，以轨迹控制为目标，设计了基于末端位置空间PD修正前馈控制策略。基于Lyapunov稳定性理论证明了控制策略的稳定性和一致连续性。

(3) 以4索牵引的3 自由度并联冗余驱动摄像机跟踪空间螺旋线运动为例，验证了建模方法和控制策略设计的稳定性。位置跟踪误差和速度响应误差都能快速收敛，达到了比较高精度的跟踪效果。表明在所设计的控制策略作用下，系统在低速、中速、高速状态可以平稳、光滑、有界地实现轨迹跟踪。

(4) 为解决系统超高速运行的失稳现象，下一步需要解决绳索的虚牵问题。针对突然启动时绳索抖动问题，需要对启动的运动进行高次插值规划，这也是今后研究的内容。

[1] DINH Q N, MARC G, OLIVIER C, et al. On the simplifications of cable model in static analysis of large-dimension cable-driven parallel robots[C]// Proceedings of the IEEE/RSJ -the International Conference on Intelligent Robots and Systems. Tokyo: IEEE Conference Publications, 2013: 928-934.

[2] DU J L, CUI C Z, BAO H, et al. Dynamic analysis of cable-driven parallel manipulators using a variable length finite element[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(1): 131-137.

[3] WANG W F, TANG X Q, SHAO Z F, et al. Design and analysis of a wire-driven parallel mechanism for low-gravity environment simulation[J]. Advances in Mechanical Engineering,2015,6(1):810606.

[4] GHASEM A, MARCO C. Direct geometrico-static problem of underconstrained cable-driven parallel robots with n cables[J]. IEEE Transactions on Robotics, 2015, 2(31):468-478.

[5] ZI B, DUAN B Y, DU J L, et al. Dynamic modeling and active control of a cable-suspended parallel robot[J]. Mechatronics, 2008, 18(1):1-12.

[6] PHAM C B, YEO S H, YANG G L, et al. Workspace analysis of fully restrained cable-driven manipulators[J]. Robotics and Autonomous Systems, 2009, 57(9):901-912.

[7] DIAO X, OU M, QI L. Singularity analysis of planar cable-driven parallel robots[C]// Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics. Chengdu: IEEE Conference Publications, 2008:1016-1021.

[8] AMIR M. Stiffness analysis of cable-driven parallel robots[D]. Kingston: Queen’s University, 2013.

[9] SU Y, QIU Y Y, LIU P. Optimal cable tension distribution of the high-speed redundant driven camera robots considering cable sag and inertia effects[J]. Advances in Mechanical Engineering, 2014(4):1-11.

[10] QIAN S, ZI B, ZHANG D. Kinematics and error analysis of cooperative cable parallel manipulators for multiple mobile cranes[J]. International Journal of Mechanics and Materials in Design, 2014, 10(4): 395-409.

[11] BOSSCHER P, IMME E U. A stability measure for underconstrained cable-driven robots[C]// Proceedings of the IEEE International Conference on Robotics and Automation. New Orleans: IEEE Conference Publications, 2004: 4943-4949.

[12] BEHZADIPOUR S. High-speed cable-based robots with translational motion[D]. Waterloo: University of Waterloo, 2005.

[13] BEHZADIPOUR S, KHAJEPOUR A. Stiffness of cable-based parallel manipulators with application to stability analysis[J].Journal of Mechanical Design, 2006, 128(6):1366-1366.

[14] KORAYEM M H, BAMDAD M. Stiffness modeling and stability analysis of cable-suspended manipulators with elastic cable for maximum load determination[J]. Kuwait Journal of Science & Engineering, 2010, 37(1): 181-201.

[15] JIANG Q M, KUMAR V J. Determination and stability analysis of equilibrium configurations of objects suspended from multiple aerial robots[J]. Journal of Mechanisms and Robotics, 2012, 4(2): 437-448.

[16] JIANG Q M, KUMAR V J. The inverse kinematics of cooperative transport with multiple aerial robots[J]. IEEE Transactions on Robotics, 2013, 29(1):136-145.

[17] CARRICATO M, MERLET J P, WATERS T P. Stability analysis of underconstrained cable-driven parallel robots[J]. IEEE Transactions on Robotics, 2013, 29(1):288-296.

[18] LIU P, QIU Y Y, SU Y. On the minimum cable tensions for the cable-based parallel robots[J]. Journal of Applied Mathematics, 2014, 27:1-8.

[19] KAWAMURA S, KINO H, WON C. High-speed manipulation by using parallel wire-driven robots[J].Robotica, 2000, 18(1):13-21.

[20] CARRELLA A, BRENNAN M J, WATERS T P. Cable suspended robots: feedback controllers with positive inputs[C]// Proceedings of the American Control Conference. Anchorage: IEEE Conference Publications, 2002:815-820.

[21] KINO H, YAHIRO T, TAKEMURA F, et al. Robust PD control using adaptive compensation for completely restrained parallel-wire driven robots: translational systems using the minimum number of wires under zero-gravity condition[J]. IEEE Transactions on Robotics, 2007, 23(4):803-812.

[22] OH S R, AGRAWAL S K. A control Lyapunov approach for feedback control of cable-suspended robots[C]// Proceedings of the IEEE International Conference on Robotics and Automation. Roma: IEEE Conference Publications, 2007:4544-4549.

[23] VAFAEI A, AREF M M, TAGHIRAD H D. Integrated controller for an over-constrained cable driven parallel manipulator: KNTU CDRPM[C]// Proceedings of the IEEE International Conference on Robotics and Automation. Alaska: IEEE Conference Publications,2010:650-655.

[24] KHOSRAVI M A, TAGHIRAD H D. Robust PID control of fully-constrained cable driven parallel robots[J]. Mechatronics, 2014, 25(2):87-97.

[25] BABAGHASABHA R, KHOSRAVI M A, TAGHIRAD H D. Adaptive robust control of fully-constrained cable driven parallel robots[J]. Mechatronics, 2015, 25(2): 27-36.

[26] KORAYEM M H, TAGHIRAD H D, BAMDAD M. Dynamic load carrying capacity of flexible cable suspended robot: robust feedback linearization control approach[J]. Journal of International & Robotic Systems, 2010, 60(3): 341-363.

[27] LYAPUNOV A M. The general problem of the stability of motion[J]. Journal of Applied Mechanics, 1992, 11(2):531-534.

[28] ARIMOTO S. Control theory of non-linear mechanical systems[M].Oxford: Clarendon Press, 1996.

[29] LEWIS F L, DAWSON D M, ABDALLAH C T. Robot manipulator control: theory and practice[M]. New York: Marcel Dekker, 2004.

[30] SLOTINE J J E, LI W P. Applied nonlinear control[M].NJ: Prentice Hall, 1991.

[31] Spidercan GmbH[EB/OL].[2016].http://www.spidercam.org.

Motion control strategy and stability of a cable-based camera robot

WEI Huiling， QIU Yuanying， SHENG Ying

(Key Laboratory of Ministry of Education for Electronic Equipment Structure Design, Xidian University, Xi’an 710071, China)

It is very difficult to study and solve the motion stability problem of a cable-based camera robot with one-way cable tension, redundant drive, and high speed maneuvering characteristics. In most of references available, high speed stable motion characteristics and control method of a cable-based camera robot are not adequately considered．For this purpose, a modified PD forward control reguration for its cable length coordinates was presented to ensure its stable motion. Firstly, the dynamic equation for its end-effector was established by using Newton-Euler method. The dynamic model of its drive system was also established. And the dynamic model of the whole system was derived. And then, a tracking control strategy for the camera robot was proposed using a modified PD forward controller for its cable length coordinates based on the whole system’s dynamic model. Further more, the stability of the control strategy was proved with Lyapunov stability theory. Finally, numerical examples showed that the camera robot has a stable tracking performance; the effectiveness of the proposed control strategy is verified.

camera robots; dynamics; control strategy; Lyapunov stability; tracking control

国家自然科学基金资助项目(51175397)

2016-01-05 修改稿收到日期：2016-03-04

韦慧玲 女，博士生，1986年生

仇原鹰 男，博士，教授，1958年出生

TH242

A

10.13465/j.cnki.jvs.2017.09.015