非淹没刚性植物对规则波传播变形影响实验研究
2017-05-13陈杰赵静蒋昌波王瑞雪
陈杰,赵静,蒋昌波,王瑞雪
(1.长沙理工大学水利工程学院,湖南长沙410114;2.湖南省水沙科学与水灾害防治重点实验室,湖南长沙410114)
非淹没刚性植物对规则波传播变形影响实验研究
陈杰1,2,赵静1,蒋昌波1,2,王瑞雪1
(1.长沙理工大学水利工程学院,湖南长沙410114;2.湖南省水沙科学与水灾害防治重点实验室,湖南长沙410114)
在海岸带种植红树林等水生植物可以有效的减小波浪对岸滩的破坏,系统全面地研究植物对波浪传播变形的影响是非常必要的。基于波浪水槽实验,探讨了规则波通过非淹没刚性植物波高的沿程变化,分析了水深、入射波高、植物模型密度及分布方式对反射系数、透射系数与波浪衰减系数的影响,同时与孤立波实验数据进行对比。实验结果表明,随着水深的增加,规则波的透射系数增加、反射系数和波能衰减系数减小;随着入射波高的增加,规则波的透射系数减小,反射系数和波能衰减系数增加。在分布方式相同的情况下,植物模型分布密度增加,规则波的反射系数和波能衰减系数增加,透射系数减小。在规则波入射方向上模型布置越紧密,规则波反射系数和波能衰减系数越大,透射系数越小。分析讨论了植物模型对规则波和孤立波的影响,在入射波要素相同的情况下,孤立波和规则波的能量衰减在50%左右,说明植物模型具有良好的消波作用。
非淹没刚性植物;规则波;波浪水槽实验;传播变形
波浪直接作用于岸滩,会造成岸滩侵蚀后退,相比于传统的护岸措施,红树林不但可以保滩促淤,还可以改善生态环境。我国海南、广东、广西等省份种植大面积红树林,在我国珠江三角洲地区也种植着红树林用来防浪护岸。
近年来,许多学者开展了有关水生植物与波浪相互作用的研究。章家昌(1966)考虑了树木外观的影响,展开大量的物理模型实验,考虑了树木主干和林木枝叶对消浪的影响,提出了相应的植物消波公式。蒋昌波等(2012)、沈超等(2013)、Huang(2011)、王俊(2011)等开展了植物与孤立波相互作用的研究。植物与孤立波的相互作用主要表现为孤立波反射系数和透射系数的变化,影响因素主要有水深、入射波高、植物密度以及分布方式等,研究表明孤立波经过植物后能量有明显的减小,说明植物具有良好的防浪效果。白玉川(2005)、杨建民(2008)、吉红香等(2008)开展了植物与规则波相互作用的研究。影响因素主要有水深、波周期、林带宽度等。植物与规则波的相互作用主要表现为波浪消减系数和波高传递率的变化,研究发现若林带足够宽,波浪消减系数可以达到100%。波浪与刚性植物的相互作用,主要是由于植物与波浪相互作用引起的波浪紊动而达到消减波高降低能量。宋连清(1997)、傅宗甫(1997)、冯卫兵等(2012)开展了柔性植物与波浪相互作用的研究。柔性植物与波浪相互作用还要考虑植物随波浪“振荡”的影响,当植物与波浪达到“共振”时,消浪效果会大大减弱,非淹没植物的消浪效果要好于淹没植物。目前,大多数学者对于红树林的实验研究集中于对红树林的消浪效果的研究。对于规则波在红树林模型中的传播变形研究,以及各因素对规则波传播变形的影响研究较少,对于波浪在非淹没刚性植物中的传播变形也鲜有涉及。
因此,本文基于波浪水槽物理模型实验,研究规则波通过非淹没刚性植物波高的沿程变化,分析水深、入射波高、植物模型密度及分布方式对反射系数、透射系数与波浪衰减系数的影响,同时与孤立波实验数据进行对比分析。
1 理论分析
在二维波浪中,单宽波峰线长度内一个波长范围中所储存的总波能由势能和动能两部分组成,即:

式中:E为总波能,Ek为波浪动能,Ep为波浪势能,ρ为水体密度,g为重力加速度,H为规则波波高,L为规则波波长。
考虑到波浪在传播过程中,波浪与植物模型相互作用而发生反射、透射和衰减,因此总波能E的表达式可变形为:

式中:Er为反射波能、Et为透射波能、Edis为衰减波能。
上式可做如下变换:

由规则波总波能表达式可知,规则波波能与波高的平方成正比,因此上式可变换为:
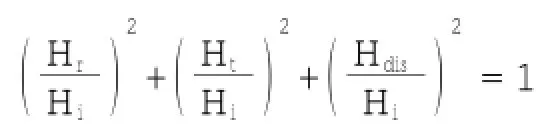
式中:Hi、Hr、Ht、Hdis分别为规则波的入射波高、反射波高、透射波高和衰减波高。
为方便分析,定义Kr、Kt、Kdis分别为规则波的反射系数、透射系数和波能衰减系数,其表达式如下:
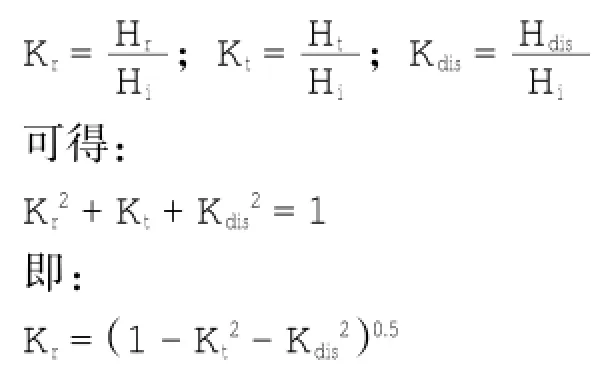
由上式可得,透射系数Kt与波能衰减系数Kdis越大,反射系数Kr越小。通过对规则波反射系数Kr、透射系数Kt与波能衰减系数Kdis的研究,可以了解植物模型对规则波传播变形的影响程度。本实验中影响规则波传播变形的主要因素有水深h,入射波高Hi,植物分布密度φ以及植物分布方式A。以反射系数Kr为例,其表达式可以写为(透射系数Kt和波能衰减系数Kdis可做相同分析):

2 物理模型实验
实验布置如图1所示,实验在长沙理工大学实验中心小波浪水槽内进行。水槽尺寸为40 m× 0.5 m×0.8 m(长×宽×高),水槽两侧为透明玻璃,两端设置消能设施以减少波浪反射的影响。实验所需要的规则波由水槽前端的造波机产生。波高仪(G1~G6)为加拿大WG-50型浪高仪,其数据由江苏东华测试技术有限公司开发的DH5922动态信号测试分析系统采集。

图1 实验布置图(单位:m)
实验模型采用PVC圆管来模拟刚性植物,其优点为刚度接近刚性植物,与波浪作用时不会产生明显变形。实验时将PVC管插置在有机玻璃底板上以便固定模型,底板尺寸为50.0 cm×48.0 cm× 1.6 cm(长×宽×高)。PVC圆管高50 cm,直径为1 cm。根据调查15 a树龄的红树林直径约20 cm左右,树龄20~50 a的红树林直径约15~25 cm,考虑到造波机的造波性能,实验几何比尺采用1∶20。
实际模拟的树干直径为20 cm,满足要求。实验共采用15 cm、20 cm和25 cm共3种水深,根据造波机实际性能,实验采用2.40 cm、5.20 cm、6.30 cm共3种波高。
根据植物的常见种植分布方式,实验共设计6种分布方案,分别为正方形分布、三角形分布、菱形分布和矩形分布。植物分布方案如图2所示,其中,模型M1与M6为正方形分布,模型M3与M4为矩形分布,模型M2为三角形分布,模型M5为菱形分布。

图2 实验模型方案图
为研究植物分布密度对波浪的影响,实验采用下式计算植物分布密度:
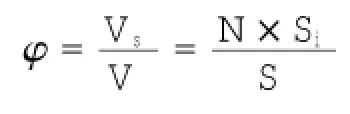
式中:φ为植物分布密度;Vs为植物淹没部分的体积;V为整个分布区域的体积;N为在分布区域内的植物总株数;Si为单株植物横截面面积,实验中为圆管横截面积0.95 cm2;S为整个分布区域面积,实验中为底板面积0.48×0.50=0.24 m2。模型M1-M6分布密度如表1所示,实验组次如表2所示:

表1 实验模型参数

表2 实验组次
实验步骤与蒋昌波等(2012)所做实验步骤相同,实验时,每一次都要等待波面平静后再进行下一次实验,数据采样间隔均为0.02 s。规则波实验波高数据采集时间不少于60 s。
3 实验结果分析
3.1波高变化分析
规则波的传播变形主要表现为波高的沿程变化,为直观体现植物对规则波波高的影响,实验对相对波高H/Hi的变化进行分析,H为各浪高仪测得的实际波高,Hi为实际入射波高。
3.1.1 水深的影响
以G2波高仪所在的位置作为坐标零点,波浪传播方向为正方向建立X轴,各浪高仪所测得的波高值与对应入射波波高的比值为Y轴,分别绘制水深h=15.0cm、h=20.0cm、h=25.0cm,入射波高Hi=2.40cm、周期T=1.0s波况下,模型M1与模型M2的规则波波高沿程变化图,如图3所示。
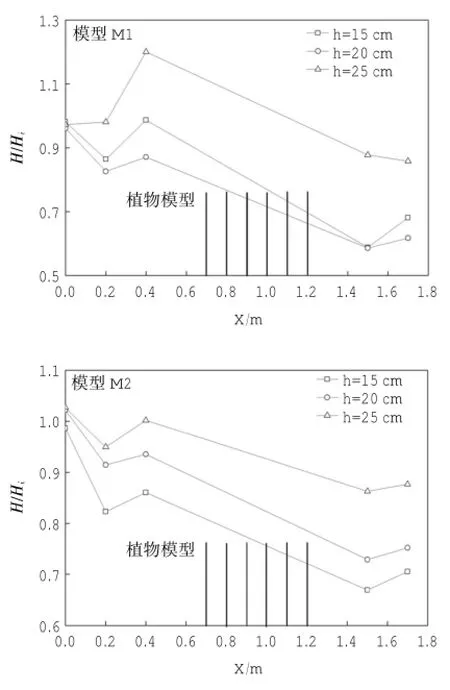
图3 不同水深下规则波波高沿程变化图
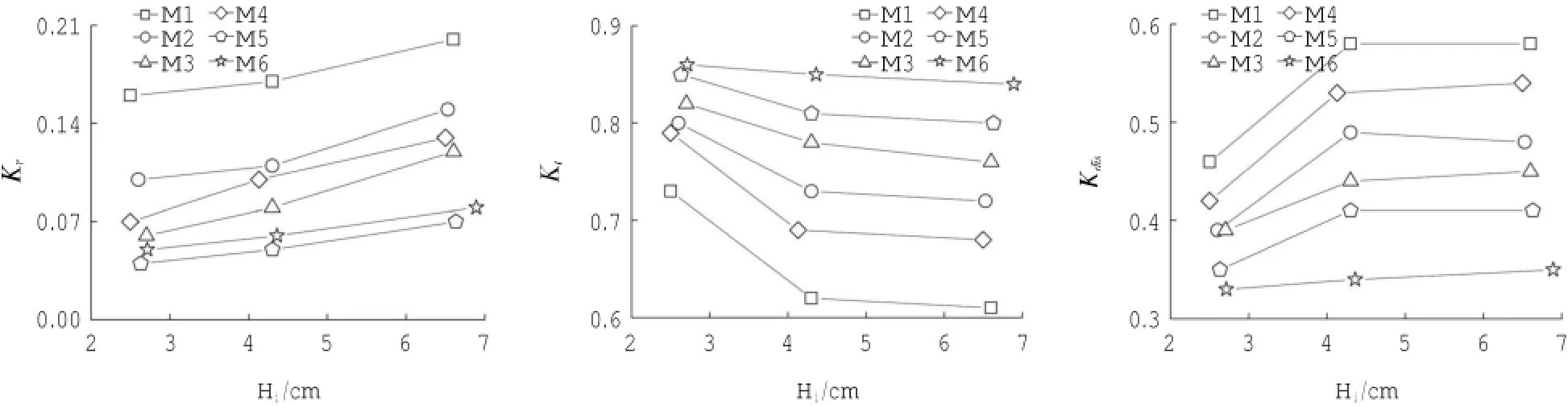
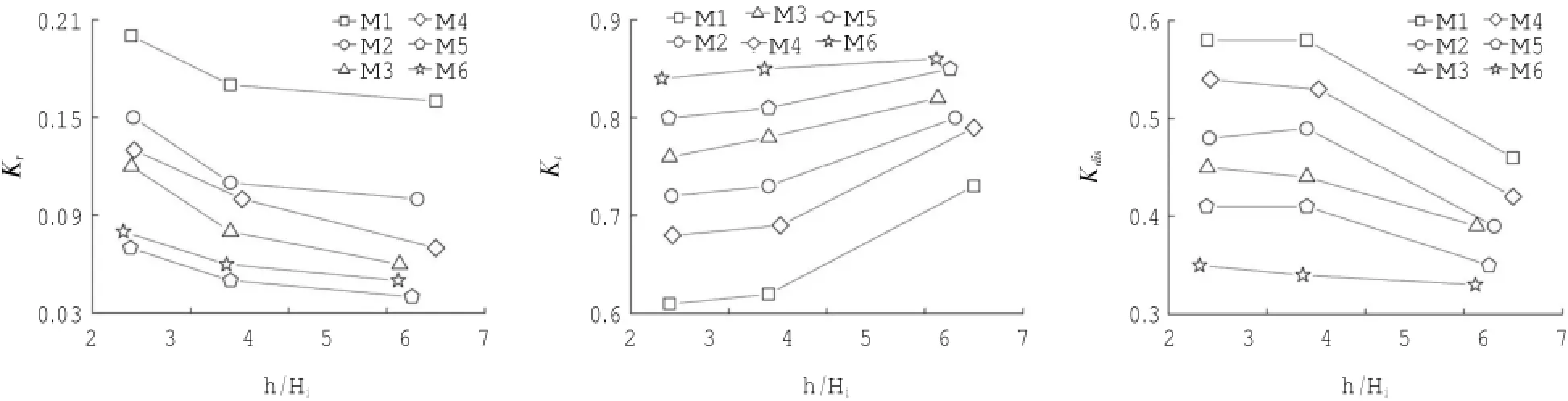
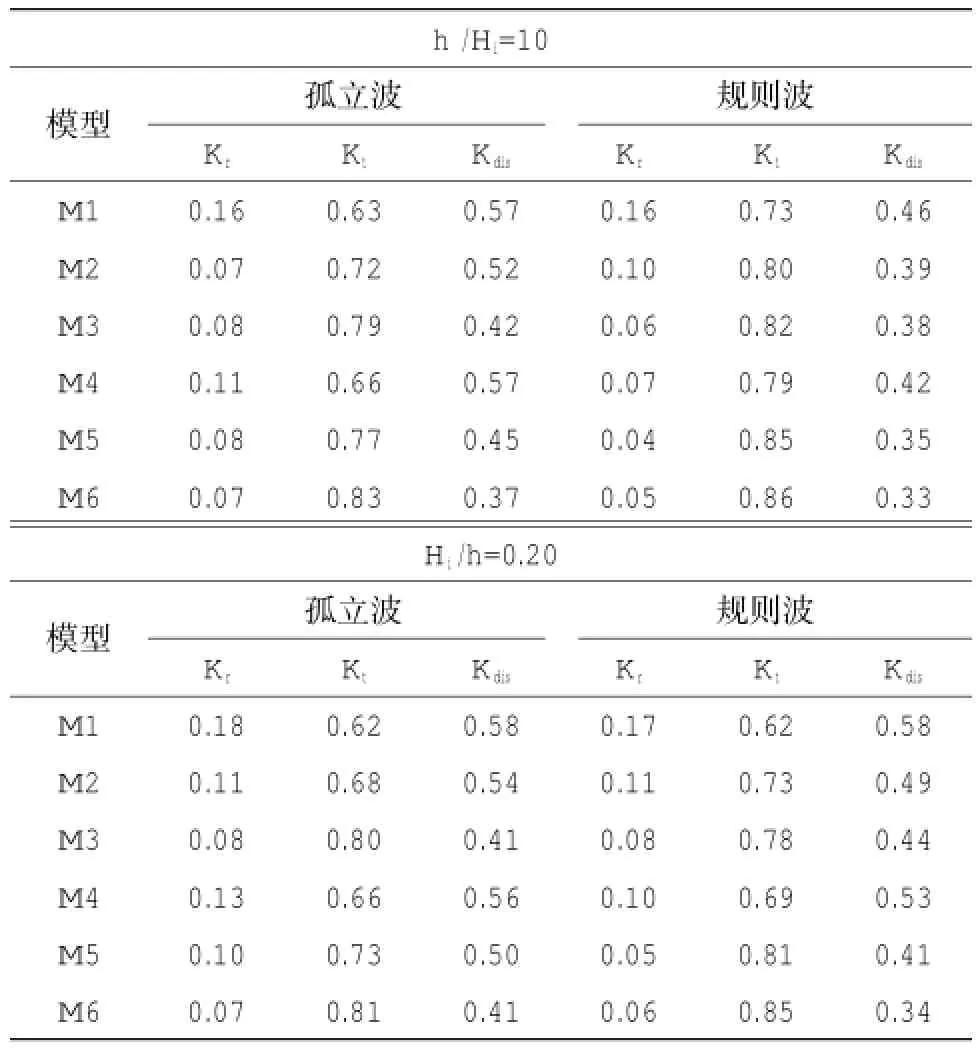
图3 给出了不同水深下规则波波高沿程变化。从图3可以看出,规则波到达植物模型前,波高先变小后变大;经过植物模型,波高保持减小的趋势。波高变小是由于波传播过程中会有衰减和与反射波产生了叠加,经过模型前由于植物模型的阻挡波浪会产生一定的壅高,因而波高变大。经过模型后,由于植物引起的水体紊动造成了波能衰减,使得波高减小。3种水深产生的相对壅高大小:h= 15 cm 3.1.2 入射波高的影响 分别绘制入射波高Hi=2.40 cm、Hi=5.20 cm、Hi=6.30 cm,水深h=25.0 cm波况下,模型M1与模型M2的规则波波高沿程变化图,如图4所示。 图4 不同入射波高下规则波波高沿程变化图 图4 给出了不同入射波高下规则波波高沿程变化。规则波到达植物模型M1与M2前由于植物的阻挡产生了一定的雍高,规则波所产生的相对雍高程度大小为:Hi=2.40cm 3.1.3 植物分布密度的影响 绘制周期T=1.0 s,入射波高Hi=4.40 cm,水深h=20.0 cm与入射波高Hi=5.20 cm,h= 25.0 cm波况下,模型M1~M6的规则波波形沿程变化图,如图5所示。 图5 各植物模型波高沿程变化图 图5给出了不同入射波高下规则波波高沿程变化。规则波到达模型前有不同程度的壅高,经过模型后波高急剧减小,最后趋于稳定。为研究植物分布密度对波高壅高与波高衰减程度的影响,分别绘制植物到达模型前与经过模型后相对波高与植物分布密度关系图,如图6所示。 图6给出了植物到达模型前与经过模型后相对波高与分布密度关系。模型M1-M6的分布密度为M1(0.150)>M3(0.079)>M2(0.075)=M4(0.075)>M5(0.055)>M6(0.040)。上图反应了植物到达模型前波浪壅高程度与植物分布密度的关系。可以看出,规则波的壅高与植物分布密度并不存在明确的线性关系,正方形分布模型M1与M6,分布密度M1(0.150)>M6(0.040),在水深h=20 cm情况下波高壅高程度M1>M6,而在水深h=25 cm情况下M1 图6 波浪到达模型前与经过模型后波高与分布密度关系(上:模型前;下:模型后) 3.2波浪反射系数、透射系数及波能衰减系数的变化 3.2.1 入射波高的影响 图7给出了规则波在6中植物模型作用下的反射系数、透射系数和波能衰减系数随入射波高的变化情况。可以看出,随着入射波高的增加,规则波的反射系数和波能衰减系数增加,透射系数减小。随着入射波高的增加,波浪与植物模型的面积接触增加,规则波水质点的加速度增加,在接触到植物模型时,水质点的速度突变变大,导致水体紊动强度增加,规则波的衰减波能反射波能增加,而透射波能减小。 图7 各植物模型反、透射系数及波能衰减系数随入射波高变化图 图8 各植物模型反、透射系数及波能衰减系数随相对水深变化图 3.2.2 水深的影响 图8给出了规则波在6种植物模型作用下的反射系数、透射系数和波能衰减系数随相对水深(h/ Hi)的变化情况。可以看出,随着水深的增加,规则波的反射系数和波能衰减系数减小,透射系数增大。随着水深的增加,植物模型与水体接触面积增加,淹没体积变大,水体紊动剧烈程度减小,反射波能和衰减波能减小,从而透射波能增大。 3.2.3 植物分布密度的影响 从图8中可以看出在入射波要素相同的情况下,6种植物模型的相对应的反射系数、透射系数和波浪衰减系数。本实验中,模型M1与M6为正方形分布,M2为三角形分布,M3与M4为矩形分布,M5为菱形分布。而分布密度M1(0.150)>M3(0.079)>M2(0.075)=M4(0.075)>M5(0.055)>M6(0.040),从表中可以看出,反射系数、透射系数和波能衰减系数并不随着植物分布密度的变化而单调变化。在入射波要素相同的情况下,波浪的反射系数M1(0.150)>M2(0.075)>M4(0.075)>M3(0.079)>M6(0.040)>M5(0.055),透射系数M6(0.040)>M5(0.055)>M3(0.079)>M2(0.075)>M4(0.075)>M1(0.150),波能衰减系数M1(0.150)>M4(0.075)> M2(0.075)>M3(0.079)>M5(0.055)>M6(0.040),这表明,规则波的反射系数、透射系数和波能衰减系数不仅仅与植物分布密度有关,也与植物分布方式有关。模型M2(三角形分布)、M3(矩形分布)、M4(矩形分布)密度几乎相同,但它们的反射系数、透射系数及波能衰减系数并不相同。模型M1与M6具有相同的正方形分布方式,其反射与波能衰减系数M1(0.150)>M6(0.040),透射系数M1(0.150) 3.2.4 植物分布方式的影响 以模型M2(三角形分布)、M3(矩形分布)、M4(矩形分布)为例,其分布密度基本相同,为M3(0.079)>M2(0.075)=M4(0.075),但分布方式上的不同导致其反射系数、透射系数和波能衰减系数上的差异。 模型M2(三角形分布)与M3(矩形分布)具有相同的株距和行距(a=2l,b=l),反射系数与波能衰减系数M2>M3,透射系数M2 模型M3(a=1,b=2l)与M4(a=2l,b=l)均为矩形分布,其行距和株距有所不同,反射系数与波能衰减系数M4>M3,透射系数M4 为对比分析植物模型对孤立波和规则波的消减影响,利用蒋昌波等(2012)孤立波作用的实验研究成果,开展了对比分析工作。表3给出在相同相对水深(h/Hi=10)和相对波高(Hi/h=0.20)时孤立波和规则波的反射系数、透射系数和波能衰减系数。 表3 相同的相对水深与相对波高情况下孤立波与规则波各系数 波浪经过植物模型后,孤立波和规则波的波能衰减系数在0.3~0.6范围内,说明植物模型具有良好的消浪效果。模型M1与M6均为正方形布置,分布密度M1(0.150)>M6(0.040),孤立波和规则波的反射系数M1>M6,透射系数M1 结合孤立波的研究结果可以看出,不管是孤立波还是规则波,反射系数和波能衰减系数均随入射波高的增大而增大,透射系数均随入射波高的增大而减小。 孤立波和规则波在经过植物模型时,由于植物的阻挡波浪在模型前会产生壅高,相对壅高程度随水深的增加而增加。经过模型时,由于植物引起的水体紊动,波高急剧减小,经过模型后,波高趋于稳定。 随着水深的增加,规则波与孤立波的反射系数和波能衰减系数增大,透射系数减小;随着入射波高的增加,规则波与孤立波的反射系数和波能衰减系数增加,透射系数减小。 无论是规则波还是孤立波,波浪的反射系数、透射系数和波能衰减系数均不随植物分布密度的增加而单调增加,还与植物分布方式有关。分布方式相同时,植物分布密度越大,波浪反射系数和波能衰减系数越大、透射系数越小。分布密度相同时,相比于矩形分布方式,三角形分布方式使得波浪消耗更多的能量,消浪效果更明显。 基于波浪水槽实验,研究了规则波在经过植物模型时的波高的变化,并讨论了入射波高、水深、植物分布密度及分布方式对规则波的反射系数、透射系数及波能衰减系数的影响,结合蒋昌波等(2012)对孤立波的研究,分析了植物模型对孤立波和规则波的影响。研究结果表明: (1)波浪经过模型前,由于模型的阻挡,会产生一定的壅高,经过模型时,由于波浪与模型的相互作用,波高会急剧减小。随着水深的增加,规则波波高的相对壅高程度增加,衰减程度减小。入射波波高越大,波浪相对壅高程度越大,波浪经过模型后,入射波高较小的规则波波高衰减程度小于入射波高较大的规则波。规则波波高的衰减程度基本随植物的分布密度的增加而增加,但分布密度不是唯一的影响因素,分布方式在一定程度上也会影响规则波波高的衰减。 (2)随着入射波高的增加,规则波的反射系数和波能衰减系数增加,透射系数减小。随着水深的增加,规则波的反射系数和波能衰减系数减小,透射系数增加。植物分布密度和分布方式共同影响规则波的反射系数、透射系数和波能衰减系数。在分布密度相同的情况下,植物的株距越小,规则波的反射系数和波能衰减系数越大,透射系数越小。在分布方式相同的情况下,植物分布密度越大,规则波的反射系数和波能衰减系数越大,透射系数越小。相比于矩形分布方式,三角形的分布方式消耗了更多的波能,消浪效果更明显。 Huang,2011.Interaction of solitary waves with emergent,rigid vegetation. Coastal Engineering,38:1080-1088. 白玉川,杨建民,胡嵋,等,2005.植物消浪护岸模型实验研究.海洋工程.23(3):65-69. 冯卫兵,汪涛,邓伟,2012.柔性植物消波特性试验研究.科学技术与工程.12(26):6687-6690. 傅宗甫,1997.互花米草消浪效果试验研究.17(5):45-47. 吉红香,黄本胜,邱秀云,等,2008.滩地植物对波浪变形及消浪效果影响试验研究.广东水利水电,(8):14-18. 蒋昌波,王瑞雪,陈杰,等,2012.非淹没刚性植物对孤立波传播变形影响实验.长沙理工大学学报(自然科学版),9(2):51-56. 沈超,蒋昌波,邓斌,等,2013.刚性非淹没植物对孤立波传播影响的三维数值研究.交通科学与工程,29(1):42-46. 宋连清,1997.互花米草及其对海岸的防护作用.东海海洋,15(1):11-19. 王俊,2011.海岸红树林与海啸波相互作用的实验研究广东水利电力职业技术学院学报.9(3):1-4. 杨建民,2008.海岸带边坡防浪林消浪理论与实验研究.海洋通报,27(2):16-21. 章家昌,1966.防浪林的消波性能.水利学报,(2):49-52. (本文编辑:李晓光) Laboratory investigation on the effects of emergent rigid vegetation on the regular wave transformation CHEN Jie1,2,ZHAO Jing1,JIANG Chang-bo1,2,WANG Rui-xue1 It is known that coastal vegetation conduces to the shoreline protection by damping incoming waves.Effects of water depth,incident wave height,vegetation density,and vegetation arrangement on the reflection,transformation and dissipation coefficients of regular waves are discussed and compared with data of solitary waves.The results show that the transformation coefficient increases as the water depth increases,whereas the reflection and dissipation coefficient decreases. The reflection and dissipation coefficients increase as the incident wave height and vegetation density increase in the same vegetation arrangement,however the transformation coefficient decreases.The more vegetation arranges,the larger reflection and dissipation coefficients are,and the smaller transformation coefficient is.With the same incident parameters,the vegetation is sufficient to dissipate energy of solitary waves and regular waves by about 50%. emergent rigid vegetation;regular wave;wave flume experiment;wave transformation P753 A 1001-6932(2017)02-0222-08 10.11840/j.issn.1001-6392.2017.02.014 2015-06-08; 2016-03-03 国家自然科学基金重点项目(51239001);国家自然科学基金(51409022);湖南省教育厅资助科研项目(13B130);水利部水科学与水工程重点实验室开放研究基金(YK914013)。 陈杰(1982-),男,博士,副教授,主要从事海岸动力过程及其模拟技术研究。电子邮箱:chenjie166@163.com。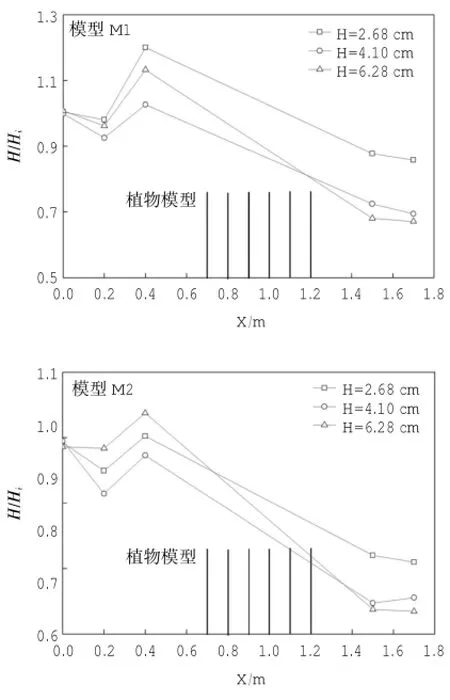


4 讨论
5 结论
(1.School of Hydraulic Engineering,Changsha University of Science and Technology,Changsha 410114,China;2.Hunan Province KeyLaboratoryof Water,Sediment Sciences and Flood Hazard Prevention,Changsha 410114,China)
