大型通风机定子结构减重优化设计研究∗

郭 婷 刘志超 王跃方

（1.沈阳鼓风机集团股份有限公司；2.重大装备协同创新中心沈鼓研究院；3.装备结构分析国家重点实验室）

大型通风机定子结构减重优化设计研究∗

郭 婷1,2刘志超2,3王跃方2,3

（1.沈阳鼓风机集团股份有限公司；2.重大装备协同创新中心沈鼓研究院；3.装备结构分析国家重点实验室）

大型通风机的结构设计应满足强度、刚度、稳定性和动力响应等诸多限制条件。为节省材料、降低成本，提高市场竞争力，风机的质量不能过大。本文提出了带加强筋板的大型风机定子减重优化设计方法。采用结构优化的设计方法，以机壳厚度、筋板高度和筋板厚度为设计变量，考虑应力、位移、稳定性等约束，通过敏感性分析，给出了机壳减重设计的主要途径，以及安全可行的机壳减重设计方案。

通风机；定子；优化；减重

0 引言

通风机的结构设计应满足强度、刚度、稳定性和动力特性等多种要求。目前，大型通风机的设计主要依靠工程经验，工程上一般采取布置加强筋板的方式增强结构刚性。但缺少关于筋板规格、型号和布局的优化设计方法，往往导致风机自重过大、安全裕度过高。为降低成本和提高市场竞争力，需要针对通风机定子的受力特点，研究响应随设计参数的变化规律，使用结构优化设计方法实现安全的减重设计。

定子结构强度分析是通风机减重优化设计的基础。姚鸣和崔国华[1]使用计算和实验方法研究了通风机机壳的振动，发现刚度不足是造成振动过大的原因之一。Bosco[2]用有限元和实验相结合的方法对压缩机壳体进行了受力分析，表明了有限元法在压力容器设计中的应用可行性。钱勇等[3]使用有限元法对离心鼓风机的焊接机壳进行了分析，考察了筋板对机壳强度和密封性的影响，提出了鼓风机机壳的优化设计建议。杨树华[4]等使用ANSYS软件计算了组装式压缩机定子结构在外力作用下的结构应力和变形，根据分析结果对定子结构的设计提出了指导性建议。贺秋冬[5]使用有限元法计算了某轴流通风机机座的应力和位移分布，通过比较分析减少了装置多余的安全裕度。丁如义和田梦远等[6～7]使用ANSYS/Workbench软件中的优化设计模块对轴流压缩机焊接机壳进行了优化。侯秀丽等[8]采用ANSYS/Workbench软件的DOE优化技术确定了某膨胀机蜗壳的优化方案。季学荣等[9]通过研究植物根系成长机理，提出了一种板壳结构加强筋设计方法，对加强筋的分布与截面尺寸进行了优化设计。

结构优化是在现有设计基础上寻找更优方案的过程[10-11]。目前，学术界常用的方法是把设计转化为由设计变量、目标函数和约束函数组成的运筹学模型，运用数学规划算法，通过迭代获取最优设计方案，其执行流程如图1所示。对每个中间方案，分析者都需要重新生成结构模型以确定力学响应，因此，对大型结构来说，传统的数学规划类算法需要动辄上百次的结构及重分析操作，计算耗费巨大，工程上往往难以承受。

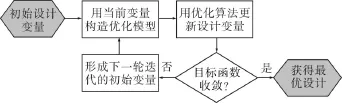
图1 结构优化设计的执行流程图Fig.1 Execution flow chart of structural optimization design

根据通风机结构特点，本文提出了简便、易用的定子结构减重优化设计方法。首先，按照关联程度进行设计变量的分组。考虑目标函数和约束函数的单调性，每组只需计算数种变量组合。对于比较模糊的约束函数，用数值和经验相结合的方法予以考虑。然后，根据灵敏度分析确定设计变量的取值范围，优选出最佳的减重方案。最后，进行强度和稳定性校核，保证设计方案的可靠性。使用此方法，本文对某大型通风机的定子进行了减重优化设计，效果令人满意。

1 定子计算模型与力学分析

通风机定子大多为焊接薄板与加强筋板构成的组合结构。它的承压部件一般由进风筒、出风筒和蜗壳构成（统称为筒体）。为加强筒体刚度，增加结构抗屈曲能力，筒体外表面布置了纵横交错的加强筋板。机壳的材料为Q235钢，密度为7.86t/m3，杨氏模量和泊松比的取值见表1，参考温度为25℃的情况下的热膨胀系数见表2。

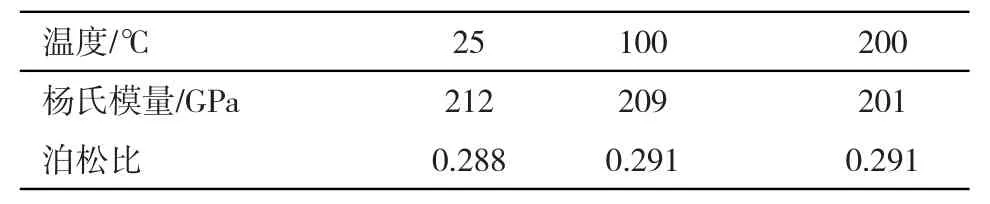
表1 材料属性表Tab.1 Material properties

表2 热膨胀系数表Tab.2 Coefficient of thermal expansion

如图2所示，依据图纸建立了筒体的实体模型。由于壳体厚度远小于其面内尺寸，有限元分析中使用壳单元模拟筒体和筋板，结构分析的有限元模型如图3所示，包括27.8万个节点和9.28万个单元。风机定子受到3种载荷作用：重力、温度和壳体内壁气压。对定子进行有限元分析，依据初始设计方案计算得到了应力和位移结果，分别如图4和图5所示。

图2 风机模型图Fig.2 Fan model

图3 有限元网格图Fig.3 Finite element meshes

图4 风机应力云图Fig.4 Stress distribution of fan

图5 风机位移云图Fig.5 Displacement distribution of fan

2 定子的减重优化设计

2.1 定子优化数学模型

将定子分为出风筒和进风筒两大部分，出风筒包括蜗壳部分。如图6和7所示。进风筒和出风筒都由筋板和筒板组成。筋板高度和厚度以及筒体厚度构成了减重优化的设计变量。按照设计变量的关联程度，把定子分为出风筒筋板、出风筒筒板、进风筒筋板、进风筒筒板四个部分。机壳的优化问题有6个设计变量：出风筒筋板厚度tpo，出风筒筋板高度hpo，出风筒筒板厚度tso，进风筒筋板厚度tpi，进风筒筋板高度hpi，进风筒筒板厚度tsi。其中t表示厚度，h表示高度，下标p表示筋板，下标s表示筒板，下标o表示出风筒，下标i表示进风筒。该优化问题的目标函数为机壳质量M，主要约束为应力响应σ和位移响应d，次要约束为屈曲失稳变形。

优化模型的数学表达式为：

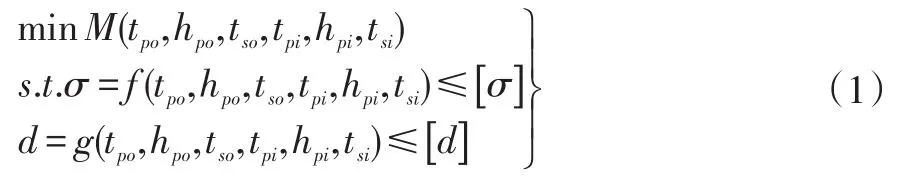
式中，[σ]和[d]分别代表许用应力与位移。

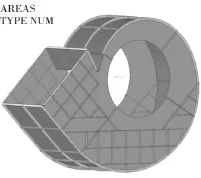
图6 出风筒模型图Fig.6 Outlet tunnel model

图7 进风筒模型图Fig.7 Inlet tunnel model

2.2 敏感性分析与减重方案

定子减重优化的核心是敏感性分析，即约束函数随设计变量变化的敏感程度。改变机壳筋板厚度、筋板高度及筒板厚度尺寸，探明为实现减重目的，各设计变量的取值方向。在做敏感性分析时，以原始尺寸为均值，在此基础上设置增量，形成若干的扰动设计方案，算出应力和位移随设计变量的变化率。表3为出风筒筋板和筒板的设计均值与增量设置，进风筒筋板厚度、高度和筒板厚度的敏感性分析方法与此相同。

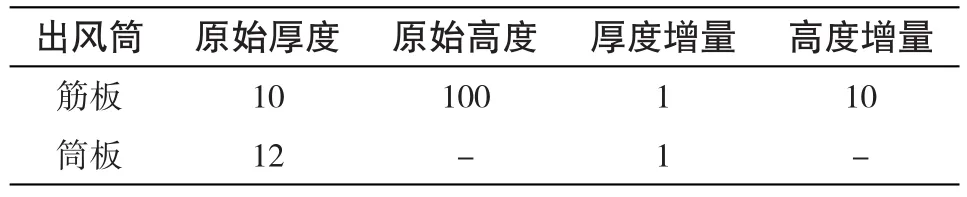
表3 出风筒设计变量的均值与增量Tab.3 Average and increment for the design variables of outlet tunnel mm

按照控制变量法原则，在敏感性分析时，改变筋板尺寸，应保持筒板厚度不变。反之，改变筒板厚度，亦应保持筋板尺寸不变。以此为原则，共形成了62组重分析设计方案，用于计算应力、位移等约束函数对设计变量的敏感性。图8～图11分别显示了出风筒和进风筒的响应约束对设计变量的敏感性分析结果（应力/MPa，位移与尺寸/mm）。

图8 出风筒筋板应力、筒板应力和筋板位移随筋板尺寸的敏感性Fig.8 Sensitivity of the stress in stiffening slab of outlet tunnel,stress intunnel and displacement instiffening slab with respect to the sizes of stiffening slab

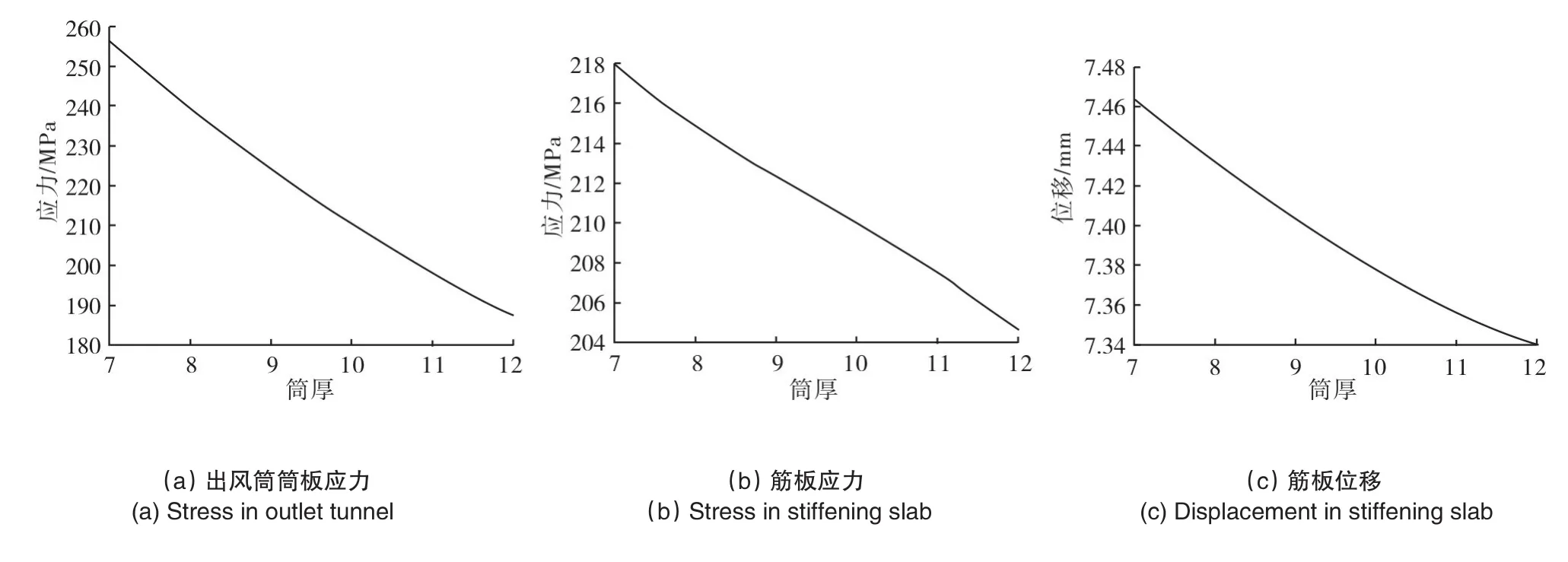
图9 出风筒筒板应力、筋板应力和筋板位移随筒板厚度的敏感性Fig.9 Sensitivity of the stress in outlet tunnel,stress instiffening slab and displacement instiffening slab with respect to the thickness of tunnel

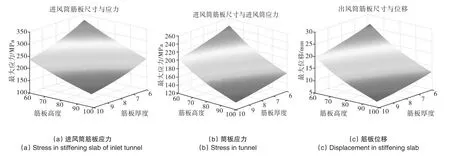
图10 进风筒筋板应力、筒板应力和筋板位移随筋板尺寸的敏感性Fig.10 Sensitivity of the stress in stiffening slab of inlet tunnel,stress in tunnel and displacement instiffening slab with respect to the sizes of stiffening slab

图11 进风筒筒板应力、筋板应力和筋板位移随筒板厚度的敏感性Fig.11 Sensitivity of the stress in inlet tunnel,stress instiffening slab and displacement instiffening slab with respect to the thickness of tunnel

综合敏感性分析结果，可以得出以下结论：

1）大多数筋板及筒板的应力、位移随着筋板尺寸的增加而降低。

2）应力对筋板高度的敏感性较低，对筋板厚度的敏感性较高。位移则正好相反，即位移对筋板高度的敏感性较高，对筋板厚度的敏感性较低。

3）应力和位移对尺寸（高度、厚度）的敏感性随着尺寸的降低而增加，对进风筒筒板而言尤其如此。

4）相对于应力而言，定子的位移对筋板及筒板尺寸的敏感性不大。

根据上述结论，给出下列减重优化对策：

1）若想减轻筋板质量，则优先考虑降低筋板高度。原因是：降低筋板高度比降低厚度更能避免应力的过快上升，而且更能避免结构的屈曲失稳。

2）出风筒的筒板厚度有减重余地。进风筒的筒板虽然也可以减重，但随着尺寸减小，其应力敏感性迅速上升，所以不宜过多地减小厚度。

经过权衡，得到的减重优化方案是：所有筋板厚度不变，高度从100mm减为80mm；蜗壳和出风筒厚度从12mm减为10mm；进风筒厚度从10mm减为9mm。减重前后质量对比如表4所示，定子部分总减重2.6t。

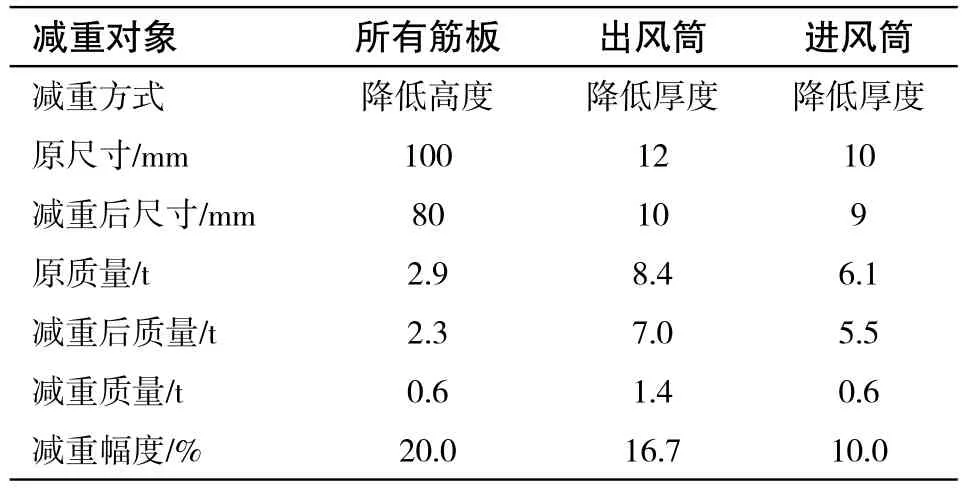
表4 定子减重方案表Tab.4 Weight-reduction scheme for stator

对减重后的结构设计进行校核，结果表明优化后的机壳应力仍远小于屈服应力。从优化设计的角度来说，减重后，应力约束仍为“松约束”，可以保证结构安全性。

2.3 稳定性校核

在进行减重设计时，如果风筒厚度过薄，或者筋板刚度过小，风机结构会因为柔性太大而发生屈曲失稳。通过载荷分析后发现，进风筒内壁存在着负压力，在吸气时存在屈曲失稳的可能性。采用线性失稳理论对结构进行特征值屈曲分析，通过临界载荷倍率对风机进行稳定性校核。

屈曲失稳一般发生在大变形结构上。大变形状态下，结构的平衡方程为[12-13]：

其中，Ke为弹性刚度阵；KG为几何刚度阵；a为位移；p为外力。设外力增大为λp时，几何刚度阵变为λKG。假设系统达到了随遇平衡，也就是线性失稳的临界点，那么在位移有微小扰动Δa时，结构仍能保持平衡，即：

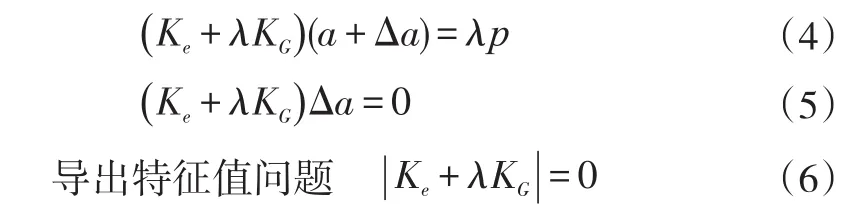
解出λ即可得到发生屈曲失稳时的荷载倍率。需要说明的是，上述推导应用的是线性失稳理论，得到的失稳荷载倍率是理想化的，即在没有“初始偏心”等其他因素干扰下发生的失稳。实际结构中的失稳值往往低于该值，但是使用线性失稳理论得到的荷载倍率在工程中仍具有指导意义。

临界载荷倍率为结构失稳时的内壁压力与设计工况的内壁压力的比值。表5显示了进风筒筋板取不同的高度和厚度时风机的失稳临界载荷倍率。即使是在筋板厚6mm，高100mm的最柔设计下，失稳载荷倍率仍然大于5，不存在筋板失稳问题。可以判定，在目前关心的尺寸变动范围内，可以不考虑结构的屈曲失稳问题。

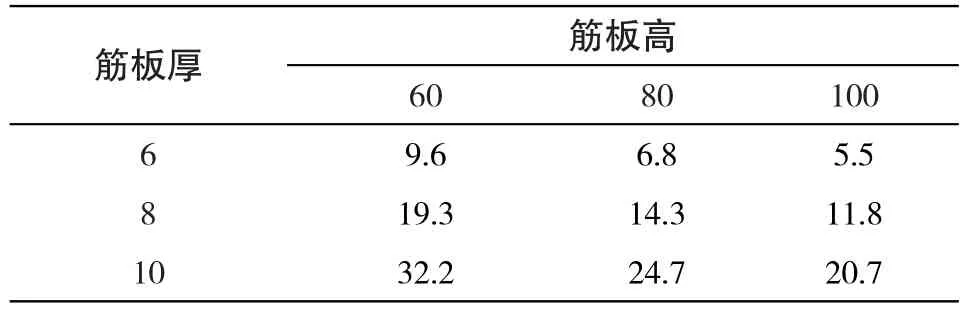
表5 不同筋板尺寸组合下的失稳载荷倍率表Tab.5 Buckling load ratio for different combination with the sizes of stiffing slab

3 结论

根据研究，带加强筋板的大型通风机定子结构的减重优化可分为5步进行：

1）综合考虑制造工艺和安全性等因素，选定优化模型的约束和设计变量;

2）按照关联程度对设计变量分组，减少优化模型的复杂程度;

3）以原有设计为均值，改变设计变量，形成若干扰动设计方案，通过重分析得到各约束关于设计变量的敏感性;

4）根据敏感性分析，找出减轻重量所需的设计变量取值方向;

5）优选出最佳设计变量数值，在减重的同时满足强度、刚度及稳定性。

大型通风机定子的优化设计表明，通过合理地减小风筒厚度、筋板厚度和筋板高度，可得到安全可行的减重设计方案，并为未来风机性能与定子结构的协同设计打下基础。

[1]姚鸣，崔国华.风机机壳振动原因分析与试验研究[J].宇航材料工艺，2000，30(4):17-25．

[2]Bosco R.Numerical and Experimental Stress Analysis of a High Pressure Compressor Using Finite Element Analysis Based on Design by Analysis Criteria[C].ASME 2010 Pressure Vessels and Piping Division/K- PVP Conference.American Society of Mechanical Engineers，2010:897-904.

[3]钱勇，黄文俊.离心鼓风机焊接机壳结构设计与优化[J].风机技术，2014(1):47-50.

[4]杨树华，孟继纲，侯秀丽，等.有限元技术在组装式压缩机定子结构设计中的应用[J].风机技术，2013(4):33-39.

[5]贺秋冬.矿用对旋轴流式主通风机机壳有限元分析[J].煤炭学报，2005，30(3):378-382.

[6]丁如义，孟鑫，田梦远，等.大型轴流压缩机焊接机壳结构设计及优化[J].风机技术，2014(5):39-43.

[7]田梦远，张建勋，丁如义.CAD/CAE在轴流压缩机机壳铸改焊结构设计中的应用[J].风机技术，2012(5)：49-53.

[8]侯秀丽，邱百军，孟继纲，等.膨胀机蜗壳结构改进与优化[J].风机技术，2014(6):56-61.

[9]季学荣，丁晓红.板壳结构加强筋优化设计方法[J].机械强度，2012，34(5):692-698.

[10]钱令希.工程结构优化设计[M].北京：水利水电出版社，1983.

[11]孙焕纯，柴山，王跃方.离散变量结构优化设计[M].大连：大连理工大学出版社，1999.

[12]韩庆华，金辉，艾军，等.工程结构整体屈曲的临界荷载分析[J].天津大学学报，2005，38(12):1051-1057.

[13]任俊超，禹慧，张其林.某国际会展中心的特征值屈曲分析[C].全国现代结构工程学术研讨会，2005.

Design Optimization for Minimum Structural Weight of a Stator for Large Fans

Ting Guo1,2Zhi-chao Liu2,3Yue-fang Wang2,3
（1.Shenyang Blower Works Group Corporation；2.SBW Research Institute of Collaborative Innovation Center of Major Machine Manufacturing in Liaoning；3.State Key Lab of Structural Analysis for Industrial Equipment）

The design of large fans should meet the requirements with respect to strength,stiffness,stability,dynamic response,etc.The weight of large fans should be minimized in order to reduce the material cost.A design optimization method for the weight reduction of a stator with a stiffening slab for large centrifugal fans is proposed in this paper.The design variables are chosen to be the thickness of the casing as well as the thickness and height of the stiffening slabs.The constraints for the stress,displacement and stability are considered.The finite element method is employed for the sensitivity analysis of constraints with respect to the design variables.All details of the weight-reduction design are explained such that the design method can be applied for stators of large fans.

fan，stator，optimization，weight reduction

TH43；TK05

1006-8155（2017）02-0023-06

A

10.16492/j.fjjs.2017.02.0005

辽宁省重大科技创新重大专项项目（201303002）；辽宁省科学技术计划优秀人才培养项目（2014028004）

2017-01-15 辽宁 沈阳 110869