机械通风冷却塔风筒内流场数值模拟研究

2018-07-20解明远赵顺安

中国水利水电科学研究院学报 2018年3期

解明远，赵顺安

（中国水利水电科学研究院，水力学研究所，北京 100038）

1 研究背景

风机是一种利用旋转叶轮将电能转化为空气动能的机械，广泛应用于各行各业。目前，根据统计，风机作为各行业重要的辅机产品，总耗电量占到总发电量的2%左右，在发电行业中，占电厂用电的30%以上[1]。若能提高风机的能量利用效率，则对于节能减排工作有很大意义。在机械通风冷却塔中，风机的作用主要是把经过与水进行热质交换的湿热空气送入大气[2]。风机风筒也是机械通风冷却塔的重要组成部分，其作用主要有两个：一是降低冷却塔风机出口动压，从而减小风机出口动能损失，减少风机能耗；二是可以减小或防止冷却塔排出的湿热空气回流[3]。风筒动能回收性能主要由风机风筒的高度和角度以及线型决定。一般机械通风冷却塔风筒的设计是依据规范来确定的，风筒的高度为1/2D、扩散角10°～ 15°[4]。

对冷却塔风机风筒，国内外学者做了大量的研究：罗金枝等[5]通过对比例为1：10风筒模型进行抽风式模拟实验研究，分析某型号风筒内风速和压力分布，得出风筒筒壁区域动能下降显著，说明风筒角度和高度对冷却塔风机风筒动能回收率具有重要影响作用。对于风机扩散角度，根据流体试验可知，扩散筒的扩散角为14°～18°时流体可不发生分离，所以直线型风筒的线形与垂直线夹角控制在7°～9°[6]。但上述文献中对风机风筒的研究是基于风筒内部气体不存在水平流动进行的，而实际情况是风机风筒内的流动十分复杂，气体除了向风筒出口流动外还存在大量的周向运动。毋飞翔[7]、李红莉等[8]对机械通风冷却塔进行数值模拟计算，得到冷却塔内、外流场分布。但二者都采用fluent内部FAN边界对风机进行模拟，与风机实际运行工况存在差异。周俊杰等[9]对冷却塔风机叶片及其他构筑物进行数值模拟计算，得到了风机及风筒内流场，结果表明风机风筒内流动属于旋转射流，且风机轮毂后有较大回流区域。但文章中没有对空气的旋转射流流动做进一步分析，冷却塔风机风筒的设计应该考虑旋转射流流动的影响。对于风筒高度，许玉林等[10]和周光亮等[11]通过测试得出结论，当风筒高度大于1/2D时，气流与风筒会开始发生分离；对于不同高度风筒进行测量时，发现当扩散角相同，风筒高度为1/2D时风机风量可增大7%，风筒高度为1/3D时，风量仅增大3%。赵顺安等[12]通过试验的方式研究了机械通风冷却塔阻力、风量的特性，对本实验中风机风筒内流场模拟计算可以起到验证的作用。

通过上述研究，风筒能够起到动能回收的作用，且风筒的动能回收率与风筒高度和扩散角有关。但由于旋转射流会使气流扩散角比普通射流更大，且试验和测试结果中很难反映出气体周向运动速度，故使得上述文献的结论不能很好的反应实际情况。本文采用对风机叶片、风筒及整个冷却塔区域进行建模，考虑到风机内旋转射流会使射流扩散角增大，文中将风筒扩散角的研究范围扩大到32°，对比不同的冷却塔风筒扩散角度和高度下风筒的动能回收效率，为风机风筒的设计改造提供参考依据。

2 风筒内流场数值计算

2.1 空气流场控制方程由于冷却塔风速小于1/3音速，所以整个流场内可视为不可压流动，其控制方程包括连续性方程，动量守恒方程和能量守恒方程。并选用RNGk-ε模型[13]对方程进行封闭，各方程如下：

式中：u为速度（m/s）；ρ为空气密度（kg/m3）；p为压力（Pa）；τij为湍流切应力；g为重力加速度（m/s2）；Fi为外源项；k为湍动能；ε为湍动能耗散率（m/s）；Gk为表示由层流速度梯度而产生的湍动能；Gb是表示由浮力产生的湍流动能；YM为可压缩脉动流动对湍流耗散率的贡献；G1ε，G2ε，G3ε是实验常量；δk，δz是k方程和ε方程的湍流普朗特数；Sk，Sz是用户自定义项。

2.2 数值方法和软件简介数值模拟利用商业计算软件Fluent进行，为了计算更快的收敛、使得计算精度得到保证，计算过程中选择有限体积法，利用RNGk-ε湍流模式进行封闭，动量、湍动能、湍流耗散率方程均采用二阶迎风格式进行离散，方程求解时使用SIMPLEC算法。

2.3 模型建立及网格划分以某机械通风冷却塔为研究对象，先采用solidworks对风机扇叶进行建模；后将扇叶导入gambit中对14种风筒和其他构筑物分别进行建模计算，风筒结构如图1所示，风机和扇叶如图2、图3所示。整个塔体建模结果如图4所示。对比分析无风筒情况下与不同规格风筒的动能回收效率和风量变化量。

图1 风筒角度、高度示意

表1 风筒规格

图2 叶片

图3 扇叶

图4 塔体模型

由于风机直径为6 m，分别取风筒高1/3D和1/2D。风筒规格参数如表1。

利用gambit进行网格生成时，综合考虑计算精度和计算能力的要求。对模型区域进行分块划分，对风机扇叶区域、塔筒及其附近区域进行加密。网格如图5所示。

图5 模型网格

2.4 边界条件根据研究对象，将计算域划分为塔内、塔外两个区域：塔外区域，根据风机流场的流动特性，风机扇叶区域和风筒区域流动复杂，计算域选取40 m×30 m×36 m（长×宽×高），塔外区域边界可以看作远场边界，边界设置为压力出口边界。塔内区域，塔体墙壁、轮毂、风机叶片和风筒均设置为无滑移的固壁界面；风筒进出口、填料上下界面等其他界面设置为内部边界；风机旋转区域采用RMF旋转参考系模型，给定转速700 r/s；填料区域采用多孔介质模型。

2.5 数值模拟结果内容由于风筒出口中心位置有比较大的回流区，且风机风速沿径向分布并不均匀，用传统的取断面平均速度求得断面动压，进而得到风机风筒的动能回收率的方法有比较大的局限性。单位时间内通过风机截面的总动能可以由动压的面积分表示，公式为：

式中：E为断面能量（J）；为出口截面法向量；Vi为断面上各点的风速（m/s）；G为风机风量（m3/s）；A为截面面积（m2）。

动能回收率计算公式：

式中：η为风机风筒动能回收率（%）；E1、E2分别为风筒进口和出口动能（J）。

风机风量变化规律统计公式为：

式中：ϕ为风机风量变化率（%）；Qi为加风筒后风机风量（m3/s）；Q1为无风筒时风机风量（m3/s）。

3 计算结果及分析

本文采用三维建模数值计算，对高度为1/3D（2 m）和1/2D（3 m）的风筒在扩散角14°、16°、18°、20°、24°、28°和32°情况下分别进行数值模拟，得到机械通风冷却塔不同风筒下的流场分布情况，对不同风机风筒的动能回收率和风机风量进行对比研究。

3.1 流态分析对比不同高度和扩散角的风筒内流场，发现风筒内流场具有相似性，以风筒高2 m，扩散角16°的风筒为例，得到风筒内流场如图6—图7所示。经过较短的入口风筒，空气进入叶轮旋转区域。从图6中可以看出，受到叶轮的带动，空气有了较大的周向速度，周向最大流速可以达到20 m/s以上，且流体有从叶轮中心向筒壁处流动的趋势，空气速度从叶片中心轮毂处向风筒壁方向速度逐渐变大。通过图7迹线图可以看出，风机风筒内的流体运动属于旋转射流，流体在叶轮旋转区时有较大的周向速度，随着流体向风筒出口处流动，流体的周向速度减小，主要以垂直风筒截面方向流动为主。

图6 风机叶片上断面速度矢量图

图7 迹线图

风筒高度和扩散角不同，风筒内空气流态也会发生改变。风筒内的速度矢量图和压力云图如图8和图9所示。从图8（a）和图9（a）可以看出，由于风机轮毂后方流体流动速度小，且扇叶区域内流体有向远离风筒中心方向流动的趋势，所以流体在风机风筒的中心区域形成比较大的低压回流区，回流速度较小，导致风筒出口断面的风速分布很不均匀，远离风筒中心处流体流速较大，中心区域流速较小。

从图8（b）和图9（b）以及各型号风筒的动压分布图中可以看出，风机风筒扇叶远端处动压最高，风筒边壁处会有低压区。且随着风筒角度的增大和风筒高度的增加，风筒边壁处低压区逐渐开始扩大，即流体主流开始逐渐与风筒边壁分离。从图9（b）中可以看出，风筒高3 m，扩散角为28°时，风筒边壁处已经出现明显流动分离。

3.2 风筒尺寸对动能回收率的影响通过分析风机出口平均动压可以得到，当不设置风筒时，风机上断面动压为70.03 Pa，设置风筒后由于风筒出口面积较大，出口速度减小，风筒出口动压基本小于50 Pa，所以设置风筒对于风机减少动能损失是十分必要的。

图8 风筒高2m，扩散角16°时，风筒内速度压力分布

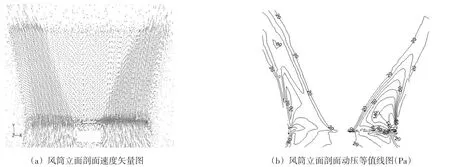
图9 风筒高3m，扩散角28°时，风筒内速度矢量和压力（Pa）分布

通过公式（2）（3）分析各种型号尺寸的风筒的动能回收率，如图10所示。可以看出风机风筒的动能回收率都在30%～40%左右。但可以看出风机风筒在风筒扩张角度相同时，风筒高度为3 m时比风筒高2 m时的动能回收率大。并且当风筒扩散角由14°增大到32°时，两种高度风筒的动能回收率的变化规律都是先增大后减小：风筒高3 m时，当扩散角为18°时动能回收率达到最大值，为38.90%；风筒高2 m时，扩散角为20°时动能回收率达到最大值，为36.17%。这是由于风筒高3 m时比风筒高2 m时，流体在流动中先发生分离。

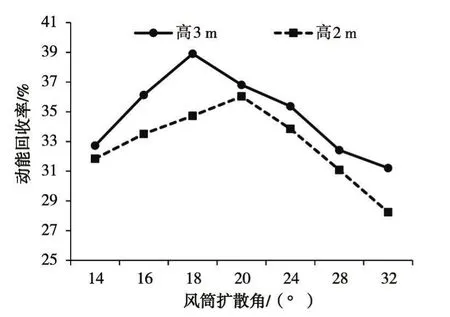
图10 动能回收率变化规律

图11 风机风量变化规律

3.3 风筒尺寸对于风量的影响冷却塔风机风量变化通过统计公式（4）得到，如图11所示。安装风筒后风机风量比无风筒时大，风筒扩散角在14°～20°之间时，3 m高风筒的风量大于2 m高风筒的风量。风筒高3 m时，当扩散角为18°时，风机风量达到最大值，较无风筒时增大8%；风筒高2 m时，风筒扩散角20度时，风机风量较无风筒时约增大4.5%。当风机风筒扩散角大于20度时，风机风量开始下降。