例谈“参数范围”问题的解题策略

☉浙江省诸暨市海亮高级中学 沈铁表

例谈“参数范围”问题的解题策略

☉浙江省诸暨市海亮高级中学 沈铁表

近几年的高考中，求参数的取值范围是高考数学试题中经常考查的典型问题，作为一个常考的热点，也是高中数学中的一个重要内容.下面谈谈这类题型的典型解决方法.

一、利用分离参数求参数范围

分离参数是高中数学解题中常见的解题方法，因为避开了分类讨论，具有思路清晰，易于操作等特点，深受师生的青睐.

（1）若f（x）在x=0处取得极值，确定a的值，并求此时曲线y=f（x）在点（1，f（1））处的切线方程；

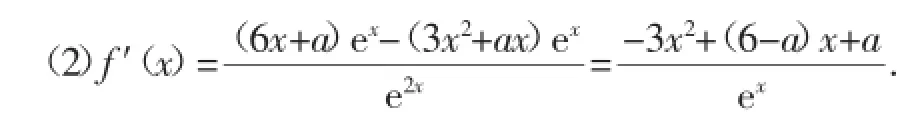
因为ex＞0，由-3x2+（6-a）x+a≤0，得a（1-x）≤3x2-6x.

点评：本题解法众多，而通过分离参数，将参数a可直接分离出来，从而使得问题变得非常简单.

二、利用构造函数求参数范围

题目中如果涉及不等式、方程等问题，常常建立目标函数，并确定函数的定义域，用函数的方法分析，此类问题的解决方法即为构造函数.构造函数在解决参数问题时常常起着重要的作用.

例2已知函数f（x）=ex-ax，其中a＞0.

（1）若对一切x∈R，f（x）≥1恒成立，求a的取值集合；

（2）在函数f（x）的图像上取定两点A（x1，f（x1）），B（x2，f（x2））（x1＜x2），记直线AB的斜率为k，证明：存在x0∈（x1，x2），使f′（x0）=k成立.

解：（1）f′（x）=ex-a.令f′（x）=0，得x=lna.

当x＜lna时，f′（x）＜0，f（x）单调递减；当x＞lna时，f′（x）＞0，f（x）单调递增.

故当x=lna时，f（x）取最小值f（lna）=a-alna.

于是对一切x∈R，f（x）≥1恒成立，当且仅当aalna≥1.①

令g（t）=t-tlnt，则g′（t）=-lnt.

当0＜t＜1时，g′（t）＞0，g（t）单调递增；

当t＞1时，g′（t）＜0，g（t）单调递减.

故当t=1时，g（t）取最大值g（1）=1.因此，当且仅当a= 1时，①式成立.

综上所述，a的取值集合为｛1｝.

（2）证明略.

点评：先构造新函数g（t）=t-tlnt，再利用导数方法求得最值即可.

三、利用不等式放缩求参数范围

已知一个不等式求其中参数的范围，直接证明比较困难，常常利用合理的放缩达到所要证明的结果.

（1）判断函数h（x）是否为补函数，并证明你的结论；

（3）当λ=0，x∈（0，1）时，函数y=h（x）的图像总在直线y=1-x的上方，求p的取值范围.

解：（1）函数h（x）是补函数，证明略.

所以点（xp，h（xp））不在直线y=1-x的上方，不符合条件.

设φ（x）=xp+（1-x）p，x∈（0，1），

则φ（′x）=p［xp-1-（1-x）p-1］.

又因为φ（0）=φ（1）=1，所以当x∈（0，1）时，φ（x）＜1恒成立.

综上所述，p的取值范围是（1，+∞）.

点评：本题考查导数的应用、函数的新定义，函数与不等式的综合应用以及分类讨论，数形结合的数学思想.

四、利用判别式求参数范围

实系数一元二次方程ax2+bx+c=0有无实根的依据——判别式为Δ=b2-4ac≥0是否成立，因此常常将问题转化为一元二次方程是否有根，通过判别式得到参数范围.

例4设a＜1，集合A=｛x∈R|x＞0｝，B=｛x∈R|2x2-3（1+ a）x+6a＞0｝，D=A∩B.

（1）求集合D（用区间表示）；

（2）设函数f（x）=2x3-3（1+a）x2+6ax在D内有极大值点，求a的取值范围.

解：（1）x∈D⇔x＞0且2x2-3（1+a）x+6a＞0.

令h（x）=2x2-3（1+a）x+6a，则

Δ=9（1+a）2-48a=3（3a-1）（a-3）.

所以B=（-∞，1）∪（1，+∞）.

于是D=A∩B=（0，1）∪（1，+∞）.

因为x1＜x2且x2＞0，所以B=（-∞，x1）∪（x2，+∞）.

又x1＞0⇔a＞0，所以

②当a≤0时，D=（x2，+∞）.

（2）f（′x）=6x2-6（1+a）x+6a=6（x-1）（x-a）.

当a＜1时，（fx）的单调性如下表：

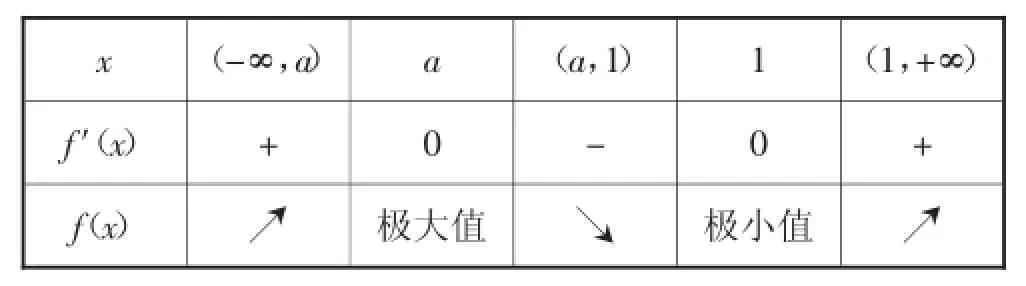
由表可么，x=a为（fx）在D内的极大值点，x=1为（fx）在D内的极小值点.

由表可得，x=a为f（x）在D内的极大值点.

④当a≤0时，D=（x2，+∞）且x2＞1.

由表可得，f（x）在D内单调递增.

因此f（x）在D内没有极值点.

综上所述，a的取值范围是（0，1）.

点评：解决时借助了一元二次方程的判别式，并结合导数与极值之间的关系.

总之，对于平时常考常新的题型，若能细致分析、挖掘，不但能提高教师的教研水平，提高教学效益，而且还有助于提高学生的解题能力，增强解题信心.引导学生在解题中不断总结经验，学生全面细致地分析问题，总会收到事半功倍的效果.