让探究成为高三微专题复习课的主旋律*
——以一节高三微专题复习课为例
2017-05-12广州市真光中学吴润文
☉广州市真光中学 金 明 吴润文
让探究成为高三微专题复习课的主旋律*
——以一节高三微专题复习课为例
☉广州市真光中学 金 明 吴润文
一、问题提出
在高三复习课的教学中,为了突出重点,突破难点,提升能力,常常在重点内容开设微专题复习课.微专题复习课涉及的教学内容一般不多,它围绕若干紧密相关的知识或确定的思想方法形成一个教学小专题,以具有一定综合性的教学内容为载体,以形成知识网络,产生对知识整体认识为指向,以提升学生综合运用某些知识解决数学问题、提升能力为目的.由于微专题复习课具有操作灵活、指向性强,对提高学生能力有很好的实效性等特点,所以在高三教学中经常被采用.
但在微专题教学实践中,很多微专题课显现出“目标定位过大,过于追求综合,过于追求容量与节奏,忽视动态生成,问题设计不够合理,就题论题,思维含量过少”等问题,导致教学效果不好,简单重复,没有新意,学生兴趣不高,学习积极性和主动性难以发挥.
如何使微专题复习课有效高效呢?笔者认为应该让专题“微”起来,表现在选材上适合学生实际与考纲要求,突破学生学习难点,“微”在难点突破;表现在教学过程上,“微”在精心预设,让学生的学习活动成为探究的过程;表现在操作上,“微”在互动生成,让自探、互探、悟探融为一体.下面以微专题《抛物线的切线问题》为例加以分析说明.
二、微专题《抛物线的切线问题》课堂教学实践
教学前的思考:为什么将《抛物线的切线问题》选材为一个微专题进行教学?原因是《抛物线的切线问题》关注了知识的交汇(抛物线的有关知识与导数的相关知识),它的切入点可以从直线与抛物线的位置关系(相切,用根的判别式解决),也可以用导数的几何意义解决切线问题,到底如何选择较好?对学生来说是一个难点.同时此内容适合学生的需求,学生对抛物线与导数知识有一定的了解,但对它们的联结点、交汇点认识不深刻,需要进一步探讨.同时本内容是高考命题的热点,通过本内容的学习,可提高学生分析问题、解决问题的能力.
1.特例引入,降低起点,激发学生探究兴趣
引例:已知抛物线x2=4y,抛物线的准线与y轴交点为P,若过P作抛物线的切线,切点分别为A,B.
(1)求切线PA,PB的方程;
(2)求直线AB的方程.
(学生自主探究6分钟后投影展示学生的解答过程)
生1:依题意得,抛物线准线为y=-1,故P点的坐标为(0,-1).
设PA的方程为y+1=kx,因它与抛物线x2=4y相切,
即方程x2=4(kx-1)有两个相等实根.
所以Δ=(4k)2-16=0,即k=±1.
所以PA,PB的方程为y=x-1,y=-x-1.
易知A,B坐标为(2,1),(-2,1),故直线AB方程为y=1.
所以直线PA,PB的方程为y=x-1,y=-x-1.
同理可得直线AB的方程为y=1.
师:生1、生2的解法非常好,他们从不同的角度解决了有关抛物线的切线问题.哪位同学能总结一下他们的方法?
生3:生1是应用直线与抛物线相切,方程组只有一组解转化为方程有两个相等的实数根来求解的.生2是用导数知识设切点,根据切线斜率是函数在切点处的导数而得到切线方程.
师:生3总结得非常好!他总结了解决抛物线切线问题的两种方法.请同学们思考一下,点P在特殊的位置(如准线上),此时切线PA,PB有何关系?直线AB过一个特殊的点吗?点P在准线其他位置有这种关系吗?
教学感悟:教学从一个简单的、特殊的实例出发,让学生自主探究;通过展示学生的解法,让学生体验成功,以激起学生进一步探究的欲望.让学生总结归纳,建立解决问题常用方法的理论依据以及不同解题方法之间的联系与区别,帮助学生形成知识网络.教师提出新的数学问题,引导学生进一步探究.
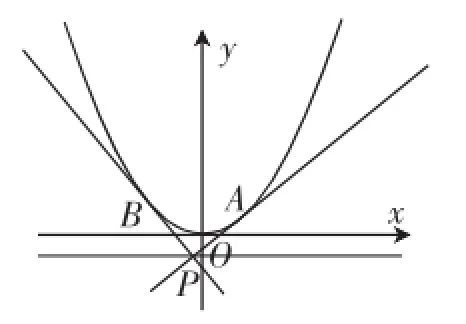
图1
2.问题驱动学生自主探究合作交流
探究1:过抛物线x2=4y的准线上任意一点P作抛物线的切线PA,PB,则PA,PB有什么关系?直线AB过定点吗?
生4:(教师展示生4的解法)设直线PA的方程y+1= k(x-x0).因为它与抛物线x2= 4y相切,所以x2=4(kx-kx0-1),即x2-4kx+4kx0+4=0.(1)
此时由判别式Δ=16k2-4·(4kx0+4)=0,得k2-kx0-1=0.(2)
……做不下去了.
师:生4做到这里就做不下去了,哪位同学能帮助他?
生5:由(2)知,k1k2=-1,故PA,PB垂直.
师:为什么?
生5:因为PA,PB是过点P的抛物线x2=4y的两条切线,
所以方程k2-kx0-1=0的两根分别为PA,PB的斜率.
由韦达定理知,k1k2=-1.故PA,PB垂直.
师:生5讲得非常好,理解得很透彻.直线AB过定点吗?如何求解呢?
生5:好像不好做,若通过(1)式解方程求A,B两点的坐标应当可行,但运算量太大,不可行.不知怎么办?
师:有哪位同学想到解决问题的方法吗?
故直线AB过抛物线x2=4y的焦点F.
师:生6的推导非常正确,它说明过抛物线准线上一点作抛物线的两条切线,则这两条切线互相垂直,且两切点的连线过焦点.反之其逆命题是否成立呢?
教学感悟:教师创设了一个开放性问题情境,激发学生探究.因问题的开放性,学生思考的视角增大,且难度不太大,入手点多,有助于学生主动参与探究,激发学生学习的积极性.教学中,教师充分留给学生思考、尝试、探究的时间与空间,使学生能从各自的角度认识问题,鼓励学生从不同角度思考问题,提出不同的解决方案.当学生有问题时,鼓励学生相互讨论,合作交流.在合作与交流中,学生得到了问题的正确解法,澄清了错误的认识,体会到了不同解法的区别与联系,悟出了简洁的解法合理性.在学生理解困难的关键处提出质疑,让学生思考,深化学生思维.同时,提出了新的问题(原问题的逆命题)引发学生思考.
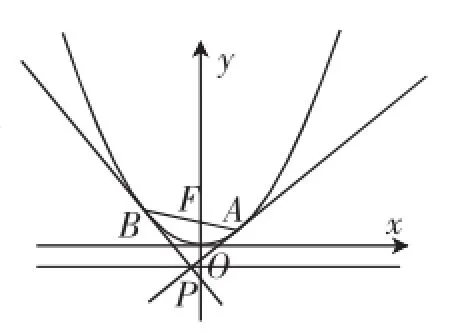
图2
探究2:如图2,过抛物线x2=2py的焦点F任作一条直线交抛物线于点A,B,过点A,B作抛物线的切线l1和l2,两条切线交于点P,则点P的位置在什么地方?

所以点P在准线上.
师:生7解答得非常好,通过她的解答,可得出如下结论:过抛物线焦点作直线交抛物线于A,B两点,过这两点分别作抛物线的切线,则两切线交于抛物线的准线上.现有一个问题值得同学们探究一下:若不是过焦点,结果如何呢?
教学感悟:探究2是对探究1的逆命题的探究,学生因有探究1的解题经验,解答此题就有了相似的方法,学生的探究的兴趣也愈来愈浓.同时,探究2的设计给学生的自主探究指明了方向:对于一个数学问题可从哪些方面进行探究?如可探究问题解法的多样性,也可变换命题,如将条件变结论,结论变条件命题是否成立,还可变换条件;扩充结论等,为学生的自探自悟奠定了基础.教师通过总结,又提出了新的探究问题,同时为学生的自探指明方向.

图3
探究3:如图3,已知抛物线x2=2py(其中p>0),若点P(x0,y0)为坐标平面内的一定点,过点P的动直线l与抛物线交于点A,B,过点A,B作抛物线的切线l1和l2,两条切线交于点Q,则点Q的轨迹方程是什么呢?

得x2-2pkx+2pkx0-2py0=0.
则x1+x2=2pk,x1x2=2pkx0-2py0.下面就不知如何做了?
师:哪位同学能帮帮忙?
生9:生8已经接近成功了,只需设点Q的坐标为(x,y),
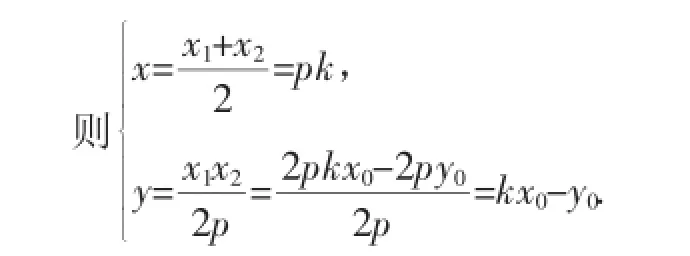
消去k,得x0x=p(y+y0).
故点Q的轨迹方程为x0x=p(y+y0).
师:非常好.经过生9的补充,此题得到完美的解答.此题求Q点的轨迹,实质是用到了参数法求轨迹,通过消去参数k得到轨迹方程.生8之所以没有成功,是对参数法求轨迹理解不到位,希望大家继续努力.
师:(因接近下课,课堂小结)请同学们思考一下,我们今天学习了什么?解决了什么问题?方法是什么?
生10:今天,我们学习了抛物线的切线问题,解决了形如x2=2py的抛物线的切线问题.
生11:解决抛物线的切线问题的方法有两个,其一是应用直线与抛物线相切,方程组只有一组解转化为方程有两个相等的实数根来求解的.其二是用导数知识设切点,根据切线斜率是函数在切点处的导数而得到切线方程.
师:非常好,还有什么值得我们探究的问题吗?
生12:形如y2=2px的抛物线的切线问题.
生13:圆的切线问题?椭圆的切线问题.
师:提出问题是成功的一半,非常好,同学们提出这些问题作为我们今天的作业.
教学感悟:探究3是将探究2从特殊到一般的探究,它沟通了直线与抛物线,抛物线的切线方程,交点的轨迹问题等知识的联系.通过此题的探究,可提升学生综合分析问题的能力.同时指明了自探、悟探的方向.教师的小结也别具一格,不仅让学生总结提炼所学知识,而且让学生思考值得探究的问题,将探究延伸.
3.延伸探究,自探自悟
设计一些探究性问题,留作课后思考,让学生自探自悟.
探究4:过抛物线y2=2px的准线上任意一点作抛物线的切线PA,PB,则PA,PB的位置有什么关系?直线AB过定点吗?
探究5:过点P(m,0)的直线与抛物线y2=2px交于点A,B,分别过A,B作抛物线的切线l1和l2,且l1和l2的斜率分别为k1和k2,则k·1k2是否为定值?
探究6:已知抛物线y2=2px(其中>0),若点P(x0,y)0为坐标平面内的一定点,过点P的动直线l与抛物线交于点A,B,过点A,B作抛物线的切线l1和l2,两条切线交于点Q,求证:点Q的轨迹方程为y0y=p(x+x0).
探究7:已知圆O:x2+y2=r2,若点P(x0,y0)为坐标平面内的一定点(异于圆心O),过点P的动直线l与圆O交于点A,B,过点A,B作圆O的切线l1和l2,两条切线交于点Q,求证:点Q的轨迹方程为x0x+y0y=r(2除圆内部分).
设计说明:探究4-6是另一种形式的抛物线切线问题的有关探究,它的处理方法如何?与课堂上的抛物线切线问题解决方法是否相同,值得让学生课后探讨.探究7-8是圆与椭圆的切线问题的探究.通过对各种曲线的切线问题的探究,可沟通知识联系,激发学生学习兴趣,培养学生勇于探究,乐于探究的好习惯.
三、教学思考
微专题复习课是基于学情、教情,选择切口小、角度新、针对性强的微型复习专题,力求解决复习课中的真问题、小问题和实问题.选择怎样的主题,以怎样的教学方法解决问题是微专题教学效益的关键,结合本课,笔者认为搞好微专题复习课要从以下几个方面入手:
1.精选教学内容,定点突破
微专题内容的选择目的是解决学生学习中的“困惑点”“疑难点”,内容选择应在学生的“思维最近发展区”内进行,不宜过易也不宜过难.知识和方法不能一蹴而就,要把握好度,所选内容既要让学生在课堂上巩固基础知识,熟练掌握基本解题方法,又要激发学生学习积极性,使学生主动参与、乐于探究、勤于动手,所以内容要精、要具有研究性,可以从多个角度认识和解决问题,具有一定的思维含量,能够体现核心的思想方法.如本节课的内容选材关注解析几何与导数的联结点,高三学生可从多个角度展开研究,研究的角度多样、解题方法多样,本节课精心设计了一系列问题,由浅入深,由简单到复杂,由特殊到一般.通过学生的探究,可沟通知识的联系,体验到不会的痛苦与成功的喜悦,有助于进一步激发学生的学习兴趣.
2.学生主体,探究成为课堂教学的主旋律
微专题教学的课堂,因教学内容是学生的易混易错点,是综合知识的联结点,教师的教学要关注学生为什么会易混易错,为什么感觉困难.因此,教学理念一定要以学生为主体,根据学情以学定教,设计问题由浅入深,符合学生最近发展区,让学生独立思考、主动探究,让学生展求思维过程、互相合作、补充,教师引导.本节课在探究问题1时,让学生展示多种解法,剖析做不下去的原因;引导学生换个角度思考问题;再让别的学生补充、交流.把课堂真正还给学生,让学生探究、交流、再探究、再交流;让学生在参与教学活动中激活思维、经历过程.除了课堂内探究外,再设计问题拓展延伸,让学生在课外也有探究的问题与时空.
3.教师主导,精心设计问题;教学组织,突出生成性
微专题教学内容是教师根据学情精心设计的.通过微专题教学,教师可以引导学生“综合考点,把握重点,关注热点,查找漏点”,将学到的知识、技能、方法形成一个有机的整体,把握知识间的联系,归纳总结解题方法,整合知识要点,渗透数学思想,提升数学能力.课堂教学是预设与生成的有机组合,预设是为了更好的生成.微专题教学目标的达成不是教师用简单的方式直接灌输给学生,而是让学生在课堂上经历解决问题的过程,通过生生、师生的互动而生成.如本节课的教学,教师精心预设了问题,得到答案的过程不是教师直接灌输,而是由学生合作交流完成.老师只是引导学生从哪些方面探究,渗透自探、悟探的问题与方法.
1.徐勇.在错误中寻找学生的最近发展区[J],中学数学教学参考(上旬),2010,7.
2.李建潮,宋卫成.摭探数列前n项和的适当放缩[J],中学数学教学参考(上旬),2010,10.
3.金明,贺育林.要短效高分,还是长效能力[J].数学通讯,2015,5.
4.金明,叶东芳.研一题悟一法通一类[J].中学教研,2015,10.
(1)2016广州市教育规划课题《数学课堂探究式教学的实践研究》课题编号1201574155.(2)广东省“十二五”规划课题《提升高中数学教师教学能力的研究》课题编号2013YQJK080
