由一道高考题探究二面角的解法

☉安徽省阜阳市临泉第一中学 熊文文

由一道高考题探究二面角的解法

☉安徽省阜阳市临泉第一中学 熊文文

立体几何试题是高考的常客，其中二面角问题是立体几何的考查中的重点，它既可考查逻辑推理能力，又可考查运算求解能力.对学生知识以及思维能力要求较高，学生在求二面角时，往往无从下手，正确率较低.本文就一道全国卷立体几何问题，从代数方法和几何推理两方面探究二面角的解法，仅供大家参考.

一、二面角常见解法回顾

（1）几何法.通过几何推理，找到二面角的平面角，再用解三角形的知识，求出平面角的大小.如图1，通常先确定二面角的棱，再在棱上确定一点，找棱的垂面，从而找到平面角.

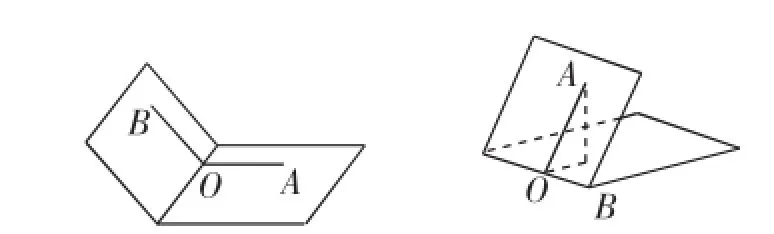
图1

（2）代数法.如图2，通过建立空间直角坐标系，利用平面的法向量，求二面角的余弦值.

图2

（3）代数几何法.如图3，通过几何法，找到棱的垂线，再由代数法，求出两条垂线（或者向量）所成的角.

图3

二、解法展示

例题（2013年全国卷理19）如图4，四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB和△PAD都是等边三角形.

图4

（1）证明：PB⊥CD；（证明不再给出）

（2）求二面角A-PD-C的余弦值.

解法1：取BC中点E，连接AE，交BD于点O，连接OP.由（1）知，OE，OB，OP两两垂直.

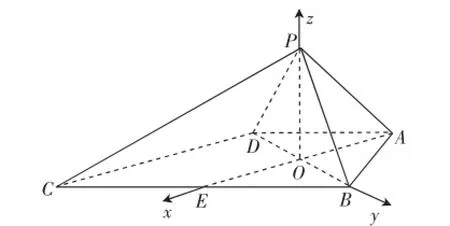
图5

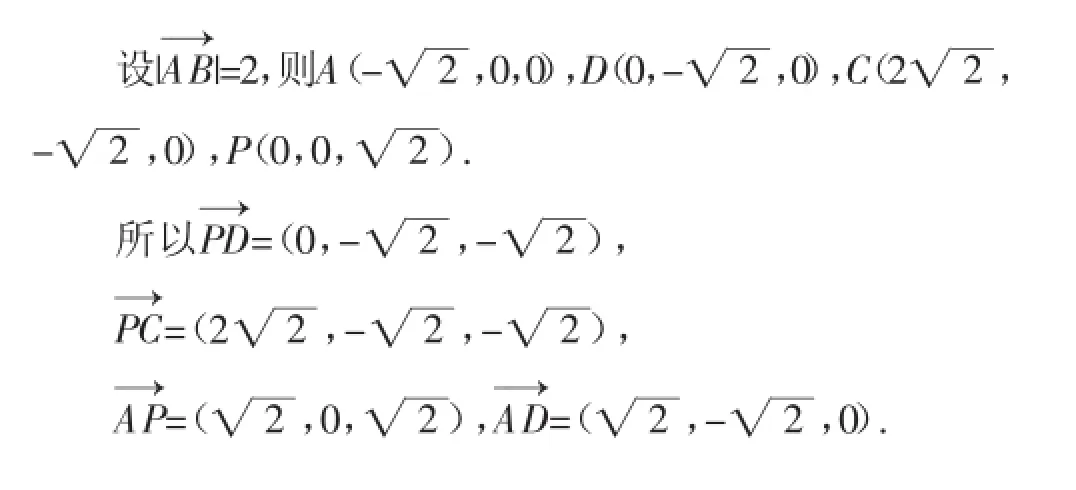
设平面PCD的法向量为n1=（x1，y1，z1），

取y1=-1，得x1=0，z1=1，故n1=（0，-1，1）.

设平面PAD的法向量为n2=（x2，y2，z2），

取x2=1，得y2=1，z2=-1，

故n2=（1，1，-1）.于是

由于〈n1，n2〉等于二面角A-PD-C的平面角，

解法2：由（1）知，CD⊥PB，CD⊥PO，PB∩PO=P，

故CD⊥平面PBD.

又PD⊂平面PBD，所以CD⊥PD.

如图6，取PD的中点F，PC的中点G，连接FG，

图6

则FG∥CD，FG⊥PD.

连接AF，由△APD为等边三角形可得AF⊥PD.

所以∠AFG为二面角A-PD-C的平面角.

连接AG，EG，则EG∥PB.

又PB⊥AE，所以EG⊥AE.

解法3：由（1）知，二面角C-PD-B为直角，只需要求A-PD-B的大小.下面求二面角A-PD-B的余弦值.如图，取DP的中点为F，BD的中点为O，则由题意知，BD=

所以∠AFO即为二面角A-PD-B的平面角.

由解法2知，∠AOF=π 2.在直角三角形AOF中，，所以二面角C-PD-B的余弦值为

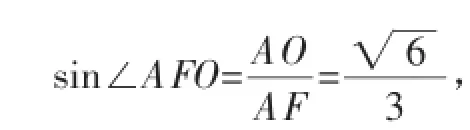
图7

分析：由解法3知，只需求二面角A-PD-B的大小.可以像解法2一样，建系来求.不建系，可不可以利用向量来求呢？

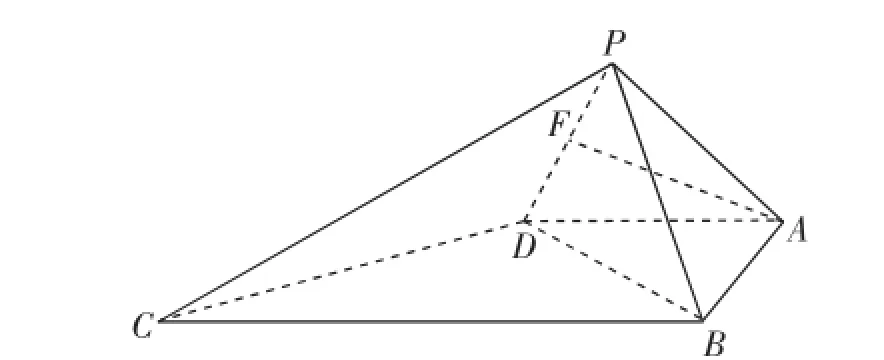
图8