例谈函数恒成立思想解决数列问题*

☉江苏省扬州大学附属中学 吴 琪

例谈函数恒成立思想解决数列问题*

☉江苏省扬州大学附属中学 吴 琪

数列是一类特殊的函数，解决数列问题的视角主要是两个：一是数列本身的视角；二是函数的视角.本文主要探讨类比函数的恒成立问题来解决数列中的恒成立问题、不等式问题等，下面举例说明.

一、解决数列不等式问题

1.利用函数恒成立思想对数列通项放缩

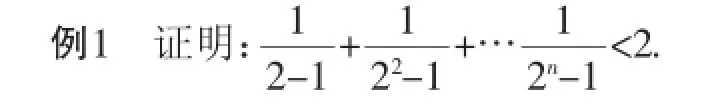
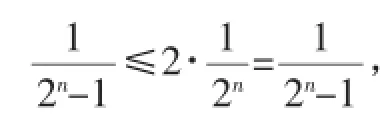
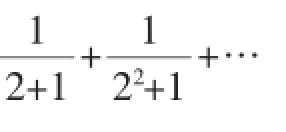
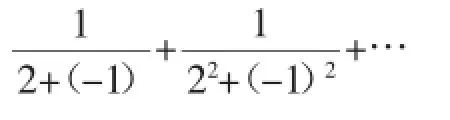
显然是递减数列，故k≥2.

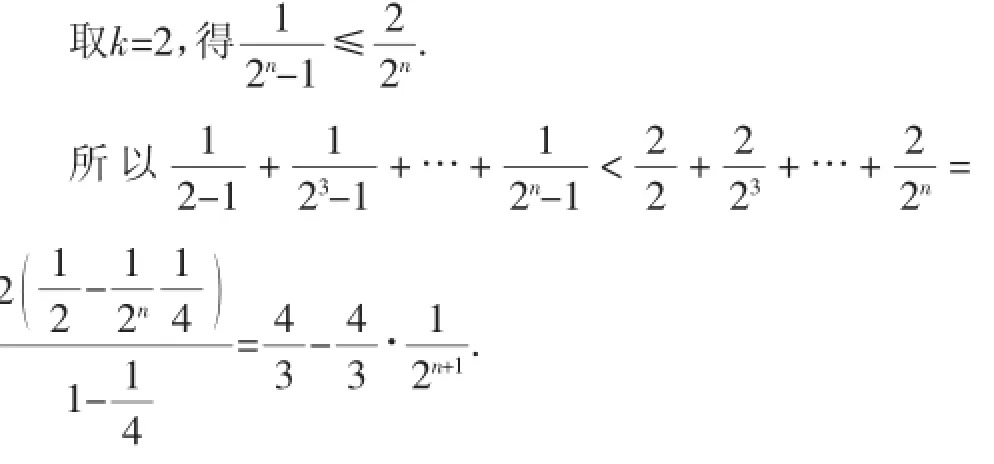
当n→+∞时，bn＜1，且趋向于1，故k≥1，取k=1，得

同理，当n=2m（m∈N*）时，命题也成立.故原不等式得证.

2.利用函数恒成立思想对数列求和后放缩

利用函数恒成立思想，有些时候放缩的误差还是很大，所谓“失之毫厘，谬以千里”，并不能得到所需要的结论，此时可以尝试部分项放缩，即前几项不放缩，从第二项或第三项甚至第四项才开始放缩，从而避免放缩“过犹不及”的缺点.

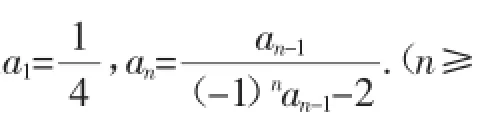
（1）求｛an｝的通项公式an；

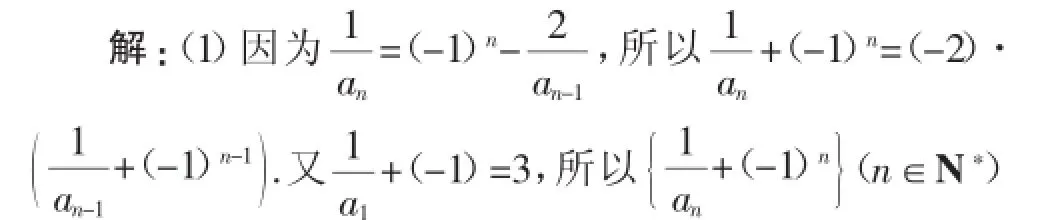
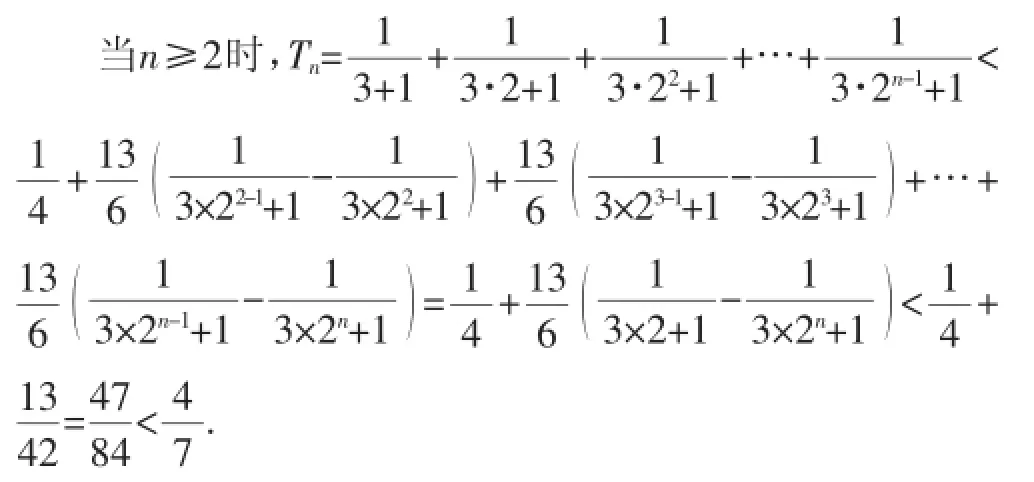
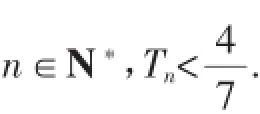
又故对任意的.故原不等式成立.

点评：本题第（2）问的解题思路是将数列通项放缩成等比数列或裂项形式进行求和，再进行放缩，若还不能得到目标结果，可适当对数列通项延后放缩，部分放缩，减少放缩导致的误差.类似的，我们也可以将前面的问题更精确，如将例1中的证明进一步改成放缩延后到第二项，第三项方别得到结论

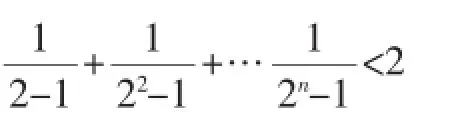
数列不等式是一类综合性较强的问题，我们可以利用函数恒成立思想对数列不等式进行放缩、求解.在解题过程中要充分挖掘题设条件信息，把条件合理的转化、加强、放缩，同时结合问题的结构、形式等特征，使条件与结论建立联系，从而使解题思路通畅.其中合理、恰当的放缩或者部分放缩是能否顺利解题的关键.

二、解决恒成立问题

1.等比数列中的恒成立问题

例3已知数列｛an｝的前n项和为Sn，a1=1且3an+1+2Sn= 3（n为正整数）.

（1）求数列｛an｝的通项公式；

（2）若对于任意的正整数n，k≤Sn恒成立，求实数k的最大值.

分析：（1）根据所给的条件求出公比，确定数列的通项公式；（2）可求出Sn的表达式，结合单调性确定实数k的最大值.

解：（1）3an+1+2Sn=3.①

当n≥2时，3an+2Sn-1=3.②

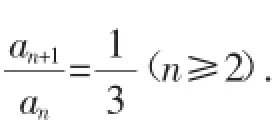
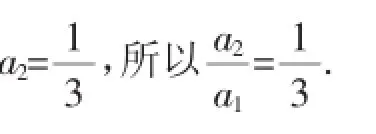
故数列｛an｝是首项为1，公比为的等比数列，所以

2.等差数列中的恒成立问题

例4已知数列｛an｝中，a1=2，a2=3，其前n项和Sn满足Sn+1+Sn-1=2Sn+1，其中n≥2，n∈N*.

（1）求证数列｛an｝为等差数列，并求其通项公式；

（2）设bn=an·2-n，Tn为数列｛bn｝的前n项和，求使Tn＞2的n的取值范围；

（3）设cn=4n+（-1）n-1λ·2an（λ为非零整数，n∈N*），试确定λ的值，使得对任意n∈N*，都有cn+1＞cn成立.

分析：本题的第（3）问，其本质也是恒成立问题，可将通项公式an求出后，问题即可转变为指数函数的单调性问题.

解：（1）由已知，（Sn+1-Sn）-（Sn-Sn-1）=1（n≥2，n∈N*），即an+1-an=1（n≥2，n∈N*），且a2-a1=1.

故数列｛an｝是以a1=2为首项，公差为1的等差数列.所以an=n+1.

所以，当n=1，2时，f（n）＞0，当n≥3时，f（n）＜0，所以n的取值范围为n≥3，且n∈N*.

（3）因为an=n+1，所以cn=4n+（-1）n-1·λ·2n+1，要使cn+1＞cn恒成立，即cn+1-cn=4n+1-4n+（-1）nλ2n+2-（-1）n-1λ2n+1＞0恒成立，所以3×4n-3（-1）n-1λ2n+1＞0恒成立，所以（-1）n-1λ＜2n-1恒成立.

①当n为奇数时，即λ＜2n-1恒成立，当且仅当n=1时，2n-1有最小值为1，故λ＜1.

②当n为偶数时，即λ＞-2n-1恒成立，当且仅当n=2时，-2n-1有最大值-2，故λ＞-2，即-2＜λ＜1.又λ为非零整数，则λ=-1.综上所述：存在λ=-1，使得对任意的n∈N*，都有cn+1＞cn.

点评：对于数列中的恒成立问题，实际则往往是转变为函数的单调性问题，进而转化为数列的最值问题，从而确定参数的取值范围.这里要强调的是，函数的单调性与数列的单调性既有着密切的联系，也有着本质的区别，函数图像一般是连续的光滑曲线，数列图像则是一系列孤立的点，所以如果曲线是单调的，分布在曲线上的孤立点必然也是单调的；但若曲线不单调，分布在曲线上的孤立点未必不单调.所以，称数列是特殊的函数.F

*本文是江苏省教育科学“十三五”规划课题，2016年度重点自筹课题“基于深度学习理念下的数学活动设计研究”的阶段研究成果（课题编号：B—b/2016/02/41）.