一类递推数列的直观解释和“变”题探究

☉安徽省宣城市第二中学 朱长友

一类递推数列的直观解释和“变”题探究

☉安徽省宣城市第二中学 朱长友

一、形如an+1=f（an）递推数列的案例直观解释

我们设想把这类数列的各项（数）用数轴上的点（形）来表示，以例1［1］为例来说明.

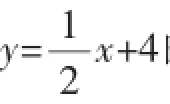
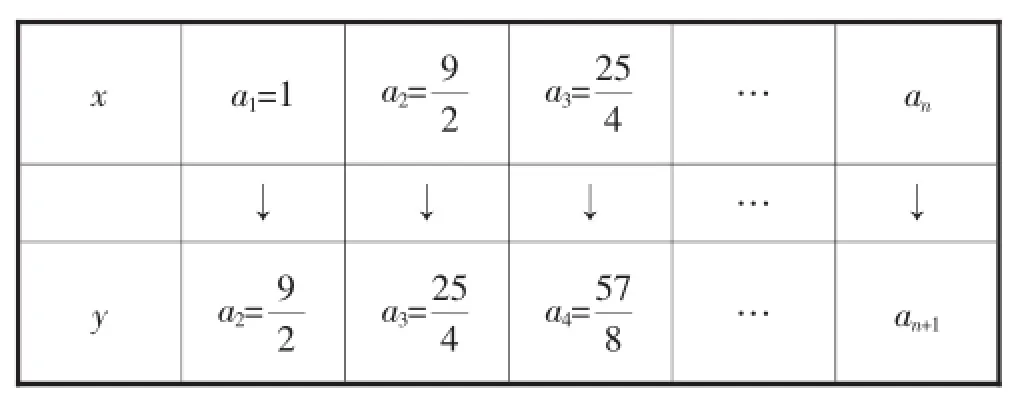
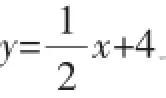
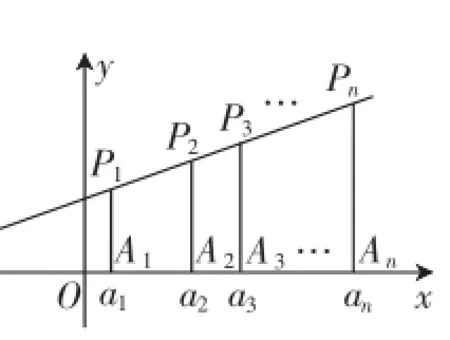
图1

图2

分别过P1，P2，P3，…，Pn引x轴的平行线与y轴交于B2， B3，…，Bn+1，与P2A2，P3A3，…，PnAn，交于Q2，Q3，…，Qn，容易观察到点Q2，Q3，…，Qn，在直线y=x上，如图2.

Q3→P3→…→Pn，可以在直线上得到一排点P1，

P2，P3，…，Pn，从图中看点列P1，Q2，P2，Q3…是“上升阶梯”状，很明显，这些排点是逐渐升高的（形），故｛an｝（数）是单调递增的，通过数形转换，得到此数列的单调性，这就是此类递推数列的直观解释.

从图3中可以看出：点列P1，Q2，P2，Q3，…，Pn是“下降阶梯”状地，故数列｛an｝是递减数列，可以判断，当a1∈R时，数列｛an｝都是递减数列，在解题时，我们可以先判断数列的单调性，然后根据单调性的定义，加以证明.

图3

二、一道高考题的解法探究

（1）｛xn｝为递减数列的充要条件是c＜0；

（2）求c的取值范围，使｛xn｝为递增数列.

分析：本题设计新颖，主要考查形如an+1=f（an）的递推数列的单调性.第（2）问探究c的取值范围，立意深，对考生的探究能力和创新思维有较高的要求.

1.常规解法（读者自己证明，此略）

2.解法探究（利用直观解释）

先利用直观解释探究c的范围，然后加以证明.

当c＜0时，从图4中看到点列P1，Q2，P2，Q3…是“下降阶梯”状，解释了第（1）问，可以判断数列｛an｝是递减函数.

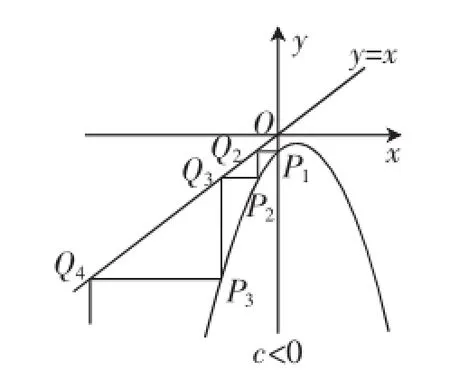
图4

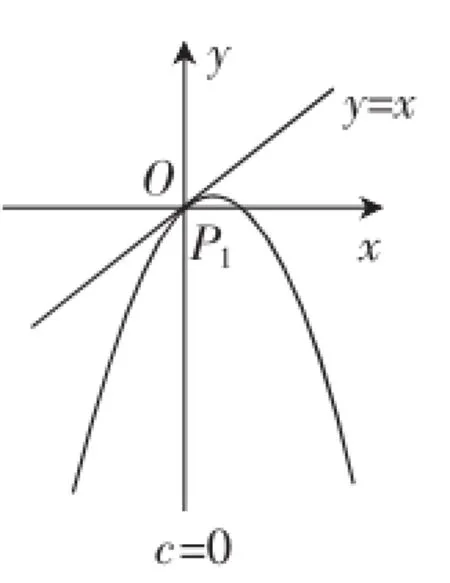
图5

如图5，当c=0时，点列P1，P2，P3，…都重合在坐标原点，故an=0，即｛an｝是常数列.

图6

然后根据数学归纳法证明.（此略）

3.赏析

（1）高等数学的背景.所给的递推数列形如an+1=f（an）的形式，以二次函数为载体，考查数列的单调性，可以看出命题者对初、高等数学教材的理解和感悟非常深刻，反映了命题者的智慧，展现出中学数列知识与后续大学学习的密切联系，体现出“构建共同基础，提供发展平台”的新课程理念.

（2）内蕴厚重，余味无穷.通过本文叙述此类递推数列的直观解释，先探究出c的取值，再根据数学归纳法证明对应的函数是递增函数，根据直观解释，通过改变函数列首项，得到此递推数列的各种不同的单调性，内蕴厚重，耐人寻味.

（3）返璞归真，回归课本.课本在讲解递推数列的单调性时，一般给出的是一个具体的递推数列，而本题给出一个参数c，让我们探究c的取值范围，使它为递增数列，体现了高考中“源于教材，又高于教材”的命题原则，同时实现了平时教学，高考和大学内容的对接.

（4）凸显数学美.该题充分利用数学符号语言，叙述简洁，数列表达式简单，利用直观解释，图形中曲线优美，处处洋溢着数学美，令人赏心悦目！

三、“变”题探究

1.收敛和发散

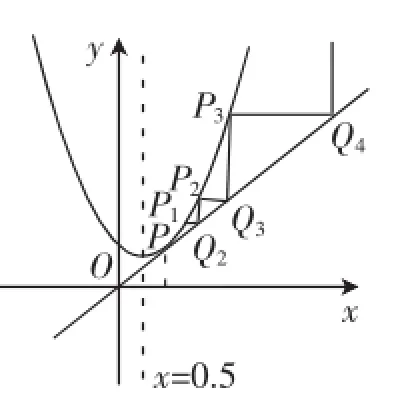
图7

再如：数列｛xn｝由x1＞0，xn+1=确定，画出抛物线y=x2-x+1，它与直线y=x切于点P（1，1）点（如图7），如果x1＞1，点P1，Q2，P2，Q3是“上升阶梯”，所以｛xn｝是单调递增，xn趋于无穷大（此数列是发散的），此数列的极限不存在，当0＜x1＜1，在画出点列P1，P2，P3，…，Pn，这些点列无限趋近于点P（收敛）.

2.影响递推数列an+1=f（an）的单调性的因素

利用递推数列an+1=f（an）的直观解释可以判断影响递推数列an+1=f（an）的单调性的因素有：①数列的首项；②曲线y=f（x）和直线y=x的位置.

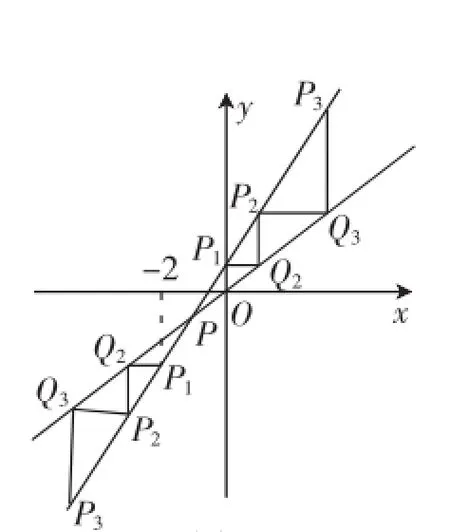
图8

现举例加以分析.

例4试证数列｛an｝满足an+1=2an+1，当a1=0时，是递增数列；当a1=-2时，是递减数列.

分析：用本文的直观解释判断（如图8）.

证明：当a1=0时，（1）当n=1时，a2=2a1+1=1，显然a2＞a1，结论成立.

若假设n=k（k∈N*）时，结论成立，

即ak+1＞ak，

那么n=k+1时

因为ak+2=2ak+1+1，①

ak+1=2ak+1，②

①-②得ak+2-ak+1=2（ak+1-ak）＞0.

所以ak+2＞2ak+1，

这就是说对n∈N*，结论都成立.

所以｛an｝是单调递增数列.

同理证明当a1=-2时，数列是递减的.

显然有x1＜x2，结论成立.

（2）假设n=k（k∈N*）时，结论成立，即xk＜xk+1，

那么n=k+1时，

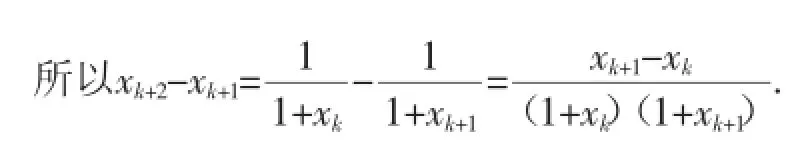
又x1=1，由条件可知xk＞0，所以1+xk＞0，1+xk+1＞0.

由归纳假设知，xk+1-xk＞0，故xk+2＞xk+1.

这就是说，当n=k+1时，结论也成立.

结合（1）（2）得出，数列｛xn｝是单调递增的.

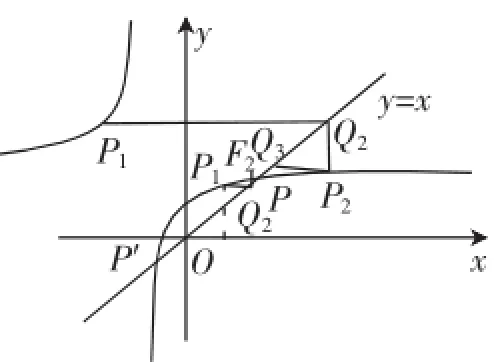
图9

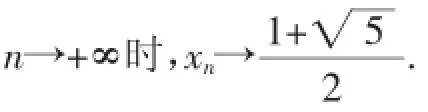
3.大胆“变”题，提升思维的创造性

由图9，可以编出这个递推数列的各种单调性问题：

（4）当x1＜-1时，点列P1，Q2，P2，Q3，…是“下降阶梯”状，是单调递减数列.

只有理解了形如an+1=f（an）递推数列的直观解释，就可以“变”出此类数列的各种单调性问题，对一线教师在教学过程中进行发散式探究的教学起到一定的导向作用.由于篇幅，请读者自己玩味.