复杂网络中重要节点的发现

姜胜文

（四川大学计算机学院，成都 610065）

复杂网络中重要节点的发现

姜胜文

（四川大学计算机学院，成都 610065）

复杂网络中重要节点的发现在实际应用中有着重要意义。重要节点的发现依赖于节点的重要性评估，而如今的一些节点重要性评估参数如介数、度分布、聚类系数等存在适用范围有限、评估结果不够全面等局限性，因为节点在复杂网络中的重要性程度不仅仅只受单一因素的影响。提出一种基于拉普拉斯特征映射算法的节点重要性综合评估方法。这种方法能综合考虑全部节点的局部特征，可以准确地对节点在复杂网络中的重要性程度进行评估，同时能够得到良好的结果。由于该方法无需对复杂网络中所有节点的全部特征进行评估，极大地缩减计算时间，在保证精确性的同时，提高效率，并通过MATLAB仿真与现有算法的结果进行分析对比，证明该算法的有效性和可行性。

复杂网络；重要节点；拉普拉斯特征映射

0 引言

复杂网络的各项基础研究工作中，节点的重要程度评估，重要节点的发掘，具有重要的理论与应用价值[1-2]。国内外在复杂网络重要节点发现研究领域已有诸多成果，对节点的重要性评估方法也有很多，其本质均是源于图论和基于图的数据挖掘，对应于图论中的最关键的节点问题和最关键边问题[3-4]。一般可以通过复杂网络中节点的中心性指标衡量节点的重要性程度，人们经常使用的复杂网络中心性评估指标有介数中心性、特征向量中心性、度中心性、接近中心性等。这些评估指标分别从不同角度描述了每个节点在网络中的重要性程度[5-7]。但现实世界中的复杂网络千变万化、错综复杂，很难只从单一评估指标来评估某个节点在复杂网络中的重要性程度，由于单一指标在不同的网络拓扑结构上的评估具有很大的片面性，复杂网络中每个节点的重要性和这个网络的整体结构相关，需要从多个角度，利用节点的多个重要性指标来进行综合评估[8]。因此本文提出了基于拉普拉斯特征映射算法利用节点的多个指标来进行综合评估，以确定其在复杂网络中的重要程度。因为衡量节点的多个重要性指标对节点进行综合评估能够涵盖影响节点重要性的多种因素，也不再是片面强调某种单一指标的影响，因此能够得到比使用单一指标评估更为精准的节点重要性评估结果。利用该方法对大家普遍使用的 “ARPA网络”数据集的仿真结果表明，此方法能够有效评估与发现复杂网络中的重要节点。

1 拉普拉斯特征映射算法介绍

1.1 算法描述

复杂网络中的节点重要性发现是复杂网络研究各领域的一个基本课题,本节从特征映射角度出发,介绍了一种基于流形学习思想的节点重要性评估算法，即拉普拉斯特征映射算法（Laplacian Eigenmaps，LE）。拉普拉斯特征映射算法[9]是一种非线性降维方法，它将原始数据集映射到低维空间，映射关系分别是X∈Rm×N与Y∈Rd×N，其中m是原始特征维数，d是新特征维数（d〈m），N是数据集的样本个数，原始数据集与映射集中的样本分别是xi∈Rm和yi∈Rd。拉普拉斯特征映射是基于局部保序，能够找到一种映射方式X-〉Y，同时也能保持数据集中的数据在特征空间分布的局部几何属性。它的主要思想是，如果两个数据实例Xi和Xj很相似，那么它们在降维后的目标子空间中应该尽量接近。对于高维空间的点构建连通的无向加权图，再通过求解图拉普拉斯算子的广义特征值实现映射[10]。该算法首先在数据图形中构建 Laplace-Bel-trsmi算子，然后从与 Laplace-Beltrsmi算子相一致的几个最小特征值的特征向量中得出降维后的低维数据集[11]。

1.2 拉普拉斯特征映射算法流程

步骤1构建图 确定每个Xi∈Rm的近邻，并构建邻域关系图G（V，E），如采用KNN算法。

步骤2确定权值

（2）简单方法：在图G（V,E）中，若数据点Xi与Xj相连接，则权重设定为Wij=1，否则，Wij=0。

步骤3特征映射 寻找关系映射Ψ：G（V，E）→Y= {y1，y2，…，Yn-1，yN}⊂Rd，即将邻域加权图 G（V，E）的节点映射为低维欧氏空间Rd中的一组像点Y={y1，y2，…，Yn-1，yN}，然后定义最小化目标函数：

矩阵L叫作图的拉普拉斯矩阵，优化问题则可以写成更简洁的形式：

2 仿真实验

2.1 实验条件与方法

利用大家普遍使用的“APRA网络”拓扑结构[12]（如图1）来分析验证基于拉普拉斯特征映射算法的网络节点重要性多指标多维度的评估方法的正确性。该“APRA网络”拓扑结构为北美常用干线拓扑结构，它由21个节点与26条边组成，根据网络拓扑可得各节点指标数据如下（表1）：

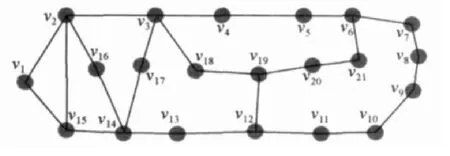
图1 “APRA网络”拓扑

表1 “ARPA网络”各节点的相关指标数据

2.2 实验结果及分析

根据上一节介绍的拉普拉斯特征映射算法，可以计算得出APRA网络中各个节点的得分情况。图2是APRA网各节点相应指标折线对比 （为了更清晰地观察结果，故将相应指标放在两张图里面）。

由图2可以看出，本文介绍的拉普拉斯特征映射算法得到的最重要节点为v3，同时另几种方法得到的结果也为v3（互信息中心性方法与点度中心性中v3和v2得分一样，认为它们在网络中的重要性是相同的），而除了v3之外，拉普拉斯算法认为剩下节点中最重要的5个节点为14，2，19，12，6，而其他几种方法得出的结果也为14，2，12，6，19，说明拉普拉斯算法的结果和其他几种方法的结果是一致的。下面再来看一下拉普拉斯算法与普遍公认的PCA与LDA算法进行对比分析。

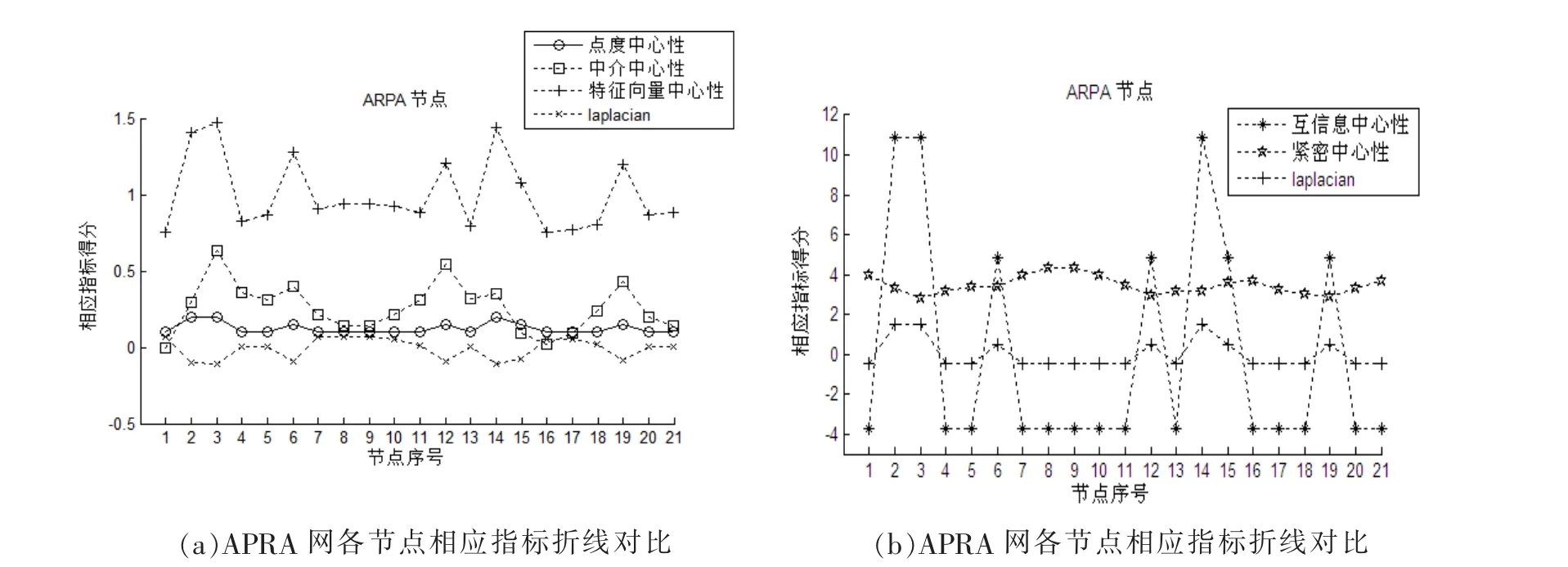
图2

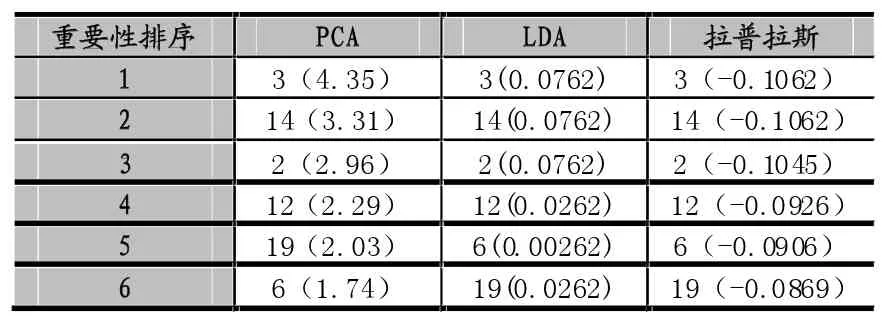
表2 APRA网络三种算法结果对照（前面数值为节点序号，括号内为相对应指标得分）

由表2仍然可以看出，PCA （主成分分析法）和LDA（线性判别分析）以及拉普拉斯算法都认为v3为APRA网络中最重要的节点，其次为v14，v2。同时我们可以观测v19、v12、v16这三个节点，这些节点的LDA得分与点度中心性评分相同，可以认为这三个节点的重要性相同，而根据中介中心性评分指标，认为网络中有更多的节点通过v12这个节点和其他节点进行通信，另外互信息中心性则认为网络中有更多的节点和v6进行通信，较少节点与v19通信；而特征向量中心性认为v6在网络中更受v5、v7、v8、v9这些节点欢迎，因为它们都需要通过v6与网络中其他的节点进行通信。本文提出的复杂网络中重要节点的评估方法综合考虑了以上所有指标，经过客观分析，最终认为v12节点优于v6节点优于v19节点。因此，本文算法结果与其他算法基本一致且更细致合理。由此可见，本文提出的拉普拉斯特征映射方法完全可以用来找出复杂网络中位置重要的节点，并且具有很好的参考价值。

3 结语

节点在复杂网络中的重要程度不应该仅用单一指标来衡量，而需要从多个角度和方面，充分利用节点的多个评估指标来进行综合评估与分析。本文提出了基于拉普拉斯特征映射算法评估复杂网络中节点重要性的方法，此方法综合考虑了每个节点的局部特征，可以准确地对节点在网络中的重要程度进行评估，得到了良好的结果。由于只需对网络中的每个节点的局部属性进行评估，大大缩减了计算时间，在保证精确性的同时，提高了效率。该方法在 “ARPA网络”的仿真实验中，验证了它的可行性与有效性，为进一步分析复杂网络中重要节点的性质，并有效地加以利用奠定了基础。

[1]HE Nan，LI De-Yi，GAN Wen-Yan，ZHU Xi.Mining Vital Nodes in Complex Networks.Computer Science，2007，34（12）:15-16.

[2]张翼.复杂网络节点重要性评估及其应用研究.计算机科学，2011，5:26-28

[3]许进.一种研究系统的新方法-核与核度法[J].系统工程与电子技术，1994（6）:1-10.

[4]P Onnela J，Saramaki J，Kertesz K，Kaski.Intensity and Coherence of Motifs in Weighted Complex Networks[J].Phys Rev.2005.9:34-36.

[5]李鹏翔，任玉晴，席酉民.网络节点（集）重要性的一种度量指标.系统工程，2004，12:56-59.

[6]谭跃进，邓宏钟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践，2006（11）:79-105.

[7]王延庆.基于接连失效的复杂网络节点重要性评估[J].网络安全技术与应用，2008（3）:59-61.

[8]于会，刘尊，李勇军.基于多属性决策的复杂网络节点重要性综合评价方法[J].物理学报，2013（2）:54-62.

[9]Belkin M，Niyogi P.Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering.Advances in Neural Information Processing Systems，2002：1585-592.

[10]姜伟，杨炳儒.基于流形学习的维数约简算法[J].计算机工程，2010（12）:25-27.

[11]毕达天，邱长波，张晗.数据降维技术研究现状及其进展.情报理论与实践，2013，36（2）:125-126.

[12]晋建志.复杂网络基于节点重要性的社团探测及社团演化模型研究.华中师范大学博士论文，2014.5.

Discovery for Important Nodes of Complex Networks

JIANG Sheng-wen
（College of Computer Science，Sichuan University，Chengdu 610065）

In complex networks,it is important how to evaluate the nodes according to their importance.Discovering the important nodes depends on the importance evaluation of nodes.Nowadays most of the existing methods of evaluating pivotal nodes(e.g.betweenness-based,degree distribution,clustering efficient)only think about one factor but not the integration of all complex network in evaluating the importance of nodes,so this methods each can do work in limited application scope.Proposes Laplacian Eigenmaps algorithm to discover the vital nodes in complex networks.In this algorithm,ranking key nodes will consider each node′s integration of whole complex network.After that,it can be accurate to evaluate important degree of the node in the network,and can get a good result.Due to the evaluation does not need calculate whole attribute of complex networks′nodes,so it can greatly reduce the computing time,and the efficiency to discover the key nodes can be improved.Finally,the experiment′s result of MATLAB simulation about the proposed algorithm shows that this algorithm is feasible and effective.

Complex Networks;Key Nodes;Laplacian Eigenmaps

1007-1423（2017）09-0007-05

10.3969/j.issn.1007-1423.2017.09.002

姜胜文（1990-），男，湖北黄冈人，硕士研究生，研究方向为网络与信息安全

2017-02-23

2017-03-15