基于BP神经网络的超磁致作动器建模与控制

王丹梅，冯伟峰

（西南交通大学电气工程学院，成都 611756）

基于BP神经网络的超磁致作动器建模与控制

王丹梅，冯伟峰

（西南交通大学电气工程学院，成都 611756）

超磁致作动器的迟滞非线性是其应用的一大障碍，对此基于BP神经网络建立超磁致作动器GMA的Hammerstein模型，在此模型基础上，设计前馈逆补偿与PID反馈控制相结合的复合控制策略。针对建模范围内的所有单频和复合频率的输入信号，控制器都能保证跟踪控制效果。通过实验实时跟踪的结果进一步验证建模和控制的效果。

迟滞非线性；超磁致作动器；BP神经网络；Hammerstein模型

0 引言

基于磁致稀土，利用其能反应磁场变化作出形变的特性制作而成的执行器，称为超磁致作动器（GMA, Giant Magnetostrictive Actuators），以棒状结构的伸张缩反应磁场变化。由于超磁致作动器储能效率高，远高于镍制品和压电陶瓷，此外响应速度快，能够及时以伸缩反应磁场。因此超磁致作动器常常应用在在微米级别的微位移精确控制领域中。但作动器表现出明显的率相关性，难以得到精确模型、带来控制效果变差等问题。

目前建模方法大致可以分为三种。根据超磁致物理作用机理的物理建模、根据系统输入输出的唯象建模、根据模拟人认知行为的智能方法建模。

对迟滞系统的控制方法，主要有逆补偿控制、不直接求逆以及智能算法等方法，其中逆补偿控制是最主要的方法。在反馈控制策略的研究中，如何使系统使用对象使用不确定性、满足规定性能指标是学者常见研究方向。

1 超磁致作动器的建模与验证

1.1 Hammerstein模型

由于率相关性系统直接建模不容易找到模型描述，本文使用Hammerstein建模思想，把系统拆分两种有成熟控制方法的已知模型，这种方法可以描述大多数非线性系统。其中u、v分别为输入、输出，x是动态线性模块输入。

图1 Hammerstein模型

Hammerstein模型的辨识可把前后两个部分分别进行辨识。本文静态部分采用BP神经网络方法进行辨识，动态部分采用ARX（AutoRegressive eXogenous）模型。

1.2 BP神经网络

神经网络利用函数去逼近模型，属于建模方法的智能方法建模类，通过大量数据的训练过程，可以达到高精度的指标，使神经网络建模方法能够较好地描述超磁致作动器，方便控制。本文采用BP神经网络建立超磁致作动器静态非线性模型。

神经网络只能逼近一对一映射或者多对一映射关系，而作动器的输入与输出之间具有多值映射关系，不能直接用神经网络进行建模，因此本文采用基于扩展输入空间的BP神经网络模型，引入基本迟滞算子对输入空间进行扩展，使神经网络满足一一对应的关系。

图2 扩展空间输入法建立神经网络

1.3 基本迟滞算子

迟滞的多值映射性是其建模的难点之一。本文以不同阈值play算子作为基本单元构造算子[2-8]。

Play算子定义如下：

其中rh表示play算子的阈值。

图3 play算子

PI模型的表达式为：

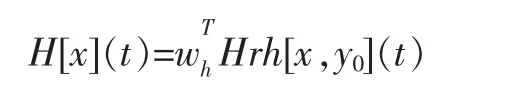
其中wh表示play算子的权重。

算子输出与执行器输出使得模型输入不再是多值，达到一一映射目的。

1.4 ARX模型

自回归各态历经模型是一种有理传递函数模型，广泛用于系统的辨识，可用来描述压电作动器的率相关特性。ARX数学表达式为：

其中ε（t）是误差项，而：

ARX模型传递函数为：

1.5 模型的验证

以均方根误差RMSE（Root Mean Square Error）和相对误差RE（Relative Error）作为检验标准[11]，对建模效果进行定量描述，表达式如下：

如图4给出了不同频率下建模结果与作动器输出的对比图。而误差的RE与RMSE数值见表1。

图4 建模效果验证

表1 建模验证误差

2 跟踪控制策略及效果

2.1 控制器设计

控制系统结合Hammerstein分为两部分，以传统控制方法解决系统本身具有的复杂非线性构成。第一部分逆补偿控制，抵消非线性的影响。第二部分PID控制器，弥补开环逆补偿控制易受扰动等影响，校正系统的误差。将两者结合既可稳定性又可提高跟踪性能，而且能够达到实时控制的效果。

图5 跟踪控制器框图

r和y分别为输入信号和输出信号，NN和NN-1为基于基本迟滞算子EHO构建的BP神经网络模型及其逆模型，L为基于ARX建立的线性动态部分，为线性部分的近似逆，G为前馈补偿器。

ARX辨识结果有：

因为L是严格正则的，不能直接求逆，取一个近似逆：

2.2 实时跟踪控制实验

实时跟踪控制实验，如图6所示。实验中所用器材包括半实物仿真平台dSPACE、上位机、超磁致作动器、GF-20型功率放大器等。首先在上位机中设计好控制程序，下载至dSPACE后，经功率放大器放大后作用于作动器。以电涡流传感器（灵敏度8mv/μm）测得超磁致作动器的位移信号，回传给dSPACE，最后在上位机中进行数据分析和处理。

图6 实时跟踪实验

根据设计好的控制策略，使超磁致作动器跟踪1-200Hz范围内的参考信号，包括单频率和复合频率。

图7给出了几组跟踪效果对比图，表2详细给出了多种频率输入信号跟踪控制的均方根误差和相对误差。

表2 跟踪控制误差

3 结语

本文以超磁致作动器（GMA）为研究对象，基于BP神经网络建立了0-200Hz内的Hammerstein模型[1]，并基于此模型设计了逆补偿结合PID控制的跟踪控制器。实验结果显示，该模型和控制器对单频和复合频率的输入信号都适用。实时跟踪实验验证了上述模型，能够有效跟踪不同频率，包括复合频率的信号。控制效果的均方根误差小于0.5μm，相对误差小于4.7%。

[1]毛剑琴.智能结构动力学与控制[M].科学出版社，2013.

[2]谷国迎.压电陶瓷驱动微位移平台的磁滞补偿控制理论和方法研究[D].上海交通大学，2012.

[3]Knohl T，Unbehauen H.Adaptive Position Control of Electrohydraulic Servo Systems Using ANN[J].Mechatronics，2000，10（1-2）: 127-143.

[4]柳萍，毛剑琴，张伟，等.基于Hammerstein-like模型的超磁致伸缩作动器建模与控制[J].北京航空航天大学学报，2013，39（7）：17-921.

[5]毛剑琴，岳玉芳，张建刚，等.复杂系统模糊建模的模糊树方法[J].控制理论与应用，2002，19（2）:153-156.

[6]Tao G，Kokotovic P V.Adaptive Control of Plants with Unknown Hysteresis[J].IEEE Transactions on Automatic Control，1995，40（2）：200-212.

[7]Liu J，Zhou K.Neural Networks Based Modeling and Robust Control of Hysteresis[C]Control Conference（CCC），2016 35th Chinese. TCCT，2016:3051-3056.

[8]Giri F.Block-Oriented Nonlinear System Identification[M].Berlin:Springer，2010.

[9]Zhao X，Tan Y.Modeling Hysteresis and Its Inverse Model Using Neural Networks Based on Expanded Input Space Method[J].IEEE Transactions on Control Systems Technology，2008，16（3）:484-490.

[10]Kuhnen K.Modeling，Identification and Compensation of Complex Hysteretic Nonlinearities:A Modified Prandtl-Ishlinskii Approach [J].European journal of control，2003，9（4）:407-418.

[11]范家华，周攀，郝兵兵，等.基于BP神经网络的压电作动器建模与控制[J].现代计算机，2016（8）:35-39.

Modeling and Control of Giant Magnetostrictive Actuators Based on BP Neural Network

WANG Dan-mei，FENG Wei-feng
（College of Electrical Engineering，Southwest Jiaotong University，Chengdu 611756）

The hysteresis nonlinearity of the GMA is a major obstacle in the application of such material in actuators.Establishes a Hammerstein model based on the BP neural network to model the hysteresis nonlinearity.Based on the model,designs a composite control strategy combining feed-forward compensation and PID feedback control.The controller ensures tracking control for all single and complex frequency input signals within the modeling range.Finally,the results of the real-time tracking experiment on GMA further validate the modeling and control results.

Hysteresis Nonlinearity;Giant Magnetostrictive Actuators;BP Neural Network;Hammerstein Model

国家自然科学基金重点项目（No.61433011）

1007-1423（2017）09-0011-05

10.3969/j.issn.1007-1423.2017.09.003

王丹梅（1992-），女，四川资阳人，硕士研究生，研究方向为迟滞非线性系统建模与控制

2017-02-17

2017-03-10

冯伟峰（1991-），男，广东佛山人，硕士研究生，研究方向为机器人控制