木质穿孔板结构的吸声性能

侯清泉，郭明辉

(1.黑龙江科技大学 机械工程学院，哈尔滨 150022；2.东北林业大学 生物质材料科学与技术教育部重点实验室，哈尔滨 150040)

木质穿孔板结构的吸声性能

侯清泉1，郭明辉2

(1.黑龙江科技大学 机械工程学院，哈尔滨 150022；2.东北林业大学 生物质材料科学与技术教育部重点实验室，哈尔滨 150040)

为避免木质穿孔板结构吸声性能繁琐的实验测试，采用有限元法对中密度木纤维穿孔板进行声学分析。结果表明：声压分布云图显示在有限元模型的扬声器和被测材料间形成了多个峰、谷交替存在的声压分布区，且模拟结果与实际测试结果相符。算例分析得到各频率点模拟与实验吸声系数的总误差为3.12%，验证了有限元软件ANSYS应用于木质穿孔板结构吸声性能分析的可行性，为设计声学性能优异的穿孔板吸声结构提供参考依据。

木质穿孔板；有限元法；ANSYS；声学分析; 驻波管

0 引 言

为创造出理想舒适的音质环境或是控制环境噪声，当今建筑多采用木质穿孔板吸声结构。目前，木质穿孔板结构的吸声性能需在实验室采用驻波管法或混响室法对实物进行测定，测试极不方便，研发周期长，与此同时必然导致人力、物力和财力的浪费。有限元法具有省时省力、节约研发成本、各结构参数修改方便等优点。近年来，一些科研院所和高校进行了仿真计算方法和声学测试方面的研究[1-2]，同时对穿孔板结构进行数值模拟分析[3-4]，国外学者则对穿孔板设计进行研究[5-6]。但未见应用有限元软件ANSYS进行木质穿孔板吸声性能的研究。因此，文中以中密度木纤维穿孔板为研究对象，借助有限元软件ANSYS来分析穿孔板结构的吸声性能，以期为设计和制造声学性能优异的穿孔板吸声结构提供数据支持。

1 穿孔板理论

穿孔板每个穿孔及穿孔正对着的后部空气柱的共同作用类似于亥姆霍兹共振器，穿孔板吸声结构可理解为众多并联方式连接的亥姆霍兹共振器。声音进入穿孔板的孔之后便使板后空腔内的空气振动起来，若该声音频率与结构固有属性之一的共振频率相同时，腔内的空气将发生共振，会使声音所携带的能量更多地转化为热能，从而起到高效率的吸声作用[7]。

穿孔板的声阻抗率比为

Zs=Ra+jωMa,

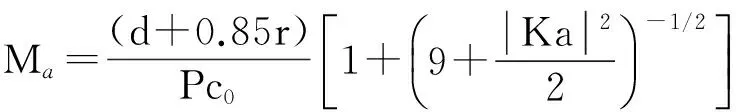
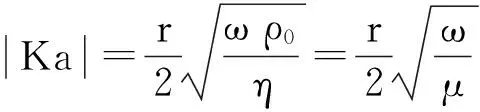
式中:Ra——相对声阻,量纲为1；

Ma——相对声质量，s；

ω——角频率,rad/s；

μ——空气的运动粘性系数,m2/s；

d——穿孔板板厚,mm；

P——穿孔率,%；

c0——声速，20 ℃时，c0=344 m/s；

r——穿孔孔径,mm；

η——空气的动力粘性系数，20 ℃时，空气的动力粘性系数η=1.89×10-5Pa·s；

ρ0——空气密度，20 ℃时，ρ0=1.21kg/m3。

穿孔板吸声结构为共振吸声结构，可通过其等效电路来得到吸声相关特性。穿孔板后腔体的声阻抗率比为

Z′s=-jcot(ωh/c0)，

其中，h为空腔深度。垂直入射时的吸声系数为

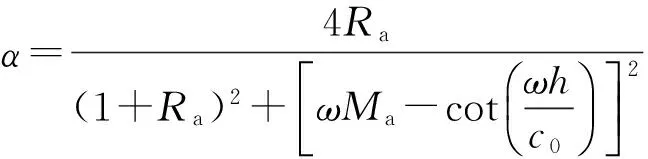
吸声系数α在共振时达到最大：

影响穿孔板结构吸声性能的因素有很多，主要包括穿孔板板厚d、穿孔孔径r、穿孔率P及板后空腔深度h等因素[8]。

2 仿真模型

2.1 模块选取

软件ANSYS的Multiphysics和Mechanical模块中有声学分析的功能，可在流体中研究声音的生成、传播、吸收和反射等问题。耦合声场分析需考虑流体介质—固体结构间的相互影响和相互作用，一般来说需对流体介质自身及与之相接触的固体结构建立有限元模型。而非耦合声场分析只考虑流体介质自身即可。许多的声学问题可以采用谐波响应分析来求解，分析得出流体介质—固体结构交界面上的压力分布。通过限定载荷的频率范围，可以获得不同频率时的压力分布。

ANSYS软件中声场分析功能模块有四种类型的单元可选，二维模型的流体使用Fluid29单元，三维模型的流体介质采用Fluid30单元，Fluid129和Fluid130单元则是用来构建包围Fluid29和Fluid30单元的无限外部壳体。这四种单元类型完全可以构建出流体介质的所有模型。并且软件规定仅Fluid29和Fluid30单元可与固体结构单元相接触；而Fluid129单元只能接触Fluid29单元，Fluid130单元只能接触Fluid30单元，Fluid129和Fluid130单元都不可以与固体结构单元直接接触。文中的仿真分析是在Mechanical模块中进行的，选用的是Fluid30和Fluid130单元。

2.2 模型建立

为检验穿孔板结构吸声特性有限元模拟方法的有效性和可靠性，需要把模拟得出的结果与实验测试结果进行比较，因此有限元模型就按照驻波管的结构形式和尺寸来设定。实验用驻波管为杭州爱华生产的AWA6122A型(图1)，其关键硬件组成部分为配套电脑、探测小车、安放测试材料的被测材料管和一根内壁光滑的等径驻波管，软件部分为配套电脑中用于控制音频振荡器发声频率和采集声压处理及显示的相关软件。穿孔板后空腔深度的调整通过刚性活塞的移动来实现。

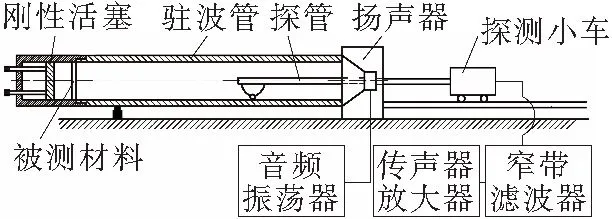
图1 驻波管结构

据国标GB/T11718—1999《中密度纤维板》，穿孔中密度木纤维板的弹性模量取为2.7×109Pa，密度取为500kg/m3。 泊松比的数值根据文献[9]取0.26。

建立木质穿孔板模型时，首先建出高度为板厚的圆柱体，为打孔前纤维板模型。根据设计在该板对应位置处建立直径等于穿孔孔径的圆柱，再经布尔运算将板子加工成穿孔板。应注意加工孔所用圆柱的高度一定要比板厚大，否则将提示错误，使在板子上穿孔无法进行。

AWA6122A型驻波管扬声器的声功率为10W，加载阶段，需要在声源所处在的几何面上施加声压载荷，故需进行声功率W与声压p之间的换算：

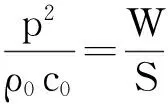
(1)

式中：S——声能穿过的横截面积,m2。

实验测试所用驻波管管径D为96 mm，可计算出管的截面积S。然后把W、S和ρ0c0的数据代入式(1)，求得声压为p=757.4 Pa。故在有限元模型的定义载荷阶段，音箱所在的几何面上施加面载荷即声压值为757.4 Pa。

3 结果与分析

从扬声器传出来的特定频率声波在驻波管中将以平面波的形式向被测试材料端传播，于理论层面可以证明，当管子中声音频率与管子几何尺寸满足式(2)时，声波是沿管子轴线方向传播的平面波。

对于文中穿孔板测试所用的圆管式驻波管：

f<(1.84/π)×(c/D)。

(2)

被测试材料的表面将平面波反射回去，在光滑的管子中建立起驻波声场，从被测试材料表面算起管中将出现声压极大值和极小值交替变化的情况。

结构参数为孔径r=8 mm,穿孔率P=6%,空腔深度h=50 mm的木质穿孔板吸声声压云图整体效果如图2所示。由图2可知，ANSYS软件[10]可用于木质穿孔板结构的吸声性能研究。在有限元模型的扬声器和被测材料或吸声结构间出现多个峰、谷依交替规律变化的声压分布区，当扬声器处施加频率f为2 kHz的声音时，甚至在穿孔板的后方也出现了一个波谷。穿孔板峰、谷的出现组数直接取决于所施加声音的频率。低频时声波的波长长，所以波谷的出现次数就少，这与驻波管实测一致。当用驻波管对穿孔板进行吸声性能测试时，测试者沿导轨缓慢且细心地推动探测小车，小车携探管自扬声器侧移向被测材料端时，高频声声源情况下可采集并测到许多组的声压级波峰、波谷值。一旦声源频率降至125 Hz的低频时，实验设备仅能保证测到一组声压级的波峰、波谷值。从声压分布云图上可见，对于确定的声源声音频率，两个波谷之间的间距是相同的，在波谷的附近声压发生着连续变化。

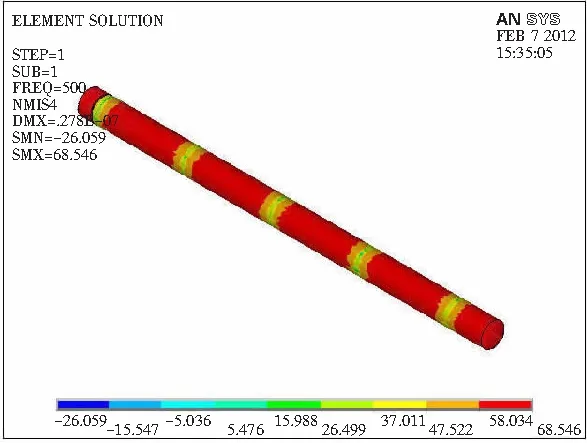
a f=500 Hz

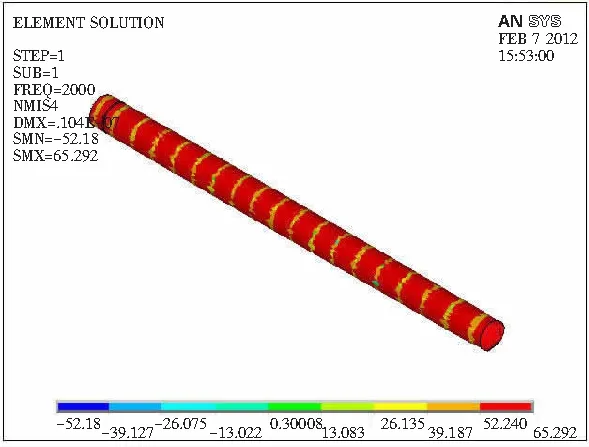
b f=2 000 Hz

4 算 例

木质穿孔板吸声结构的参数组合为孔径r=8.6 mm、穿孔率P=5.6 %、板厚d=16 mm、空腔深度h=100 mm。对于这样大厚度的中密度木质纤维板，其穿孔只能采用木工钻床来进行加工。试件网格划分后的有限元模型如图3所示。

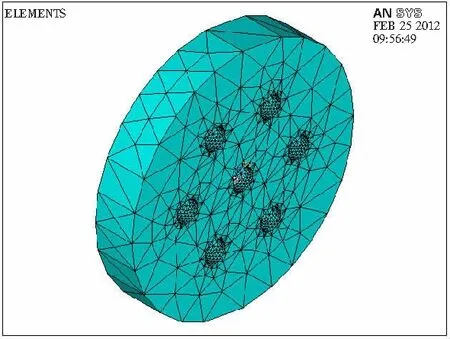
图3 试件有限元模型Fig.3 Specimen FEM model

仿真结果在不同频率点波谷处的部分放大图见图4，可以看出波谷处代表更低声压级的颜色出现的范围很小，故该颜色所代表的声压级不具典型性，必须人为研判从而找出波谷处声压级的主要分布情况，然后读出该颜色所代表的声压级最小值，这其中就加入了人的主观因素。

由仿真结果经过分析将各频率点的声压级最大值Lmax和最小值Lmin填入表1。

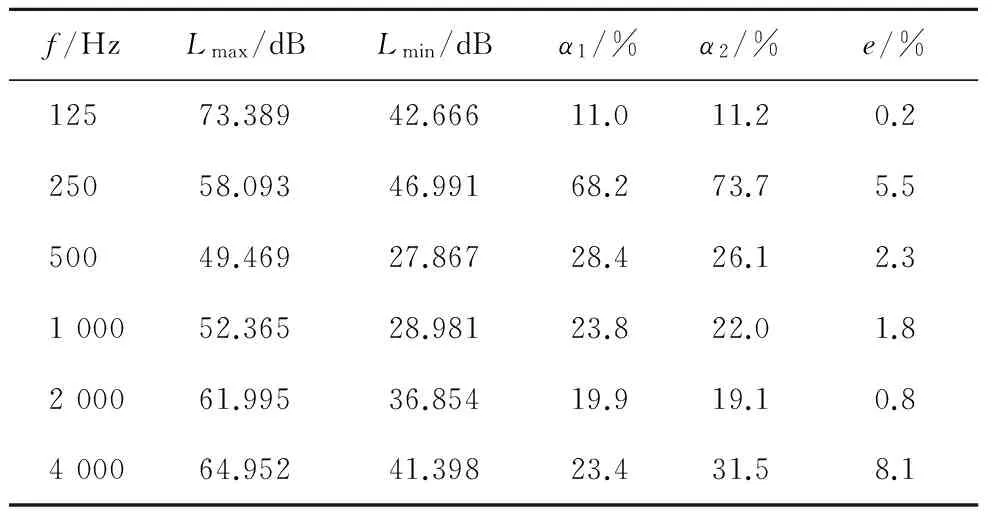
表1 各频率点吸声系数对比及误差Table 1 Sound absorption ratio and error at certain of frequencies

由表1中数据可以看出，频率250 Hz时吸声效果达到峰值，实验测得的吸声系数α2高达0.737，低频时吸声效果好，是因为算例穿孔板板厚达到d=16 mm，这说明增加穿孔板的厚度，确实有助于提高吸声结构的低频吸声能力。随着板厚的增加，吸收峰将向低频侧发生偏移。将各频率点声压级差值代入式(3)求出模拟吸声系数：

(3)

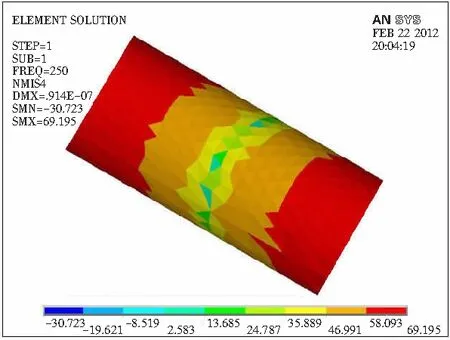
a f=250 Hz

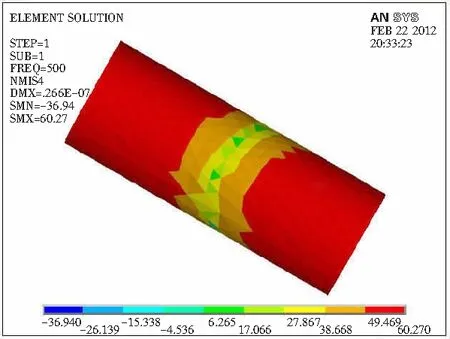
b f=500 Hz

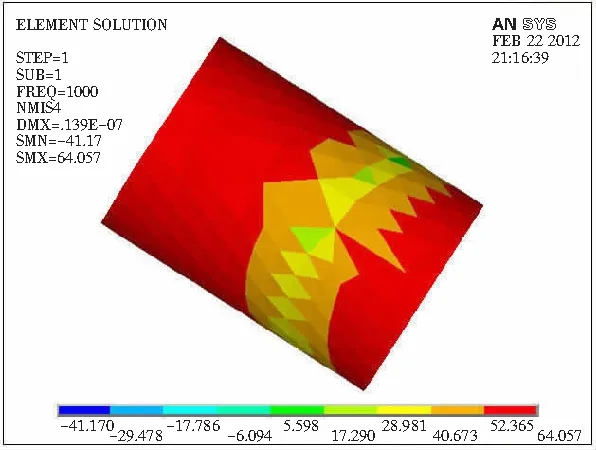
c f=1 000 Hz

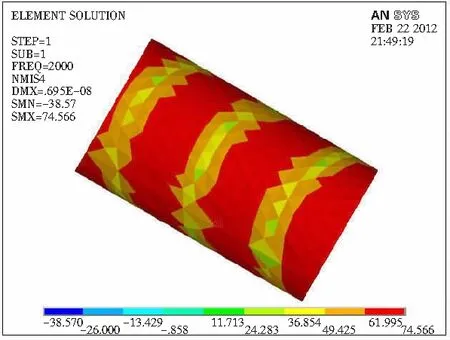
d f=2 000 Hz

将各频率点模拟吸声系数和实验吸声系数代入式(4)来求得模拟误差e，其平均值仅为3.12%。由表1中模拟吸声系数与实验吸声系数的误差可知，该算例的ANSYS软件模拟吸声系数与驻波管测试得到的吸声系数非常接近，在个别频率点上相差很小，从而进一步证实了文中采用有限元法分析木质穿孔板吸声特性的可行性和所建有限元模型的可靠性。

e=|α1-α2|。

(4)

5 结 论

(1)ANSYS软件可用于分析木质穿孔板结构的吸声性能，在有限元模型的扬声器和被测材料或吸声结构间形成多个波峰、波谷按间隔规律出现的声压分布区。高频声的波长短，会有多组峰谷，这与驻波管实测过程一致。从声压分布云图可见，波谷处的声压连续变化。

(2)将ANSYS软件模拟得到的吸声系数与实验吸声系数进行对比，各频率点的总误差为3.12%。证明了研究中采用有限元分析方法的正确性和有限元模型的可靠性。在已建立的有限元模型基础上，只需单独或组合地调整模型结构参数，即可用于其他不同结构和具体参数的木质穿孔板结构的吸声性能分析，简单方便。

[1] 杜 韬，苗天丞，付国涛，等．微穿孔板吸声结构仿真计算方法研究[J]．工程热物理学报，2015,36(6)： 1242-1246.

[2] 吕金磊，彭 强，王海锋．管道中微穿孔板吸声结构声学性能测试与分析[J]．噪声与振动控制，2016，36(1)： 200-203.

[3] 孙文娟，孔德义，尤 晖，等．微穿孔板吸声体声学性能的仿真研究[J]．仪表技术，2012(3): 10-13,16.

[4] 宁玉恒，杨 丹．穿孔板声特性的数值模拟和试验研究[J]．制造业自动化，2014,36(8)： 64-67.

[5] Bolt R H.On the design of perforated facings for acoustic materials[J]．J Acoust Soc Am,1947，19: 917-921.

[6] Ingard K U,Bolt R H.Absorption characteristics of acoustic material with perforated facings[J]．J Acoust Soc Am,1951,23: 533-540.

[7] 左言言，周晋花，刘海波，等．穿孔板吸声结构的吸声性能及其应用[J]．中国机械工程,2007，18(7)： 778-780.

[8] 马大猷.现代声学理论基础[M].北京: 科学出版社,2004.

[9] Sekino N,Sasaki T.Poisson’s ratio of wood-based panels and poisson’s effect of hygroscopic linear expansion under a uniaxially dimensional restraint[J].Journal of the Society of Materials Science,2004,53(4): 396-401.

[10] 侯清泉．木质穿孔板结构的吸声性能及模拟仿真研究[D]．哈尔滨： 东北林业大学，2012.

(编校 王 冬)

Performance of wooden perforated panel absorption structure

HouQingquan1，GuoMinghui2

(1.School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China；2.Key Laboratory of Bio-based Material Science & Technology of Ministry of Education, Northeast Forestry University,Harbin 150040,China)

This paper is a response to a more complex test process of wooden perforated panel acoustical absorption structure’s performance by adopting finite element method.The result shows that there are some pressure distribution zones behaving with peak and valley alternation between loudspeaker and the tested material of the finite element model,and the simulation coincides with test result of experiment equipment.The total error of 3.12% between frequency points of simulation and experimental absorption coefficient,as calculated,verifies the feasibility of applying finite element software ANSYS for analyzing wooden perforated panel acoustical absorption structure’s performance.The study may provide a reference for the perforated panel sound absorption structure with excellent acoustic performance.

wooden perforated panel; finite element method; ANSYS; acoustical analysis; standing wave tube

2017-02-22

黑龙江省教育厅科学技术研究项目(12521482)；林业科学技术推广项目([2015]10号)

侯清泉(1975-)，男，内蒙古自治区阿荣旗人，副教授，博士，研究方向: 机械设计、CAE技术、振动噪声控制，E-mail：houqingquan@usth.edu.cn。

10.3969/j.issn.2095-7262.2017.02.020

TB535.1

2095-7262(2017)02-0192-04

A