采煤机扭矩轴扭断参数的神经网络算法辨识

万 丰,蔡桂英

(1.黑龙江科技大学 机械工程学院,哈尔滨 150022; 2.黑龙江科技大学 计算机与信息工程学院，哈尔滨 150022)

采煤机扭矩轴扭断参数的神经网络算法辨识

万 丰1,蔡桂英2

(1.黑龙江科技大学 机械工程学院,哈尔滨 150022; 2.黑龙江科技大学 计算机与信息工程学院，哈尔滨 150022)

针对实际工况下采煤机扭矩轴工作性能不稳定的问题，提出基于Hopfield神经网络的辨识算法来优化扭矩轴参数。利用该算法拟合采煤机扭矩轴的实验数据，并以该数据为样本，辨识采煤机扭矩轴参数，应用MATLAB软件比较分析实验与仿真的误差。结果表明，基于Hopfield神经网络的辨识算法对采煤机扭矩轴传动系统建模工作量小、通用性好，且仿真误差小于1 N·m，可应用于实际工程。

采煤机；扭矩轴；Hopfield神经网络；刚度；系统辨识

0 引 言

滚筒式采煤机的工作环境恶劣，工况复杂多变，造成了其负载易产生波动和突变，极易对其传动系统零部件产生冲击及瞬时过负荷，其中，采煤机扭矩轴作为传动系统电机轴，或传动链初级的联接轴，可以很好地保护主传动系统零部件免于突加负载的冲击，由于在结构上采取了剪切槽，并可起到过载保护的功能[1-4]。这样的工况条件及结构特点，要求采煤机扭矩轴既有一定的刚度，又要有一定的弹性，从而在过负载条件下达到保护的目的。但采煤机扭矩轴材料选择以及热处理工艺的复杂性，使其在工程应用中工作性能不稳定[5-10]。

Hopfield神经网络是参数化的辨识方法，对于连续动态系统，利用Hopfield网络可以直接估计队形或过程的数学模型参数，其利用准则是均方误差准则[11]。因此，笔者从Hopfield动态数学模型出发，根据滚筒式采煤机截割部传动系统运动方程，以及采煤机扭矩轴材料力学模型的特点，提出了基于Hopfield神经网络的系统辨识算法，并借助MATLAB软件对该算法进行建模与仿真，以期找到采煤机扭矩轴理想参数的估计方法，优化采煤机扭矩轴设计。

1 Hopfield网络模型及系统辨识算法

1.1 Hopfield网络模型

从结构上来说，Hopfield网络是全互联的单层反馈型神经网络，连续型的Hopfield网络中每个神经元的动态特性可表述为：

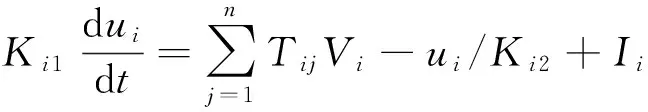
(1)

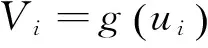
式中：ui——第i个神经元的输入；

Vi——第i个神经元的输出；

Tij——第j个神经元到第i个神经元之间的连接权；

Ii——偏置输入；

Ki1、Ki2——系统实现非线性元件时的线性元件；

针对含有n个神经元的Hopfield网络，可有以下的能量函数：

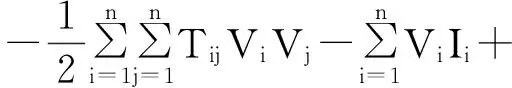
假定加权矩阵T为对称矩阵(Tij=Tji),g-1(u)单调上升，则有：

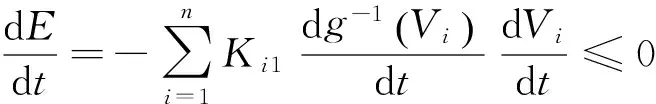
(2)

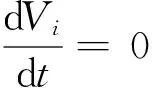
式(2)表明，计算能量函数E具有负的时间梯度。随着时间的变化，网络状态方程式(1)的解总是朝着使系统计算能量减少的方向运动，网络的平衡点就是E的极小点。

1.2 辨识算法

基于Hopfield网络的辨识为参数化辨识方法，使用的准则为均方误差准则。设待辨识对象为可由状态空间形式描述的线性系统：

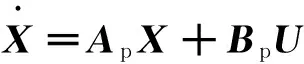
式中：Ap、Bp——未知矩阵；

X——系统状态；

U——系统输入。

定义辨识模型为以下微分方程：

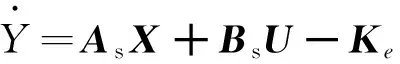
(3)

e=X-Y。

则有误差满足动态方程：

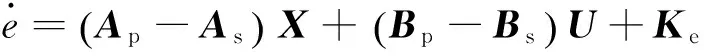
将式(3)的系统矩阵As、Bs作为Hopfield网络的神经元输出，优化目标是使误差e达到极小。由上述可得到基于Hopfield网络的系统辨识框图，如图1所示。

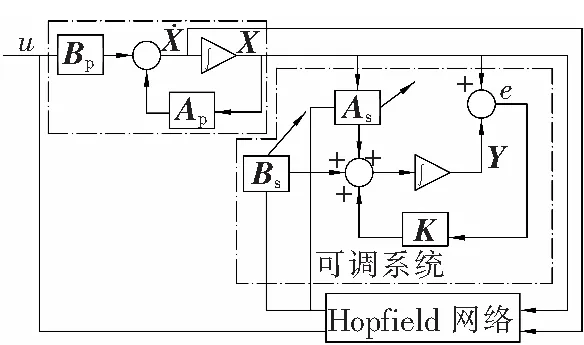
图1 基于Hopfield网络系统辨识框图Fig.1 System identification based on Hopfield network diagram

为了保证As和Bs有递归关系，设定能量函数E仅与参数误差有关：

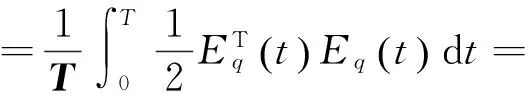
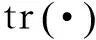
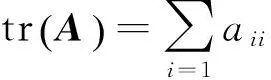
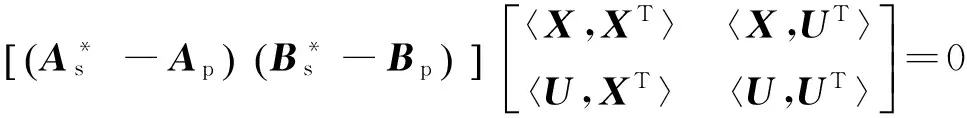
对于确定Hopfield网络的加权矩阵T和偏置输入I，将计算能量函数写成下式：

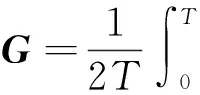
(4)

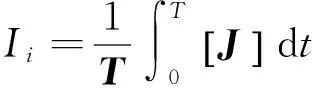
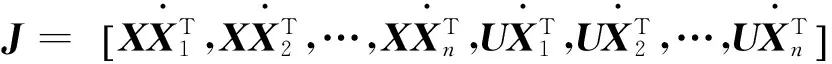
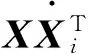
2 采煤机扭矩轴传动系统辨识

依据等效原则，采煤机扭矩轴传动系统可以用二质量单自由度传动系统模型等效计算。

由动力学拉格朗日方程可得到系统运动微分方程：

(5)

式中:J0、Je——电机转子、传动系统齿轮等效转动惯量，kg·m2；

M1、M2——截割驱动电机转矩，采煤机工作机构负载转矩，N·m；

φ1、φ2——电机转子角位移，采煤机工作机构角位移，rad/s；

ke——采煤机扭矩轴刚度。

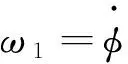
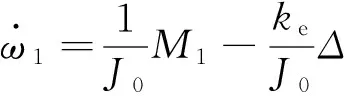
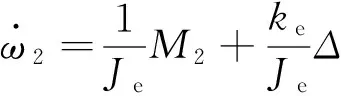
根据动力学原理，可显见：

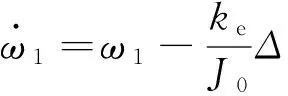
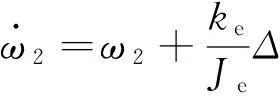
(6)

下面，仅针对工作机构方程建立Hopfield神经网络辨识，取式(6)可得：

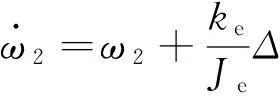
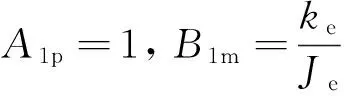
取辨识网络为：

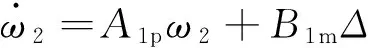
此时，A1s、B1s为Hopfield网络神经元输出。由式(4)可得到二阶Hopfield网络的加权系数和偏置输入分别为

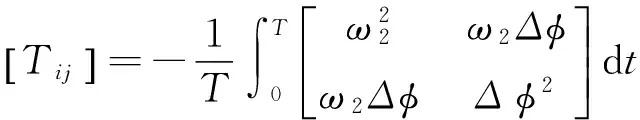
(7)

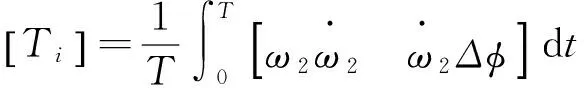
(8)

3 实验与仿真

3.1 破坏实验

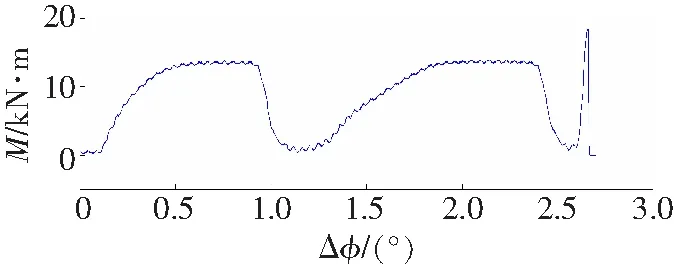
以滚筒式采煤机电机额定功率500 kW应用的扭矩轴参数，选用40Cr设计加工被试工件，分别采用瞬态快速加、稳态慢速、震荡三种加载方式，对工件进行破坏性实验，分别记录加载扭矩、角位移，将每个试件的实验数据分别导入MATLAB软件中进行曲线拟合，拟合出扭矩——转角差曲线，如图2所示。

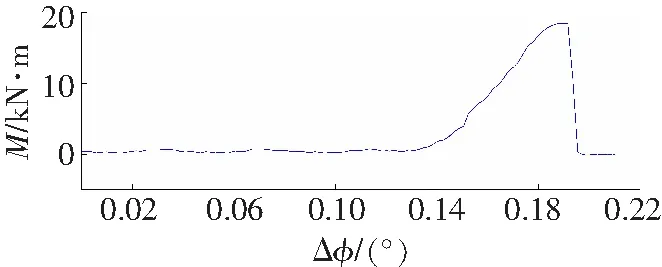
a 试件1

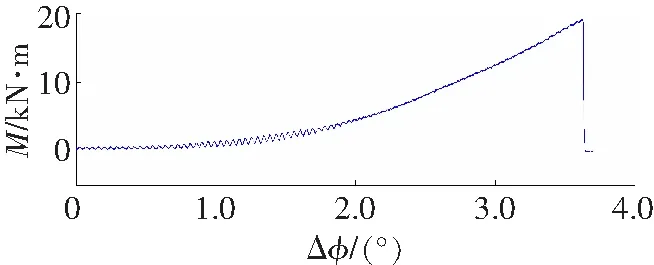
b 试件2

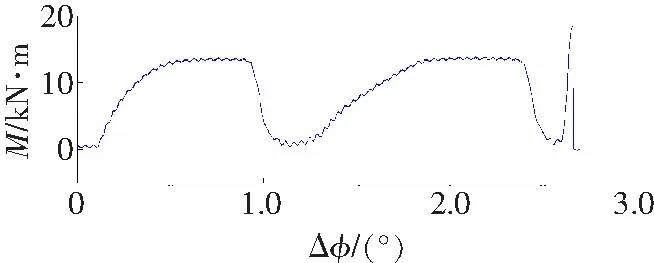
c 试件3

3.2 仿真分析

利用式(7)、(8)建立Hopfield神经网络，采用MATLAB软件对被试件进行仿真，仿真程序利用MATLAB提供的神经网络工具编写。训练及测试以破坏实验三种加载方式实验数据为样本，并检验网络的泛化能力，设定期望均方误差为10-4,最大训练次数为1 500次。仿真结果如图3所示。

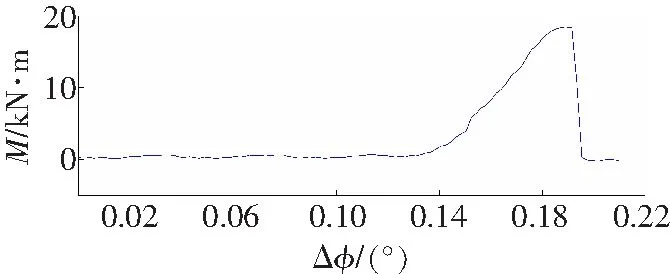
a 试件1

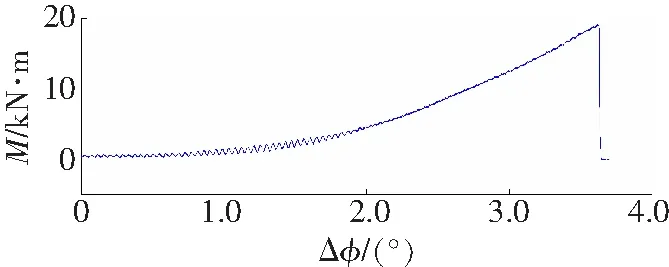
b 试件2

c 试件3

样本训练过程中以样本点目标值的逼近作为程序的收敛条件。因此，凡是成功的训练，训练样本点的预测值与目标值(实验值)之间应该具有最小的误差。图3分别给出了三种加载方式的仿真曲线，测试样本目标值与预测值的最大相对误差为0.048%,训练好的网络具有较强的泛化能力。

3.3 误差分析

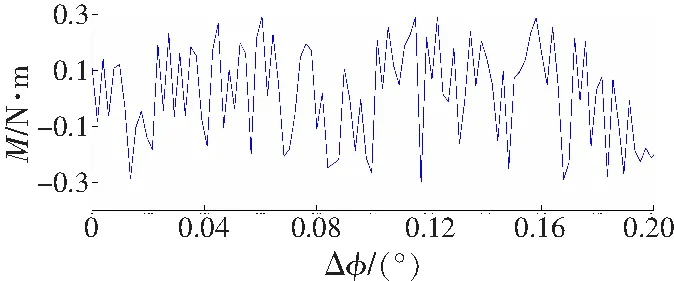
转角差曲线和误差曲线分别如图4和5所示。

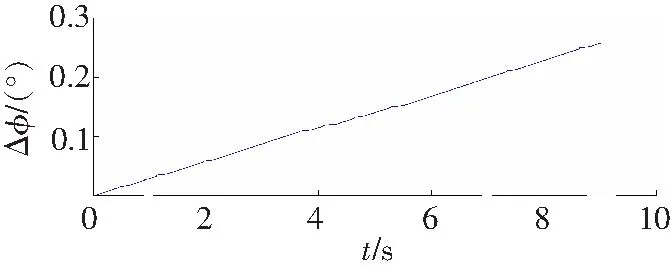
a 试件1

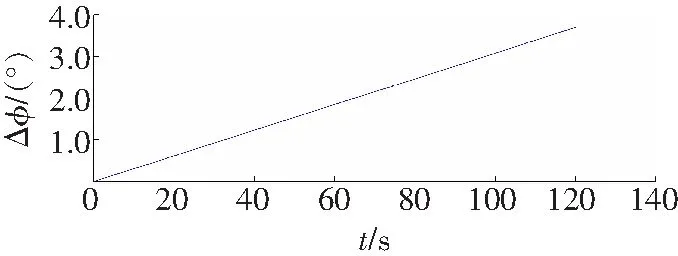
b 试件2

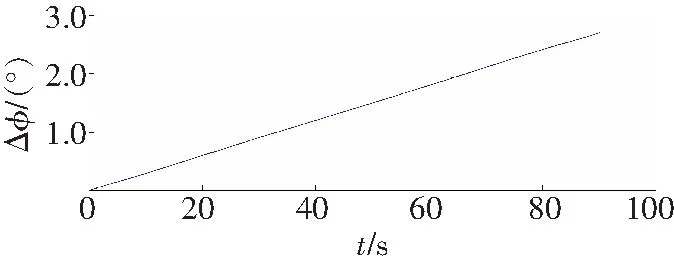
c 试件3

a 试件1

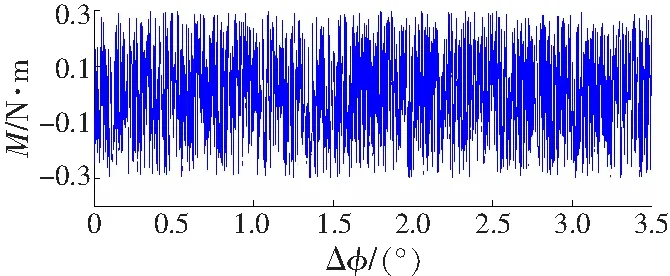
b 试件2

c 试件3

从图4实验数扰拟合曲线可以看出，测试工件的转角差在整个加载过程中，弹性阶段、屈服阶段、强化阶段表现明显，局部变形阶段表现不佳，经分析认为是加载时间过快的影响，并且扭断时间t过大，经分析认为是扭矩轴断裂后摩擦转动导致。根据该三种实验数据，由Hopfield神经网络辨识与仿真曲线比较忽略扭断时刻后试验系统影响，仿真曲线误差在1 N·m以内(图5)，仿真结果符合弹性体材料力学性能。

4 结 论

(1)Hopfield神经网络辨识可实现采煤机扭矩轴传动系统的模拟，相对于其他数学模型，具有数学建模工作量小、通用性好的特点。

(2)以采煤机扭矩轴试验台实验数据为训练样本，其结果误差在1 N·m。且仿真结果更符合材料力学理论，可实现预期目标。

(3)实验数据拟合曲线与仿真曲线比较结果表明：基于Hopfield神经网络辨识算法的采煤机扭矩轴传动系统模型，仿真精度较高，可用于工程实际应用。

[1] 刘春生.滚筒式采煤机理论设计基础[M].徐州：中国矿业大学出版社，2003.

[2] 刘春生，靳立红，闫晓林.采煤机弹性扭矩轴功能设计[J].矿业机械，2009,37(9)： 1-3.

[3] 吴卫东，郭昌利，李华亮.采煤机摇臂转矩轴的有限元分析[J].机械传动，2012,36(4)： 84-86.

[4] 刘春生，鲁士铂，张艳军，等.冲击载荷下不同有效长度扭矩轴的扭转特性[J].黑龙江科技大学学报，2014,24(3)： 253-255.

[5] 毛永骥，徐 建.神经网络控制[M].北京： 机械工业出版社，1999.

[6] 单耀祖.材料力学[M].北京： 高等教育出版社，2004.

[7] 机械工程材料性能数据手册编委会.机械工程材料性能数据手册[M].北京： 机械工业出版社，1995.

[8] 周海峰,李玉标,杨瑞锋.采煤机扭矩轴加载试验研究[J].价值工程,2014(05): 27-28.

[9] 武文虎,杨兆建,范秋霞.采煤机摇臂扭矩轴设计[J].煤矿机械,2012(11): 12-13.

[10] 冯文宾.薄煤层采煤机行走机构扭矩轴的强度分析[J].科技创新导报,2012(09): 80.

[11] 范 超.采煤机扭矩轴的疲劳分析及寿命预测[D].阜新： 辽宁工程技术大学,2012.

(编校 王 冬)

Neural network algorithm identification of twisting parameters of shearer torque axis

WanFeng1，CaiGuiying2

(1.School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China;2.School of Computer & Information Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China)

This paper seeks to overcome the unstable performance of shaft torque of the coal winning machines operating in the actual working conditions and presents an identification algorithm based on Hopfield neural network to optimize the torque shaft parameters.The study using this algorithm involves fitting the experimental data of coal winning machine torque shaft; identifying coal winning machine shaft torque parameters using the data as sample; and comparing and analyzing errors occurring between the experiment and simulation by applying MATLAB software.The results show that the algorithm promises a practical engineering application thanks to its advantages,such as a smaller modeling workload in coal winning machine torque shaft driving system,a better versatility,and simulation error of less than 1 N·m.

shearer；torque axis；Hopfield neural network；stiffness；system identification

2017-02-23

万 丰(1965-)，男，江西省南昌人，高级工程师，研究方向：测控技术、煤矿机电设备检测与控制，E-mail:1798120076@qq.com。

10.3969/j.issn.2095-7262.2017.02.005

TD421.6

2095-7262(2017)02-0118-05

A