碟盘刀齿冲击与切削复合破碎煤岩的载荷特性

刘春生，徐玉芸，李德根，袁 昊

(1.黑龙江科技大学，哈尔滨 150022；2.黑龙江科技大学 机械工程学院，哈尔滨 150022；3.黑龙江科技大学 学术理论研究部，哈尔滨 150022)

碟盘刀齿冲击与切削复合破碎煤岩的载荷特性

刘春生1，徐玉芸2，李德根3，袁 昊2

(1.黑龙江科技大学，哈尔滨 150022；2.黑龙江科技大学 机械工程学院，哈尔滨 150022；3.黑龙江科技大学 学术理论研究部，哈尔滨 150022)

为获得碟盘刀齿在不同冲击幅值下冲击与切削复合破碎煤岩的载荷特性与煤岩破碎效果，以Drucker-Prager为煤岩的本构模型，采用ABAQUS有限元软件模拟分析碟盘刀齿在冲击、切削以及冲击与切削复合作用下的载荷特性。结果表明：碟盘刀齿在冲击切削复合状态下的切削载荷比单作用切削时的载荷小20%～30%，切削载荷与冲击载荷呈反相关。其切削载荷最大值和均值随冲击幅值的增加而减小，冲击载荷反之。切削载荷均值的减小梯度大于冲击载荷均值增大的梯度。复合状态下刀齿的切削载荷幅值主要集中在低频段，低频段的幅值随冲击幅值的增加而减小。该研究为碟盘刀齿载荷特性的深入研究提供了参考。

煤岩；碟盘刀齿；冲击；切削

0 引 言

机械破碎煤岩方法在矿山开采有广泛的应用。提高破碎煤岩机械刀具的性能，对矿山的开采具有重要的意义[1]。目前，国内外学者对破碎煤岩进行了诸多研究，取得了多项的研究成果。J.T.Hagan[2]发现冲击破碎煤岩产生的径向裂纹比静压破碎煤岩长，产生的破碎范围更大。 张晓东等[3]研究了切削参数与切削效果的关系。切削速度与正压力、转速成正比，与接触面积成反比。Evans[4]提出最大拉应力理论，认为煤岩破碎是由刀具切入煤岩时的拉应力造成的，引起材料脆性断裂破坏的因素是最大拉应力。Nishimatsu[5]提出煤岩破碎面遵循库伦-摩尔准则。牛东民[6]提出的断裂力学破煤理论，认为煤岩在刀具的作用下，沿着煤岩体本身的层理和节理破碎。Wang等[7]采用有限元模型模拟了穿透岩石碎屑的形成过程。Han等[8]根据Mohr-Coulomb模型，建立了多冲击下的数值模型。Muro等[9]利用振动截齿对煤岩进行了截割实验研究，指出采用正弦波形式振动截割比三角形式有效。徐小荷等[10]指出刀具侵入岩石的破碎煤岩过程有跃进式侵入、承压核和破碎角稳定等规律。陈才贤等[11]应用混沌理论探讨动静载荷对刀具在切削破碎煤岩的影响，表明破碎硬岩时，在破裂深度与破碎体积方面，动载荷切削与静压切削相比，具有明显优势。杨金强等[12]利用ANSYS/LS-DYNA软件对盘形滚刀回转切割煤岩进行数值模拟，分析了单把滚刀的受力情况以及跃进式破碎的特点。目前，国内外学者对冲击与切削复合破碎的研究成果不多。笔者采用ABAQUS软件模拟碟盘刀齿在冲击与切削复合作用下破碎煤岩研究其载荷特性。

1 刀齿破碎煤岩的本构模型与破坏准则

碟盘刀齿破碎煤岩有两个方向的运动：一是垂直于刀盘轴线方向的径向切削运动；二是沿碟盘刀齿轴线方向的轴向冲击运动。均布在圆周方向的刀齿通过轴向冲击预损伤煤岩及其切削作用联合破碎煤岩。

基于等效塑性应变和耗散能的煤岩破坏准则，采用扩展的线性德鲁克-普拉(Drucker-Prager)塑性本构模型[13]，模拟碟盘刀齿破碎煤岩的过程，其中，线性Drucker-Prager模型的屈服面的关系函数为

F=σ-σetanφ-d=0，

(1)

(2)

式中：σ——偏应力参数，MPa；

σe——等效应力，MPa；

φ——屈服面上的斜率，通常指内摩擦角，(°)；

d——粘聚力，MPa；

K——三轴拉压实验的屈服应力比；

q——米斯等效应力，MPa；

r——第三偏应力不变量，MPa。

当K=1时，屈服面为Mises屈服面的圆形。为保证屈服面是凸面，要求0.778≤K≤1.0，其中，K可以由内摩擦角进行标定，

(3)

粘结力和摩擦力构成了煤岩的强度，强度准则为

|τ|=d+tanφ，

(4)

式中：τ——切应力，MPa。

2 冲击与切削破碎煤岩的数值模拟

2.1 切削破碎煤岩

碟盘刀齿破碎煤岩受刀齿与煤岩接触间隙的影响，碟盘刀齿破碎煤岩载荷的衰减影响不能忽略。在数值模拟碟盘刀齿破碎煤岩时作如下假设：碟盘刀齿的材料为各向同性；刀盘为不可变形刚体；煤岩为长方体、各向同性材料，忽略煤岩中原始裂纹、构造应力和煤岩内部空隙压力。

2.1.1 模型的建立

采用ABAQUS有限元分析软件模拟碟盘刀齿冲击与切削破碎煤岩，在Pro/E软件中绘制碟盘刀齿和煤岩的三维模型，将其导入到ABAQUS的Part模块。由于主要研究碟盘刀齿在不同冲击幅值下破碎煤岩的载荷特性，仅模拟碟盘刀齿的单个齿，煤岩的参数[14]见表1。

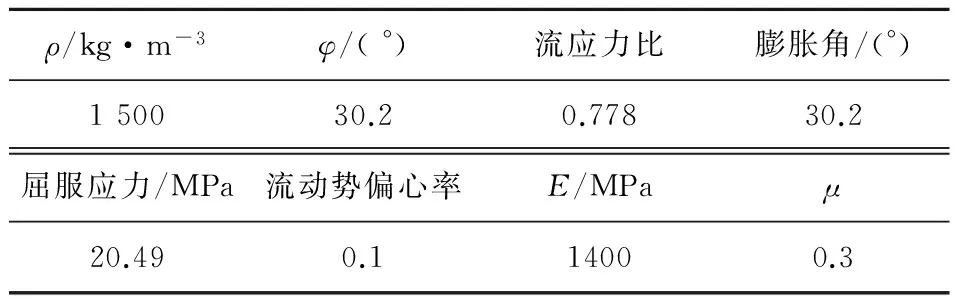
表1 煤岩参数Table 1 Rock parameter

在刀齿上设立参考点，绑定到参考点上，接触类型为面到面的接触，将接触面和上表面设置为自由面，其他面固定，刀齿采用四面体C3D4单元类型，煤岩采用六面体C3D8R单元类型。

2.1.2 模拟结果

模拟参数选取切削深度14 mm，速度500 mm/s，时间0.04 s。单作用切削时的切削载荷的变化曲线和应力云图，如图1所示，图中，Fd为切削载荷，Fdm为切削载荷上峰值包络线，Fdv为均值。图1a显示切削载荷随着位移的增加波动增加，在0.025 s时切削载荷达到最大值，迅速减小之后切削载荷继续波动增加。碟盘刀齿在单作用切削破岩时，随着切削载荷的增加发生小煤块崩落，切削载荷波动增大。大煤块崩落时，切削载荷达到最大值后减小再增大，完成一个破碎周期，开始下一个破岩周期。

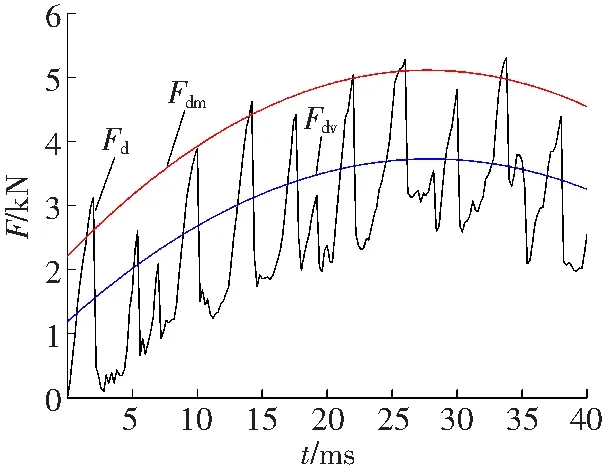
a 切削载荷

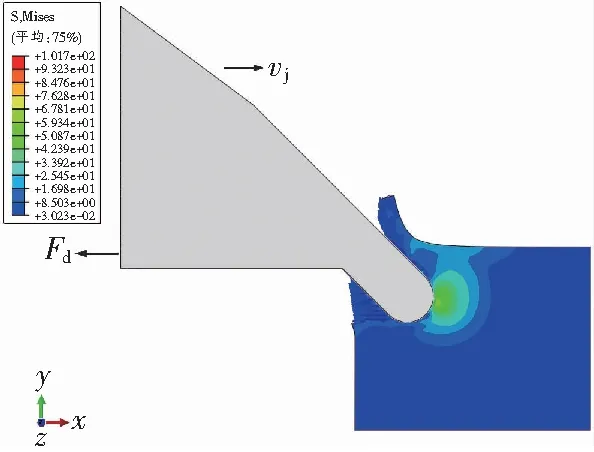
b 应力云图

2.2 冲击破碎煤岩

碟盘刀齿轴向冲击破碎煤岩时，在轴向的位移为正弦函数：

x(t)=-Asinωt，

(5)

式中：A——振动冲击幅值，mm；

ω——振动冲击角频率，rad/s,ω=2πf;

f——振动冲击频率，Hz ；

t——时间，s。

2.2.1 模型的建立

将碟盘刀齿与煤岩的三维模型导入ABAQUS中，在Assembly中定义碟盘刀齿与煤岩的相对位置，在Mesh模块中划分网格，其中，单作用冲击破碎煤岩轴向冲击速度为vi。

2.2.2 模拟结果

碟盘刀齿冲击破碎煤岩时，冲击幅值为0.5～2.5 mm、间隔为0.5 mm。其中，冲击幅值为1.0和2.5 mm的冲击载荷与应力云图，如图2所示，图中，Fdc为冲击载荷，x(t)为位移曲线。

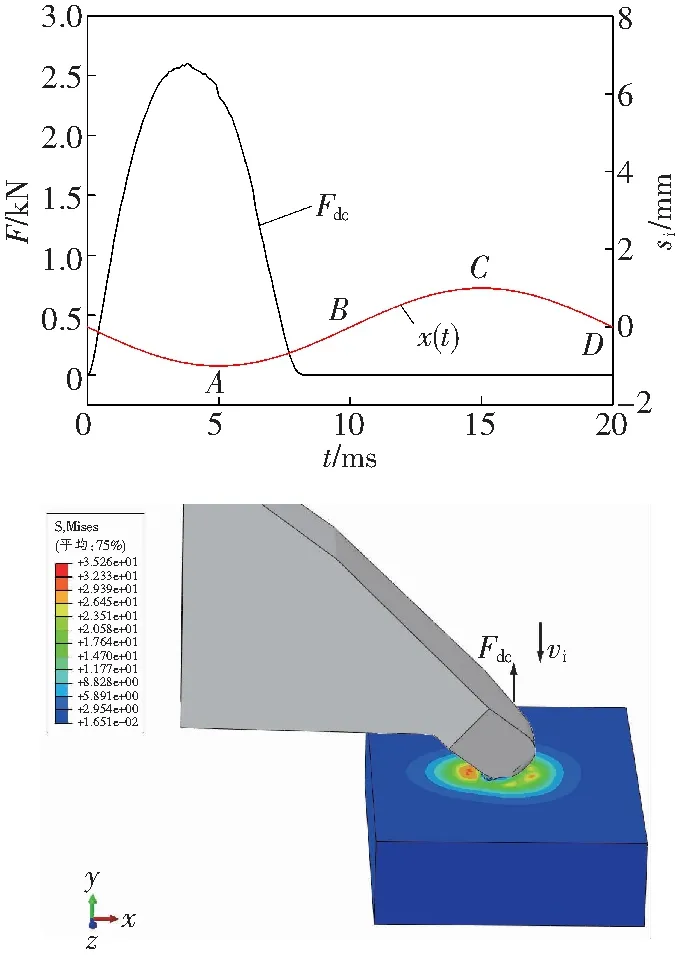
a A=1.0 mm

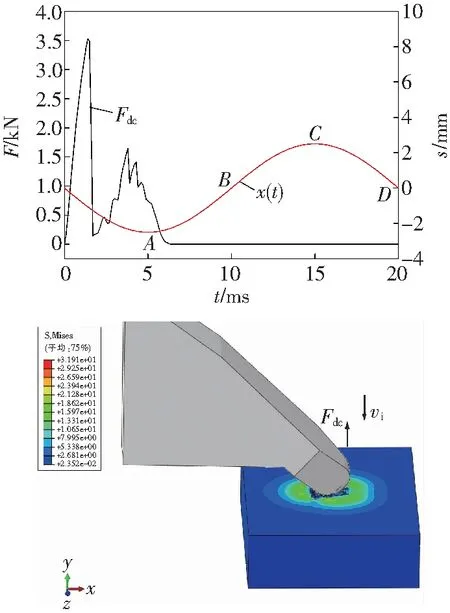
b A=2.5 mm

由图2a可见，在碟盘刀齿与煤岩接触之前，碟盘刀齿所受载荷为0；当碟盘刀齿的位移在OA段时，其所受的载荷逐渐增大，最大值为2.5 kN；当碟盘刀齿的位移在AB段时，碟盘刀齿的载荷逐渐减小，最小值为0。此时碟盘刀齿已离开了煤岩；当刀齿位移在BD段时刀齿载荷为0。由此可知，当冲击幅值为1.0 mm时，碟盘刀齿的载荷随冲击位移的变化而变化，并具有一定的周期性。由于煤岩受到碟盘刀齿的冲击作用发生塑性损伤，致使载荷曲线具有一定的延时。由图4b可见，冲击幅值为2.5 mm时与冲击幅值为1.0 mm时的载荷具有类似的规律，同时，在冲击的上半周期OB段时，出现两个较大的锯齿状载荷波动，即在一个冲击周期内碟盘刀齿所受的载荷先直线增大至3.5 kN后迅速减小接近0，之后载荷又缓慢增大呈锯齿状波动，直至最后趋近于0。由此，可以看出冲击幅值对煤岩的损伤有较大的影响。

3 冲击与切削复合破碎煤岩的数值模拟

3.1 模拟参数

在不改变煤岩参数和碟盘刀齿形状的前提下，对比分析单一作用切削和单一作用冲击与冲击切削复合作用时的载荷谱。碟盘刀齿在冲击与切削复合作用时，改变碟盘刀齿的冲击幅值，研究冲击与切削载荷的变化形式，数值模拟参数见表2。刀齿冲击与切削复合破碎煤岩的有限元模型，如图3所示。碟盘刀齿存在径向切削运动和轴向冲击运动，其速度分别为vj和vi。

表2 模拟参数Table 2 Simulation parameters

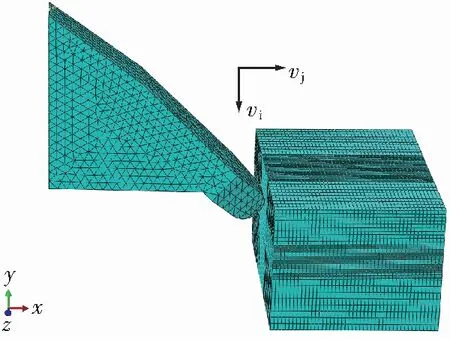
图3 单齿复合破碎煤岩模型Fig.3 Model for single tooth broken rock

3.2 模拟结果

3.2.1 切削载荷

冲击幅值为0.5～2.5 mm、间隔为0.5 mm时进行刀齿冲击切削复合破碎煤岩的数值模拟，其中A为1.0和2.5 mm时切削载荷的变化曲线与应力云图，如图4所示。

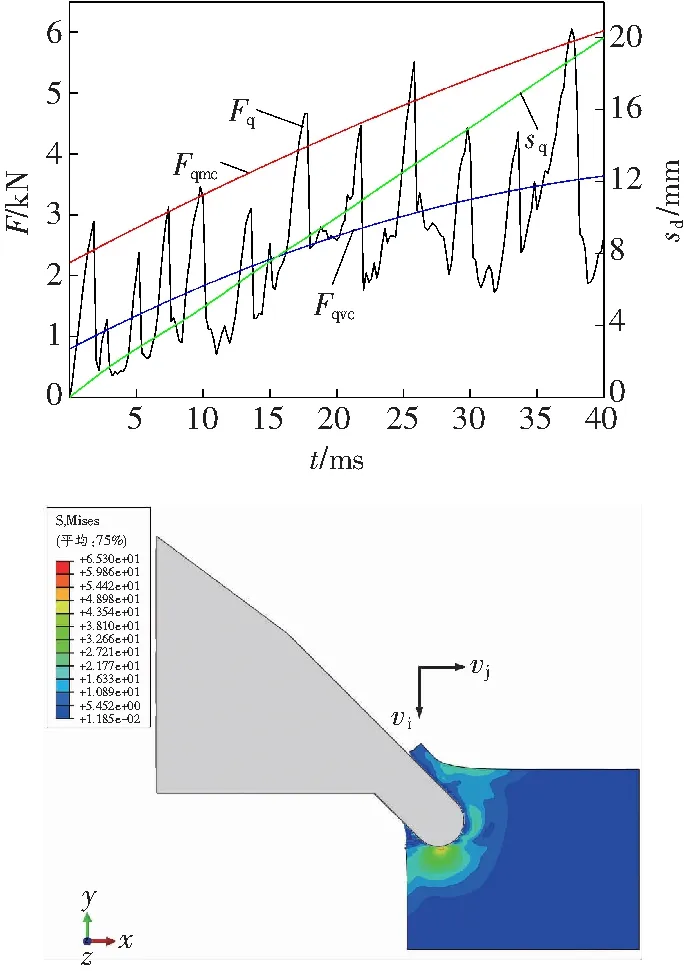
a A=1.0 mm

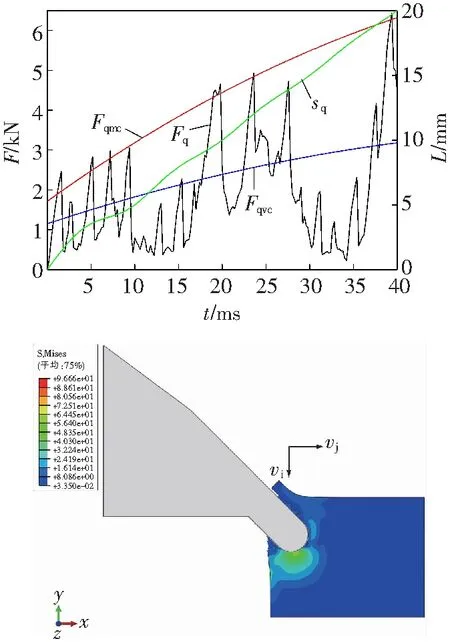
b A=2.5 mm

图4中，Fq为切削载荷，Fqmc为切削载荷上峰值包络线，Fqvc为切削载荷均值包络线。刀齿的复合位移

(6)

式中：si——刀齿轴向冲击位移，mm；

sj——刀齿径向切削位移，mm。

由式(6)可知，刀齿的运动具有波动较大的曲线。由图4a可见，刀齿的切削载荷随复合位移的增大，呈锯齿状波动，载荷有上升趋势，当复合位移为0时，刀齿的切削载荷为0，随着复合位移的增大，载荷呈锯齿状波动，每个锯齿波形的峰值有增大趋势。由图4b可见，刀齿的切削载荷的变化规律与冲击幅值为1.0 mm的类似，但随复合位移的增大，与图4a相比载荷锯齿峰值的波动较大，其峰值整体有减小趋势。由此可见，刀齿的切削载荷随着位移的增大呈增大趋势，同时冲击幅值对其载荷的波动影响较大。随着冲击幅值的增大，载荷上峰值有减小趋势。

3.2.2 冲击载荷

冲击幅值为0.5～2.5 mm、间隔为0.5 mm时进行刀齿冲击切削复合破碎煤岩的数值模拟。其中A为1.0 mm和2.5 mm时冲击载荷的变化曲线与应力云图，如图5所示，图中，Fc为冲击载荷，vi为轴向速度

vi=-Aωcosωt,

(7)

轴向速度vi和径向速度vj的合成速度为

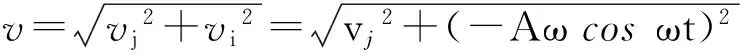
(8)

刀齿合成速度的方向为

1) 开展磁通切换发电动机的研究。对三种电动机开展综合全面的研究，并通过实际测试及计算，研究其特性，发挥其实际作用。

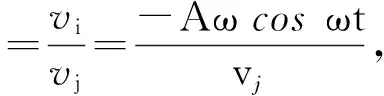
(9)

式中：φ——轴向速度vi和径向速度vj的角度。

由图5a可以看出，刀齿的冲击载荷随着轴向速度呈周期锯齿性波动。当轴向速度达到正向峰值时a点时，冲击载荷达到载荷曲线的峰谷；当轴向速度曲线达到峰谷b点时，冲击载荷曲线达到波峰。由式(9)可知，当冲击幅值为0.5 mm时，合成速度的方向角φ在-17°～17°之间变化。

由图5b可以看出，刀齿的冲击载荷随着轴向速度呈周期锯齿性波动。与图5a相比，刀齿的冲击载荷锯齿峰值有增大趋势。当冲击幅值为2.5 mm时，合成速度方向角φ在-57.5°～57.5°之间变化，随冲击幅值的增大速度方向的变化区间随之增大。由此可见，碟盘刀齿在冲击与切削复合作用下的冲击载荷的最大值随冲击幅值的增大而增大，则破碎煤岩时的能耗也随冲击幅值的增加而增加；冲击载荷的变化规律与复合速度的幅值和方向变化规律有着一致性。

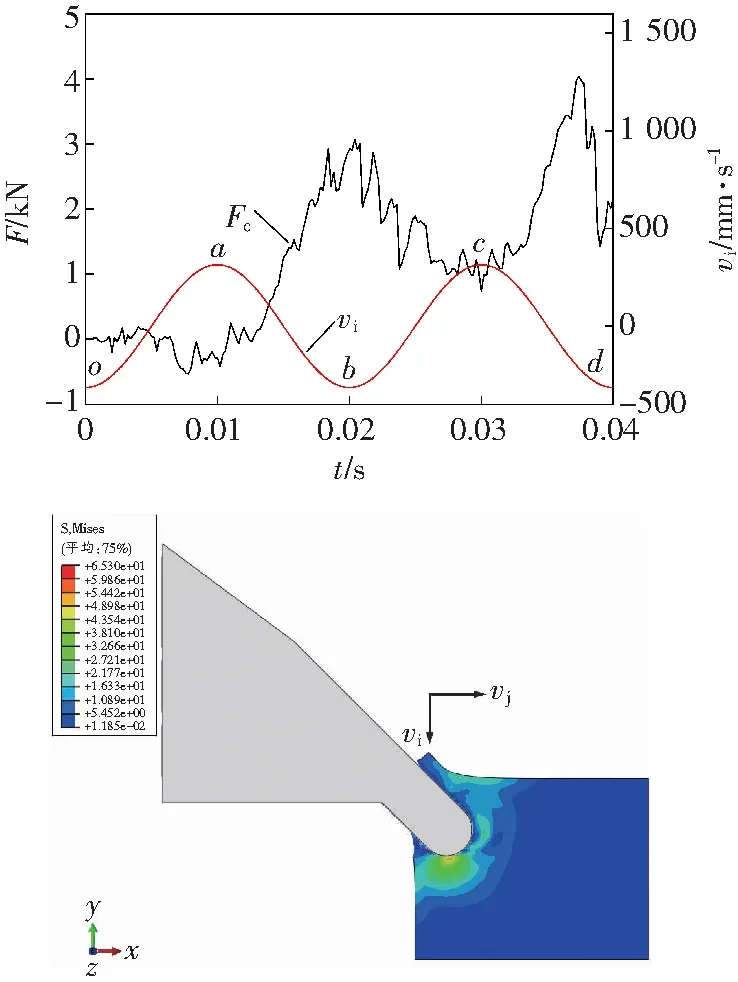
a A=1.0 mm

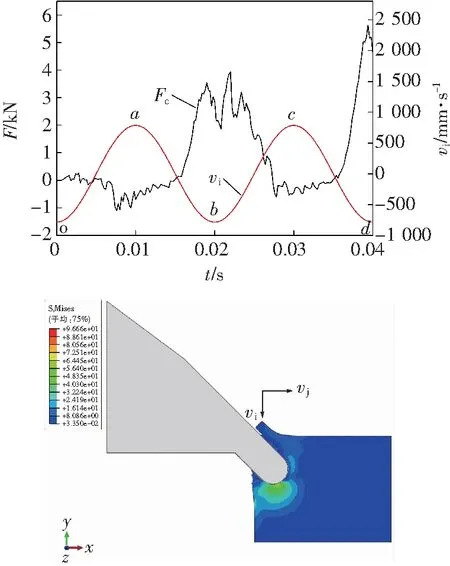
b A=2.5 mm

碟盘刀齿与煤岩的相互作用关系，如图6所示。其中，实线表示刀齿与煤岩接触，虚线表示刀齿破碎煤岩。其数学表述为

h=vjttanθ，

(10)

Δh=vjttanθ-Asinωt,

(11)

式中：θ——碟盘刀齿前端斜面与碟盘刀齿底面之间的夹角，(°)；

h——径向切削时，轴向位移的分量，mm；

由于碟盘刀齿前端斜面作用，刀齿在径向切削煤岩时，在轴向上同样对煤岩形成剪切破碎煤岩作用，其轴向位移h可由式(10)确定，轴向冲击位移之差Δh可由式(11)确定。由图5a和图6可见，刀齿开始接触煤岩时，其受到煤岩的反作用力，当刀齿径向切削在轴向上的位移大于在轴向的位移时，即Δh>0时，冲击载荷为负值，此时煤岩受压，随着冲击位移的继续增大，冲击载荷由负值变为正值，并且同时有增大趋势。由图5b和图6可见，当冲击幅值为2.5 mm时，其冲击载荷变化规律与冲击幅值为1.0 mm的变化规律具有一致性，但随着冲击幅值的增大刀齿的冲击载荷负值也增大。

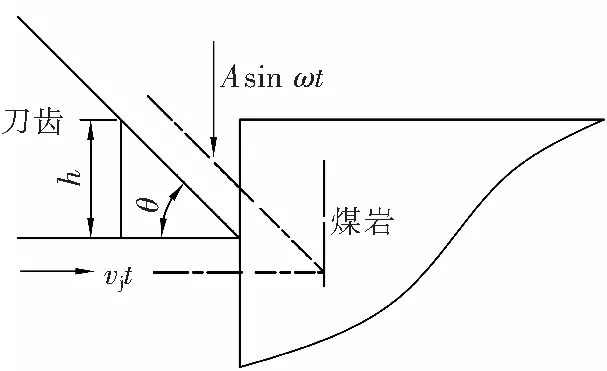
图6 碟盘刀齿与煤岩初接触时受力模型Fig.6 Disc cutter tooth and coal rock contact force model

4 数值模拟结果分析

4.1 统计特征

为研究冲击幅值对冲击与切削载荷的影响及相互关系，对单一作用切削和冲击与冲击切削复合作用时的载荷曲线进行分析。由于碟盘刀齿在冲击与切削复合状态下的冲击载荷曲线在开始和最后阶段受到刀齿未与煤岩完全接触以及载荷曲线周期少的影响，因此，取冲击载荷曲线中间的一个完整的运动周期进行分析，积分求得其平均值，定义其为冲击载荷的均值Fcv，将冲击载荷第一个峰值的数值定义为冲击载荷的最大值Fcm。复合切削载荷曲线的最大值包络线平均值定义为载荷的最大值Fqm，复合切削载荷均值Fqv，单一作用冲击破碎煤岩和单一作用切削时的分析方法同冲击与切削复合破碎煤岩时分析方法一致。刀齿在冲击切削复合作用下的载荷统计结果见表3。刀齿在单一作用冲击破碎煤岩时的冲击载荷最大值为2.221 kN，单一作用切削时的切削载荷最大值为5.308 kN、均值为2.633 kN。

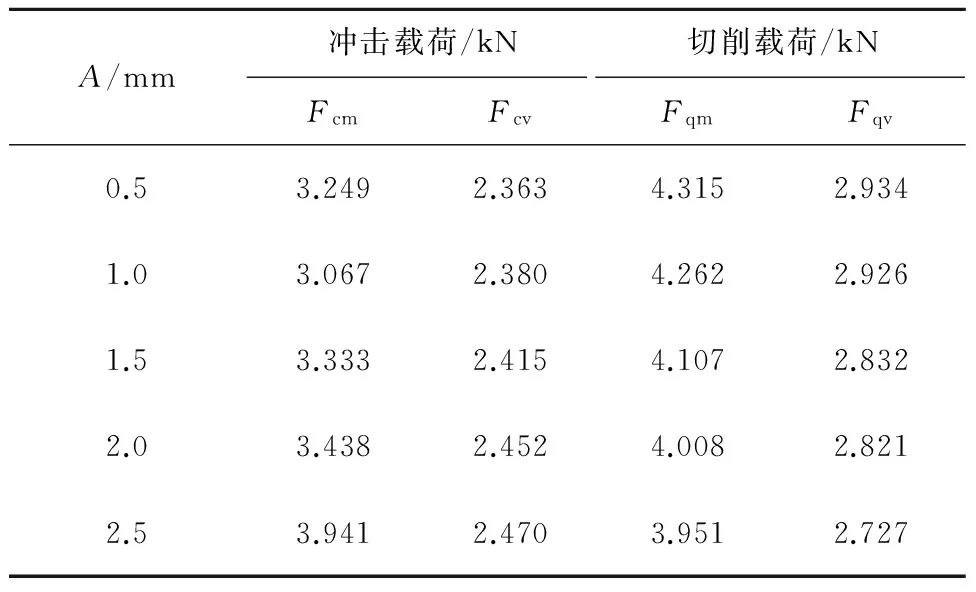
表3 不同冲击幅值变化下冲击与切削载荷Table 3 Changes under impact and cutter of different amplitude

由表3可以看出，在复合作用下，碟盘刀齿所受的冲击载荷较大，在五种不同的冲击幅值作用下冲击载荷的最大值在3.067～3.941 kN之间，冲击载荷的均值在2.363～2.470 kN之间；在复合作用下，在不同冲击幅值作用下切削载荷最大值在3.901～4.315 kN之间，切削载荷的均值在2.727～2.934 kN之间。刀齿在冲击与切削复合作用与单一作用时的冲击载荷与切削载荷变化规律，如图7所示。图中，Fdq为单一作用切削载荷最大值，Fdc为单作用冲击载荷最大值，Fcm为复合冲击载荷最大值，Fcv为复合冲击载荷均值。

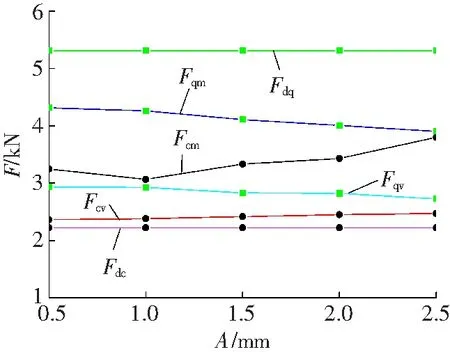
图7 载荷曲线Fig.7 Load curve

由图7可见，刀齿在冲击与切削复合作用下，切削载荷的最大值Fqm与均值均Fqv比冲击载荷最大值Fcm和均值Fcv大。复合状态下的切削载荷比单一作用时的切削载荷Fdq小20%～30%，单一作用时的冲击载荷Fdc最小。当冲击幅值从0.5 mm增加至2.5 mm时，冲击切削复合作用下的切削载荷的最大值与均值分别减小10%和7%。由此可以看出，切削载荷随冲击幅值增大而减小，减小不是很显著。从图4可看出，载荷曲线下围成的面积与冲击幅值增大而明显减小。其面积与能耗有着正比的关系，说明冲击幅值增大切削能耗明显减小。冲击载荷曲线第一个峰值最大值与均值分别增加21%和4.1%。

4.2 频率特征

对刀齿冲击与切削复合破碎煤岩的切削载荷谱进行FFT变换，其频谱图如图8所示。

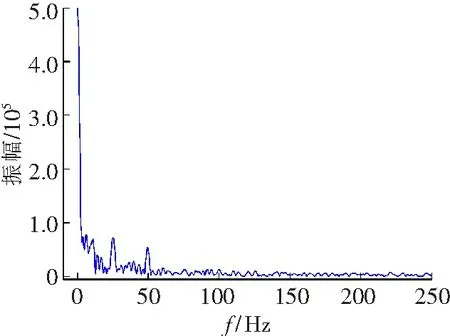
a A=1.0 mm

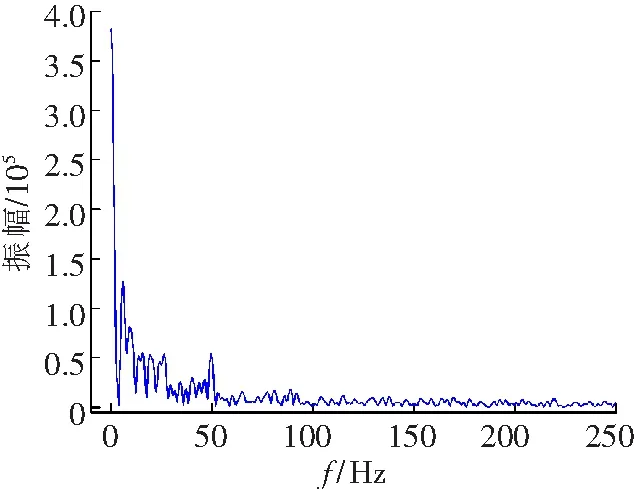
b A=2.5 mm

切削载荷幅值主要集中在0～60 Hz的低频区域,五组切削载荷谱极为相似。由图8可见，当冲击幅值为1.0和2.5 mm时，在低频区域,载荷信号的幅值较大，且在频率为50 Hz处载荷信号的幅值出现峰值，并且随着刀齿冲击幅值的增加冲击载荷在低频区域的幅值随之减小，频率为0 Hz的直流分量部分是切削载荷频谱图的主要成分，而在高频区域幅的变化区间主要在0～5.5×103。

5 结 论

(1)冲击切削复合状态下最大切削载荷比单一作用切削时的载荷小20%～30%，并且碟盘刀齿在复合作用时切削载荷的最大值与均值两方面均存在随着冲击幅值的增大而减小的趋。由此说明，冲击切削复合作用的效果较单一作用切削时具有一定优势。

(2)碟盘刀齿在冲击切削复合作用时切削载荷和冲击载荷较大，在冲击幅值为0.5～2.5 mm时冲击载荷曲线第一个峰值的最大值可出现在3.067～3.841 kN，切削载荷最大值在3.901～4.315 kN。冲击载荷的均值在2.363～2.470 kN，切削载荷的均值在2.727～2.934 kN。随冲击幅值的增加冲击载荷最大值与均值分别增加21%和4.1%，切削载荷最大值与均值分别减小10%和7%，载荷曲线下围成的面积明显增减小。由是，切削载荷均值的减小梯度大于冲击载荷均值增大的梯度。

(3)碟盘刀齿的切削载荷幅值主要集中在低频区域，且随冲击幅值的增大切削载荷在低频区域的幅值随之减小，直流分量0 Hz是切削载荷幅值的主要成分，高频区域幅值的变化区间主要集中在0～5.5 kN。

[1] 刘春生,于信伟,任昌玉.滚筒式采煤机工作机构[M].哈尔滨： 哈尔滨工程大学出版社，2010.

[2] HAGAN J T.Shear deformation under pyramidal indentation in soda-lime glass[J].J Mater Sci,1980(5): 1417-1424.

[3] 张晓东，易发全，张 强，等.PDC 钻头与煤岩相互作用规律试验研究[J].江汉石油学院学报，2003，25(S): 64-65.

[4] Evans I.A theory of the cutting force for point-attack picks[J].International Journal of Rock Mechanics and Mining Science,1984,2(1): 64-71.

[5] Nishimatsu Y.The mechanics of rock cutting [J].International Journal of Rock Mechanics and Mining Science,1972,9(3): 261-270.

[6] 牛东民.刀具切削破碎煤岩机理研究[J].煤炭学报，1993,18(5): 49-52.

[7] Wang J K，Lehnhoff T F.An experimental and theoretical investigation[J].Rock mechanics,1976,3(1): 185-207.

[8] Han G,Bruno M,Grant T.Dynamically modeling rock failure in percussion drilling[C]//Proceedings of the 40th rock mechanics symposium,Beijing: s.n.2005: 805-819.

[9] Muro T,Takegaki Y,Yoshikawa K.Impact cutting property of rock material using a point attack bit[J].Journal of Terramechanics,1997,34(2): 83-108.

[10] 徐小荷，于 静.岩石破碎学[M].北京： 煤炭工业出版社，1984.

[11] 陈才贤，赵伏军，杨军伟.冲击切削破碎煤岩的混沌动力学特性[J].采矿技术,2011(3): 1671-2900.

[12] 杨金强.盘形滚刀受力分析及切割煤岩数值模拟研究[D].北京: 华北电力大学，2007.

[13] 费 康，张建伟.ABAQUS在岩土工程中的应用[M].北京： 中国水利水电出版社，2010.

[14] 刘春生,王庆华,任春平.镐型截齿载荷谱定量特征的旋转截割实验与数值模拟[J].黑龙江科技大学学报,2014,24(2): 195-199.

(编辑 晁晓筠 校对 王 冬)

Load characteristics behind disc cutter teeth impacting and cutting composite broken coal rocks

LiuChunsheng1,XuYuyun2,LiDegen3，YuanHao2

(1.Heilongjiang University of Science & Technology，Harbin 150022,China；2.School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China;3.Department of Academic Research,Heilongjiang University of Science & Technology，Harbin 150022，China)

This paper is motivated by the need for investigating the load characteristics behind the disc cutter teeth used to impact and cut composite broken coal rocks,and the crushing effect on coal rocks.The study drawing on Drucker-Prager as the constitutive model of coal rock and using ABAQUS finite element software works on simulating the load characteristics behind the disc cutter teeth exposed to impact and cutting,and the combined action of impact and cutting; and comparing and analyzing the statistical and frequency characteristics of the impact and cutting load spectrum in the single impact and single action cutting load spectrum and the impact cutting compound state.The work demonstrates that given the compound state of impact cutting,disc cutter teeth are subjected to a 20%～30% smaller cutting load than when a single action cutting process is at work; disc cutter teeth exposed to the combined action have a maximum and mean cutting load tending to decrease with an increased impact amplitude,but the case is different with impact load; the cutting load shows a greater reduction gradient in mean value than the increased gradient of the impact load mean value; the teeth under the composite state shows the cutting load amplitude which is concentrated mainly in low frequency and tends to decrease with an increase in impact amplitude; and a positive correlation exists between cutting load and impact load.The research may provide a reference for a deeper insight into the load characteristics of disc cutters.

coal rocks; cutting-wedge cutter tooth; impact; cutting

2017-01-16

国家自然科学基金项目(51674106;51274091)

刘春生(1961-)，男，山东省牟平人，教授，研究方向：机械设计和液压传动与控制，E-mail:liu_chunsheng@163.com。

10.3969/j.issn.2095-7262.2017.02.001

TD421.61

2095-7262(2017)02-0097-07

A