串联机械臂的RBF自适应滑模控制

闵振辉，陈焕林

(黑龙江科技大学 机械工程学院,哈尔滨 150022)

串联机械臂的RBF自适应滑模控制

闵振辉，陈焕林

(黑龙江科技大学 机械工程学院,哈尔滨 150022)

针对串联机械臂在控制过程中存在的问题，以径向基神经网络和滑模变结构控制理论，建立径向基神经网络自适应滑模控制器和多关节机械臂模型。利用径向基神经网络对多关节机械臂模型的不确定性因素进行函数逼近，由李雅普诺夫定理证明了控制系统的稳定性。通过对机械臂的位置跟踪控制，检验了普通滑模变结构控制器和径向基神经网络自适应滑模控制器的控制结果。径向基神经网络自适应滑模控制器与普通滑模控制器的对比仿真表明，径向基神经网络自适应滑模控制方法能够更好地削弱抖振，控制效果优于滑模变结构控制器。

滑模变结构控制；机械手臂；径向基神经网络

0 引 言

串联多关节工业机械臂是一个多输入多输出，且具有非线性、耦合性和时变性的复杂不确定性系统[1]。传统控制方法针对串联多关节刚性机械臂这类自然不稳定系统,实际上无法取得理想的控制效果[2]。因此对具有模型误差、干扰甚至参数未知的多关节机器人控制方法的研究，具有极高的价值。

滑模变结构控制非常适用于串联机械臂这样的不确定性被控对象。其滑动模态对系统的干扰和参数摄动具有较好的适应性[3]。特别是其可以构造变结构控制，使得扰动等不能影响滑动模态，适用于线性和非线性系统、定常与时变、确定和不确定系统等。单纯的滑模变结构控制器在针对串联机械臂这样的被控对象时，虽能取得一定的效果，但并不能抑制抖振，这对机械臂的伺服系统是非常不利的。文献[4]中提出了一种新型的机械臂自适应控制方法，提高了滑模控制对未知摄动的适应性。文献[5]中将滑模变结构控制与神经网络技术相结合，提出了一种神经网络滑模自适应控制方法。文献[6]中针对被控对象模型建立不精确的问题，提出了一种机械臂的神经网络滑模控制方法，但对抖振问题没有做出相应的分析。针对串联机械臂的轨迹跟踪问题，笔者采用基于RBF神经网络的自适应滑模控制方法，自适应律由Lyapunov方法导出，利用RBF神经网络逼近机械臂模型中的不确定因素，结合滑模控制在有效地提高位置跟踪精度的同时削弱抖振。

1 串联多关节机械臂动力学模型

典型串联多关节机械臂的动力学方程可以由拉格朗日方程得到[7]：

(1)

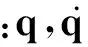
M(q)——n×n阶关节空间惯量矩阵；

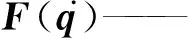
G(q)——n×1阶重力加速度矩阵；

τd——干扰或不确定因素；

τ——与广义坐标q对应的广义驱动力向量。

其跟踪误差为

e(t)=qd(t)-q(t)，

(2)

式中：qd(t)——机械臂关节角位移目标值；

q(t)——机械臂关节角位移实际值。

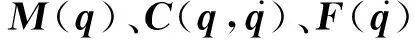
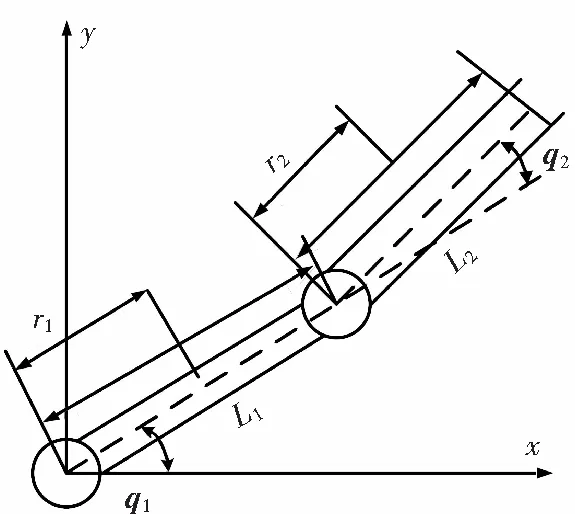
图1 两自由度机械臂模型Fig.1 Model of two degree freedom manipulator

2 RBF自适应滑模控制算法

串联多关节机械臂的精确模型建立非常困难。式(1)中存在的不确定因素使实际控制过程中采用的被控对象模型存在误差。引起误差的原因是多方面的，主要包括连杆的结构参量误差和连杆的运动变量误差引起的位置误差、控制系统误差(检测误差和指令滞后等)和随机误差等[8]。RBF网络是一种结构简单、收敛速度快、能够逼近任意非线性函数的神经网络，在模型不确定系统中得到广泛应用[9-11]。利用RBF网络逼近多关节机械臂方程中的不确定部分，能够有效提高滑模变结构控制的精度。

2.1 滑模控制器的设计

根据式(1)和式(2)设计滑模面函数为

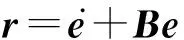
(3)

式中：B——滑模面常数，B=diag(αi),对两自由度机械臂取i=2，且αi>0；

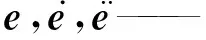
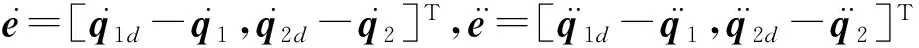
将式(3)代入式(2)可得

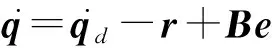
进一步可得

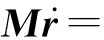
(4)

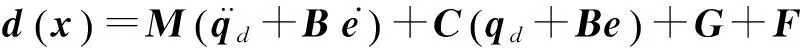
在工程实际中，由于不确定因素的存在，使得控制系统的性能受到影响，会引起传统滑模控制器比较明显的抖振[1]。对于不确定因素d(x)，利用RBF神经网络进行逼近，根据d(x)表达式，网络输入取

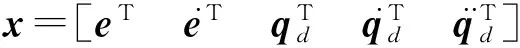
设计控制律为

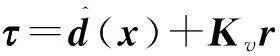
(5)

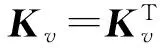
将式(5)代入式(4)，得

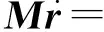
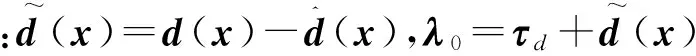
对上述控制律引入Lyapunov函数

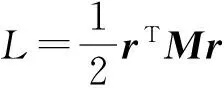
则

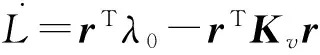
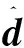
2.2 控制器自适应律的设计

2.1节叙述了串联多关节机械臂的模型中存在不确定因素。为了取得更好的效果，削弱系统抖振，利用RBF神经网络对模型的不确定因素进行自适应补偿，提高建模精度。RBF神经网络由三层组成，输入层节点传递输入信号到隐层，隐层节点由核函数构成，而输出层节点通常是简单的线性函数，如图2所示。

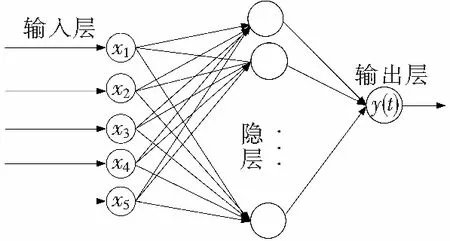
图2 RBF神经网络结构Fig.2 Structure of RBFNN

RBF神经网络的核函数式(6)选择高斯核函数：

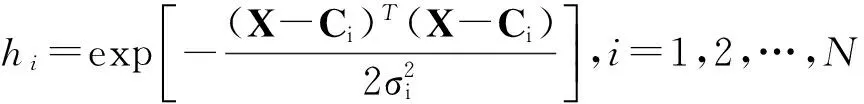
(6)

式中：hi——第i个隐层节点的输出；

X——输入样本，X=(x1,x2,…,xn)；

Ci——高斯函数的中心值；

σi——标准化常数；

N——隐层节点数。

y=Wh(x)，

式中：W——隐层到输出层的连接权值矩阵；

y——神经网络的输出。

由RBF网络逼近d(x)，则RBF神经网络的输出为

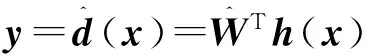
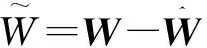
可得

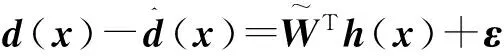
式中：ε——RBF网络逼近误差。

利用RBF神经网络逼近串联多关节机械臂模型的不确定因素d(x)后，控制律变化为

(7)

式中：υ——用于克服神经网络逼近误差ε和干扰τd的鲁棒项。

将式(7)代入式(4)，得

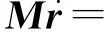
(8)

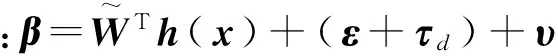
‖τd‖≤ρN；

‖ε‖——ε的界，εN为很小的正数；

‖τd‖——τd的界，ρN为很小的正数。

式(7)中鲁棒项的设计直接影响RBF神经网络逼近误差及对干扰的克服。结合ε和τd，鲁棒项υ设计为

υ=-(εN+βN)sgn(r)，

由式(7)的控制律，设计神经网络的自适应律为

通过RBF网络自适应环节的引入，滑模控制器可以通过RBF网络的学习能力根据模型的误差和干扰不断调整控制器的输出，从而改善普通滑模控制器存在的抖振问题。

2.3 稳定性分析

由2.2节设计的控制律和自适应律定义Lyapunov函数

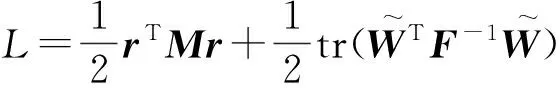
可知

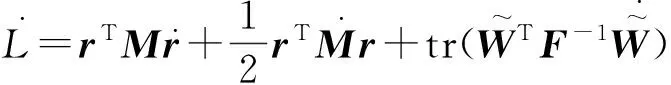
(9)

式中：tr——矩阵求迹运算符。

将式(8)代入(9)，得

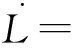
则

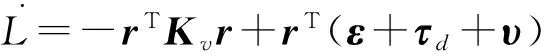
由于

rT(ε+τd+υ)=rT(ε+τd)+rTυ=rT(ε+τd)- ‖r‖(εN+ρN)≤0，

故

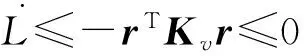
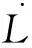
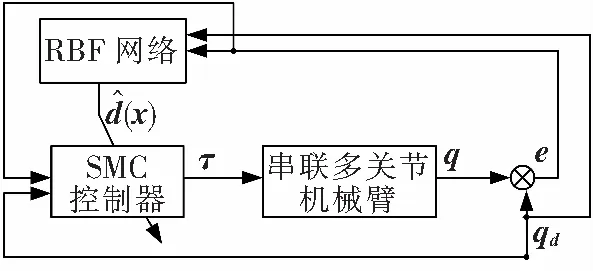
图3 RBF自适应滑模控制系统结构Fig.3 Structure of RBFNN adaptive sliding system

3 仿真研究

为了验证RBF神经网络自适应滑模控制算法，取图1所示二关节串联机械手为研究对象，其物理参数数值为：L1=L2=0.4 m；m1=m2=0.5 kg；r1=r2=0.2 m。

可知式(1)中的各系数阵为

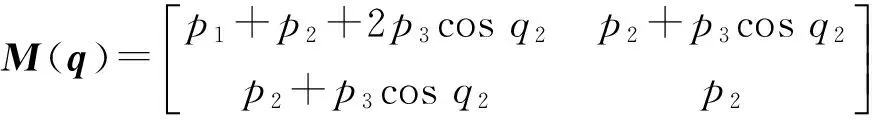
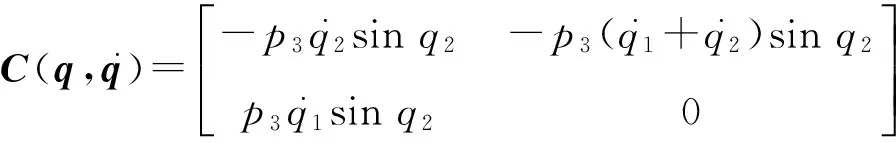
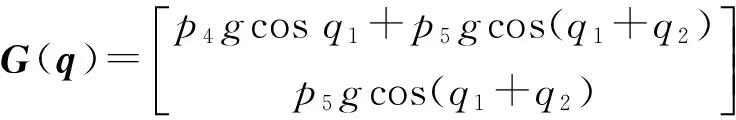
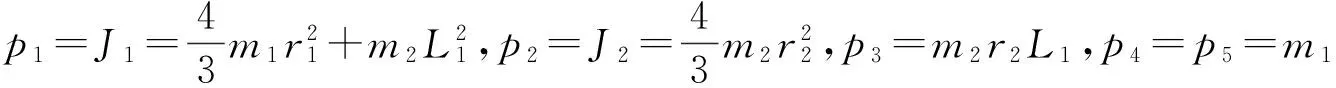
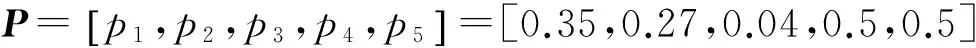
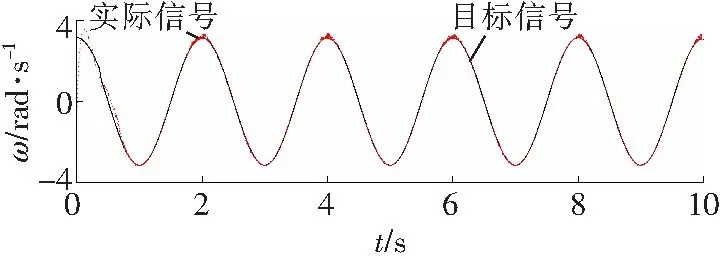
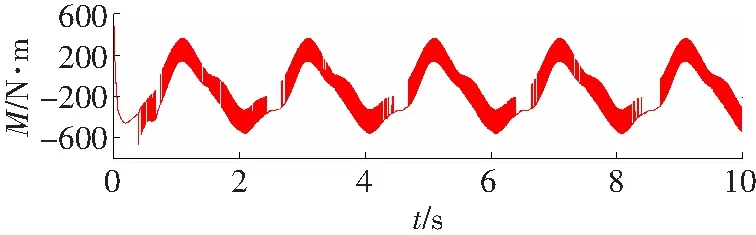
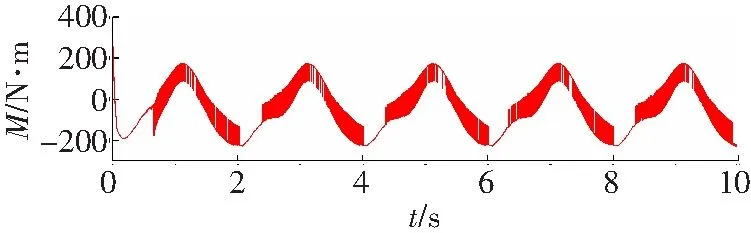
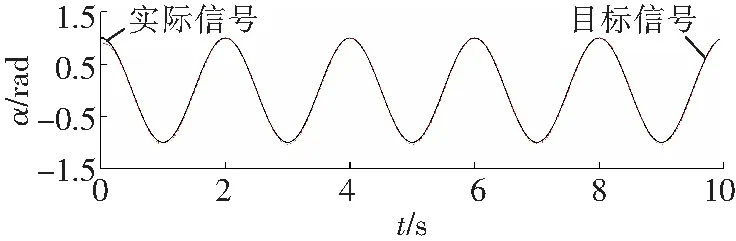
图4～6为滑模变结构控制器的控制效果，图7～9为RBF自适应滑模控制器的控制效果。

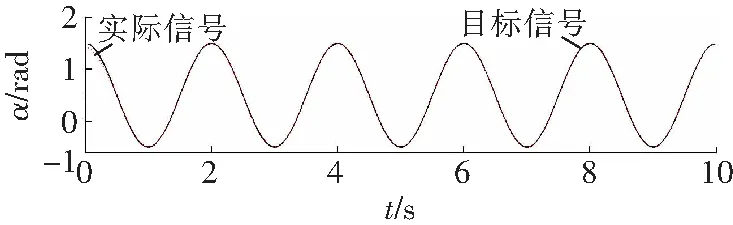
a 关节1

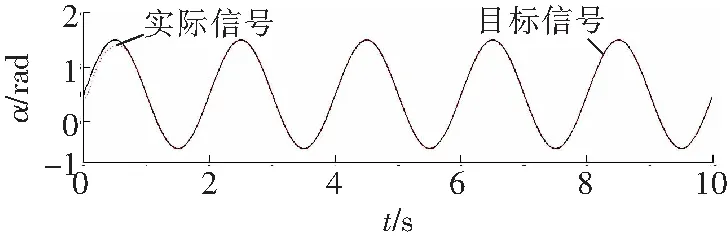
b 关节2

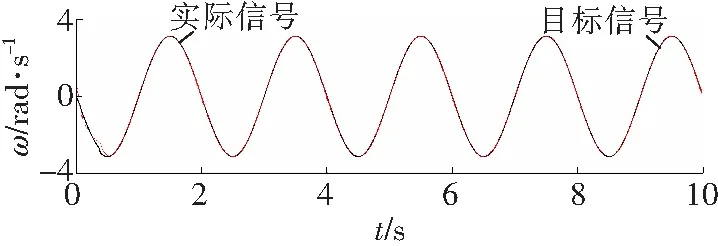
a 关节1

b 关节2

a 关节1

b 关节2

a 关节1

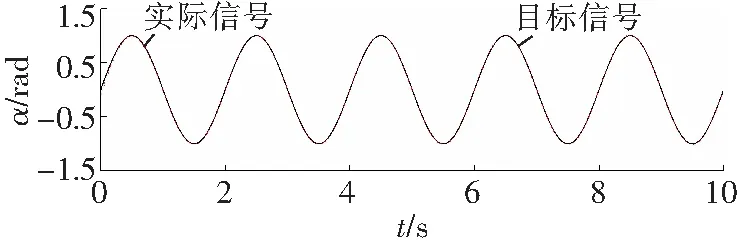
b 关节2

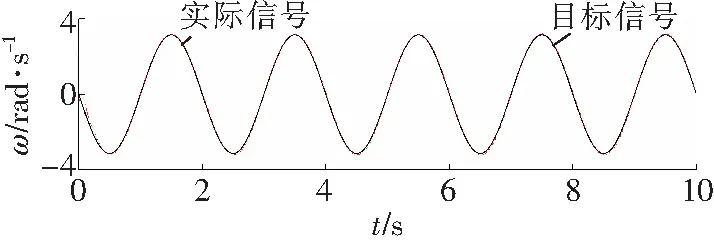
a 关节1

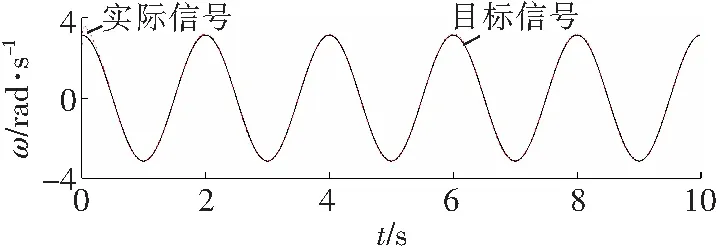
b 关节2

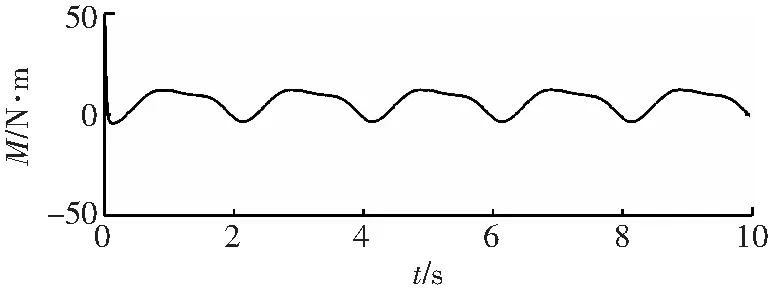
a 关节1

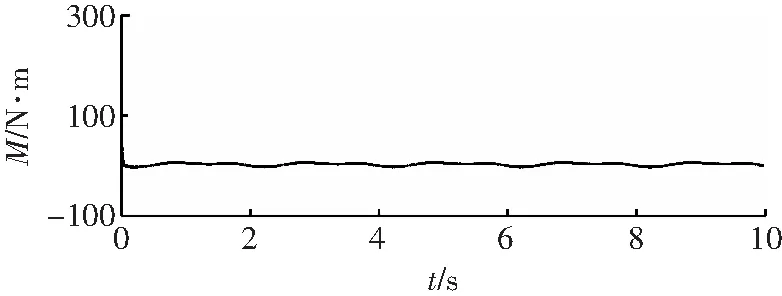
b 关节2

对比图4和图7可知，RBF自适应滑模控制器的角度跟踪更快速、跟踪精度更好。由图5和图8可知，RBF自适应滑模控制器的角速度跟踪速度更快，跟踪精度明显好于滑模变结构控制器的跟踪精度。图6显示滑模变结构控制器存在较明显的抖振，而在相同条件下图9所显示的RBF自适应滑模控制器的输出则明显削弱了抖振。综合分析图4至图9可知，相比一般的滑模变结构控制器，RBF自适应滑模控制器的效果更好。

4 结束语

RBF神经网络可以降低滑模控制器的抖振。在普通滑模变结构控制器的基础上，针对目前串联多关节机械臂模型中存在不确定因素的问题，利用RBF神经网络逼近模型中的不确定因素，增加鲁棒环节,以提高RBF网络的逼近精度，结合滑模变结构控制理论，建立RBF自适应滑模控制器，普通滑模变结构控制器和RBF自适应滑模控制器在跟踪精度、响应速度方面均能取得不错的效果；普通滑模变结构控制器虽然能够对串联多关节机械臂这类具有不确定性、耦合性的系统有一定的控制效果，但普通滑模变结构控制系统在控制过程中的抖振比较明显；引入RBF神经网络，能够根据模型不确定部分的变化以及干扰的影响，对控制器进行自适应调整，从而改善了控制器的品质，有效降低了滑模控制器的抖振。

设计的RBF自适应滑模控制器只验证了两关节串联机械臂的控制效果，对于实际应用中复杂程度更高的串联多关节机械臂的控制还有待研究。

[1] 霍 伟.机器人动力学与控制[M].北京: 高等教育出版社,2005: 165-174,452-453.

[2] 弓洪玮,郑 维.机器人轨迹跟踪的自适应模糊神经网络控制[J].计算机仿真,2010,27(8): 145-149.

[3] 王晓钰.W160 工业机器人的模糊滑模控制方法研究[D].哈尔滨: 哈尔滨工业大学，2012.

[4] Mohammad R F,Hadi D R,Dumitru B.A novel adaptive controller for two-degree of freedom polar robot with unknown perturbations[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(2): 1021-1030.

[5] 袁雷华.SCARA机械手的RBF神经网络自适应轨迹跟踪控制[D].武汉: 湖北工业大学，2012.

[6] 贾鹤鸣，宋文龙，郭 婧.基于神经网络滑模的采摘机械臂控制设计[J].吉林大学学报,2014,42(3): 709-713.

[7] 于靖军,刘辛军,丁希仑,等.机器人机构学的数学基础[M].北京: 机械工业出版社,2008: 372-378.

[8] 刘永青，袁祖强，戴加全，等.三关节机械臂运动精度的误差分析及补偿策略[J].机械设计,2014,31(3): 29-34.

[9] 叶锦华，吴海彬.不确定轮式移动机器人统一自适应神经网络 控制[J].中国机械工程,2017,28(2): 150-155.

[10] 窦立谦，田晓笛.基于自适应RBF神经网络的可重复使用运载器再入段姿态控制[J].航天控制,2017,35(1): 25-30.

[11] 杨 一,高社生,胡高歌.基于敏感度方差重要性的RBF神经网络结构优化算法[J].控制与决策,2015,30(8): 1394-1398.

(编辑 晁晓筠 校对 王 冬)

Research on RBFNN adaptive sliding mode control of serial manipulators

MinZhenhui,ChenHuanlin

(School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China)

This paper is aimed at overcoming the problems existing in the control of series manipulator.The study building on the RBFNN and sliding mode control consists of developing the RBFNN adaptive sliding mode controller,and the multi-joint robotic arm model,performing functional approximation of the uncertain factors of multi-joint robotic arm model using RBFNN and thereby establishing the stability of control system using the Lyapunov’s theorem.The research validates the controlling results of the common slide mode of controller and the RBFNN adaptive sliding mode controller using the position tracking controller of manipulator and simulating the two controllers.The results demonstrate that the proposed controller able to weaken the chattering affords a better control effect.

sliding mode control; manipulator；radial basis function neural network

2017-02-23

闵振辉(1979-)男，辽宁省抚顺人，讲师，硕士，研究方向：机电系统智能控制，E-mail:mzhacmilan@126.com。

10.3969/j.issn.2095-7262.2017.02.011

TP241

2095-7262(2017)02-0149-05

A