趣味生动化的全概率公式教学设计研究

周游

（湖南财政经济学院 数学与统计学院，湖南 长沙 410205）

趣味生动化的全概率公式教学设计研究

周游

（湖南财政经济学院 数学与统计学院，湖南 长沙 410205）

本文对全概率公式的新型教学模式进行研究，让授课更为趣味化、生动化.通过设置游戏、播放影片、设计调查问卷等新颖方式引入、阐述以及探究问题.选取学生感兴趣的实际问题，启发引导学生参与解决，使学生深化对全概率公式理解，掌握全概率公式应用技巧.

全概率公式；趣味生动；应用技巧

全概率公式是概率论与数理统计课程中一个非常重要的内容，在教学中要做到“法理相融”，即全概率的“算法”和“算理”的渗透理解.按照传统的教学模式，学生对该公式难以深入理解和掌握[1].因此，本次教学通过一个游戏的设置以及相关影片的放映，极大地激起学生的兴趣，与学生高度互动，让学生在玩乐中理解全概率公式的思想.典型问题教学启发、步步推导、与学生产生共鸣，增强学生的感知认识；选取学生感兴趣的彩票购买中奖、敏感性问题调查方式等问题，积极实施提问诱导，引导学生参与解决实际问题中，进一步深化对全概率公式理解，掌握全概率公式应用技巧[2-3].

1 问题引入：游戏和电影

1.1 情境创设，游戏引入

教师准备三个不透明的箱子和一张百元钞票.把钱放入某一个箱子中（只有教师知道钱在哪），现在请大家猜测.假如有同学猜测是1号箱，先不着急打开它，而从剩下的两个箱子当中，挑选一个没有钱的箱子，比如说2号箱，打开.这时候，给同学一个改选的机会，是坚持1号箱还是改选成3号箱？

思考：当教师首次打开一个没有钱的箱子时，同学是否应该改变初次选择？

1.2 师生互动，进行游戏

选择几位同学来进行游戏.并鼓励大家在课后进行这样的游戏，经过多次实验，把实验结果记录下来——总的试验次数是多少，坚持选择赢钱的次数和改变选择赢钱的次数分别是多少，尝试找到统计规律性.

1.3 播放影片，启发诱导

这看似是一个简单的游戏，实际上是一个严格的概率统计问题.这个问题兴起于上个世纪90年代，曾经在美国引起了非常广泛的兴趣和讨论，甚至还引起了美国中央情报局的关注，他们认为这个问题的分析解答可以应用到情报分析当中.播放《决胜21点》里面关于三门问题的一个片段.说明之前做的游戏实质上就是一个三门问题，即三个箱子表示三扇门，有钱代表门后有车，否则表示门后是羊[4].

电影给出了正确答案，但是大部分学生还没有完全理解，接下来教师给出数学推导.

1.4 问题求解，阐述思想

这个问题要解决的是是否改变初次选择，而是否改选取决于哪种情况下选中汽车的概率更大.

把改选“选中汽车”看作目标事件A，把初次选择的结果分别记为B1和B2，A受B1和B2的影响，即A=AB1∪AB2，由于这两个事件不可能同时发生，也就是说两者互不相容，根据互不相容事件并集的概率等于概率之和，A的概率就是这两部分的和.

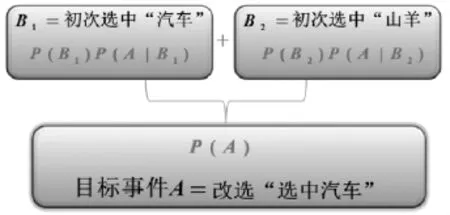
A=AB1∪AB2

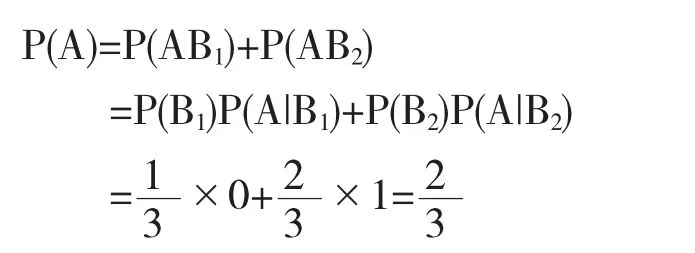
结论：当初次打开一扇有山羊的门时，是否应该改变初次选择？尽管不能保证一定能获得汽车，但是至少可以将获得汽车的概率从提高到.

内容小结：实际上，如果遇到一个复杂事件，直接去求概率可能比较困难，不妨将这个复杂事件分解为若干个简单事件来进行求解.这个问题的求解过程就是将一个复杂事件A分解为较为简单的两个事件AB1和AB2，然后将概率的加法公式和乘法公式结合起来，从而求得A事件的概率.全概率公式就是基于这样一种分解的思想.

2 全概率公式

2.1 阐述分解过程（PPT动画展示分解图示）

一般地，对于一个复杂事件A，要对其进行分解，首先要把整个样本空间分解为n个事件B1,B2, LBn，要求这n个事件之间是互斥的，并集是整个样本空间，也就是说B1,B2,LBn是样本空间S的一个完备事件组（划分）.由于样本空间的分解，事件A也被分解成了n个互斥的事件ABi(i=1,2,L,n)，因此，A可以表示这n个事件的并

2.2 推导公式（黑板演示推导过程）

2.3 全概率公式

定理 设事件组B1,B2,L,Bn是一个完备事件组，P(Bi)＞0，i=1,2,L,n,则对于任一事件A，

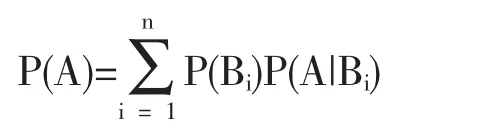
称为全概率公式[5].

说明：若把事件A看作结果，B1,B2,L,Bn就是导致该结果发生的原因，故全概率公式也称由因导果公式.其实质是结果在各原因下的条件概率的加权平均.

注意：全概率公式的思想是复杂问题的分解；关键是找到合适的划分.

3 解题步骤

3.1 实例引出

通过具体的实例来引导学生概括应用全概率公式解题的步骤.

引例 一位同学赶来上课，他可能乘坐地铁、公交或是出租车，乘坐这三种交通工具的概率分别为50%，30%和20%.已知乘坐这三种交通工具迟到的概率分别为0.05,0.2,0.1，求该同学迟到的概率.

分析：显然，乘坐这三种交通工具都有可能导致上课迟到，我们可以将迟到这一事件看作结果，记为事件A，它产生的原因有这三个，分别记为B1, B2,B3，而且，题目已知B1,B2,B3发生的概率，以及在B1,B2,B3发生的条件下A事件发生的概率，这是一个典型的已知原因求结果的问题，用全概率公式.

3.2 总结步骤

一、找到合适的完备事件组Bi(i=1,2,…,n)；二、求P(Bi)；三、求P(A|Bi)；四、利用全概率公式求目标事件A发生的概率.

4 例题精讲

4.1 彩票问题

生活中，同学们对彩票并不陌生.大家是否思考过这样一个问题：购买彩票的先后次序不同是否影响购买者的中奖概率？针对这个问题，引入下面简化的摸奖模型：

例1（摸奖模型） 设在10张彩票中有两张奖券，求第一个人和第二个人摸到奖券的概率分别是多少？

扩展：第三个人中奖的概率是多少？（复合实验）

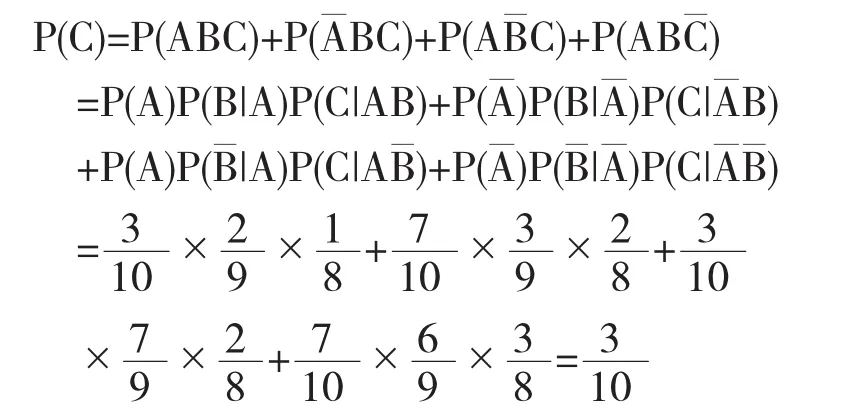
注意：在这个问题的解答当中可以看出，除了典型的已知原因求结果的问题，在这样的复合试验中也可以利用全概率公式，我们可以将最后一次的实验结果看作目标事件，前几次试验结果的交叉为样本空间的一个划分，根据全概率公式的思想，利用加法公式和乘法公式进行推导,得到全概率公式的拓展形式.

说明：中奖概率与购买次序无关.同样地，对于抽签问题，这个结论也是成立的.因此，无论是摸奖还是抽签，由于每个人获奖的机会都是相同的，大家无需争先恐后，安静地排好队依次抽取就好.

4.2 射击问题

学生练习：甲、乙、丙三人同时独立地对飞机进行射击，飞机被一人、两人、三人击中的概率分别为0.36,0.4和0.14，根据经验，飞机被一人击中而被击落的概率为0.2，被两人击中而被击落的概率为0.6，若三人都击中，飞机必定被击落.求飞机被击落的概率.

分析：飞机被击落是结果，原因分别是有一人、两人、三人击中飞机，直接用全概率公式计算.

将原题改为：

例2 甲、乙、丙三人同时独立地对飞机进行射击，三人中的概率分别为0.4，0.5，0.7.飞机被一人击中而被击落的概率为0.2，被两人击中而被击落的概率为0.6，若三人都击中，飞机必定被击落.求飞机被击落的概率[6].

分析：在该问题中，显然飞机被击落是结果，原因是有一人、两人、三人击中飞机，但是这三个原因的概率未知，还要先求解出来.

内容小结:在解决这一类问题的时候，一定要区分原因和结果.这里的原因就是样本空间的划分.

5 思考探究

要调查期末考试当中学生的作弊情况，直接利用是否作弊这种简单的调查问卷调查，其结果差强人意.对于敏感性问题，涉及到个人隐私，大家都不愿意说真话.现在请同学帮忙设计一种调查的方式，尽可能地保护大家的隐私.

教师提供一种方案：被测试者进入一个无人的房间，房中有一个箱子，箱子里有装有若干红球和白球，他从这个箱子随机抽出一个球，看过颜色后放回.如果取得白球，就回答：你的生日是在7月1日前吗？如果取得红球，就回答：你在期末考试中作弊了吗？将结果勾在一张只有“是”和“否”的答卷上.

请同学思考：为什么用这种方式大家愿意说真话？又怎样通过调查结果得到期末考试作弊率？

6 总结

这节课讲授了全概率公式这一重要公式.全概率公式是由加法公式和乘法公式结合起来的，公式应用的思想是复杂事件的分解，分解的关键是找到合适的划分.全概率公式也叫做由因导果公式，如果要由结果来探究产生的原因，那就要用到下一节内容——贝叶斯公式.

7 结束语

本次教学设计本着“让生活走进数学课堂、让数学回归生活”的理念，落实“以教师为主导，以学生为主体”的理念，在教学中尽可能突破传统模式，让授课更为趣味化、生动化.让学生在发现问题、分析问题、解决问题的过程中，建立了“用数学”的意识，培养了“用数学”的能力，体验了“用数学”的乐趣，教学效果良好.

〔1〕赵云平.关于全概率公式的教学探析[J].农村经济与科技,2016,27(22):239-241.

〔2〕冯卫东.情境教学操作全手册[M].南京：江苏教育出版社,2010.

〔3〕秦玉芳,丁艳凤,郑小琪.浅谈情境教学法在概率统计中的应用[J].高教学刊,2016（15）:113-114.

〔4〕张慧.关于“概率论与数理统计”课程中案例教学的研究[J].求知导刊,2015,24:136.

〔5〕刘宏超.概率论与数理统计[M].北京：清华大学出版社,2011.

〔6〕吉家锋.在课堂上巧妙嵌入有趣教学实例,提高学生学习全概率公式的兴趣和质量[J].高等教育研究,2014,31(3):32-34.

G642.4

A

1673-260X（2017）04-0219-03

2017-02-03

湖南省教育厅科学研究项目(14C0192);湖南财政经济学院教学改革项目(2016xjjg006)