例析四步解题教学法的运用
2017-05-10王祥表
王祥表
(浙江省宁波市奉化区剡溪中学)
例析四步解题教学法的运用
王祥表
(浙江省宁波市奉化区剡溪中学)
为了“不露痕迹”地帮助学生,发展学生自身的内蕴能力,探寻学生的发展之路,在一道几何例题一课的教学中,运用波利亚的解题教学“四步法”,进行了多角度地启发式教学,形成了一些思考与感悟.
解题教学;四步法;启发与感悟
教师最重要的任务之一是帮助他的学生.要做到这一点,教师应当谨慎地、不露痕迹地帮助学生.为此,笔者根据波利亚解题理论的四步法,并通过一道例题谈谈如何在教学过程中做到顺其自然、“不露痕迹”.
一、例题呈现
例 如图1,等边△OAB的边AB与y轴交于点C,点A是反比例函数的图象上一点,且BC=2AC,求等边△OAB的边长.
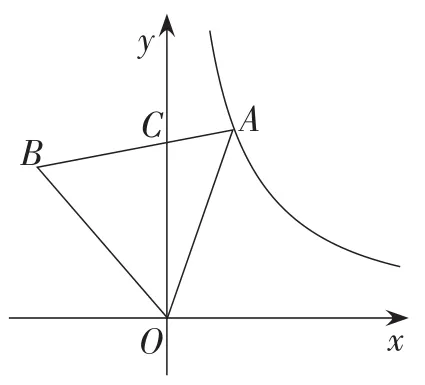
图1
基于学情,如果把该题作为例题直接呈现给学生,教学过程可能举步维艰.所以,笔者结合学生已有的知识水平,事先搭一个“脚手架”.
二、四步法教学过程展示
引例 如图2,等腰Rt△OAB的底边AB与y轴交于点C,点A是反比例函数的图象上一点,且BC=2AC,求等腰Rt△OAB的腰长.
该题的难度已经明显降低,以此作为铺垫,学生稍加思考,即可运用“三垂直模型”拟定出解题方案.
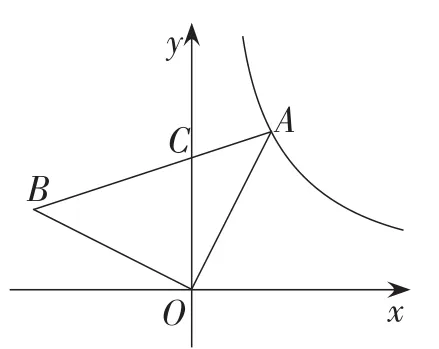
图2
此时,即可呈现例题,并根据波利亚的《怎样解题》表,对该题分成四个步骤.
第一步:理清题意
理清题意,并引入适当的符号,把条件(或从条件直接推导出来的结论)标注在原图上.
(1)AB=BO=OA;∠BAO=∠ABO=∠AOB=60°;∠BOC+∠AOC=60°.若过点O作OD⊥AB,垂足为点D,或过点C作CE⊥AO,垂足为点E,都能产生特殊直角三角形.
(3)令AC=a,则BC=2a.
第二步:拟定计划
(1)以构造“三垂直”模型为切入点.
根据引例,学生的思路或许已经无意识地朝着如何构造“三垂直”模型的方向迁移了.
方案1:如图3,过点O作 OD⊥AB,垂足为点D,再过点D作DE⊥Ox,垂足为点E,并过点A作AF⊥ED,垂足为点F,交y轴于点G.
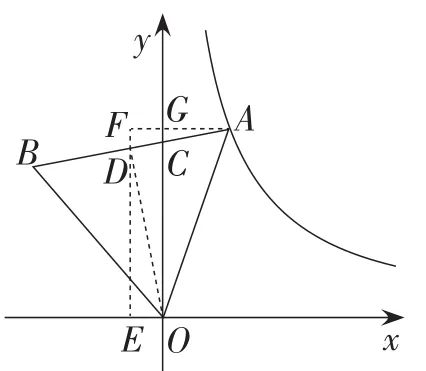
图3
因为BC=2AC,而D为AB的中点,
则AF=3FG,OE=FG.
再由EF=OG,列出方程,即可求解.
方案2:如图4,过点B作BE⊥Oy,垂足为点E,再把Rt△BOE绕着点O顺时针旋转60°,得到Rt△AOH,分别过点A和点H,作AD⊥Oy,HG⊥Ox,并将它们反向延长,交于点F,即得Rt△AFH∽Rt△HGO.

图4
基础再扎实一点的学生或许还能想到三垂直模型的“升级版”,即“一线三等角”模型.
方案3:如图5,可以作∠BDO=∠AEO=∠AOB=60°,过点B分别作BG⊥Oy,BH⊥Ox,过点A分别作AF⊥Oy,AI⊥Ox.
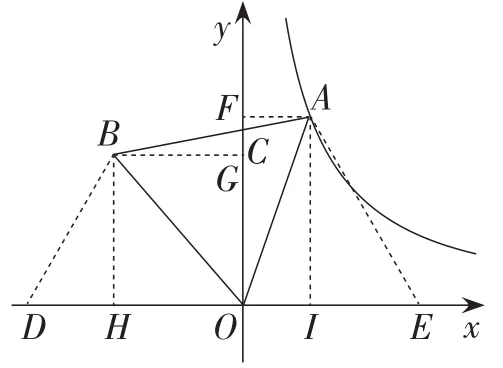
图5
再证明△BOD≌△OAE,可列得方程求解.
(2)以条件(1)(3)为切入口.
为了不使学生的思维产生负迁移,教师可适时设问:除了运用这一基本模型解决该题外,我们能否从“等边△OAB”自身的特殊性并结合条件“BC=2AC”为切入口呢?
方案4:如图6,过点A作AD⊥Oy,垂足为点D,过点C作CE⊥AO,垂足为点E.
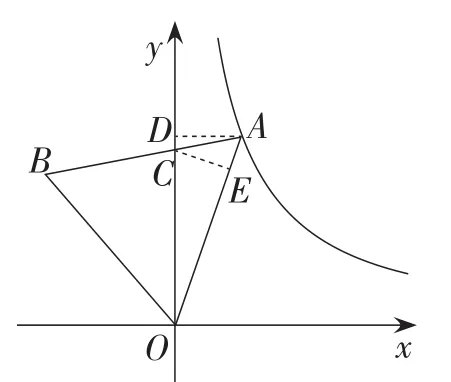
图6
因为△OAB为等边三角形,
所以∠BAO=60°.
根据Rt△AOD∽Rt△COE,可列得方程求解.
第三步:执行计划
选择自己认为思路清晰的一种拟定方案,把每一步按照方案清楚地表达出来,并注意检查每一步的正确性.
第四步:回顾
解答完成后,再次回顾整个过程,重新斟酌、审查结果和推导结果的过程.同时,教师追问也紧随其后.
师:在例题的方案1~3中,都用到了一个怎样的基本图形?
生2:三垂直(一线三等角)模型.
师:如果只从辅助线的特征来说,观察三种方案(包括引例)的辅助线有什么共同点?
生2:基本都是竖直的或水平的.
师:你在以前学过的哪些题目中也是可以这样去画的?
生2:平面直角坐标系中求任意两点的距离,或是三角形、四边形等求一些面积问题时.
师:的确如此.在很多时候,平面直角坐标系中的一些问题,如果要画辅助线往往都会遵循化倾斜为纵横的原则.
自此,在教师不断地启发追问下,学生对已学知识的结构体系已逐步建立起来,思想方法也在随之内化.
三、教学感悟
1.铺设应顺势
《义务教育数学课程标准(2011年版)》明确要求:教师教学应该以学生的认知发展水平和已有的经验为基础,面向全体学生,注重启发式和因材施教.正如上述的铺设,就是基于对学情的考虑.如果直接呈现例题,那就远远高于学生已有的认知水平了.所以笔者在教学中以引例作为“脚手架”,从而轻松地帮助学生穿越了“最近发展区”.但需要特别注意的是:“脚手架”虽好,但也不能为其所累.因为一旦搭了“脚手架”,即产生了“沉锚效应”,也就是思维定势.要想突破定势,实现思维正迁移,就要另辟蹊径,就如上述方案4的提出一样,才能打破学生的惯性思维.
2.启发需适时
波利亚的怎样解题表是“现代启发法”纲领和解题艺术的大成.而在解题教学中,成功与否,很大程度上就取决于“启发式的过程分析”,即一个个适时的追问.因此,教师要把握追问的时机,在面对一道有难度的试题时,联想到学生能解决的与之相关联的题目,在不断改变题目条件的基础上,唤醒学生已有的知识,在“不露痕迹”的追问中,帮助学生顺利完成思考.
3.感悟在自然
解题基本功由知识因素、能力因素、经验因素和非智力因素四部分组成.前两者或许学生马上能够习得,但是后两者不是一朝一夕就能获得的,它们需要学生在一个长期的潜移默化的过程中去不断体验和感悟.然而在这一过程中,教师最好顺其自然地帮助学生,让学生感受到“这正是学生自己原本应该想到的”.任何的数学思想方法或是活动经验都不需要教师在教学中刻意地贴标签式的去讲述,而是让其如细水一般在教学过程中缓缓流淌,润物无声.
“教,是为了不教”,教师一开始就应提醒自己“我要为学生离开我能独自学习做准备”.
努力做到想学生之所想,教学生之所需.在解题教学中,重视教学过程的“无痕”展开.
让铺设“无痕”,在顺其自然中,认知结构得以迁移;
让启发“无痕”,在循序渐进时,解题思维得以提升;
让感悟“无痕”,在潜移默化间,思想方法得以渗透.
[1]波利亚.怎样解题:数学思维的新方法[M].徐鸿,冯承天,译.上海:上海科技教育出版社,2011.
2017—02—01
王祥表(1983—),男,中学一级教师,主要从事初中数学教育教学研究.
