巧构“几何直观” 共享直观“三味”——从常规解答的反思中谈图象选择题解答

戴向阳

（安徽省安庆市宜秀区五横初级中学）

巧构“几何直观” 共享直观“三味”
——从常规解答的反思中谈图象选择题解答

戴向阳

（安徽省安庆市宜秀区五横初级中学）

几何动态图象选择题，是近年来涌现出来的难度较大的试题.通常是先确定函数解析式再认定图象，既烦琐又耗时，造成考场低分值与高时耗冲突.利用“几何直观”帮忙选择图象，实现“秒杀”，解决高时耗与低分值的矛盾.通过三道例题，立足不同视野，构造“几何直观”解答选择题，展示“几何直观”神奇的解题效用.

几何动态图象；常规解答；几何直观；合情推理

几何动态函数图象选择题，是近年来中考的一大亮点、难点.尤其是一些没有数据的曲线型图象，即使是排除法也无法下“口”.这类图象多是宏观、粗略地反映几何动态变化，按常规方法：先求出函数解析式，再依据熟知的函数性质得出图象.这常常会耗时很久，更有甚者，有的函数解析式在初中阶段无法求解.实质上，正是这些没有数据的大致图象，却暗藏着“秒杀”的玄机——“几何直观”，因为初中阶段的“几何直观”正是以感性认识为基础的，注重的是合情推理，讲究以粗略对付粗略.

下面先从对一道试题的常规解法的反思说起.

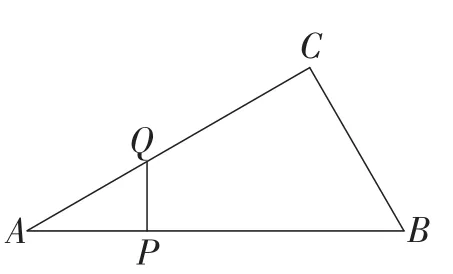
图1

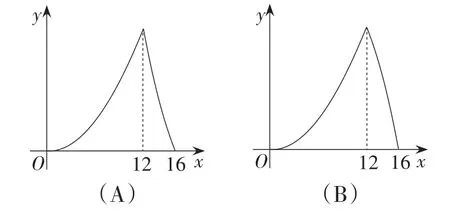
题目 （2014年山东·泰安卷）如图1，在△ABC中，∠ACB=90°，∠A=30°，AB=16.点P是斜边AB上一点.过点P作PQ⊥AB，垂足为点P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（ ）.

一、 常规解答

当点Q在AC上时，因为∠A=30°，AP=x，

当点Q在BC上时，如图2所示.

因为AP=x，AB=16，∠A=30°，

图2

所以BP=16-x，∠B=60°.

所以该函数图象前半部分是抛物线，开口向上，后半部分也为抛物线，开口向下.

故选B.

二、反思解答

从上述解答不难看出，此题难度较大，表现在以下几个方面：（1）它是一个动点问题，问题在变化中，与静态问题相比，学生难以把握；（2）涉及分类讨论，它需要学生有缜密的思维，准确把握动态问题“临界点”的洞察力；（3）面积的表示，尤其是点Q在BC上时，△APQ的面积如何表示？如何对接x与高PQ的关系？这是解题的关键所在.另一方面此题涉猎的知识点非常广泛：特殊三角函数值，解直角三角形，求函数解析式，函数与函数图象的性质，等等.由此可见，此题是一道综合性很强的函数应用性问题，从“触”题到成功解题，以考场宝贵“时间”来衡量，此题当值更多分数.这种常规方法，作为4分的选择题是否有点“小题大做”了呢？是否有更好的“秒杀”方法呢？回答是肯定的，“几何直观”便是这类问题的“杀手锏”.

三、几何直观

《义务教育数学课程标准（2011年版）》（以下简称《标准》）中“几何直观”成为数学课堂教学关注的关键词.《标准》明确道出“几何直观”的作用——几何直观是指利用图形描述和分析问题.借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路、预测结果.可以帮助学生直观地理解数学.函数解析式是微观、精细刻画函数图象，“几何直观”在于宏观、粗略反映函数图象，当图象不注重于“精微”刻画时，可构建“几何直观”“合情推理”，快速有效选取图象.下面具体分享“几何直观”不一样的“神味”.

1.以彼观此，直观面积，显其“简”

当问题的研究对象丧失“直观”时，不妨从与其相关的周边对象构建“几何直观”，起到以彼攻此的目的.对于面积类问题，如果借助“几何直观”，解题会如虎添翼，较之常规，其“简”不言而喻.

题目紧扣点C“分界点”，多数学生能锁定正确选项在选项A、选项B中.当点Q在AC上向点C运动时，不难构造“直观”，感受△APQ的面积变化幅度，△APQ的面积增大的幅度越来越大；当点Q在CB上向点B运动时，虽然可以“直观”感受到△APQ的面积在减小，但面积减小的幅度却不“直观”.

那么如何构造“几何直观”反映这种变化幅度呢？将目光盯在△APQ上，是难以直观的.如果旁观△ACQ与△QPB，就豁然开朗了.如图3，当PP1=P1P2时，QQ1=Q1Q2.当点P运动到点P1，P2时，△ACQ面积匀速增大，由于梯形P1P2Q2Q1的面积＜梯形PP1Q1Q的面积，所以△QPB的面积减小的幅度越来越小，从而S△ACQ+ S△QPB增加的幅度越来越大，所以△APQ的面积减少的幅度越来越大.故选B.

图3

2.矮摘高桃，直观线段，凸其“奇”

数学解题的高明之处不在于用高深的知识去回答低端问题，而在于用低年级知识回答高年级问题，即“机枪打飞机”.对于缺失直观的变化线段，也可以用“几何直观”托起，这正是“几何直观”的“奇”趣所在.

例1（2014年山东·潍坊卷）如图4，已知矩形ABCD的长AB为5，宽BC为4.E是BC边上的一个动点，AE⊥EF，EF交CD于点F.设BE=x，FC=y，则点E从点B运动到点C时，能表示y关于x的函数关系的大致图象是（ ）.

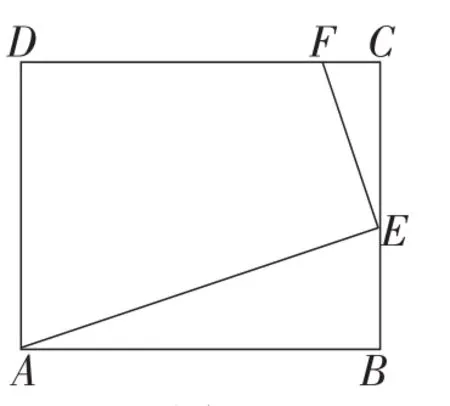
图4

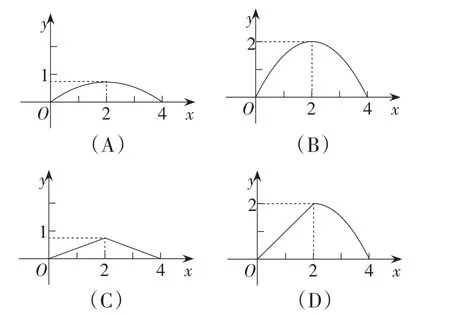
思考：此题常规解答多是通过△ABE∽△ECF，求出y与x的函数关系式达到解题的目的.能否抛开函数关系式，站在更低端知识上，让FC的变化直观化呢？

如图5，经过三角形全等的学习可知，△ECF可视作从△ABE中截得的△AHG部分.FC大小可通过GH来描述.y的大小，表现为点G的高度.y与x的函数关系，表现为点G随x变化时的位置.

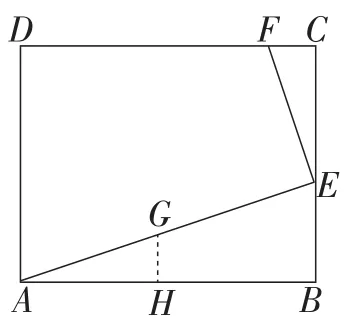
图5

所以只要描出点G随BE（即x）变化时若干位置即可.

由于AH=EC=4-x，随着x的增大，AH在减小，这时点G水平向左（即向点A）运动，这与通常随x的增大，图象上点在水平方向上向右运动相矛盾.

如何解决这一矛盾呢？

只需将图5沿BC翻转180°，并建立平面直角坐标系.将线段AB十等分，线段BC八等分，制成网格（如图6）.

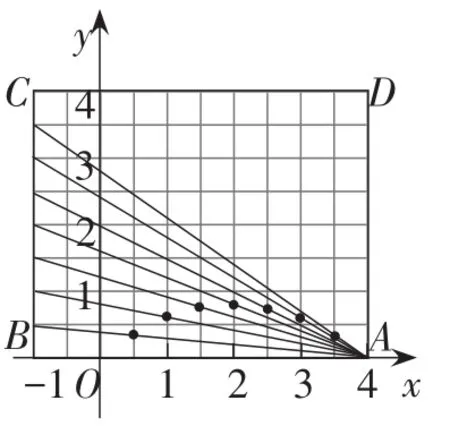
图6

分别将A（4，0）与（-1，0.5），（-1，1），（-1，1.5），（-1，2），（-1，2.5），（-1，3），（-1，3.5）连接起来，依次与直线x=0.5、直线x=1、直线x=1.5、直线x=2、直线x=2.5、直线x=3、直线x=3.5相交，这些交点形成的图象，就是点G随BE（即x）变化时的图象，即y与x的函数图象.

故选A.

3.巧立参照，直观涉高，彰其“妙”

巧立杠杆可省力，数学解题可巧借参照线，通过参照线的“直观”观摩问题，可事半功倍.在涉高问题中，如能“立”好参照，用好几何直观，其解答之简练“妙”不可言.

例2（2014年湖北·黄石卷）如图7，AB是半圆O的直径，点P从点A出发，沿半圆顺时针方向匀速移动至点B，运动时间为t，△ABP的面积为S，则下列图象能大致刻画S与t之间的关系的是（ ）.

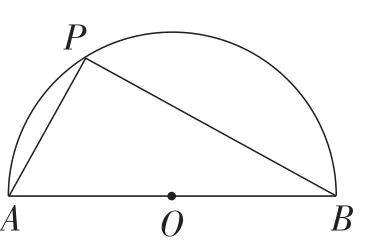
图7

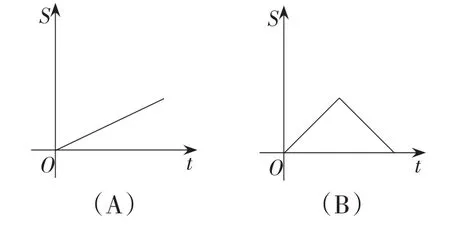
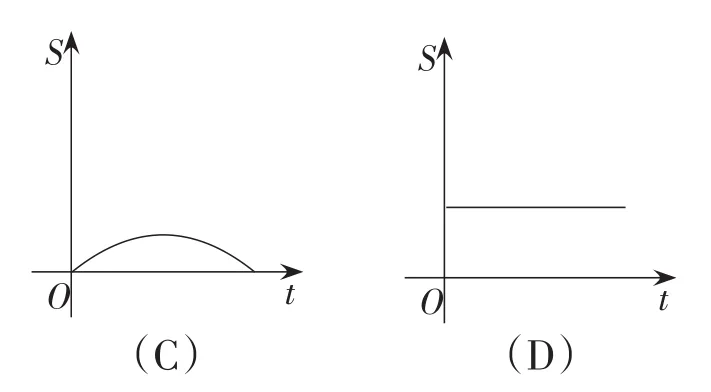
思考：此题在初中阶段无法求出S与t之间的函数关系式，虽然涉高，但各选项差异较大，答题的门槛很低，学生完全可凭直觉正确答题.选项A、选项D可直接排除，学生常徘徊于选项B、选项C之间，且倾向于选项C.问题是为什么选项B不可以？如果增加一个如图8所示的干扰选项，该怎么办？

图8

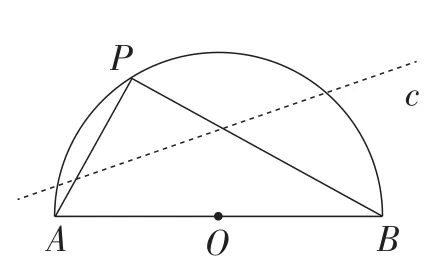
图9

对于选项B，可借用一条直线，构建图9来直观感受，当点P沿直线c匀速向右运动时，点P到AB的距离随时间t匀速增大，即△ABP的高匀速增大，由于底AB不变，所△ABP的面积匀速增大，即△ABP面积与时间t成一次函数关系.故当点P在直线c外沿弧运动时，△ABP的高不可能匀速增大，所以△ABP的面积与时间t不成一次函数关系.故选项B不正确.

图10

如果试题选项中是图8与选项C，这时学生就两难了，能否利用“几何直观”，做出正确选择呢？如图10，将半圆弧八等分，很明显各平行线间距离从下向上依次减少（如果不明显，可将圆画大些，将份数分少些，这时差异会更明显）.即当点P匀速从点A到点C，D，E，F运动时，△ABP的高增加的幅度越来越小；当点P匀速从点F到点G，H，I，B运动时，△ABP的高减少的幅度越来越大.从而当点P从点A沿匀速运动时，△ABP面积增加的幅度越来越小；当点P从点F沿匀速运动时，△ABP面积减少的幅度越来越大，所以选项C符合，而图8表示幅度先增加的越来越大，再减少的越来越小.

四、解后反思

长期以来一线教师认为“几何直观”在解题中作用有限，解题教学中致力于对函数解析式的追求，忽视了对学生“几何直观”能力的培养，遇到无法求解的解析式便责备超纲、涉高.殊不知“几何直观”对一名学生的数学感知能力的重要性，数学发现与数学感知能力息息相关.很多教师狭隘的认为“几何直观”仅仅能解决某些面积变化类图象：对于题目，当点Q在AC上时，尚能构造“几何直观”解答；当点Q在BC上时，便爱莫能助了.很明显，这归因为思维单一不灵活.实质上转换一下思维的视角，就会厚爱“几何直观”了.题目放眼旁边三角形，BC段直观就浮出来了；例1着眼于全等“矮树枝”，以低端的八年级上册知识轻松摘取高端的九年级“鲜桃”；例2巧借直线c轻松排除选项B，涉高不足畏.可见“几何直观”作用之广，不单能解决简单面积，还可以解决复杂的面积，甚而线段或涉高题.巧构直观解答图象选择题，往往会收到神效——“简约”“奇趣”“美妙”，令人耳目一新.

［1］孔凡哲.关于几何直观的若干认识误区及其矫正［J］.中学数学教学参考（中旬），2014（6）：2-5.

［2］金绍鑫.“涉高题”解法要避免涉高［J］.中学数学教学参考（中旬），2015（1/2）：60-62.

2017—02—19

戴向阳（1974—），男，中学一级教师，安庆市骨干教师，数学学科带头人，主要从事教育教学与解题研究.