“以学为中心”的有效数学课堂的构建
——贲友林老师《圆的认识》教学片断赏析
2017-05-05徐黎明
徐黎明
“以学为中心”的课堂,就是以生为本,以学为主的课堂,是学生通过自主学习、小组合作等学习方式进行问题探究,是教师组织指导,有效引领,高效达标的课堂。苏霍姆林斯基说过:“在人的心灵深处都有一种根深蒂固的需要,就是希望自己是一个发现者、研究者、探索者。”
【片断一】引入:初步感知圆
师:关于圆,知道了什么?
(学生思考后,交流汇报)
生:圆和多边形都是平面图形。
生:圆是一种几何图形,它有半径、直径、圆心。
生:圆有无数条半径、直径。
生:圆没有直线,只有曲线。
生:圆上的点到圆心距离相等。
生:圆有无数条对称轴。
生:圆上任意两点之间的部分叫弧。
生:画圆要找圆心。
【赏析:上课伊始,贲老师请听课老师随机抽出一个学号30号,由学号30号学生来请其他同学回答问题。贲老师主动把课堂让给学生,让学生真正成为学习的主人。贲老师精心设计问题,在学生的回答中,可以初步知道学生对圆有哪些了解。从学生的交流中,可以看出学生课前的预习很重要。有效的预习使学生明白新课要学习的知识中有哪些知识点自己还不是很清楚,能够提出什么问题。导入新课时,贲老师放手让学生来请学生回答,学生在轻松的氛围中展开学习。】
【片断二】操作:画圆的步骤
师:认识了圆,会用圆规画圆的举手?
教师请一名学生用圆规试着画出一个圆。
师:要注意什么?大家一边看一边想。
生:针尖固定的没有动。
师:手抓圆规的头,有头就有脚。你能看到不动的地方吗?什么不动?
师:半径在哪里?
生:两脚之间的距离是半径,这个长度不能动。
【赏析:在教学用圆规画圆时,贲老师先了解班级里有哪些学生已经会用圆规画圆,同时请学号是8号的学生现场展示用圆规画圆。其余学生在看8号同学画圆时通过观察发现针尖是一个固定的点,这个点位置没有发生变化。学生找出了“定点”这一步后,接着让学生在交流中发现圆规两脚之间的距离也没有变化。用手抓住圆规的“头”,旋转一周就能画出一个完整的圆。学生在自主探索中知道画圆的步骤:定点、定长、旋转。贲老师让学生以研究的方式来学习数学,让教师的教服务于学生的学,进而体现了“以学为中心”的教学理念。】
【片断三】探究:触摸圆特征
师:谁能找出所画圆的圆心?
生:针尖上的那一点,就是圆心O。
(学生画出一条半径)
师:半径是什么?
生:半径是一条线段。
师:线段有两个端点,圆的直径是什么?
生:直径也是一条线段。
师:直径为什么不是直线?在圆上面从哪到哪是直径?哪两个端点?有补充吗?
教师用直尺在圆上进行摆放。这样画是直径吗?
生:要经过这个圆的圆心。
师:现在画了几条半径?
生:3条半径。
生:1条半径。
生:我认为是3条半径,1条直径可以分成2条半径。
师:还可以画多少条半径和多少条直径?
生:可以画无数条半径和直径,而且直径的长度是半径的2倍,半径长度是直径的一半。
师:圆心写在哪里?
生:圆心在圆的中心,就是画圆时,针尖所在的点。
师:定长是什么?定长3cm,这3cm指的是什么?
生:是指画的圆半径是3cm。
师:我要画一个圆半径2cm,圆规两脚间的距离是多少?
生:2cm。
师:谁能说一说,什么是圆的对称轴?
生:直径所在的直线就是对称轴。
【赏析:在学习圆的各部分名称时,先让学生找出所画圆的圆心,就是画圆时针尖固定的一点,可以用字母O表示。贲老师让学生在圆上试着画出一些半径。在交流中知道半径是连接圆心到圆上任意一点的线段。在画半径时,有名学生画出的是直径,是通过圆心并且两端都在圆上的线段。画圆的直径时,贲老师用直尺放在圆上,上下移动直尺时,让学生判断画出的线段是不是直径。学生根据是否通过圆心来判断直尺所在的线段是不是直径。在同一圆内画了一条半径和一条直径后,贲老师问学生有几条半径,这是一个看似简单,其实蕴含着半径与直径之间长度关系的问题。一条直径可以分成两条半径,这样半径与直径的关系就呈现出来。在圆中有无数条半径,有无数条直径。画圆时定点后就要定长,定长就是确定圆规两脚间的距离,即确定圆的半径长度。圆是轴对称图形,有无数条对称轴。对称轴是一条直线,圆的对称轴是圆的直径所在的直线,就是它的对称轴。学生明白了圆的直径有无数条,圆的对称轴也有无数条。】
【片断四】反馈:按要求画圆
画圆:1.点A在圆上。
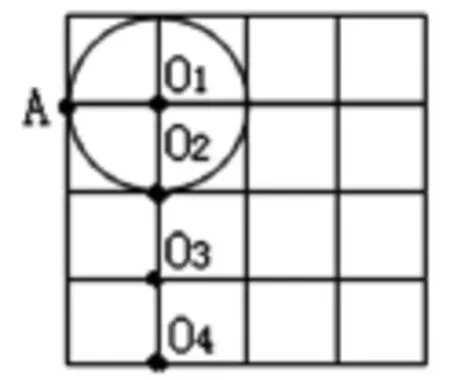
生:画出如图中的圆O1。
师:还有不同的画法吗?只要标出圆心,不用画出来。
生:接着又标出了圆心O2、O3、O4。
师:这三个圆大小一样吗?
生:大小不一样。
师:由此可以看出哪个圆最大?圆的大小由谁来决定?
生:圆的大小由半径(或是直径)来决定。
师:圆的位置又由谁来决定呢?
生:圆心。
画圆:2.点A、B都在圆上。

画圆:3.点 A、B、C 都在圆上,先找出点C,再画出圆。
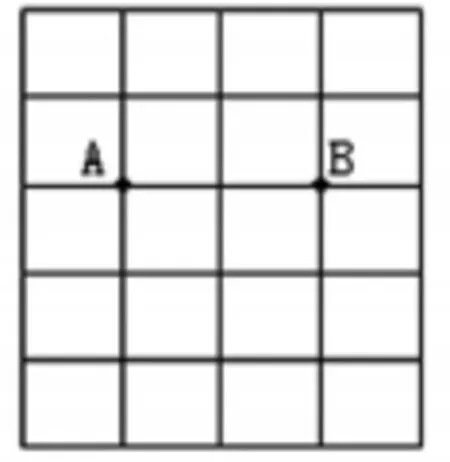
【赏析:在练习环节,贲老师精心设计了一组题,不但有效巩固了学生所学的知识,而且提升了学生的思维能力。贲老师设计的这组题,由浅入深,层层推进。问题一先让学生画出有一个已知点在圆上的圆,学生根据要求可以画出多个符合要求的圆,画出的不同圆的大小也是不一样的。贲老师让学生回答圆的大小由什么决定,学生在自己的画图中,可以感知到圆的大小是由圆的半径来决定的。问题二要求画出点A、B都在圆上,学生在画出不同的圆进行观察时会发现要使A、B两点都在圆上,这些圆心都在线段AB的对称轴上面。问题三的设计,进一步提升学生的思维能力。学生需要综合运用到所学圆的知识来进行解答。】
