(语言)Heronian平均算子及其决策应用

刘卫锋，常 娟，杜迎雪

(郑州航空工业管理学院理学院，河南 郑州 450015)



(语言)Heronian平均算子及其决策应用

刘卫锋，常 娟，杜迎雪

(郑州航空工业管理学院理学院，河南 郑州 450015)

多属性决策中的许多集成算子假设属性相互独立，从而导致信息集成和决策结果出现不合理的情况。Heronian平均算子是一种体现属性间相互作用的集成算子，因此研究和推广Heronian平均算子具有重要的理论和现实意义。首先，针对相关文献中的加权Heronian平均算子不具有还原性，定义了一种具有还原性的广义加权Heronian平均算子(GWHM)，随后定义了三参量Heronian平均算子(TPHM)和三参量加权Heronian平均算子(TPWHM)，并分别研究了它们的幂等性、单调性和有界性等性质。然后，将GWHM算子、TPHM算子和TPWHM算子分别推广到语言决策中，给出了语言加权Heronian平均算子(LWHM)以及三参量语言Heronian平均算子(TPLHM)和三参量语言加权Heronian平均算子(TPLWHM)，并对它们的性质进行了探讨。最后，给出了利用(语言)Heronian平均算子进行决策的方法，并通过两个实例说明了方法的可行性。

集成算子；Heronian平均算子；语言Heronian平均算子；决策

1 引言

有效集成属性值是多属性决策的一个核心问题。针对该问题，人们进行了积极地研究，提出了许多可行有效的集成算子，诸如WA算子[1]、WG算子[2]、OWA算子[3]、OWG算子[4]、OWH算子[5]、QOWA算子[6]、Bonferroni平均算子[7]、Heronian平均算子[8]，等等。为了适应不同的决策环境，人们将这些集成算子推广到不同决策领域，形成了具有不同特色、适合不同决策环境的各类集成算子。于是,按照决策信息环境不同，可以将集成算子大概分为以下几类: (1)实数集成算子；(2)区间数集成算子；(3)模糊集成算子、(4)直觉模糊集成算子；(5)犹豫模糊集成算子；(6)语言集成算子；等。实数集成算子适用于属性值为实数的决策环境，是最基本的信息集成算子，也是研究成果最为丰富的集成算子,其他类型集成算子一般由实数集成算子延拓扩展而得到。除了Harasnyi等[1-8]中常见的几种实数集成算子，还包括Yager等[9-15]中分别定义的GBM平均算子、TPBM算子、TPGBM算子、TPGBGM算子、BGM算子以及PHM算子和GHM算子，等。区间数集成算子是实数集成算子的推广，其能够有效集成区间数决策信息。目前关于区间数集成算子的相关研究也取得了丰硕的成果[16-24],包括: UOWA算子、 UOWG算子、COWA算子、COWG算子、UBM算子、IHM算子，等。当决策属性值难以使用实数和区间数进行表达以及考虑到决策者思维本身所具有的固有模糊性时，Bellman等[25]提出使用模糊数表达方案满足属性的程度评估值，于是出现了处理模糊信息的各种模糊集成算子[26-30]，模糊集成算子具有较强的灵活性和适用性，目前模糊集成算子主要有：FOWA算子、FOWG算子、TFOWA算子以及TFBM算子，等。直觉模糊集成算子适用于属性值为直觉模糊数的决策环境，此类集成算子既能体现出决策者对方案满足属性的评估值，又能体现出决策者对方案不满足属性的评估值，因此直觉模糊集成算子较模糊集成算子更灵活，应用范围也更广。目前常用的直觉模糊集成算子有[31-37]：IFOWA算子、IFOWG算子、IVFOWA算子、IVFOWG算子、IFBM算子、IVFBM算子以及IFHM算子和IVIFHM算子，等。尽管模糊集成算子和直觉模糊集成算子在处理决策模糊信息时较其他集成算子优势更明显，但也会面临一些问题，比如，在实际决策过程中，决策者评估方案在属性下的偏好时，可能出现在一些评估值之间犹豫不决的情况，此时使用模糊数与直觉模糊数表示偏好就无能无力了，但是使用符合决策实际的犹豫模糊数[38]就能够轻而易举解决此问题。针对决策信息为犹豫模糊数的决策问题，人们提出了许多犹豫模糊集成算子，主要有[39-44]：HFPA算子、HFG算子、HFBM算子、HFGBM算子和GHFBM算子，等。在多属性决策中，人们常常喜欢直接使用“优”、“良”、“中”、“差”等语言对评价对象的某种属性进行评价，故研究以语言为属性值的信息集成算子具有重要意义。目前关于语言集成算子的研究也取得了丰硕成果[45-54]，常用的集成算子有：LOWA算子，LHA算子，EOWA算子，EOWG算子，GILA算子，ULA算子，IULOWA算子，ULHM算子及2TLBA算子和W2TLBA算子，UPLHHA算子，等。最后，一些将不同信息进行融合的集成算子也值得我们注意，比如，王坚强和吴建文[55]通过定义区间灰色不确定语言及其运算法则和距离公式，提出了区间灰色不确定语言的IGULOWC-OWA算子,并提出了相应的决策方法；Liu Peide等[56]将直觉模糊与不确定语言Heronian平均相结合，提出了IULHM集成算子。

按照决策信息环境将集成算子进行分类，有助于人们根据决策信息实际情况选择合适的集成算子，但是也存在一定的局限性，比如,没有考虑到属性之间是否存在相互作用关系。而事实上，在决策应用中，属性之间往往并非相互独立,而常常存在着相互作用的关系，因此按照集成算子属性间是否具有相互作用关系来考虑集成算子的分类，以及研究反映属性值之间相互作用关系的集成算子均具有十分重要的现实背景和理论意义。显然，从属性之间是否具有相互作用的角度来看,现有的集成算子可以分为两大类:一类是属性间相互独立的集成算子；一类是考虑属性间相互作用的集成算子。在实际决策应用中，我们使用的大部分集成算子是假设属性间相互独立的，如Harasnyi等[1-6]中的实数集成算子以及由此拓展而得到区间数集成算子[16-22]、模糊集成算子[26-29]、直觉模糊集集成算子[31-34]、犹豫模糊集成算子[39-44]和语言集成算子[45-51，54]，等等。而Bonferroni和Boliakov等[7,8]中定义的Bonferroni平均算子和Heronian平均算子以及由此而推广的各种Bonferroni平均算子[9-13,24,30,35-36,41-43,53]和Heronian平均算子[14,15,23,37,52]，是两类体现属性间相互作用的集成算子，因此,当属性间存在相互作用时，由它们进行集成决策信息会更加符合决策实际，结果也会更合理。

显然，从Bonferroni平均算子和Heronian平均算子的定义来看，二者并不相同，但是在一定的条件下[11]，Heronian平均算子可以看作Bonferroni平均算子的特殊形式，因此关于二者的各种推广以及决策应用在一定程度上可以相互借鉴。

由于语言多属性决策在经济管理等领域得到了广泛地应用。我们将加权Heronian平均算子以及三参量Heronian平均算子和三参量加权Heronian平均算子推广到语言多属性决策之中，提出了语言加权Heronian平均算子以及三参量语言Heronian平均算子和三参量语言加权Heronian平均算子，并研究了它们的性质。

最后，提出了利用(语言)Heronian平均算子进行多属性决策的方法，并通过两个应用实例说明了方法的可行性。

2 相关概念

定义2.1[8]设ai(i=1,2,…,n)是一组非负数，若：

则称HM为Heronian平均算子。

定义2.2[14]设ai(i=1,2,…,n)是一组非负数，p,q≥0，若：

则称GHM为广义Heronian平均算子。

定义2.3[34,37]设αi=([ai,bi],[ci,di])

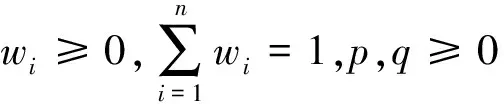
GIIFWHMp,q(a1,a2,…,an)=

则称GIIFWHM为广义区间值直觉模糊加权Heronian平均算子。

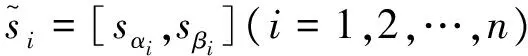
则称GULWHM为广义不确定语言加权Heronian平均算子。

定义2.5[10]设ai(i=1,2,…,n)是一组非负数，p,q,r≥0，若：

则称GBM为广义Bonferroni平均算子。

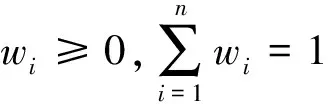
则称GWBM为广义加权Bonferroni平均算子。

定义2.7[56]设S={sα|α=-L,…,L}为语言标度，S中的术语个数为奇数，且满足下列条件：

(1) 若α>β，则sα>sβ；

(2) 存在负算子neg(sα)=s-α。

语言评估标度的运算法则定义如下：

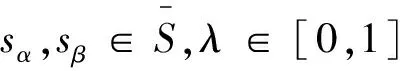
(1)sα+sβ=sα+β；(2)λsα=sλα；

(3)sα×sβ=sαβ； (4) (sα)λ=sαλ。

3 Heronian平均算子

下面给出一种广义加权Heronian平均算子，它不仅具有还原性，而且保持幂等性、单调性以及有界性等性质。

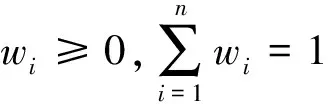
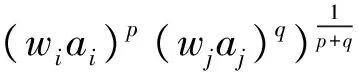
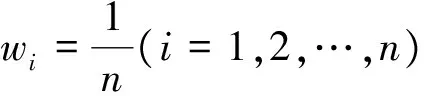
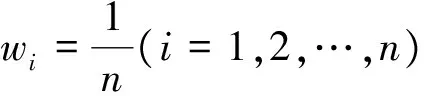
定理3.1 GWHM平均算子具有性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

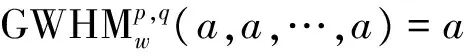
(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)均为非负数，则：

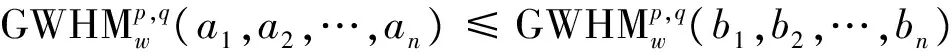
(3)有界性

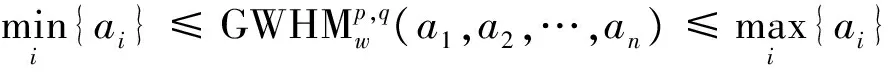
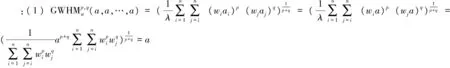
(2) 由ai≤bi(i=1,2,…,n)可知：

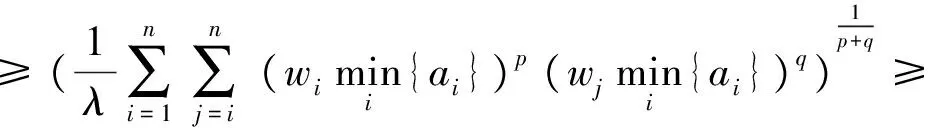
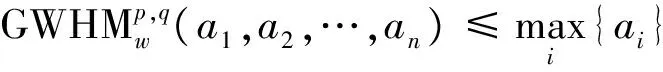
在GBM算子启发下，我们提出：

定义3.2 设ai(i=1,2,…,n)是一组非负数，若

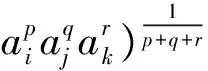
定理3.2 TPHM平均算子有如下性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

TPHMp,q,r(a,a,…,a)=a。

(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)为非负数，则

TPHMp,q,r(a1,a2,…,an)≤TPHMp,q,r(b1,b2,…,bn)。

(3)有界性

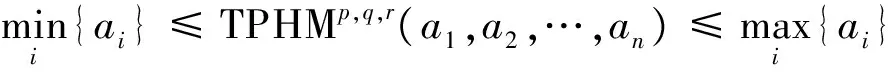
下面给出一种体现属性重要性的三参量加权Heronian平均算子。

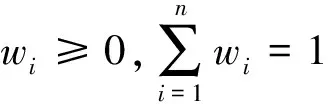
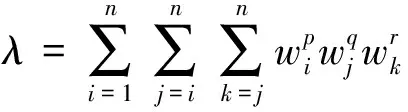
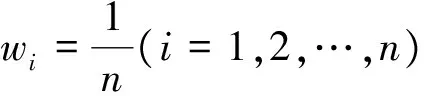
定理3.3 TPWHM平均算子有如下性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

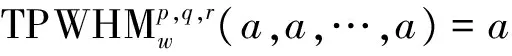
(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)均为非负数，则：

(b1,b2,…,bn)。

(3)有界性

4 语言Heronian平均算子

下面我们将加权Heronian平均算子以及三参量Heronian平均算子和三参量加权Heronian平均算子推广到语言决策之中。首先给出语言Heronian平均算子。

定义4.1 设ai(i=1,2,…,n)是一组语言术语，p,q≥0，若：

则称LHM为语言Heronian平均算子。

定理4.1 设ai=sθi(i=1,2,…,n)是一组语言术语，p,q≥0，则：

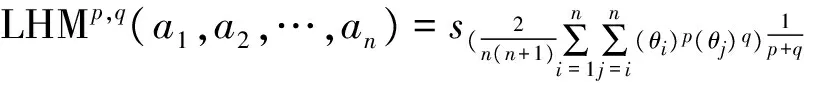
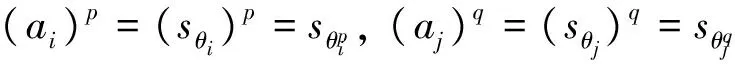
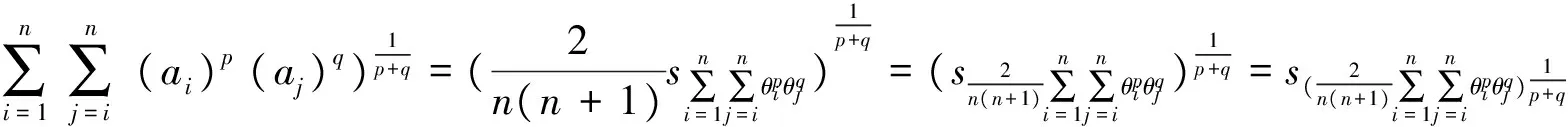
定理4.2 LHM平均算子具有性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

LHMp,q(a,a,…,a)=a。

(2)单调性 若ai≤bi(i=1,2,…,n) ，其中ai,bi(i=1,2,…,n)均为语言术语，则

LHMp,q(a1,a2,…,an)≤LHMp,q(b1,b2,…,bn)。

(3)有界性

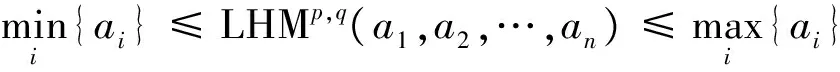
下面给出语言加权Heronian平均算子。

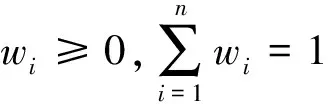
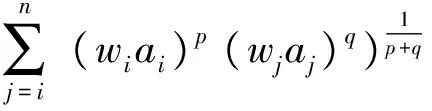
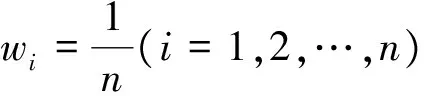
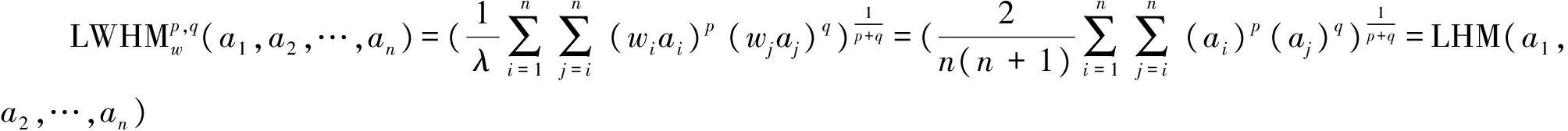
即LWHM算子退化为LHM算子，因此LWHM算子是LHM算子的推广。

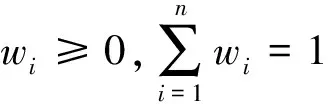
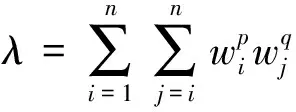
定理4.4 LWHM平均算子具有性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

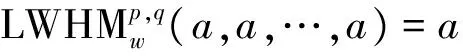
(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)均为语言术语，则：

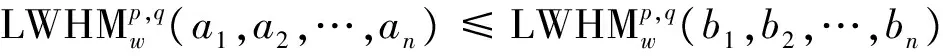
(3)有界性

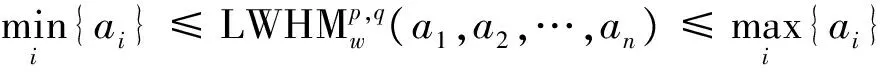
定义4.3 设ai(i=1,2,…,n)是一组语言术语，若：

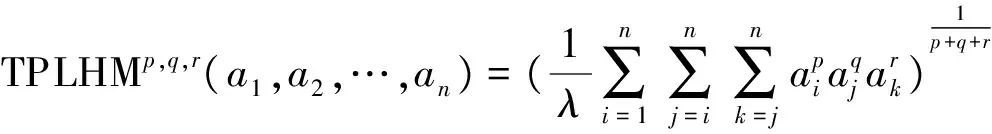
定理4.5 设ai=sθi(i=1,2,…,n)是一组语言术语，则

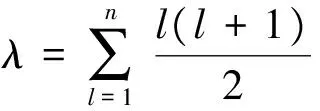
定理4.6 TPLHM平均算子有如下性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

TPLHMp,q,r(a,a,…,a)=a。

(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)为语言术语，则：

TPLHMp,q,r(a1,a2,…,an)≤TPLHMp,q,r(b1,b2,…,bn)。

(3)有界性

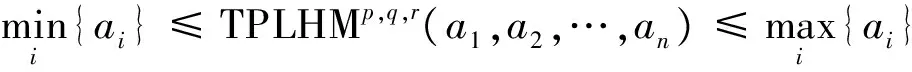
下面定义三参量语言加权Heronian平均算子。

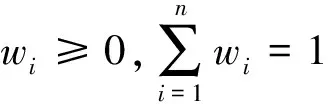
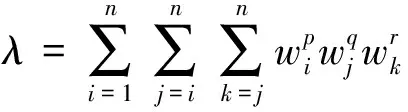
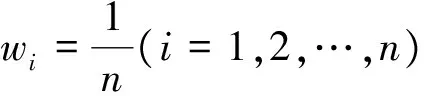
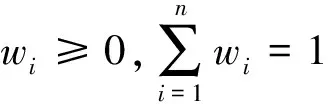
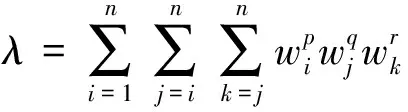
定理4.8TPLWHM平均算子具有性质：

(1)幂等性 若ai=a(i=1,2,…,n)，则：

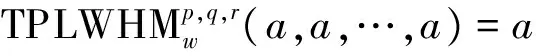
(2)单调性 若ai≤bi(i=1,2,…,n)，其中ai,bi(i=1,2,…,n)均为语言术语，则：

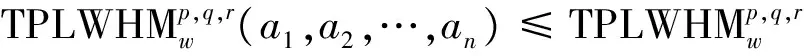
(3)有界性

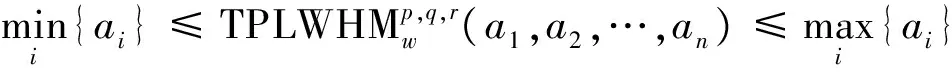
5 决策应用

本节中，我们研究基于(语言)Heronian平均算子的多属性决策方法。首先，分析决策方法的特点及适用范围。然后，给出基于(语言) Heronian平均算子的多属性决策方法。

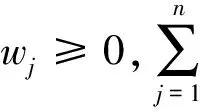
步骤1 决策者给出方案xi关于属性uj的属性值为aij，得到决策矩阵为A=(aij)mn，其中aij(i=1,2,…,m,j=1,2,…,n)为非负实数或语言变量。

步骤2将决策矩阵进行规范化处理，得到规范化决策矩阵R=(rij)mn；若决策矩阵为语言变量决策矩阵，无需进行规范化。

步骤3 根据Heronian平均算子或语言Heronian平均算子，计算各方案综合评价值。

步骤4 根据各方案综合评价值的大小对方案进行排序择优。

例5.1[57]某投资银行对某市4家企业xi(i=1,2,3,4)进行投资，评估指标分别为：产值(u1)、投资成本(u2)、销售额(u3)、国家收益比重(u4)和环境污染程度(u5)。该投资银行考察了上年度4家企业的上述指标情况(其中污染程度由有关环保部门检测并量化)，所得评估结果如表5.1所示。各项评估指标中投资成本和环境污染程度为成本型，其余为效益型。属性权重为w=(0.36,0.16,0.16,0.16,0.16)。试确定最佳投资企业。

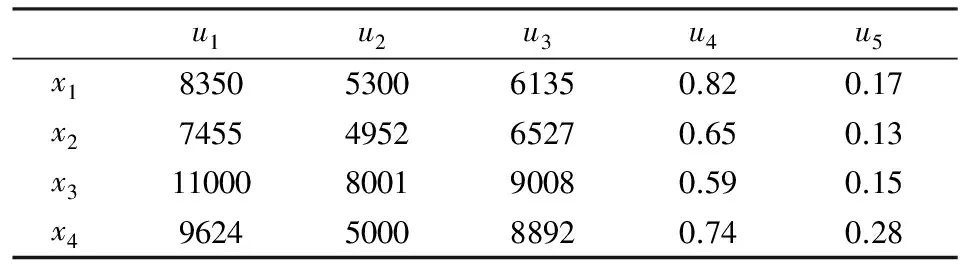
表5.1 决策矩阵

显然, 企业的产值、投资成本、销售额、国家收益比重和环境污染程度之间并非相互独立，而是存在相互作用关系。比如,产值的高低会影响到投资成本和销售额；环境污染程度必然对国家受益比重和投资成本带来影响；类似可以分析每个属性对其他两个属性均有影响。因此，考虑使用本文提出的TPWHM算子进行信息集成。

首先，将原始决策矩阵规范化，得到规范化矩阵为：

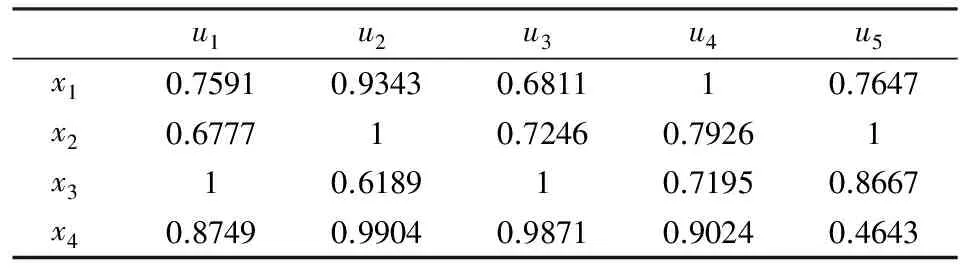
表5.2 规范化决策矩阵

其次，使用TPWHM算子进行集结(不妨取p=q=r=1)，此时：

于是有：

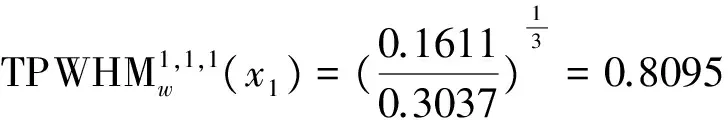
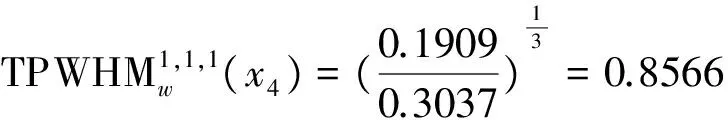
由方案的综合属性值大小可得方案排序为：x3≻x4≻x1≻x2。所以最佳投资企业为x3。

为了与假设属性相互独立的集成算子进行比较，我们分别使用OWA算子、OGW算子和OWH算子对各方案属性值进行集结。

通过OWA算子集成得方案综合属性值为：

z(x1)=0.8623,z(x2)=0.8712,z(x3)=0.8728,z(x4)=0.8731

于是，方案排序为x4≻x3≻x2≻x1,即最佳投资企业为x4。

通过OWG算子集成得方案综合属性值为：

z(x1)=0.8527,z(x2)=0.8599,z(x3)=0.8587,z(x4)=0.8469

故方案排序为x2≻x3≻x1≻x4,于是最佳投资企业为x2。

由OWH算子集成得方案综合属性值为：

z(x1)=0.8430,z(x2)=0.8483,z(x3)=0.8435,z(x4)=0.8128

从而得到方案排序为x2≻x3≻x1≻x4,即最佳投资企业为x2。

比较上述结果发现，使用考虑属性间相互作用的TPWHM算子进行集成，与使用OWA算子、OGW算子和OWH算子进行集成，所得到的排序结果完全不同，这主要是OWA算子、OGW算子和OWH算子在集成信息时假设属性独立，而TPWHM算子考虑到了属性间的相互作用,因此本文决策结果更加符合实际。

例5.2[58]某单位在对干部进行考核选拔时，制定了6项考核指标(属性)：思想品德(u1)、工作态度(u2)、工作作风(u3)、文化水平和知识结构(u4)、领导能力(u5)、开拓能力(u6)，且权重向量为w=(0.22，0.11，0.19，0.10，0.16，0.22)。专家对各候选人按上述6项指标利用语言标度S={s-4=极差,s-3=很差,s-2=差,s-1=稍差,s0=一般,s1=稍好,s2=好,s3=很好,s4=极好}对5位候选人xi(i=1,2,3,4,5)进行评估，并给出语言决策矩阵。试确定最佳候选人。

表5.3 语言变量决策矩阵

由于一个人的思想品德、工作态度、工作作风、文化水平和知识结构以及领导能力和开拓能力不是相互独立的，而是相互影响的，比如，思想品德对工作态度和工作作风产生积极地影响，而工作态度对工作作风和开拓能力具有促进作用，等,类似地可以分析每个属性对其他两个属性均有影响。故可使用本文提出的TPLWHM算子进行信息集成，不妨取p=q=r=1。此时：

于是

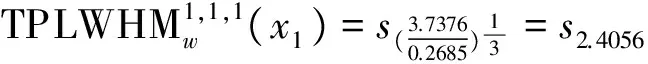
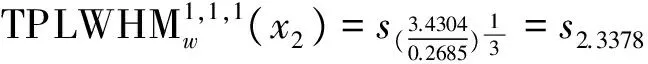
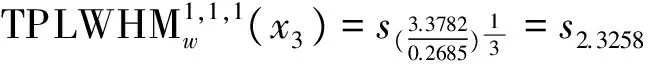
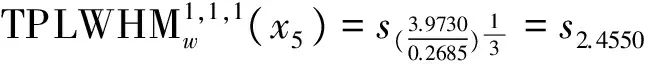
由方案语言综合属性值大小，得到方案优劣排序为：x4≻x5≻x1≻x2≻x3。故最佳候选人为x4。 为了进一步分析TPLWHM算子中参数对集成结果以及方案排序的影响,我们令参数p,q,r取不同数值,然后计算出各方案相应的综合属性值,并将综合属性值和方案排序列入下表(见表5.4)。

由表5.4可以看出，当参数p=1，q,r增加时，方案综合属性值随之递增；而当p=2或p=3时，q,r增加时，方案综合属性值没有出现递增情况。因此，方案综合属性值的变化与参数p,q,r的取值没有明显的规律。

由方案排序结果可见，当参数p=q=r=1时，方案排序为x4≻x5≻x1≻x2≻x3；当参数p,q,r增大时，方案排序变为x4≻x1≻x2≻x5≻x3或x4≻x2≻x1≻x5≻x3，且最优方案一直不变。显然，当参数p,q,r变化时，虽然方案排序发生了变化，但是变化并不大，而且排序结果非常稳定。此外，注意到TPWHM算子中，随着参数p,q,r变大，λ值的逐渐变小，也给计算带来极大的不便。因此，我们建议使用TPWHM算子进行信息集成时，参数p,q,r可以取1，2等较小的数，此时既考虑到了属性之间的相互作用，也使得计算非常简便。

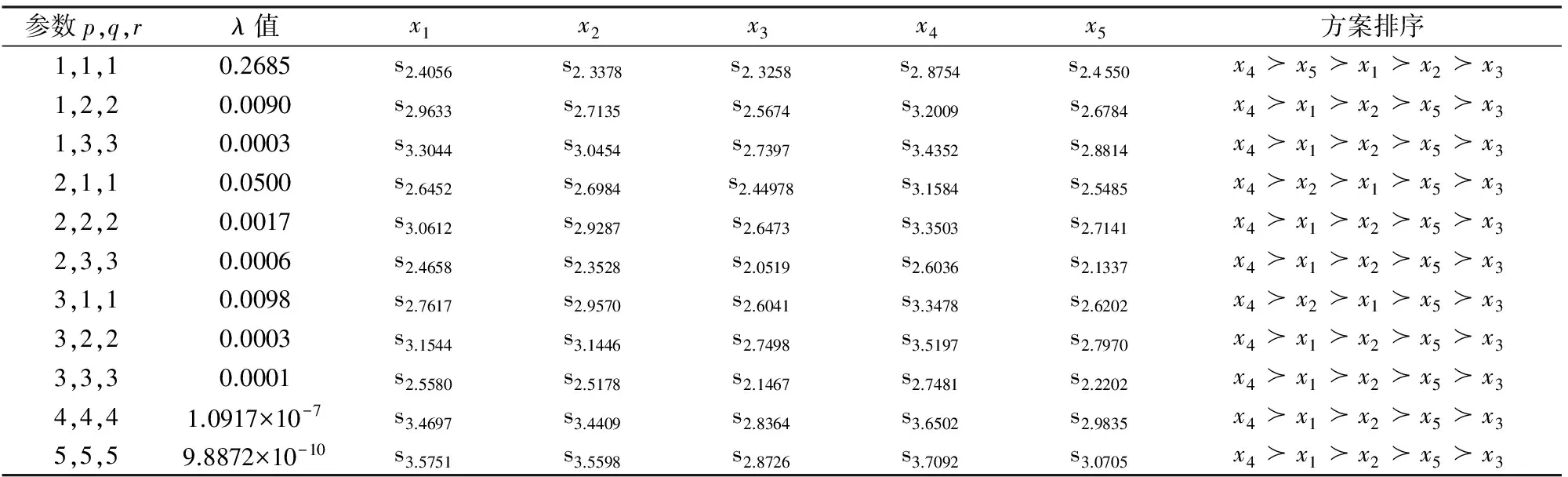
表5.4 不同参数下方案综合属性值及方案排序

6 结语

提出了具有还原性的WHM算子，定义了TPHM算子和TPWHM算子，并研究了它们的性质。然后，定义了LWHM算子，TPLHM算子和TPLWHM算子，并对它们的性质进行了研究。最后，通过两个实例说明了这些算子在多属性决策中的应用。本文研究进一步推广了Heronian平均算子，同时语言Heronian平均算子的提出和应用，也拓展了Heronian平均算子的应用范围。

[1] Harasnyi J C.Cardinal welfare,individualistic ethics,and interpersonal comparisons of utility[J]. Journal of Political Economy,1955,63(4):309-321.

[2] Aczel J, Alsina C. Synthesizing judgement: A functional equation approach[J]. Mathematical Modelling, 1987,9(3-5): 311-320.

[3] Yager R R. On ordered weighted averaging aggregation operators in multicriteria decision making[J]. IEEE Transactions on Systems, Man, and Cybernetics,1988, 18(1):183-190.

[4] Herrera F, Herrera Viedma, Chiclana F. Multiperson decision-making based on multiplicative preference relations[J]. European Journal of Operational Research, 2001,129(2):372-385.

[5] 陈华友,刘春林,盛昭瀚. IOWHA算子及其在组合预测中的应用[J].中国管理科学,2004,12(5):35-40.

[6] Fodor J, Marichal J L, Roubens M. Characterization of the ordered weighted averaging operators[J]. IEEE Transactions on Fuzzy Systems, 1995, 3(2): 236-240.

[7] Bonferroni C. Sulle medie multiple di potenze[J]. Bolletino Matematica Italiana,1950,5(3):267-270.

[8] Beliakov G,Pradera A, Calvo T. Aggregation functions: A guide for practitioners[M]. Berlin: Springer,2007.

[9] Yager R R.On generalized Bonferroni mean operators for multi-criteria aggregation[J]. International Journal of Approximate Reasoning, 2009,50(8):1279-1286.

[10] Beliakov G, James S, Mordelva J,et al. Generalized Bonferroni mean operators in multi-criteria aggregation[J]. Fuzzy Sets and Systems,2010,161(17): 2227-2242.

[11] Xia Meimei, Xu Zeshui, Zhu Bin. Generalized intuitionistic fuzzy Bonferroni means[J]. International Journal of Intelligent Systems,2012, 27(1):23-47.

[12] Zhou Wei, He Jianmin. Intuitionistic fuzzy geometric Bonferroni means and their application in multicriteria decision making[J]. International Journal of Intelligent Systems,2012,27(12):995-1019.

[13] Xia Meimei, Xu Zeshui, Zhu Bin. Geometric Bonferroni means with their application in multi-criteria decision making[J]. Knowledge-Based Systems, 2013,40:88- 100.

[14] 刘焕章,裴道武.H-OWA算子及其在多属性决策中的应用[J].浙江理工大学学报.2012,29(1): 138-142.

[15] Yu Dejian. Intuitionistic fuzzy geometric Heronian mean aggregation operators[J]. Applied Soft Computing, 2013,13(2):1235-1246.

[16] Xu Zeshui，Da Qingli.The uncertain OWA operator[J]. International Journal of Intelligent Systems,2002,17(6): 569-575.

[17] Xu Zeshui,Da Qingli.An uncertain ordered weighted geometric(UOWG) operator and its application[J]. Information,2004,7(2): 175-182.

[18] Yager R R. OWA aggregation over a continuous interval argument with applications to decision making[J].IEEE Transactions on Systems, Man, and Cybernetics,Part B:Cybernetics,2004,34(5):1952-1963.

[19] Yager R R, Xu Zeshui. The continuous ordered weighted geometric operator and its application to decision making[J].Fuzzy Sets and Systems,2006,157(10): 1393-1402.

[20] 徐泽水.拓展的C-OWA算子及其在不确定多属性决策中的应用[J].系统工程理论与实践，2005,25(11): 7-13.

[21] 刘小弟，朱建军，刘思峰.方案有不确定偏好的区间数相对熵群决策方法[J].中国管理科学,2014,22(6): 134-140.

[22] 刘健,刘思峰.属性值为区间数的多属性决策对象排序研究[J].中国管理科学, 2010,18(3):90-94.

[23] 王东晓,李自强,刘卫锋.区间数Heronian平均算子[J].数学的实践与认识,2015,45(21):274-281.

[24] Xu Zeshui. Uncertain Bonferroni mean operators[J]. International Journal of Computational Intelligence Systems,2010,3(6):761-769.

[25] Bellman R E,Zadeh L A.Decision-making in a fuzzy environment[J]. Management Science,1970,17(4): B141- B164.

[26] 徐泽水.基于FOWA算子的三角模糊数互补判断矩阵排序法[J].系统工程理论与实践,2003,23(10)：86-89.

[27] 王欣荣，樊治平.一种有序加权(FOWA)算子及其应用[J].模糊系统与数学,2003,17(4):67-72.

[28] 徐泽水.一种FOWG算子及其在模糊AHP中的应用[J].系统工程与电子技术,2002,24(7):31-33.

[29] 许叶军，达庆利.TFOWA算子及其在决策中的应用[J].东南大学学报(自然科学版),2006,36(6): 1034- 1038.

[30] 刘金培,林盛,陈华友.模糊Bonferroni平均算子及在多准则群决策中的应用[J].系统工程与电子技术, 2012,34(1):115-119.

[31] Xu Zeshui. Intuitionistic preference realtions and their application in group decision making[J].Information Science,2007,177(11):2363-2379.

[32] Xu Zeshui. Intuitionistic fuzzy aggregation operator[J]. IEEE Transactios on Fuzzy Systems,2007,15(6):1179- 1187.

[33] Xu Zeshui, Yager R R. Some geometric aggragation operators based on intuitionistic fuzzy sets[J]. International Journal of General System,2006,35(4): 417-433.

[34] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219.

[35] Xu Zeshui, Yager R R. Intuitionistic fuzzy Bonferroni means[J].IEEE Transactions on Systems,Man and, Cybernetics- Part B: Cybernetics,2011,41(2):568-578.

[36] Xu Zeshui, Chen Qi. A multi-criteria decision making procedure based on interval-valued intuitionistic fuzzy Bonferroni means[J].Journal of Systems Science and Systmes Engineering,2011,20(2): 217-228.

[37] Yu Dejian, Wu Yingyu. Interval-valued intuitionistic fuzzy Heronian mean operators and their application in multi-criteria decision making[J].African Journal of Business Management. 2012,6(11):4158-4168.

[38] Torra V. Hesitant fuzzy sets[J]. International Journal of Intelligent Systems,2012,25(6):529-539.

[39] Zhang Zhiming. Hesitant fuzzy power aggregaton operators and their application to multiple group decision making[J]. Information Science,2013,234: 150-181.

[40] Wang Weize, Liu Xinwang. Some hesitant fuzzy geometric operators and their application to multiple attribute group decision making[J]. Technological and Economic Development of Economy,2014,20(3): 371-390.

[41] Zhu Bin，Xu Zeshui, Xia Meimei. Hesitant fuzzy geometric Bonferroni means[J]. Information Sciences,2012,205: 72-85.

[42] Yu Dejian, Wu Yingyu, Zhou Wei. Generalized hesitant fuzzy Bonferroni mean and its application in multi-criteria group decision making[J]. Journal of Information and Computational Science,2012,9(2):267-274.

[43] Zhu Bin，Xu Zeshui. Hesitant fuzzy Bonferroni means for multi-criteria decision making[J]. Journal of the Operational Research Society,2013,64(12):1831-1840.

[44] Bedregal B, Reiser R, Bustince H, et al. Aggregation functions for typical hesitant fuzzy elements and the action of automorphisms[J]. Information Sciences, 2014,255:82-99.

[45] Bordogna G, Fedrizzi M, Passi G. A linguistic modeling of consensus in group decision making on OWA operator[J]. IEEE Transactions on Systems, Man, and Cybernetics,Part A:Systems and Humans,1997,27(1):126-132.

[46] 戴跃强,徐泽水,李琰,等.语言信息评估新标度及其应用[J].中国管理科学,2008,16(2): 145- 149.

[47] Xu Zeshui. EOWA and EOWG operators for aggregating linguistic labels based on linguistic preference relations[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems,2004,12(6): 791-810.

[48] Torra V. The weighted OWA operator[J]. International Journal of Intelligent Systems, 1997, 12(2): 153-166.

[49] Xu Zeshui. On generalized induced linguistic aggregation operators[J]. International Journal of General Systems, 2006,35(1):17-28.

[50] Xu Zeshui. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment[J]. Information Sciences,2004,168(1-4):171-184.

[51] Xu Zeshui. Induced uncertain linguistic OWA operators applied to group decision making[J]. Information Fusion,2006,7(2):231-238.

[52] Liu Xiaodi, Zhu Jianjun,Liu Guoding, et al. A multiple attribute decision making method based on uncertain linguistic Heronian mean[J]. Mathematics Problems in Engineering, 2013,2013:1-11.

[53] 刘金培,林盛,陈华友. 二元语义Bonferroni集成算子及在多属性决策中的应用[J].运筹与管理,2013, 22 (5):122-127.

[54]彭勃,叶春明.基于不确定纯语言混合调和平均算子的多属性群决策方法[J]. 中国管理科学,2015,23(2): 131-138.

[55] 王坚强,吴建文.基于区间灰色不确定语言的多准则决策方法[J].中国管理科学,2010,18(3):107-111.

[56] Liu Peide, Liu Zhengmin, Zhang Xin. Some intuitionistic uncertain linguistic Heronian mean operators and their application to group decision making[J]. Applied Mathematics and Computation,2014,230: 570-586.

[57] 刘家学.带有方案偏好信息的多指标决策法[J].系统工程与电子技术,1999,21(1):4-7.

[58] 徐泽水.语言多属性决策的目标规划模型[J].管理科学学报,2006,9(2):9-17.

(Linguistic) Heronian Mean Operators andApplications in Decision Making

LIU Wei-feng, CHANG Juan, DU Ying-xue

(School of Science, Zhengzhou University of Aeronautics,Zhengzhou 450015, China)

In information aggregation of multiple attribute decision making, some aggregation operators are defined based on the hypothesis in which all the attributes are mutually indenpent, resulting in unreasonable information aggregation and decision result. Heronian mean operator is an aggregation opeator in which can deal with the situation of interrelationshiop between attributes, and from the theoretical and and practical points of view, it is worth to study and generalize Heronian mean operator. Firstly, aiming at weighted Heronian mean operator without reducibility in related reference, the generalized weighted Heronian mean operator(GWHM) with reducibility is introduced. And then, the three parameters Heronian mean operator(TPHM) and the three parameters weighted Heronian mean operator(TPWHM) are defined, and their basic properties such as idempotency, monotonicity and boundness are studied. Further, in order to fulfill applications of Heronian mean operator in linguistic multiple attribute decision making, linguistic weighted Heronian mean operator(LWHM), three parameters linguisitic Heronian mean operator(TPLWHM) and three parameters linguisitic weighted Heronian mean operator(TPLHM) are dedined, and their properties such as idempotency, monotonicity and boundness are also discussed. Finally, an approach to multiple attribute decision making based on the (linguisitic) Heronian mean operators is proposed, and two practical examples are given to illustrate our results.

aggregation operator; Heronian mean operator; linguistic Heronian mean operator; decision making

2015-06-16；

2016-02-02

国家自然科学基金资助项目(11501525)；郑州航空工业管理学院青年科研基金(2016113001)

刘卫锋(1976-)，男(汉族)，河南沈丘人，郑州航空工业管理学院数理系，副教授，研究方向:数学建模、模糊数学，E-mail:lwf0519@163.com.

1003-207(2017)04-0174-10

10.16381/j.cnki.issn1003-207x.2017.04.021

C934

A