分销供应链中零售商横向竞争下采购联盟的稳定结构

肖 旦，周永务，史欣向，李昌文

(1. 广州大学工商管理学院，广东 广州 510006; 2.华南理工大学工商管理学院，广东 广州 510640;3.中山大学粤港澳发展研究院，广东 广州 510275; 4.淮北师范大学信息学院，安徽 淮北 235000)



分销供应链中零售商横向竞争下采购联盟的稳定结构

肖 旦1，周永务2，史欣向3，李昌文4

(1. 广州大学工商管理学院，广东 广州 510006; 2.华南理工大学工商管理学院，广东 广州 510640;3.中山大学粤港澳发展研究院，广东 广州 510275; 4.淮北师范大学信息学院，安徽 淮北 235000)

本文针对由单一供应商和三个横向竞争零售商所组成的两层分销供应链系统，采用合作博弈论中描述远视参与者的最大一致集(LCS)概念，在供应商所提供的不同契约形式下，分别研究了横向竞争零售商采购联盟的远视稳定结构。研究发现，当供应商提供线性折扣契约时，根据供应商提供的折扣比例不同，横向竞争零售商的采购联盟结构是不同的，当折扣比例较低(小于0.5)时，横向竞争的零售商会形成仅两个零售商联合采购的联盟结构，将第三个零售商排除在联盟之外；而当折扣比例较高(大于0.5)时，横向竞争的远视零售商将只会形成大联盟，以增强共同的竞争力。但是，当供应商提供两部收费制折扣契约时，无论供应商所提供的折扣比例如何变化，横向竞争零售商都以三个零售商联合采购的大联盟为稳定结构。此外，通过数值例子发现，供应商提供其他形式的数量折扣契约时，横向竞争的远视零售商会以大联盟为稳定结构。

分销供应链；合作博弈论；采购联盟；远视零售商

1 引言

采购在企业的实际运作中扮演着非常重要的作用。近十年来，随着科技的高速发展和企业管理水平的不断提升，许多新的采购模式应运而生，例如，信息采购、定制采购和联合采购等，其中，联合采购吸引了企业界和学术界的广泛关注。联合采购指同一行业间多家机构或组织，将需要采购的产品数量进行汇集，向供应商统一采购的行为。联合采购可以增强讨价还价的能力，降低采购成本，带来盈余。采购联盟则是将联合采购所带来的盈余进行公平合理分配所形成的稳定组织，如成立于1990年的美国最大联合采购组织FPN(Federation of Pharmacy Networks药业网络联合会)，在全美国总共拥有22个药品联合采购集团，代表1万4千多家独立药店进行联合采购。

许多采购联盟虽然在采购领域进行了合作，但是在其他领域却依然保持着适度的竞争关系。1996年，Brandenburger和Nalebuff[1]在《合作竞争》一书中曾指出：“经济市场既不是一个完全竞争的市场，也不是一个完全合作的市场，而是一个既有竞争又有合作的市场。”Hendrick[2]通过调研指出虽然有60%的采购联盟存在于非竞争者之间，而仍然有10%的联盟是由竞争者所构成的。例如，相纸采购联盟Photo Fair Stores的成员主要是位于美国新泽西州北部的小型相片冲印商，他们之间存在着明显的竞争关系，但他们加入采购联盟形成长期的合作关系之后，每个成员的利润都可以得到增加，即“帮助竞争者对自己也有益”。目前关于采购联盟的理论研究以定性为主，只有少量学者进行了定量地分析[3-5]，并且他们假设采购联盟成员之间相互独立，没有直接的竞争关系。而本文针对实际中广泛存在的横向竞争零售商进行联合采购的情形，采用合作博弈论中远视稳定性的概念，对零售商所形成采购联盟的远视稳定结构进行理论分析。

与本文相关的文献主要包括以下两个方面：数量折扣契约在供应链中的应用和供应链联盟的稳定性。首先，许多学者认识到数量折扣契约是上游供应商或制造商促使供应链协调、改善供应链整体绩效的十分有效的激励机制之一，并对此进行了充分的讨论[6-8]。但是，他们并没有分析数量折扣契约对下游零售商联合采购决策的影响。随后，一些学者在下游有两个零售商存在的情况下，对零售商进行联合采购时的运作策略展开了初步研究。如，刘斌等[9]在应急采购情形下分析了短生命周期产品的联合采购策略，陈敬贤等[10]以包含一个供应商和两个零售商的分销渠道为研究对象，研究了团购策略对于渠道绩效的影响，刘春玲等[11]则讨论了基于Credit期权的集群式供应链联合采购模型。但是，他们都没有考虑多个(两个以上)零售商形成联合采购联盟时，数量折扣契约对采购联盟运作策略及稳定性的影响。目前，对于供应链中合作联盟稳定性的讨论，主要可分为短视参与者联盟的稳定性和远视参与者联盟的稳定性(或稳定结构)两类。本文所刻画的短视参与者是指他们不会考虑到自己从联盟中“叛逃”的行为会引起未来进一步“叛逃”联盟行为的发生；而远视参与者则恰好相反，现在大多数的研究则集中于对短视参与者合作联盟稳定性的讨论[12-14]。但是，随着博弈论成果的不断丰富，已有许多学者开始借鉴新出现的远视合作博弈解概念，对供应链中具有远视参与者的合作联盟的稳定结构进行了讨论。国外学者首先对组装供应链系统中远视供应商联盟的稳定结构进行了一系列的探讨[15-17]，随后，国内学者郑士源和王浣尘[18]利用合作博弈中最大一致集的方法对航空企业的竞争和联盟进行了研究，曾银莲等[19]也采用此方法分析了合作运输联盟结构的稳定性，但是他们都没有考虑供应链成员之间的相互竞争性。此后，Granot和Sosic[20]与Nagarajan和Sosic[21]讨论了相互竞争的远视参与者形成联盟的稳定结构；国内学者周永务等[22]也利用最大一致集的概念分析了供应商对不同零售商定价联盟结构的稳定性。然而，他们没有考虑到上游供应商所提供的数量折扣契约对相互竞争零售商所形成联盟结构的影响。

本文将针对由一个供应商与三个基于Cournot竞争的零售商组成的两层分销供应链系统，在不同形式的数量折扣契约下，分别研究远视零售商联盟的稳定结构。重点考察不同的数量折扣契约形式对零售商采购联盟稳定性的影响，旨在为分销供应链系统中的零售商提供合理且可操作的结盟建议。

2 模型假设与记号

考虑一个两层的分销供应链系统，上游一个供应商向下游三个相互竞争的零售商提供同质产品，且单位产品的批发价格与其所收到订单信息中的采购量成反比。下游三个零售商在进行联合采购时可以形成三种不同的联盟结构，分别是各自独立采购(I)、两个零售商的联合采购(M)以及三个零售商的联合采购(G)，如图1所示。

图1 横向竞争零售商的三种采购联盟结构

竞争关系的描述：

假定供应商记为S，三个相互竞争零售商的集合记为N={1, 2, 3}。下游的三个零售商同时独立确定各自的采购量，设零售商i∈N的采购量为qi≥0，向量q={q1,q2,q3}为三个零售商采购量的一个组合，则零售市场中产品的总量为Q=q1+q2+q3。如果零售市场上产品的供给和需求达到均衡，则产品以市场出清价格进行销售，不妨设产品的出清价格P与下游零售商的总订货量为线性关系，即，P=A-Q(Ha和Tong[23]，不考虑竞争强度对采购联盟结构的影响)。此时，三个零售商之间为Cournot竞争关系，零售商i的销售收益Ri(q)不仅与自身的订货量qi有关，而且还与其他零售商的订货量qj(j≠i)有关。从而，零售商i的收益Ri(q)为：Ri(q)=qi(A-Q)，其中，A为下游三个零售商的最大总订货量。

合作关系的描述：

在实际采购活动中，如果零售商的采购量越高，则供应商所提供的单位批发价格将越低。而每个零售商的采购能力有限，因此，下游零售商可以采用汇集各方采购量的方式进行联合采购，以降低各方的采购成本。Schotanus等[24]通过实证研究，提出了如下的数量折扣函数w(q)，以刻画实际中可能用到的不同折扣契约形式，w(q)=a+d/qe，其中，a表示产品的基本价格；d表示折扣比例，如果|d|越大，则表示供应商提供的折扣契约对下游零售商的需求聚集效应越高；e表示陡度(Steepness)，特别地，如果e=1，从而，w(q)=a+d/q，则称供应商向零售商提供的批发价格契约是两部收费制折扣契约(Two-part tariff)；如果e=-1，从而，w(q)=a+dq(其中，d<0)，则称供应商向零售商提供的批发价格契约是线性折扣契约(Linearschedule)。Schotanus等[24]指出当e的取值范围在-1到1.6之间时，此数量折扣函数可以拟合实际中常见的66种折扣契约形式，因此，本文主要对以上两种折扣契约进行了讨论，对其他参数组合的情况则用数值例子进行了说明。

3 不同联盟结构下零售商的订货决策

本小节在三个零售商独立采购、两个零售商形成采购联盟以及三个零售商形成采购联盟三种不同的联盟结构下，分别讨论下游零售商的最优订货量，并比较在不同的联盟结构下供应链中各成员的利润关系。

3.1 三个零售商独立订货(I)

如果三个零售商之间没有形成任何采购联盟，并且三个零售商同时选择订货量(订货量不会为负数，下同)作为其博弈策略展开Cournot竞争，则有：

(1)

可得均衡时零售商i的最优订货量满足如下的一阶条件：

(2)

3.2 两个零售商的采购联盟(M)

不妨设零售商1和零售商2形成采购联盟，即将两者的需求进行汇集向上游供应商统一采购，但是零售商1、2和3仍保持着Cournot竞争关系，故：

(3)

(4)

(5)

可得均衡时零售商1、2和3的最优订货量满足如下的一阶条件：

(6)

(7)

(8)

3.3 三个零售商的采购联盟(G)

此时零售商1、2和3形成的采购联盟汇集了各零售商的需求，但是零售商1、2和3仍进行Cournot竞争，故：

(9)

可得均衡时零售商i(i=1, 2, 3)的最优订货量满足如下的一阶条件：

(10)

由于(2)式、(6)式～(8)式和(10)式仅在e=-1和e=1下，即线性折扣契约和两部收费制折扣契约处有显示解存在。因此，本文主要在e=-1，d<0和e=1，d>0两种特殊的情形下，得到显示均衡解，并将相关的结果分别整理于表1和表2中；此外，对于d不变，参数e从0.1变化到1和e从-1变化到-0.1的两种情形，零售商在不同联盟结构中的最优利润分别总结在表3和表4中。

3.4 不同联盟结构下的比较

本小节主要针对供应商可能的数量折扣契约形式(以线性折扣契约和两部收费制折扣契约为主)，在不同联盟结构下，分别讨论了供应链中零售商间的利润关系。

(1)线性折扣契约l

性质1. 供应商提供线性折扣契约时，在三种不同联盟结构下，三个零售商的利润具有如下的关系：

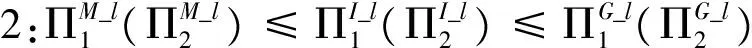
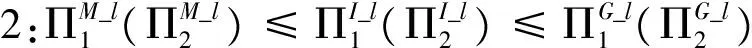
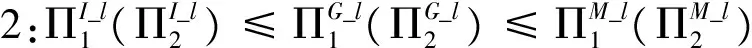
表1 线性折扣契约下(e=-1, d<0)的均衡解

注： -1a.

表2 两部收费制折扣契约下(e=1, d>0)的均衡解

注：d>0，A>a且(A-a)2>16d.

表3 当d=10, e=0.1～1时，零售商在不同联盟结构下的最优利润

表4 当d=-0.3，e=-1～-0.1时，零售商在不同联盟结构下的最优利润

性质1说明，在线性折扣契约下，(1)如果供应商提供的折扣比例很高时(即，d∈(-1, -2/3])，零售商1和2的利润关系与d∈[-2/3, -1/2]是一致的，但是，零售商3在仅零售商1和2结盟的联盟结构中利润最高，在大联盟中的利润次之，而在各自独立订货的联盟结构中最低；(2)如果供应商提供的折扣比例较高时(即，d∈[-2/3, -1/2])，三个零售商均在大联盟(即，三个零售商的采购联盟)中利润达到最高，零售商1和2在二者联合采购之后的利润比三个零售商独立订货时的利润要低，但是，零售商3在零售商1和2形成采购联盟之后的利润比三个零售商互不结盟时的利润高；(3)如果供应商提供的折扣比例较低(即，d∈[-1/2, 0])，零售商1和2在仅由他们二者联合采购形成的联盟结构中利润最高，而零售商3则在大联盟中的利润最高。

这是因为(1)如果供应商提供的折扣比例较低，零售商1和2加入大联盟使得订货成本降低的正效应，低于由于总订货量上升而使产品出清价格降低的负效应，因此，零售商1和2在大采购联盟中的利润比在仅由他们二者联合采购时的利润低，而零售商3的利润则相反；(2)如果供应商提供较高的折扣比例，由于零售商1、2和3在大联盟中订货成本降低带来的正效应，都高于由于总订货量上升使产品出清价格降低的负效应；(3)如果供应商提供的折扣比例很高，则零售商3加入大联盟虽然订货量增加，但是，却导致了零售市场上的竞争更加激烈，使得订货成本降低所带来的正效应，低于产品出清价格降低带来的负效应，因此零售商3在大联盟中的利润较低，而零售商1和2则相反。

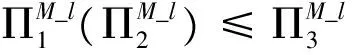
性质2说明，在线性折扣契约下，当供应商提供线性折扣契约时，在零售商1和零售商2联合采购的联盟结构中，如果供应商提供的折扣比例较高(即，d∈(-1, -1/2])，则联盟内零售商的利润要低于联盟外零售商的利润；如果供应商提供的折扣比例较低(即，d∈[-1/2, 0])，则联盟内零售商的利润要高于联盟外零售商的利润。

(2)两部收费制折扣契约t

由于仅零售商1和2形成采购联盟时，零售商1、2和3进行Cournot竞争存在两组不同的Nash均衡解，本小节将对这两种情况分别进行讨论。首先，如果零售商1、2和3进行Cournot竞争的Nash均衡解为M3，则与上面的讨论类似可以得到如下的性质3。

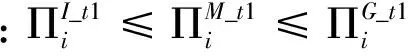
性质3说明，供应商提供两部收费制折扣契约时，如果两个零售商的采购联盟的均衡解为M3，无论供应商提供的折扣比例如何，三个零售商都在大联盟中的利润最高，在两个零售商结盟的利润次之，而在各自独立订货的联盟结构中最少。

其次，如果零售商1、2和3进行Cournot竞争的Nash均衡解为M4，则与上面的讨论类似可以得到如下的性质4。

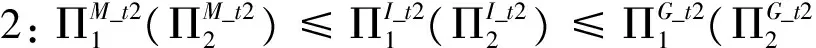
性质4说明，供应商提供两部收费制折扣契约时，如果两个零售商的采购联盟的均衡解为M4，当零售商1和2结盟时，则零售商1和2各自的利润将会最低，而在大联盟中他们的利润达到最高，则独立订货时的利润则介于两者之间。而对于零售商3，则在仅零售商1和2结盟时的利润最高，而大联盟的利润次之，在各自独立订货时的利润最低。

(3)其他契约情形下

如果供应商提供的契约形式是d=10,e=0.1～1和d=-0.3，e=-1～-0.1两组参数，则与上面的讨论类似可以得到如下的性质5～性质6。

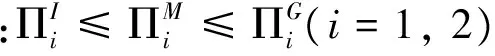
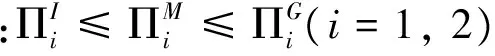
4 联盟的稳定结构

4.1 远视稳定性的概念

本小节将采用Chwe[25]所提出的最大一致集(Largest Consistent Set, LCS)概念，对远视参与者联盟的稳定结构进行刻画,下面将对本节所用到的几个概念给出定义。

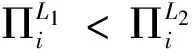
定义2. 联盟结构的直接占优[18, 22, 25]：(1)对于一个成员的子集S，如果对于∀i∈S，都有L1iL2成立，则记为L1SL2，说明成员集合S中的成员都更偏好于联盟结构L2。(2)如果S中的所有成员从联盟结构L1叛逃使得联盟结构变成L2，则记为L1→SL2。(3)如果存在成员集合S，使得L1→SL2并且L1SL2，则称联盟结构L1被联盟结构L2直接占优，记为L1

定义3. 联盟结构的间接占优[18, 22, 25]：如果存在m个联盟结构L1，L2，…，Lm和m个成员集合S1，S2，…，Sm，使得Li→SiLi+1且LiSiLm，i=1,2,…,m-1，则称联盟结构L1被联盟结构Lm间接占优，记为L1<

定义4. 联盟结构集合的一致性[18, 22, 25]：一个由联盟结构组成的集合Y被称为一致集，如果对于Y中的任意一种联盟结构L当且仅当对所有的联盟结构V和联盟S，L→SV，存在联盟结构B∈Y使得V=B或V≪B且L/SB。

4.2 零售商对联盟结构的偏好顺序

本节将在不同情形下，分别讨论零售商对联盟结构的偏好顺序，首先根据性质1和性质2，可知供应商提供线性折扣契约时，有如下性质7成立。

性质7. 如果供应商提供线性折扣契约，则三个零售商对联盟结构的偏好顺序如下：

(1)当d∈(-1, -2/3]时，

{(12), 3}～1{(13), 2}1{1, 2, 3}1{(123)}1{(23), 1}

{(12), 3}～2{(23), 1}2{1, 2, 3}2{(123)}2{(13), 2}

{(13), 2}～3{(23), 1}3{1, 2, 3}3{(123)}3{(12), 3}

(2)当d∈[-2/3, -1/2]时，

{(12), 3}～1{(13), 2}1{1, 2, 3}1{(23), 1}1{(123)}

{(12), 3}～2{(23), 1}2{1, 2, 3}2{(13), 2}2{(123)}

{(13), 2}～3{(23), 1}3{1, 2, 3}3{(12), 3}3{(123)}

(3)当d∈[-1/2, 0]时，

其次，根据性质3可知，如果供应商提供两部收费制折扣契约，且两个零售商的采购联盟下的均衡解为M3，有如下性质8成立。

性质8. 如果供应商提供两部收费制折扣契约，且两个零售商的采购联盟下的均衡解为M3，则三个零售商对联盟结构的偏好顺序如下：

然后，根据性质4，可知如果供应商提供两部收费制折扣契约，且两个零售商的采购联盟下的均衡解为M4，有如下性质9成立。

性质9. 如果供应商提供两部收费制折扣契约，且两个零售商的采购联盟下的均衡解为M4，则三个零售商对联盟结构的偏好顺序如下：

{(12), 3}～1{(13), 2}1{1, 2, 3}1{(123)}1{(23), 1}

{(12), 3}～2{(23), 1}2{1, 2, 3}2{(123)}2{(13), 2}

{(13), 2}～3{(23), 1}3{1, 2, 3}3{(123)}3{(12), 3}

4.3 竞争型零售商采购联盟的稳定结构

本节根据零售商对联盟结构的偏好，分析零售商横向竞争下采购联盟在远视意义下的稳定结构，得到了如下的定理1和定理2。

定理1. 如果供应商提供线性折扣契约，则当d∈(-1, -1/2]时，分销供应链中零售商横向竞争下采购联盟的远视稳定结构为G∈LCS；当d∈[-1/2, 0]时，分销供应链中零售商横向竞争下采购联盟的远视稳定结构为M，即M∈LCS。

证明：如果d∈[-1/2, 0]。则当联盟结构为L=I={1, 2, 3}时，假设零售商1和2从该联盟结构中“叛逃”出去，形成联盟结构V=M={(12), 3}，即，L={1, 2, 3}⇀1, 2{(12), 3}=V。因为{1, 2, 3}1, 2{(12), 3}，所以，当且仅当我们能找到一种联盟结构B≠{(12), 3}，使得{(12), 3}≪B并且{1, 2, 3}/1, 2B时，I={1, 2, 3}∈LCS。由于{(123)}1, 2{(12), 3}，从而，B不可能是{(123)}，此外，由于任意的零售商或零售商联盟从{(12), 3}中“叛逃”出来，必定包含零售商1或2，从而B={1, 2, 3}、{(13), 2}或者{(23), 1}都不能满足{(12), 3}≪B。因此，I∉LCS。

当联盟结构为L=G={(123)}时，假设零售商2和3从大联盟G中“叛逃”出去，形成联盟结构{(23), 1}，即，L={(123)} ⇀2, 3{(23), 1}=V。由于{1, 2, 3}1, 2, 3{(123)}和{(123)}2, 3{(23), 1}，因此，当且仅当我们能找到一个联盟结构B≠{1, 2, 3}和{(23), 1}，使得{(23), 1}≪B并且{(123)};1<2, 3B时，{(123)}∈LCS。与上面的讨论相似，可知{(123)}，{(12), 3} 和{(13), 2}都不能使得{(23), 1}≪B成立。因此，G∉LCS。

当联盟结构为L=M时，不妨假设为{(12), 3}，考虑如下几种情形：(a)零售商1“叛逃”形成联盟结构{1, 2, 3}将不会发生；(b)零售商1和3结盟“叛逃”形成联盟结构{(13), 2}，即{(12), 3}⇀1, 3{(13), 2}，将会被B=V={(13), 2}所阻止，其他的两个零售商的联合“叛逃”也将被阻止； (c)所有零售商“叛逃”形成大联盟G，V={(123)}，将被随后的一系列“叛逃”所阻止，即，{(12), 3}⇀1, 2, 3{(123)} ⇀1, 2{(12), 3}，而{(12), 3}1, 2, 3{(12), 3}，{(123)} ⇀1, 2{(12), 3}，{(123)}1, 2{(12), 3}。因此，M∈LCS。

与以上的证明相似，可以知道当d∈(-1, -1/2]时，G∈LCS。

因此，综上可知，当d∈(-1, -1/2]时，分销供应链中零售商横向竞争下采购联盟的远视稳定结构为G∈LCS；当d∈[-1/2, 0]时，分销供应链中零售商横向竞争下采购联盟的远视稳定结构为M，即M∈LCS。证毕。#

与定理1的证明类似，在供应商提供两部收费制折扣契约分销供应链中，我们可以得到零售商横向竞争下采购联盟的远视稳定结构如定理2所述。

定理2. 如果供应商提供两部收费制折扣契约，则分销供应链中零售商横向竞争下采购联盟的远视稳定结构为G。

此外，与定理1的证明类似，在供应商所提供的契约形式为d=10，e从0.1变化到1时，相互竞争的零售商联盟的远视稳定结构为大联盟G；而提供的契约形式为为d=-0.3，e从-0.9变化到-0.1时，相互竞争的零售商联盟的远视稳定结构为大联盟G；但是，如果提供的契约形式为d=-0.3，e=-1时，相互竞争的零售商联盟的远视稳定结构为两个零售商结盟M。

5 结语

本文针对由单一供应商和三个横向竞争零售商所组成的两层分销供应链系统，采用合作博弈论中描述远视参与者的最大一致集概念，在供应商所提供的两种特殊折扣契约下，分别研究了横向竞争零售商采购联盟的远视稳定结构。研究发现，当供应商提供线性折扣契约时，根据供应商提供的折扣比例不同，横向竞争零售商的采购联盟结构是不同的，当折扣比例较低(小于0.5)时，横向竞争的零售商会形成仅两个零售商联合采购的联盟结构，将第三个零售商排除在联盟之外；而当折扣比例较高(大于0.5)时，横向竞争的远视零售商将只会形成大联盟，以增强共同的竞争力。但是，当供应商提供两部收费制折扣契约时，无论供应商所提供的折扣比例如何变化，横向竞争零售商都以三个零售商联合采购的大联盟为稳定结构。此外，通过数值例子可以发现，当供应商提供其他形式的数量折扣契约时，相互竞争的零售商联盟的远视稳定结构为大联盟。

但由于零售商联合采购联盟的稳定结构受到诸多因素的影响，限于篇幅，本文没有进一步的展开讨论。如，本文没有考虑零售商之间的竞争强度、不同零售商规模的差异性对联盟稳定结构的影响，此外，需求受到广告、服务等其他因素影响时联盟稳定结构所发生的变化等都是值得进一步展开讨论的重要问题。总之，上游供应商数量折扣契约的制定，将对相互竞争零售商联合采购联盟的稳定结构产生重要影响，这是值得关注联合采购联盟发展的企业经理人和学者们不断探索的重要问题。

[1] Nalebuff B J, Brandenburger A. Co-opetition [M]. HarperCollins Publishers,1996.

[2] Hendrick T E. Purchasing consortiums: Horizontal alliances among firms buying common goods and services: What? Who? Why? How? [R]. Working Paper,Center for Advanced Purchasing Studies, 1997.

[3] Essig M. Purchasing consortia as symbiotic relationships: developing the concept of “consortium sourcing”[J]. European Journal of Purchasing & Supply Management, 2000, 6(1):13-22.

[4] Tella E, Virolainen V M. Motives behind purchasing consortia[J]. International Journal of Production Economics, 2005, 93-94:161-168.

[5] Ball D, Pye J. Library purchasing consortia: The UK periodicals supply market[J]. Learned Publishing, 2000, 13(1):25-35.

[6] Cachon G P. Supply chain coordination with contracts[M]//Graves S,de kok T. Handbook in operations research and management science: Supply chain management, North Holland: Amsterdam,2003:229-339.

[7] 周永务. 随机需求下两层供应链协调的一个批量折扣模型[J]. 系统工程理论与实践, 2006,(07):25-31.

[8] 许甜甜, 肖条军. 基于数量折扣的时滞变质物品库存协调模型[J]. 系统工程理论与实践, 2013,33(7):1690-1698.

[9] 刘斌, 马新迪, 张荣. 应急采购情形下短生命周期产品的团购策略分析[J]. 中国管理科学, 2013,(S1):183-189.

[10] 陈敬贤, 马志强, 孟庆峰. 线性量折扣方案下团购策略对渠道绩效的影响[J]. 中国管理科学, 2014,22(1):110-119.

[11] 刘春玲, 肖位春, 黎继子, 等. 基于Credit期权的集群式供应链采购模型及算法分析[J]. 中国管理科学, 2014，22(8):72-79.

[12] Hartman B C, Dror M, Shaked M. Cores of inventory centralization games[J]. Games and Economic Behavior, 2000, 31(1):26-49.

[13] Meca A, Timmer J, Garc, et al. Inventory games[J]. European Journal of Operational Research, 2004, 156(1):127-139.

[14] Guardiola L A, Meca A, Puerto J. Production-inventory games: A new class of totally balanced combinatorial optimization games[J]. Games and Economic Behavior, 2009, 65(1):205-219.

[15] Nagarajan M, Bassok Y. A bargaining framework in supply chains: The assembly problem[J]. Management Science, 2008, 54(8):1482-1496.

[16] Granot D, Yin Shuya. Competition and cooperation in decentralized push and pull assembly systems[J]. Management Science, 2008, 54(4):733-747.

[17] Nagarajan M, Sosic G. Coalition stability in assembly models[J]. Operations Research, 2009, 57(1):131-145.

[18] 郑士源, 王浣尘. 基于动态合作博弈理论的航空联盟稳定性[J]. 系统工程理论与实践, 2009, 29(4):184-192.

[19] 曾银莲, 李军, 刘云霞. 基于最大一致集的合作运输联盟稳定性分析[J]. 系统科学与数学, 2015(10):1219-1232.

[20] Granot D, Sosic G. Formation of alliances in internet-based supply exchanges[J]. Management Science, 2005, 51(1):92-105.

[21] Nagarajan M, Sosic G. Stable farsighted coalitions in competitive markets[J]. Management Science, 2007, 53(1):29-45.

[22] 周永务, 肖旦, 汤勤深, 等. 分销供应链中竞争零售商联盟的稳定性[J]. 运筹与管理, 2013，22(4):50-59.

[23] Ha A Y, Tong Shilu. Contracting and information sharing under supply chain competition[J]. Management Science, 2008, 54(4):701-715.

[24] Schotanus F, Telgen J, De Boer L. Unraveling quantity discounts[J]. Omega, 2009, 37(3):510-521.

[25] Chwe M. Farsighted coalitional stability[J]. Journal of Economic Theory, 1994, 63(2):299-325.

Stable Structure of Purchasing Coalitions with HorizontalCompeting Retailers in Distribution Supply Chains

XIAO Dan1, ZHOU Yong-wu2, SHI Xin-xiang3, LI Chang-wen4

(1.School of Business Administration, Guangzhou University, Guangzhou 510006, China;2.School of Business Administration, South China University of Technology, Guangzhou 510640, China;3.Institute of Guangdong Hong Kong and Macao Development Studies, Sun Yat-sen University Guangzhou 510275, China;4.Information College, Huaibei Normal University, Huaibei 235000,China)

Purchasing plays a very important role in the practical operations for some companies. Many companies will purchase jointly in order to reduce the operational cost. Although many purchasing coalitions collaborate on the procurement, they still compete in other fields such as order quantity or price. Therefore, there is an interesting problem needed to solve, that is, how the farsighted stable structure of purchasing coalitions will be. In a two-echelon distribution supply chain formed by a single supplier and three competing retailers, the farsighted stable structure of purchasing coalition among retailers is analyzed by using the concept of farsighted largest consistent set(LCS) in the cooperative game theory under different discount schedules. It is found that the stable structure of competing retailers’ purchasing coalition depends on the discount scale when the supplier provides a linear discount schedule. If the discount scale is low (less than 0.5), horizontal competing retailers will form a two-retailer purchasing coalition, the third retailer will be ruled, and if the discount scale is higher (more than 0.5), horizontal competing retailers will form the grand purchasing coalition, in order to enhance the competitiveness. However, when the supplier provides a two-part tariff discount schedule, the stable structure is always the grand purchasing coalition regardless of discount scale. In addition, it is also found that the grand coalition will be the stable structure for the farsighted retailers under other discount schedules by the numerical examples. This paper will provide some reasonable and operational suggestions for farsighted retailers form coalitions.

distribution supply chains; cooperative game; purchasing coalition; farsighted retailers

2015-09-07；

2016-05-30

国家自然科学基金资助项目(71131003)；广东省自然科学基金资助项目(2014A030310443)；教育部人文社会科学基金资助项目(15YJC630138，15YJC630053)；安徽省高等学校自然科学研究重点项目(KJ2015A335);广州市科技计划项目(201510010149)

史欣向(1981-)，男(汉族)，陕西西安人，中山大学粤港奥发展研究院、自贸区综合研究院，院长助理，副研究员，研究方向：公司治理、技术创新，E-mail:shixx3@mail.sysu.edu.cn.

1003-207(2017)04-0033-09

10.16381/j.cnki.issn1003-207x.2017.04.005

F224.3

A