震后应急供应问题与交通路网的协同优化模型

何新华，胡文发，周溪召，郑爱兵

(1.上海海事大学经济管理学院，上海 201306；2.同济大学经济与管理学院，上海 200092；3.上海理工大学管理学院，上海 200093；4.上海财经大学国际工商管理学院，上海 200043)



震后应急供应问题与交通路网的协同优化模型

何新华1，胡文发2，周溪召3，郑爱兵4

(1.上海海事大学经济管理学院，上海 201306；2.同济大学经济与管理学院，上海 200092；3.上海理工大学管理学院，上海 200093；4.上海财经大学国际工商管理学院，上海 200043)

地震的发生对交通路网的影响主要有两个方面，一是原有的交通路网遭到破坏，使交通路网的通行能力大大降低；二是地震突发事件发生后，受灾地区有大量的伤员需要运出接受救治，加上受灾地区由于救援工作需要大量资源，使路网的流量迅速提升。震后路网是这两种情况的叠加，极易发生严重堵塞现象。为避免和减少这种情况的发生，首先分析面向智慧城市和大数据环境下的协同供应效率系数的影响，构建考虑应急服务资源覆盖面最大和灾害损失最小的应急供应协同模型。其次，在分析应急车辆平均行程速度、路段饱和度、占有率和排队长度比等约束条件的基础上，构建震后应急交通路网协同优化模型。最后案例验证了所提出的协同优化模型的有效性。研究成果将对应急交通控制和管理实践提供理论依据和解决方案。

应急供应；应急服务资源；震后应急交通路网；协同供应效率系数

1 引言

应急服务资源供应是应急救援措施非常重要的一个部分，而震后应急交通路网是应急救援的关键资源之一。如何协调震后应急交通路网资源的高效使用，对救灾工作的展开非常重要。地震等突发事件的发生对交通路网的影响有两个方面，一是原有的交通路网遭到破坏，使交通路网的通行能力大大降低，另一个方面是地震突发事件发生后，受灾地区有大量的伤员需要运出接受治疗，而且受灾地区还需要大量的应急服务资源，使路网的流量迅速提升。震后应急交通路网是这两种情况的叠加，因此非常容易发生堵塞现场，这种堵塞情况最容易发生在交通路口和遭受地震严重破坏的路段。为避免这种情况的发生，必须用科学的方法和先进的技术，最大限度的发挥交通路网的通行能力，使应急服务资源能够及时的运送到灾民手里，最大程度的发挥应急指挥系统的有效性。

在现实中，地震等突发事件会给灾区带来巨大的损失，而高效快速的应急服务资源供应机制能够有效的减少灾害带来的损失。目前有很多学者从事应急突发事件的研究，已取得很多成就。比如在应急物资的联合供应问题方面，就有Sheu[1]等通过聚类优化方法来研究解决灾后的应急救援需求，在建立一个混合模糊模型的基础上分析紧急救援期受灾地区需求资源的联合分配方法。部分学者在应急服务资源选址、配置及其他应急物流方面的应用进行了相关研究，比如Liu Wenmao等[2]在通过建立应急选址模型来分析应急物流配置问题。对交通路网的控制进行研究成果也很多，具有突出贡献的是Wong和Yang Hai[3]首次在分析单个信号交叉口车辆通行能力的基础上，对交通路网的信号控制网络的备用能力展开研究并给予定义。接下来许多学者对交通路网的流量均衡和控制问题进行研究。比如Chiou[4]运用非线性规划的方法建立了目标函数，该目标函数考虑了网络平衡与交通控制中的弹性需求。而在大城市中，交通流的预测对缓解交通通行状况非常重要，但是之前的研究方法无法准确、快速和稳定的预测交通流。于是，Kong Xiangjie等[5]认为运用浮动车轨迹方法可及时预测交通流，并提出运用粒子群算法来计算模型，最后通过案例来证明模型的有效性。但有些学者认为当前的研究方法无法解释交通流的本质规律，因此对现有的预测交通流方法进行的研究，提出一种深度学习的短时交通流预测模型，并通过许多算例证明预测模型的有效性[6-11]。还有些学者已有效解决部分震后应急物资的配送问题，比如刘长石等[12]综合考虑救灾点所在地理位置和地形导致的应急车辆行驶时间的随机性的基础上研究震后应急物资配送的路径问题，以实现震后应急物流联合决策。同时较多的研究主要是论述应急调度协同优化方面的概念特征和它们带来的影响[13-15]。研究表明应急供应问题和应急交通路网控制问题的各种决策所面临的重要难题显然是现有研究成果无法解决的。

综上所述，这些学术成果为进一步开展本文研究提供了丰富的文献参考和有益的借鉴，仍存在如下问题：在震后应急救援和救灾工作的有效时间内，对于应急供应效率的预估不足；无法准确和快速的预估应急交通流，不能最大限度的发挥交通路网的通行能力使应急服务资源能及时送给灾民；不能完全解析出影响因素对应急交通路网的影响机理；所建目标函数也缺乏对各利益相关者同时达到优化的考虑。

因此，本文综合考虑多种影响因素，针对震后应急交通的特殊情况，首先分析以应急服务资源集散中心、应急服务资源转运中心和应急服务资源发放中心为应急交通协同网络的应急任务，构建应急供应模型；其次，为确保震后应急服务资源的供应和避免交通路网出现堵塞，在分析应急车辆平均行程速度、路段饱和度、占有率和排队长度比等约束条件的基础上，构建震后应急交通路网协同优化模型，研究成果将对应急交通控制和管理实践提供理论依据和解决方案。

2 问题描述与假设

假设在应急服务资源供应过程中，通过利用智慧交通应急指挥中心可实现对应急服务资源的定位、获取实时交通道路信息和对资源运输过程的实时定位监控，提高应急指挥中心获取相关应急所需信息的能力，使得应急资源的调度工作能够高效地、安全地开展。各地区已经建立较健全的：(1) 应急服务资源集散中心S，集合S={Si|i=1,2,…,m}；(2)应急服务资源转运中心W，集合W={Wj|=1,2,…,l}；(3)应急服务资源发放中心D，集合D={Dk|k=1,2,…,n}。这些中心形成应急交通协同网络，见图1。

本文把地震灾害发生后的应急工作划分为三个阶段：第一阶段，是在地震发生的第一时间，迅速将应急服务资源集散中心S的资源，根据实际情况和环境进行合理有效的整合；第二阶段，随着智慧城市网络和大数据技术的蓬勃发展，使得应急服务资源转运中心W已经有效的将分散在各区域的应急资源储备节点连接起来，因此本阶段要合理有效的转运应急储备资源，从而有效并且高效的提高应急资源的利用效率、降低交通运输成本；第三阶段，在救援和救灾工作有效的时间内，对应急服务资源发放中心D可能会需要的应急资源进行有效地确认，为应急资源的科学及时有效并且高效的调度提供强有力的保障。

因此，本文决策问题是：在满足地震后的各受灾点的基本需求量、供应时间受限、供应量受限、损失最小等条件下，确定应急服务资源的协同供应路径和方案。由此作如下假设：

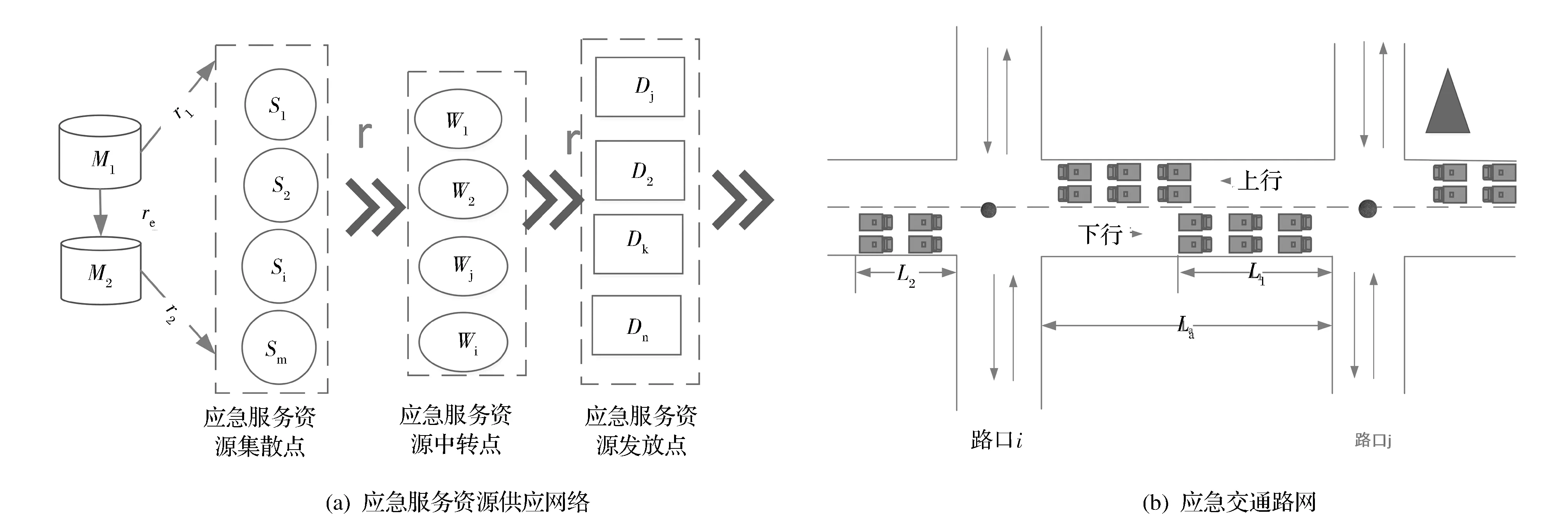
图1 智慧城市和大数据环境下的应急交通协同网络

假设1：本节研究问题主要是集中在震后，即震前应急服务设施的布局，采购等方面成本不在本模型的考虑之中；

假设2：根据灾害发生的突发性实际情况以及平时应急服务资源布局成本，灾前的应急服务资源是有限的，即无法满足灾害开始阶段所有受灾点的应急服务资源需求；

假设3：考虑到运输效率和实际的交通状况，应急服务资源需要转运两次，受灾地区才能拿到应急服务资源，即先从省级或者市级应急服务资源中心运送到县级转运中心，再从县级应急服务资源转运中心转运到应急服务资源发放点，即应急服务资源供应有三级供应网络节点；

假设4：应急服务资源的运输能力是无限的，即震后可以组织到足够多的运输工具将应急服务资源转运到受灾点；

假设5：地震灾害会对道路造成巨大的破坏，因此模型考虑的道路的实际运输能力，可以通过卫星遥感和飞机航拍技术及时了解道路的损坏程度。

所以，本文的研究中着重考虑协同供应效率系数这个变量，考虑灾害损失最小的前提下再考虑应急服务资源供应覆盖率最大化，保证最基本的救灾需求和应急服务资源供应的平衡性，实现面向智慧城市和大数据环境下的应急交通协同问题的研究。

3 模型构建和求解

3.1 震后应急供应模型

由于地震灾害的弱经济性，震后应急服务资源供应的成本将变得不再重要，应急速度、应急时间和救援覆盖范围等将成为最为重要的因素。本文借鉴Liu Wenmao等[2]提出的框架体系，建立应急供应协同模型。下面给出模型所涉及的相关变量和参数的定义：

应急服务资源供应的首要目标是在规定的需求时间段内尽可能将应急服务资源供应到各灾害需求点，减少灾害造成的损失，同时考虑应急服务资源覆盖范围的问题，所建立的模型如下：

(1)

(2)

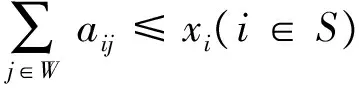
(3)

(4)

(5)

aij≤Muij∧ajk≤Mvjk(i∈S,j∈W,k∈D)

(6)

(7)

(8)

目标函数式(1)表示最大程度地覆盖和满足灾区应急服务资源需求,即模型考虑了覆盖范围。目标函数式(2)表示震后应急灾害造成的损失为最小,应急灾害造成的损失与灾害的等级、受灾地区的人口密度以及灾害发生后应急服务资源的满足程度是有联系的。式(3)为Si运到Wj的量不超过其总供应量；式(4)为Wj运到Dk量不超过储备量与补充量累加之和；式(5)为Dk的需求量约束和满意度约束；式(6)为只有0-1变量取1时，相应的应急供应量才可能取正；式(7)为只有Si到Wj的供应总时间小于与Dk相通的各需求点的最大配送极限时间时，才能在Si和Wj之间实现供应配送；式(8)为Si到Wj再Dk的运输总时间小于Dk的配送极限时间约束。

3.2 震后应急供应下的协同优化模型

由于在应急服务资源的协同供应过程中，应对突发事件的重要支撑是应急指挥中心可以及时获取应急服务资源供给信息、实时灾害情况、交通道路通行状况信息以及对应急服务资源运输过程中的实时定位监控等信息数据。同时地震对路段和路口产生了重大破坏以及救援的需要可能会导致交通流量在短时间内会迅速增加，按照原有的供应方案实施非常困难，随着路网应急车辆的不断增加，在达到某一阈值时，路网或路口就会出现堵塞。在这种状态下，要及时实施应急服务资源供应协同优化方案，从时间和空间上对应急交通网络进行协同优化管理，该优化目标可用如下公式表达：

(9)

目标函数式(9)的约束条件处理如下：

(1)震后考虑应急救援的需要，路口有应急救援人员需要穿越马路。因此，为了确保应急人员安全通过马路的需要，每个路口的应急交通控制信号的绿灯时间是一个给定值e(e≤20s)。设gi为相位i的应急绿灯时间，m为路口周期内的相位数；T为应急救援区域内的周期时长。每个路口的相位配时参数约束条件为：

e≤gi≤T-(m-1)e,(i=1,2,…m)

(10)

(2)应急救援区域内各路口的信号周期时长T：

(11)

(12)

式(11)-(12)中，n为应急救援区域路口数目；Ti为路口i的周期，可通过Webster方法求得；L为损失时间(s)；Y为应急救援区域路口信号相位的总应急车流量比；yi为相位j的应急车流量比；qd为应急车流量；Sd为饱和流量。

(3)上行相位差Ψ上和下行相位差Ψ下表示为：Ψ上+Ψ下=T，0≤Ψ上≤T。

(4)由于震后受灾地区需要大量应急服务资源，路段应急车辆的流量不断积累，当排队长度超过路段长度，就会造成下一个路口的堵塞。智慧城市和大数据环境下的震后路段上的应急车辆主要由式(13)所表示，具体表现形式见图1(b)。

Lα=L1+L2

(13)

式(13)中，L1为路口j下行应急车辆的排队车辆数；L2为路口i下行应急车辆的排队车辆数。设应急路网中路段α的长度为Lα，相邻的两个路口i和j的统一信号周期为T，相邻的两个路口i和j的通行时间为gi和gj，等待时间为ri和rj，相邻的两个路口i和j之间的相位差为ψ，路段上应急车辆的平均车速为ϑi，应急车辆的停车波为αi，应急车辆的启动波传播速度为βj。若路口i绿灯结束后，则最后驶离的应急车辆经过t1达到排队队尾；若路口j绿灯结束，经过(ψ+gj)时间，此时随着最后一辆应急车驶出路口j的停车线，未驶离或刚到达停车线的应急车辆以波速αi向后排队，又经过一段时间t2，形成排队长度L2。由此可得：

(14)

当路口i绿灯亮起后，停车线处的应急车辆开始陆续驶离路口i，并以速度αi向路段下游行驶，经过时间t1，驶离的第一辆应急车到达下游车队队尾；第一应急辆车受到下游排队的应急车辆的阻碍，形成停车波，并以波速αi向后排队，又经过一段时间t3，形成停车排队长度L2；当下游路口j的绿灯亮起时，启动波开始以波速βi向后传播，并经过时间t4与停车波相遇。由此可得：

(15)

为了确保应急救援的效率，必须控制路段应急车辆的排队长度，保证其最大排队长度不得超过路段长度，需满足：

(16)

式中，γα为路段α的最大应急交通流压缩比。

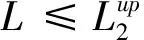
(17)

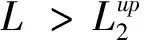
(18)

(5)应急车辆的行驶时间

应急车辆行驶时间包括应急车辆在路段上的通行时间ta,γ(t)和应急车辆在路口节点处的通行时间ta,s(t)。Lj为路网中某路段j的长度；ϑj为路网中某路段j的平均速度。若某路段或者路口出现应急车辆堵塞，那么应急车辆的总通行时间包括正常通行时间ta,γ,f(t)和排队等待时间ta,γ,c(t)；Lij为应急车辆等待的长度，该里程可以通过卫星定位技术获得。

在应急车辆正常通行状态下，通行时间为ta,γ(t)=Lj/ϑi；应急车辆经过两个路口的通行时间为ta,γ(t)=(Lj-Lij)/ϑi。

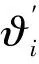
(19)

应急车辆在路网中节点处的等待时间ta,s(t)是由应急信号控制措施引发路网应急交通流间断导致的车辆行驶时间损失[7]。本文选用HCM2000(HighwayCapacityManual2000)延误模型计算路口应急车辆排队延误[8]。该模型将应急车辆在路口的平均延误分为：均匀控制延误、增量延误、初始排队延误，计算公式如下：

(20)

3.3 模型求解

(1)协同供应效率系数的计算分析

由于地震发生后，救援地的总供应量不一定能全部满足所有受灾点的需求，因此会使某些受灾点的总供应量xk小于或者等于需求量zk，即dk≤zk。因此需要对每个受灾点的供应情况进行效率评估。

定义1：地震后的各受灾点对应急服务资源的当量需求量为该受灾点的实际需求量与需求紧迫程度的乘积(zk·πk)。则受灾点的理想分配效率mk是该受灾点的当量需求量在所有受灾点的总当量需求量中所占的比重。即：

(21)

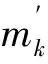
(22)

(23)

在得到每个受灾点的独立供应效率系数后，就可计算整个应急协同供应分配方案的协同供应效率系数，协同供应效率系数为f(φk)，则其计算公式为：

(24)

推论1：当每个震后受灾点的独立供应效率系数相同时，协同供应效率系数为1。

推论2：协同供应效率系数的取值范围是[0,1]。

推论1的证明：

(2)多目标模型的求解

要使得将应急服务资源供应到各灾害需求点的供应时间最少，同时减少灾害造成的损失，且还有满足应急服务资源覆盖范围尽可能大的目标，这个多目标同时达到是不可能的，由此需要在几者之间寻找平衡。对于这个多目标的求解方法，本文采用一种改进的功效系数法对这里的多目标进行处理。假设μ为模型的解向量，G为μ的可行域，则多目标模型的求解步骤如下：

步骤1，分别计算出目标函数值的上界和下界：

(25)

(26)

(27)

(28)

(29)

(30)

步骤2，设

(31)

步骤3，得出最终模型：

(32)

4 应用分析

(1)案例

以我国2008年汶川地震为例，地震主要对成都市、绵阳市、德阳市、广元市、阿坝州、雅安市六个地区造成了严重的损失，因此，论文假设地震主要对成都市、绵阳市、德阳市、广元市、阿坝州、雅安市六个地区造成了严重的损失，主要考虑这六个受灾点的供应情况，其应急服务资源需求量见表1。另外，非一次性消耗资源属于不便于同一次性消耗资源组合，因此，该案例不考虑非一次性应急服务资源供应情况。

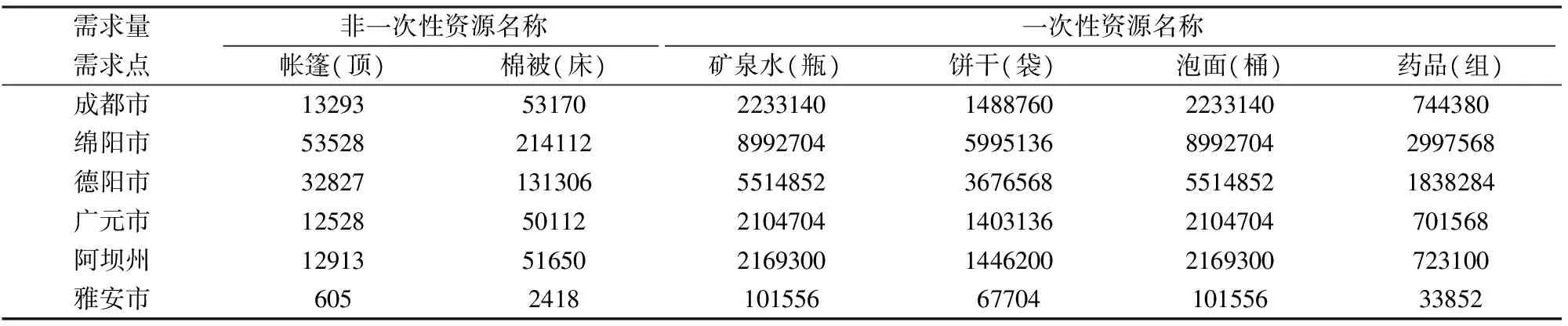
表1 应急服务资源的需求数量

为了使案例数据更好的适应模型，本文假设不同种类的应急服务资源在应急服务资源集散点转运到应急服务资源中转点时进行组合，即对各种应急服务资源进行打包，按每人每天的需求量打包一份，以便资源运送到受灾点时更好的发放到受灾群众手里，基于以上假设，受地震影响较大的成都市、绵阳市、德阳市、广元市、阿坝州、雅安市六个地区应急服务资源组合需求量分别为10000、50000、30000、10000、10000、1000组。设共有六个应急服务资源转运中心，分别是W1、W2、W3、W4、W5、W6，根据应急布局方案，转运中心储备一定量的应急服务资源，具体见表2。设共有三个应急服务资源集散点，分别是S1、S2、S3，根据应急服务资源布局要求，应急服务资源集散中心储备一定量的应急服务资源，具体见表3。

表2 转运中心应急服务资源储备量

表3 集散中心应急服务资源储备量

从表2、表3可知，总的应急服务资源需求量为111000组，目前的应急救援系统能够提供的数量为85000组，无法满足灾情的需要，但是满足率已经达到了76.57%，已经达到了救灾的需求；根据救灾实际情况，假设救灾应急极限时间为24小时，再结合各应急点的受灾损失程度，即应急服务资源需求系数，可得出应急点的实际需求极限时间，具体应急极限时间见表4。

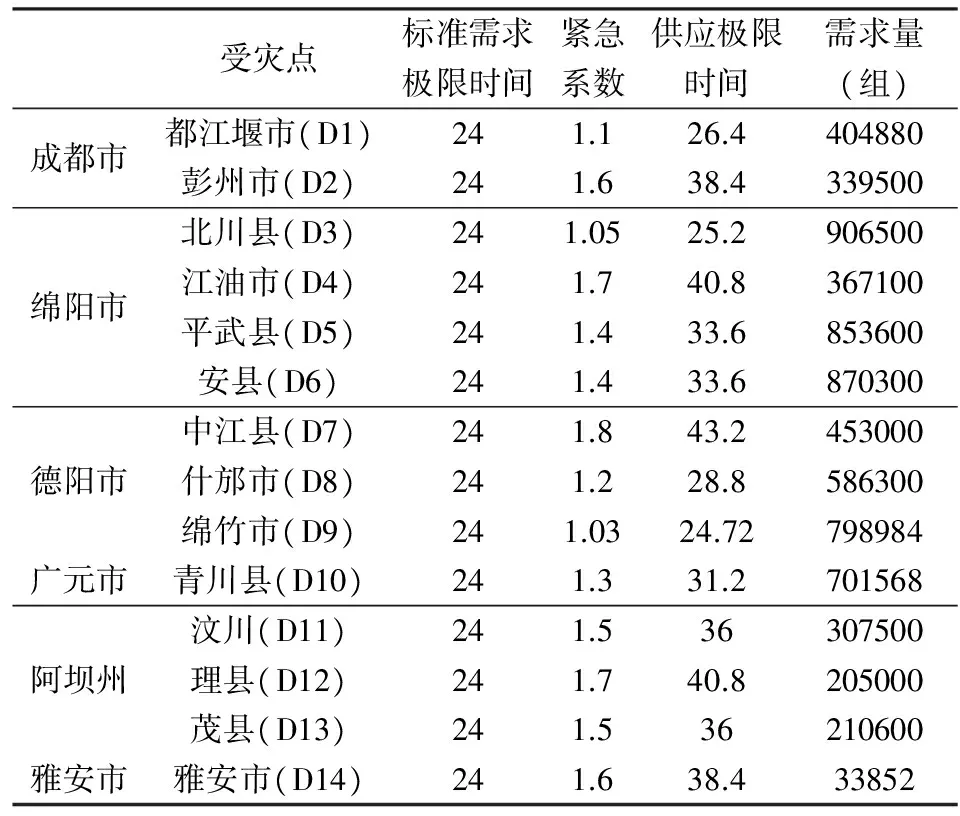
表4 各受灾点应急服务资源需求系数

模型中假设的三种运输方式的速度v1、v2、v3假设为5km/h、30km/h、200km/h。各集散中心到转运中心的空间距离如表5、表6所示。

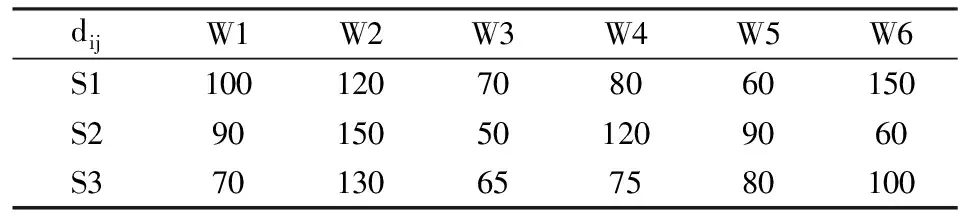
表5 各集散中心到转运中心的空间距离(km)

表6 各转运中心到各受灾点的运输距离(km)

假设通过卫星遥感和飞机航拍，获取了各级节点之间的道路破坏。如表7、表8所示。

表7 集散点到转运中心的道路破坏率

表8 转运中心到受灾点的道路破坏率

表9 震后受灾点路网基本参数

(2)选取震后受灾点的区域路网和参数设置

设该区域路网包含9个路口，12条路段。该区域路网中各路段的基本参数情况如表9所示。

利用MATLAB8.3a，按照改进粒子群算法编程，设最大迭代次数为1000、粒子群规模为40，运行程序10次求解得目标函数值均值为119457.3，分布情况如图2-3所示，可以看出用该算法每次求得的解比较接近于平均值，全部分布在区间[116000，124000]之间，且误差比例都控制在4%以内，说明该算法具有较强的稳定性。

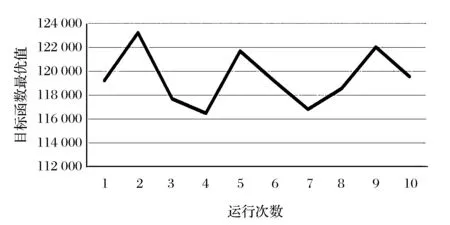
图2 改进粒子群算法

图3 误差比例

(3)结果分析

取一组接近平均值的最优解，得最优应急供应方案，如表10和表11所示。

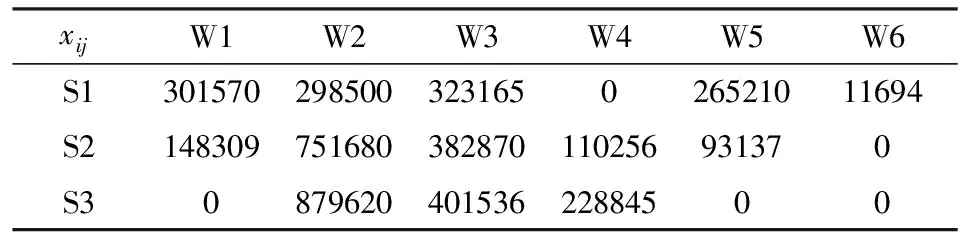
表10 各集散点到各转运中心的量

表11 从转运中心供应应急服务资源到各受灾点的量

计算各受灾点的应急服务资源满足率Π=(0.90，0.84，0.90，0.90，0.82，0.87，0.82，0.79，0.90，0.89，0.72，0.75，0.86，0.80)。根据计算可得Π≥0.7，各个应急救灾点的应急服务资源的满足率都在70%，说明提出的应急服务资源集散中心、转运中心和受灾点的供应网络模型在应急服务资源供应覆盖率最大和灾害损失最下的多目标模型能达到应急救灾的需要。

该地区在震后5小时内应急车流量迅速增加，具体数据见表12。

通过表12可知，路段R1、R2、R4、R9、R10在某次震后5时发生堵塞现象，因此，应该及时启动堵塞路段的应急交通协同优化模型。表12的数值输入到算法中，运行得到堵塞路段路网应急交通协同优化值，如表13和表14所示。

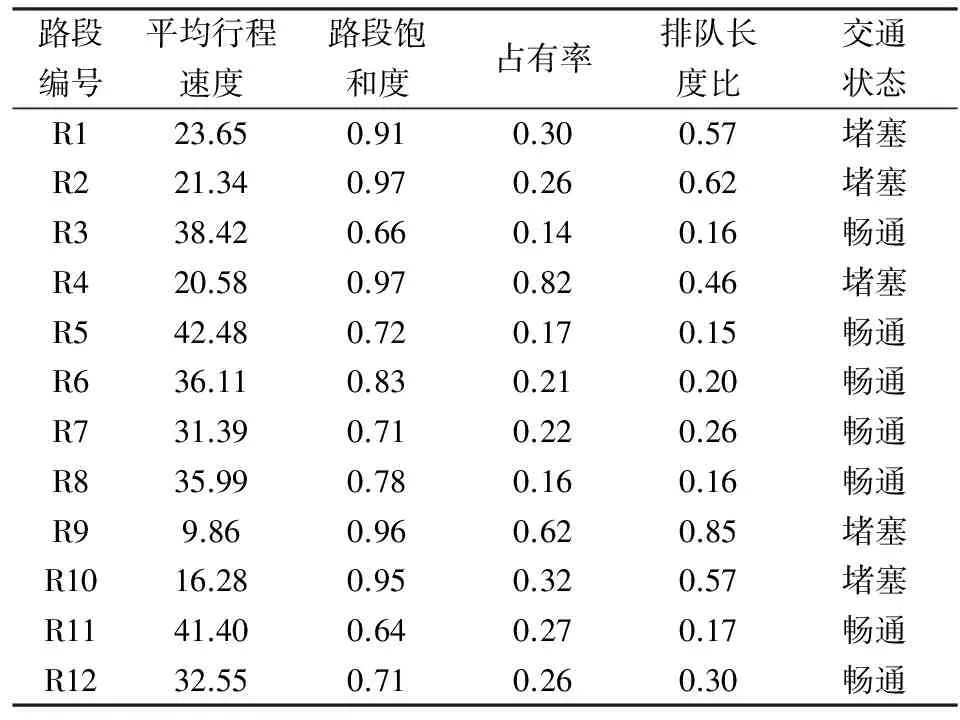
表12 震后路网动态应急车辆监测结果

表13 信号配时参数求解结果(s)

表14 路段参数求解结果

为了进一步说明所提出的震后应急交通协同优化模型的可用性，分别用应急车辆平均行程速度、路段饱和度、占有率和排队长度比四个指标与优化前的四个指标进行对标，分别见图4～图7。

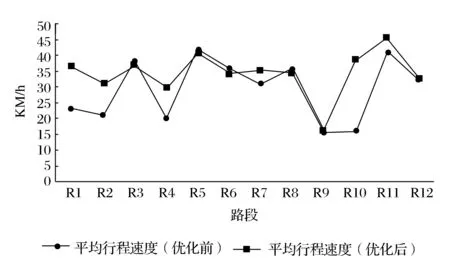
图4 优化前后各路段平均行驶速度对比图

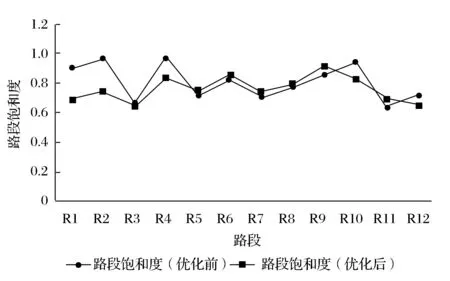
图5 优化前后各路段饱和度对比图

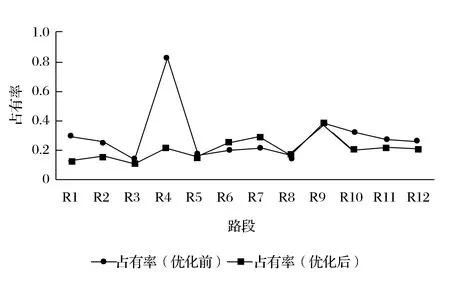
图6 优化前后各路段占有率对比图

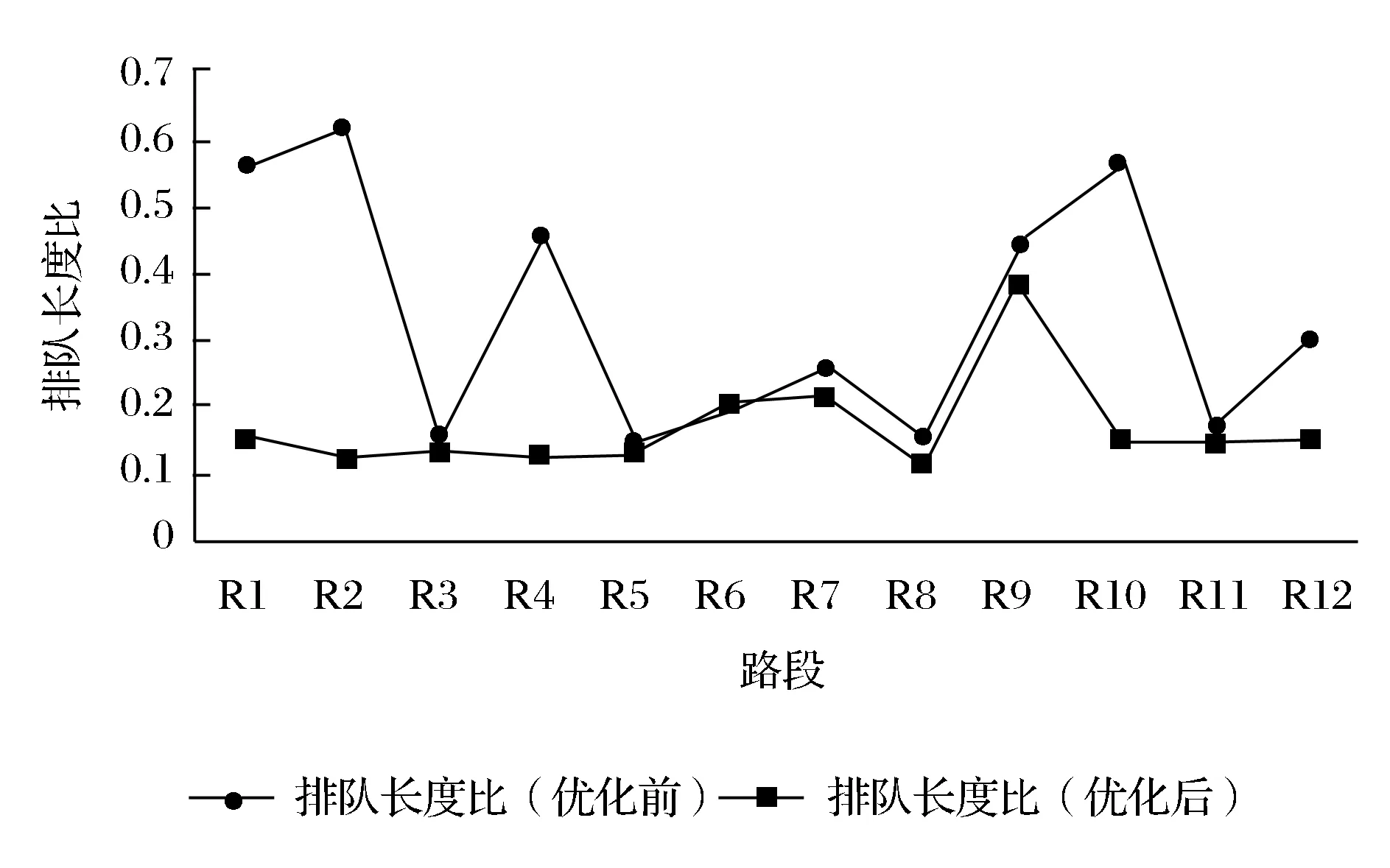
图7 优化前后各路段排队长度比图

由图4可知，优化后R1，R2，R4，R10路段的平均行驶速度明显变快，只有R9路段的平均行驶速度没有得到明显的提升。由图5可知，优化后R1，R2，R4，R10路段的饱和度有很大幅度的降低，只有R9路段的饱和度没有得到明显的降低，部分路段饱和度上升。从图6可知，优化后R1，R2，R4，R10路段的路段占有率明显降低，只有R9路段的路段占有率没有得到明显的降低，部分路段有一定程度的提升。从图7可知，优化后R1，R2，R4，R10路段的排队长度比明显降低，只有R9路段的排队长度比没有得到明显的降低，部分路段有一定程度的提升。

综上所述，震后对路网实施应急交通协同优化方案，路网中各路段的流量得到了均衡，协同前相对拥挤的路段经过协同优化后，将流量分配到别的路段上，避免造成拥挤蔓延。因此，所提出模型是有效的。说明应急服务资源供应覆盖率最大和灾害损失最下的多目标模型能达到应急救灾的需要，能及时快速满足应急交通协同优化管理的需要。

5 结语

本文在分析智慧城市和大数据环境下的应急交通协同优化框架的前提下，提出相关假设，分析了应急交通网络的协同供应效率系数，并构建以应急服务资源覆盖范围最大和受灾点总损失为最小的应急供应模型。同时，根据应急管理的实际需要和理论文献构建了应急服务资源集散点、转运点和受灾点的节点的供应网络，在分析应急车辆平均行程速度、路段饱和度、占有率和排队长度比等约束条件的基础上，构建震后应急交通路网协同优化模型。最后利用案例验证了所提出优化模型的有效性。

研究表明震后应急交通流量是一个动态的过程。可以运用通讯技术如传感器等获取实时交通数据信息，以便于在调整、更新应急交通方案时及时的考虑这些最新信息。论文所研究的震后应急交通路网协同优化过程可以通大数据技术解决。通过大数据技术获取和处理的实时更新的最优解决方案是对震后应急交通控制非常重要的，它可以防止应急救援车辆行驶到已经拥挤的路段或路口；它还可以通过应急方案引导，减少交通拥堵。研究成果对于提高交通管理水平、制定应急交通策略和协同优化应急管理具有重要的理论价值和现实意义。

[1] Sheu J B. An emergency logistics distribution approach for quick response to urgent relief demand in disasters [J]. Transportation Research Part E:Logistics and Transportation Review, 2007, 43(6):687-709.

[2] Liu Wenmao, Hu Guangyu, Li Jianfeng.Emergency resources demand prediction using case-based reasoning[J].Safety cience,2012,50(3):530-534.

[3] Wong S C,Yang Hai. Reserve capacity of a signal control road network[J].Transportation Research,1997,31(5):397-402.

[4] Chiou S W. Optimization of a nonlinear area traffic control system with elastic demand [J]. Automatica, 2010,46(10):1626-1635.

[5] Kong Xiangjie, Xua Zhenzhen, Shenb Guojiang, et al. Urban traffic congestion estimation and prediction based on floating car trajectory data[J]. Future Generation Computer Systems, 2016, 61: 97-107.

[6] Yang Zhaosheng,Mei Duo,Yang Qingfang,et al. Research on traffic flow prediction model for large-scale road network based on cloud computing[J].Mathematical Problems in Engineering, 2014,2014(3):1-8.

[7] 陈绍宽，郭谨一，王璇,等.交叉口延误计算方法的比较[J].北京交通大学学报,2005,29(3)：77-80.

[8] 庄焰，曾文佳.信号交叉口延误计算模型研究[J].深圳大学学报(理工版),2006,23(4)：309-313.

[9] 王嘉祺，程建川，王昊.信号交叉口增量延误分析[J].交通与计算机,2005,23(5)：13-16.

[10] 孙智源, 陆化普,张晓利，等. 城市交通控制与诱导协同的双层规划模型[J]. 东南大学学报(自然科学版), 2016, 46(2): 450-457.

[11] 罗向龙,焦琴琴,牛力瑶,等. 基于深度学习的短时交通流预测[J]. 计算机应用研究, 2016, 34(1): 1-5.

[12] 刘长石, 彭怡, 寇纲. 震后应急物资配送的模糊定位-路径问题研究[J]. 中国管理科学，2016, 24(5)：111-118.

[13] Allwinkle S; Cruickshank P. Creating smarter cities: An overview[J].Journal of Urban Technology,2011,18(2):1-16.

[14] 何新华,胡文发,许长延,等.考虑随机性与模糊性的应急服务供应链转运策略[J].山东大学学报(理学版), 2016, 51 (12): 67-77.

[15] He Xinhua, Hu Wenfa. Modeling relief demands in an emergency supply chain system under large-scale disasters based on a queuing network[J]. ScientificWorld Journal, 2014,(2):1-12.

Emergency Supply Problems and Collaboration Optimization ofEmergency Traffic Network after Earthquakes

HE Xin-hua1，HU Wen-fa2，ZHOU Xi-zhao3，ZHENG AI-bing4

(1.School of Economics Management, Shanghai Maritime University, Shanghai 201306, China;2.School of Economics and Management, Tongji University, Shanghai 200092, China;3.University of Shanghai for Science and Technology, Shanghai 200093, China;4.School of International Business Adminstration,Shanghai University of Finance and Economics,Shanghai 200433)

An earthquake often has impact on a traffic network from two aspects. The first one is a wide damage of theexisting transportation network which would decrease traffic capacity dramatically and cause frequent traffic congestions, and the second one is a soaring demand of transportation to deliver a great deal of injured people to other undamaged areas in a short time and to import many emergent resources to the damaged areas. Accumulation of above impact would worsen transportation reliability and reduce transportation capability of the traffic network. In order to avoid those adversities, based on recognizing traffic network properties under emergency conditions after an earthquake, a framework of emergency service resource supply and supply problems of emergency service resources after earthquakes are considered in this paper. An Emergent Transportation Collaboration Network (ETCN) is presented, which consists of a collection center of emergent service resources, a transit center of emergent service resources and distribution center of emergent service resources. All emergent activities in ETCN are classified into three working stages, and a Collaboration Supply Efficiency (CSE) coefficient to describe their relationships is introduced. Based on ECTN and CSE coefficients, an Emergent Supply Collaboration Model (ESCM) is developed, whose objectives are to maximize coverage area of emergent service resources and to minimize disaster loss. In order to ensure supplying emergent service resources and avoiding traffic congestions, a collaboration optimization model of emergent traffic network after earthquake is further developed from ESCM considering constraints of average transportation speed of emergency vehicles, road saturation, occupation ratio and queue length. Then, it is discussed that the changing principle of occupation ratio and queue length by variation of transportation speed of vehicles under emergencies. In the end, a case study is applied to testify a collaboration optimizationto ensure supplying emergent service resources. A numerical example demonstrates the proposed model is effective and the improved algorithmis efficient.This paper would be a theoretical base and potential practice solution for emergency traffic control and management.

emergency supply; emergency service resources; emergency traffic network after an earthquake; collaborative supply efficiency coefficient

2016-06-30；

2017-01-08

国家自然科学基金资助项目(71473162，71371145，71102043，61273042)；上海市教育委员会创新项目(14ZS123)

何新华(1973-)，女(汉族)，湖北天门人，上海海事大学经济管理学院博士，副教授，硕士生导师，研究方向：应急供应链与交通控制研究，E-mail：xhhe@shmtu.edu.cn.

1003-207(2017)04-0104-11

10.16381/j.cnki.issn1003-207x.2017.04.013

U491;C931

A