改进的基于极大似然估计的码环鉴别器设计

王昕洋, 范胜林, 宋 恺, 侯 豆

(南京航空航天大学自动化学院, 南京 211106)

0 引言

全球导航卫星系统(GNSS)是一种重要的空间基础设施和战略资源,在国家的军事领域和民用领域发挥着越来越重要的作用。但是,GNSS接收机的应用环境日趋复杂,例如,在高动态载体活动的过程中,导航卫星的信号会产生剧烈的变化;在高楼林立的城市或者是树木丛生的森林,导航卫星的信号又时常会受到遮蔽和阻塞。这样的情况说明,GNSS接收机的鲁棒性至关重要[1-2]。信号跟踪是接收机中最为重要,同时也是最为脆弱的环节。所以,其跟踪性能就在比较大的程度上取决于其跟踪环路的鉴别器函数[3]。

码跟踪环路,即码环,其主要功能是保证接收机环路产生的复制C/A码与接收到的C/A码保持相位一致,从而剥离C/A码,得到接收信号的码相位值和伪距值[4]。为了提升跟踪环路的工作性能,提高码环鉴相器的可用性和稳定性,国内外学者进行了大量的研究工作。同钊等在构建了一种包含最大时延信息的超前支路码环的基础上,消除卫星信号的短延迟多径干扰[5]。然而,传统基于非相干的码环会受非相干积分值中包含的均值非零噪声的影响,会导致一步延迟效应和延时误差,影响环路精度和稳定性。

对于时不变系统,且处于平稳噪声和恒定参数的条件下的系统而言,极大似然估计能够给出一致的有效估计[6-7]。由此,文中在以上工作的基础之上,又引入了Won等[8]提出的基于极大似然估计器(maximum likelihood estimator,MLE)的跟踪算法,并将参数的极大似然估计值进行α滤波平滑,提出了一种改进的基于极大似然估计的码环鉴别方法。最后利用实测GNSS信号,在软件接收机上进行算法性能的测试和验证。预期这种方法可以有效降低基带跟踪环路的码环估计误差,提高码鉴相器滤波精度。这对导航接收机码跟踪环路性能的提升,接收机稳定性的提高有重要意义。

1 改进的基于极大似然估计的软件接收机跟踪环路结构

1.1 传统的跟踪环路结构

一般而言,传统接收机的跟踪环路的实现形式通常是延迟锁定环路(DLL)和载波鉴相环路(PLL)的搭配使用,大致结构如图1所示。接收机跟踪信号的最终目的是为了从码环中得到伪距值,载波环的作用其实是用来帮助码环剥离中频信号中的载波。

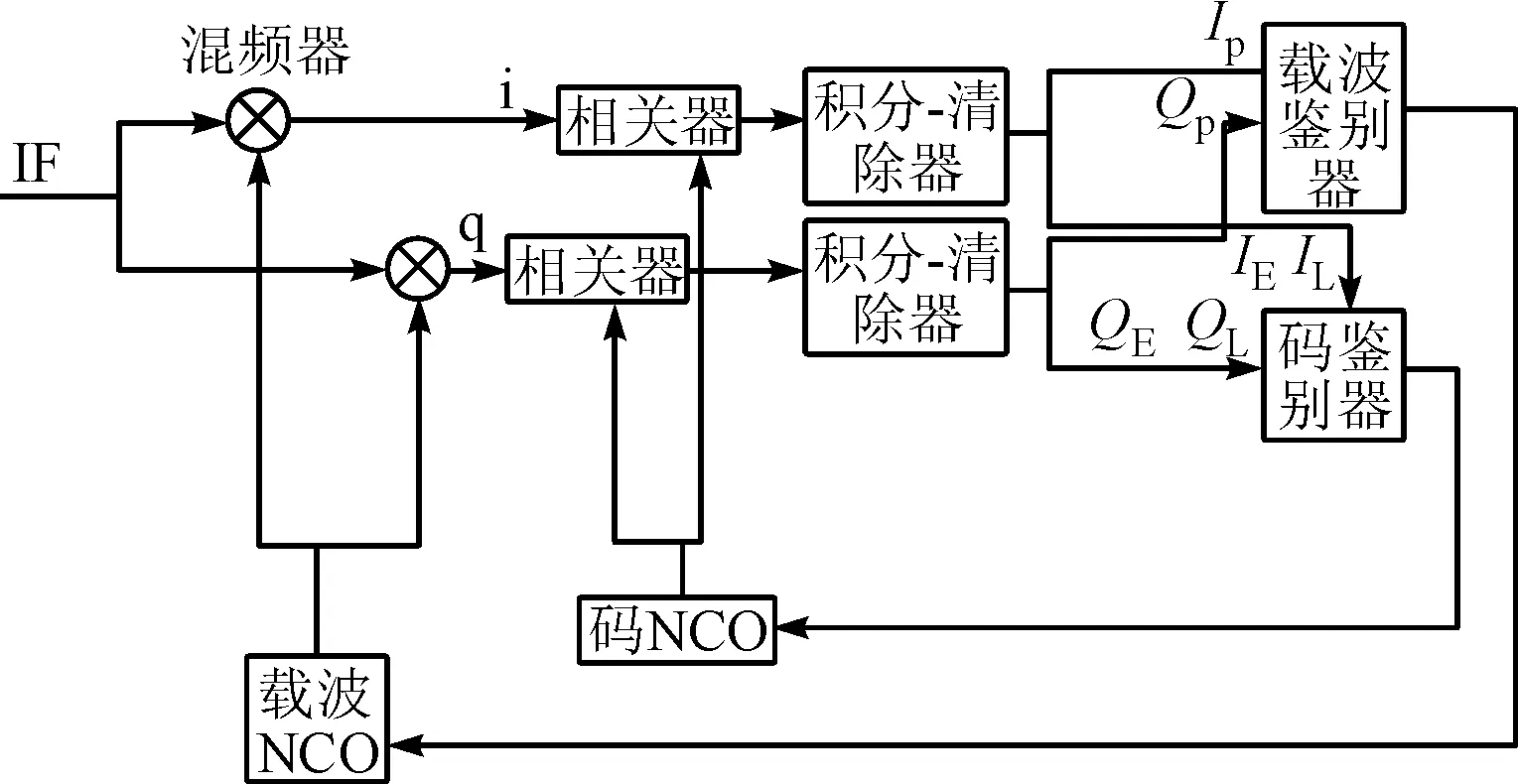
图1 传统接收机跟踪环路

1.2 改进的基于极大似然估计的跟踪环路结构

极大似然估计法是参数估计方法之一,它的基本思想是,已知某个随机样本满足某种随机分布,但是并不知道它的任何先验信息,通过若干次实验,由观测值来估计该参数[7]。对于导航卫星信号而言,当观测时间比较短(如1 ms)时,就可以认为,导航信号中的码相位近似为一个常数。于是,就可以利用极大似然估计法进行最优估计了。用MLE代替原环路中的码鉴相器,并对鉴相结果作α滤波,改进的跟踪环路结构如图2所示。

图2 改进的接收机跟踪环路

2 改进的基于极大似然估计的码环鉴相器设计

2.1 极大似然码鉴相函数的设计

在时不变系统中,极大似然估计可以给出一致有效的估计,当噪声平稳且参数恒定时,可以获得最佳的估计性能。想要利用极大似然法,首先需要构造待估参数的似然函数。典型GNSS中频数字信号可以表示为:

r(k)=A·C(k-τ)·cos[2πT·ω·k+φ]+nk

(1)

式中:A为中频信号幅值;C为伪随机码;T为采样间隔;ω为载波频率,由中频频率fIF加载波多普勒频移fd得到;φ为载波相位;nk是高斯白噪声;τ为码相位延迟。

虽然码相位反映的是载体和卫星的相对位置,然而τ并不是一个独立的随机变量,需要建立τ和fd的联合条件概率密度。则假设基带环路里一个相干积分周期内的样本点数为N,为了能得到τ的极大似然估计,算得N个采样点信号rN=[r(0),r(1),r(2),…,r(N-1)]T关于τ和fd的联合条件概率密度函数:

p(τ,fd|rN)=

(2)

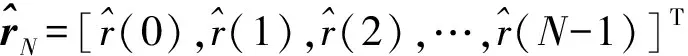
(3)

将式(3)展开、化简,可以得到τ和fd在非相干模式下的代价函数为:

(4)

式(4)考虑了载波的初相φ,但是因为∂L/∂φ=0,说明估计是独立于载波相位的。式(4)就是所要使用的在非相干模式下的极大似然代价函数。

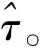
(5)

在式(5)中,具体各项如下所示:

(6)

(7)

其中d代表的是超前减滞后相关器的间距(一个码片)。

经分析可以得到:

(8)

综合式(5)～式(8),可得码相位估计偏差:

(9)

2.2 码鉴相值平滑滤波设计

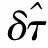
根据卫星导航接收机的原理,可以得到:

δρ=δτ·λcode

(10)

(11)

那么,假设用户在各个测量间隔内的速度保持不变,则可以利用下式进行滤波:

(12)

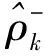
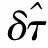
化简后的平滑公式如下式所示:

(13)

(14)

3 仿真实验验证

仿真试验结果如图3～图5所示。

图3 原跟踪环路结构中码鉴相误差

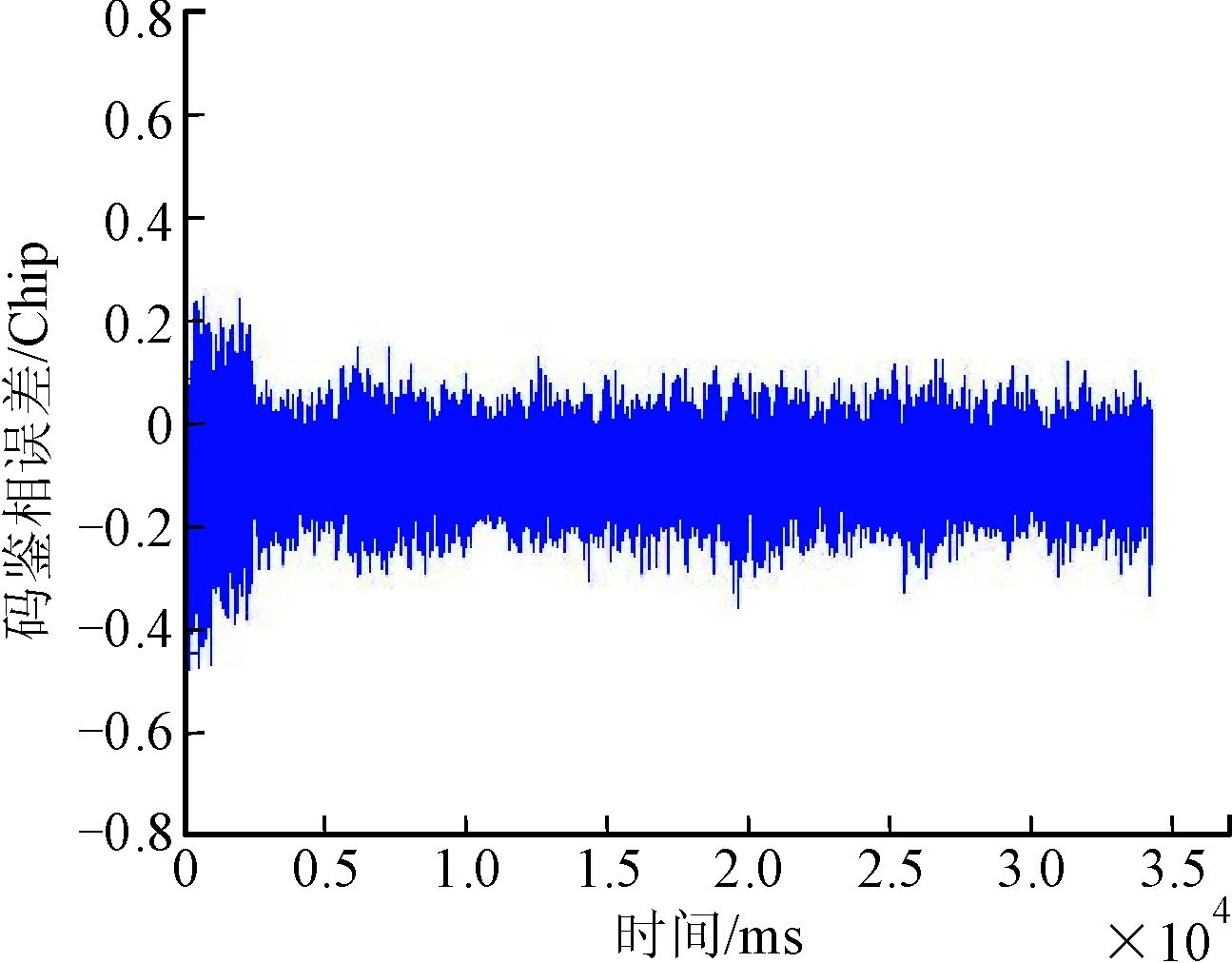
图4 基于极大似然估计法得到的码鉴相误差

图5 改进的基于极大似然估计法得到的码鉴相误差

由图3与图4所示仿真结果的比较,可以看出运用极大似然估计器以后,在基带环路实现跟踪的一小段时间之后,码鉴相结果开始变优,鉴相误差小于传统码环鉴相器的误差。

图5所示的仿真结果与图3、图4所示的结果比较,则可以发现,当码相位的极大似然估计值进行α滤波后,环路复制的码鉴相值进一步接近软件接收机实际接收信号的C/A码相位值,码鉴相误差显著减小。且改进以后,接收机基带解调信号变得更为顺畅了,改善了环路的稳定性。由上述观察可知,文中所述的改进方案有较好的实验效果,达到了预期目的。

4 分析和结论

1)极大似然估计法与传统码鉴相方法比较,具有一致性、无偏性和正则性,在估计性能上更有优势。采用的非相干模式下的代价函数,可以使估计值对载波相位不敏感。

2)文中提出的改进方法,在改造传统接收机码环结构,使用极大似然估计器的基础上,融合了α滤波器。实验结果表明,改进后的码鉴相算法,误差明显减少,估计精度增高,且改进后的接收机基带环路拥有更好的稳定性。

3)单纯卫星导航接收机的基带环路工作性能受到工作环境的极大制约。为进一步提高接收机环路的跟踪精度和稳定性,可以使用MEMS惯性器件来和接收机进行组合,对环路跟踪起到辅助作用。

参考文献:

[1] KAPLAN E D, HEGARTY C. Understanding GPS: principles and applications [M]. 2nd ed. London：Artech House, 2006: 25.

[2] GLEASON S, GEBREEGZIABHER D. GNSS应用与方法 [M]. 杨东凯, 樊江滨, 张波, 等，译. 北京: 电子工业出版社, 2011: 16.

[3] 秦峰. 基于矢量跟踪的高动态载体超紧组合导航技术研究 [D]. 上海: 上海交通大学, 2014.

[4] 谢钢. GPS原理与接收机设计 [M]. 北京: 电子工业出版社, 2009: 304.

[5] 同钊, 李兵兵, 惠永涛, 等. 短延迟多径干扰下的跟踪环路鉴别器设计 [J]. 西安电子科技大学学报(自然科学版), 2015, 42(5): 7-12.

[6] 张贤达. 现代信号处理 [M]. 北京: 清华大学出版社, 1995: 266.

[7] 程俊仁, 刘光斌, 张倩, 等. 基于极大似然估计器的GNSS矢量跟踪算法 [J]. 航空学报, 2014, 35(9): 2559-2567.

[8] WON J H, PANY T, EISSFELLER B. Noniterative filter-based maximum likelihood estimators for GNSS signal tracking [J]. IEEE Transactions on Aerospace & Electronic Systems, 2012, 48(2): 1100-1114.