临近空间高超声速滑翔弹弹道特性仿真

喻晨龙， 谭贤四， 曲智国， 谢 非， 李陆军

(1. 空军预警学院研究生管理大队， 湖北 武汉 430019； 2. 空军预警学院防空预警装备系， 湖北 武汉 430019； 3. 长江勘测规划设计研究院， 湖北 武汉 430019)

临近空间高超声速滑翔弹因其飞行速度快、巡航飞行高度高、突防能力强、打击距离远和可重复使用等特点而倍受青睐。当前，可能作为作战武器临近空间高超声速滑翔弹的主要有2类：一类是由火箭助推至大气层高空后，无动力再入大气层而长距离滑翔的升力式再入滑翔弹，典型的有HTV-2和AHW；一类是机载平台投放后，由吸气式超燃冲压发动机连续启停助推的乘波体滑翔弹，典型的有X-43A、X-51A[1-5]。相比于弹道导弹，临近空间升力式再入滑翔弹在气动外形、运行环境、飞行受力、控制方式、机动模式和运动描述等方面存在差异[6-10]，给雷达的搜索和跟踪带来了很大挑战。

临近空间高超声速滑翔弹的运动轨迹分为平衡滑翔和跳跃滑翔2种，其目标的运动状态和控制量决定着目标飞行时受到的气动力：当纵向上的气动升力与重力和离心力的合力为0时，轨迹处于平衡滑翔状态；当这一合力不为0时，轨迹处于跳跃状态[11-13]。CHEN等[14]对目标的平衡滑翔轨迹进行了深入分析，推导了无量纲下速度、航迹倾角和飞行高度等状态量之间的解析关系;李广华等[15]区分了平衡滑翔和跳跃滑翔，并基于平衡滑翔状态仿真分析了跳跃轨迹的运动参数变化规律。然而，上述文献未探讨初始运动状态和控制量的改变对运动轨迹的具体影响。鉴于此，笔者建立临近空间高超声速滑翔弹的运动模型，以升力式再入滑翔弹为对象进行对比仿真，分析控制量攻角/倾侧角的改变对运动状态的影响及目标处于不同初始运动状态时的弹道轨迹。

1 运动模型

1.1 参考坐标系

为了描述目标的运动过程和雷达的探测过程，定义3个相关坐标系：

1) 地心(Earth Center，EC)坐标系。坐标原点为地球球心，x轴在赤道平面内并指向本初子午线，z轴沿地轴并指向正北，y轴与x、z轴构成右手系。

2)飞行器直角(Vehicle East-North-Up，VENU)坐标系。坐标原点为滑翔弹的质心，x轴在滑翔弹所在当地水平面内并指向正东，y轴在滑翔弹所在当地水平面内并指向正北，z轴与x、y轴构成右手系。

3)雷达站直角(Radar East-North-Up, RENU)坐标系。坐标原点为雷达站的中心，x轴在雷达站所在当地水平面内并指向正东，y轴在雷达站所在当地水平面内并指向正北，z轴与x、y轴构成右手系。

1.2 三自由度运动模型

假设地球为均匀圆球，不考虑自转的影响，则滑翔弹在无动力滑翔过程中满足EC坐标系和VENU坐标系的三自由度运动方程[14-15]，即

(1)

(2)

式中：r(t)、χ(t)、ψ(t)分别为滑翔弹在EC坐标系下的地心距、经度和纬度;v(t)、γ(t)、ψ(t)分别为滑翔弹在VENU坐标系下的速度、航迹倾角和航向角；m为滑翔弹的质量；g为重力加速度；σ(t)为控制量倾侧角；D(t)、L(t)分别为飞行过程中所受阻力和升力,

(3)

(4)

其中CD(t)为阻力系数，CL(t)为升力系数，ρ(t)为大气密度，S为滑翔弹气动参考面积。

由文献[16-18]可知：当滑翔弹的速度>8 Ma时，升力系数可简化为攻角α(t)的线性函数，阻力系数可简化为α(t)的二次函数，对气动参数插值拟合后，可得

CD(t)=0.044+0.08α(t)+2.2α2(t),

(5)

CL(t)=-0.151 7+3.151α(t)。

(6)

通过滑翔弹的三自由度运动方程可知：滑翔弹的弹道取决于目标的控制量攻角α(t)、倾侧角σ(t)和目标的初始运动状态。

2 弹道分析

假设滑翔弹的气动参考面积为0.35 m2，质量为907 kg，热流密度、动压、过载的约束分别2 000 kW/m2、500 kPa和4g，最大升阻比为3.233 1，对应的攻角为11.6°。

2.1 控制量影响

再入条件中，初始运动状态的速度为20 Ma，飞行高度为80 km，航迹倾角为0°，航向角为0°，再入条件控制量见表1。当再入条件确定后，根据式(1)、(2)迭代得到目标在EC和VENU坐标系下的运动状态，以此分析控制量的影响，如图1所示。

表1 再入条件控制量

由图1(a)-(c)、(g)、(h)可以看出：弹道1-3的飞行高度、速度、加速度、航迹倾角、航迹倾角速度的变化曲线基本重合；弹道5的飞行高度最高，航迹倾角、航迹倾角速度最小，而弹道4的飞行高度最低，速度下降幅度和加速度振荡幅度最大，航迹倾角、航迹倾角速度最小，它们均呈周期性变化。上述结果表明：攻角决定着纵向平面的运动参数，包括飞行高度、速度、加速度、航迹倾角、航迹倾角速度，它们均呈周期性变化，其振荡幅度取决于攻角的大小；纵向平面始终存在强度较大的跳跃周期机动。

由图1(d)、(f)可以看出：弹道3-5的经度和航向角变化曲线基本重合，说明弹道飞行的经度和航向角维持不变；弹道1的经度偏移幅度最大，弹道2次之。由图1(e)可以看出：5条弹道的纬度变化曲线基本重合成一条直线，说明控制量攻角和倾侧角变化不影响纬度。上述结果表明：倾侧角决定着横向平面运动参数，包括经度、纬度、航向角，这些运动参数均呈线性变化，偏移幅度取决于倾侧角的大小，当且仅当倾侧角不为0°时，横向平面存在线性偏移机动。

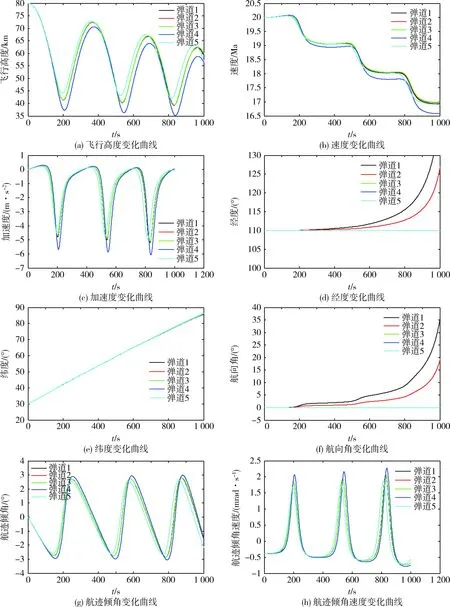
图1 控制量对弹道的影响

2.2 初始运动状态影响

初始运动状态影响滑翔弹受到的初始气动力，决定轨迹是处于平衡滑翔还是跳跃滑翔，以及跳跃的频次与幅度等。

2.2.1 航向角

作战时，RENU坐标系和VENU坐标系面朝东方，仿真时仍采用2.1中的再入条件，只是航向角变为90°。初始航向角改变对弹道的影响如图2所示。

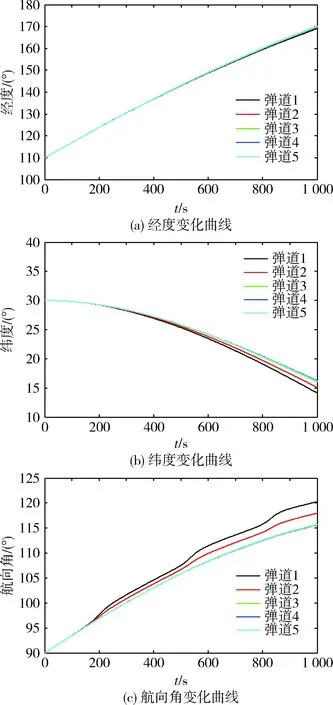
图2 初始航向角改变对弹道的影响

由图2(a)可以看出：5条弹道的经度变化曲线基本重合，且随时间呈线性变化。由图2(b)、(c)可以看出：弹道3-5的纬度和航向角变化曲线基本重合；5条弹道向赤道偏转，其中弹道1的偏转最大，弹道2次之。上述结果表明：当初始航向角改变时，由于地心引力的影响，横向偏移始终存在，甚至当倾侧角为0°时，目标不仅在纵向平面运动，还会发生横向偏移。

2.2.2 航迹倾角

假设4条弹道初始航迹倾角依次为5°、2°、0°、-5°，控制量攻角为最大升阻比的对应值11.6°,倾侧角为0°,飞行高度为60 km。初始航迹倾角改变对弹道的影响如图3所示。

由图3(a)可以看出：弹道1、4的初始航迹倾角数值相等、符号相反，从波谷到波峰的跳跃幅度相同，弹道1-4的初始航迹倾角数值递减，跳跃幅度递减；弹道1、2的初始航迹倾角为正，向上跳跃，弹道3、4的初始航迹倾角≤0°，向下跳跃；弹道1的飞行高度明显高于弹道2，且部分超过临近空间范围。上述结果表明：初始航迹倾角的数值决定跳跃幅度大小，正负决定最大飞行高度，当初值为正且大时，由于气动升力大，飞行高度会超过临近空间范围，航迹倾角初值应为小且不大于3°。

由图3(b)可以看出：4条弹道的速度均呈“先平缓再突然降低”变化趋势，以类似“下台阶”的方式不断减小，且初始航迹倾角的数值越大，变化幅度越大，当初始航迹倾角为0°时，速度变化最平缓。这与图3(c)中加速度的变化情况相互佐证。上述结果表明：初始航迹倾角的数值决定速度的“台阶”长度和高度，正负决定速度“下台阶”的时刻，当初值为负且大时，由于气动阻力大，“下台阶”最早且“台阶”最长。

由图3(d)可以看出：弹道1-4的航迹倾角以其初始值为振幅做周期性振荡，且初始航迹倾角数值越小，振幅越小。这与图3(e)中角速度变化情况相互佐证。这说明航迹倾角始终周期性变化，初值决定振幅。

2.2.3 飞行高度

假设3条弹道初始飞行高度分别为80、60、50 km，控制量攻角为最大升阻比的对应值11.6°,倾侧角为0°,航迹倾角为0°。初始飞行高度改变对弹道的影响如图4所示。

由图4(a)可以看出：弹道1的飞行高度最高且振荡幅度波动最大；弹道2的飞行高度适中，在临近空间发生平稳周期性振荡；弹道3的飞行高度最低，初始时轨迹向上跳跃，振荡幅度最小。这说明初始飞行高度决定跳跃幅度，当飞行高度初值过低时，由于气动升力大，目标将向上跳跃。

图3 初始航迹倾角改变对弹道的影响

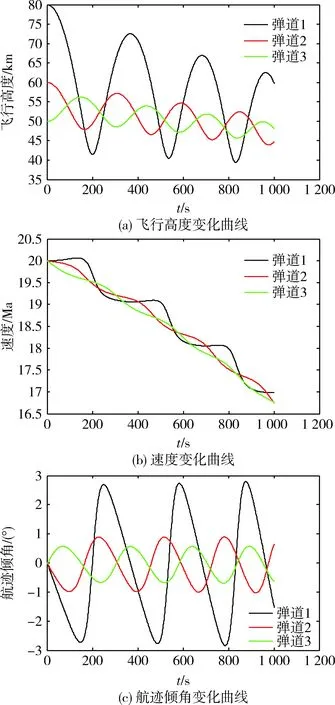
图4 初始飞行高度改变对弹道的影响

由图4(b)可以看出：弹道1的速度呈阶梯式下降；弹道2、3的速度呈近似线性下降。这说明初始飞行高度决定速度下降速度，当飞行高度初值较低时，大气密度大，由于气动阻力和气动升力大，目标速度迅速下降，无法维持“台阶”。

由图4(c)可以看出：弹道1在最高点处释放跳跃，航迹倾角在3°以内周期振荡，弹道2、3航迹倾角维持在1°以内周期振荡。这说明初始飞行高度决定航迹倾角的振荡幅度，当初始飞行高度初值低于60 km后，航迹倾角振荡幅度基本不变。

3 结论

临近空间高超声速滑翔弹的强机动运动给预警系统带来了巨大挑战，笔者深入分析了控制量攻角、倾侧角，运动参数航向角、航迹倾角、飞行高度的初值对弹道轨迹的影响。结果表明：控制量攻角和倾侧角分别决定着弹道的纵向和横向的运动轨迹，其中纵向为主要跳跃平面，当且仅当倾侧角不为0°时，轨迹才发生横向的线性偏移；弹道的初始航向角影响着弹道轨迹的横向偏移，而初始航迹倾角和初始飞行高度影响着跳跃轨迹。上述研究为下一步临近空间目标的探测与跟踪提供了依据。

参考文献：

[1] PAUL L M,VINCENT L R,LUAT T N,et al.NASA hypersonic fight demonstration overview,status,and future plans[J].Acta astronautica，2004,55(7):619-630.

[2] 李益翔.美国高超声速飞行器发展历程研究[D].哈尔滨： 哈尔滨工业大学,2016.

[3] STEVEN H W,JEFFREY S,DALE S,et al.The DAPPA/AF falcon program:the hypersonic technology vehicle #2(HTV-2) flight demonstration phase[C]∥15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference,28 April-1 May,2008,Dayton,Ohio,2008:2008-2539.

[4] RANDALL T V,LAERENCE D H,CHARLES R M,et al.X-43A Hypersonic vehicle technology development[J].Acta astronautica,2006(59):181-191.

[5] STEVEN W,MING T,SUE M,et al.Falcon HTV-3X-A reusable hypersonic test bed[C]∥15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference,28 April-1 May 2008,Dayton,Ohio:2008-2544.

[6] 秦雷，李君龙，周荻.国外临近空间高速滑翔弹头运动特征研究[J].战术导弹技术,2015,16(1):16-20.

[7] 李君龙，秦雷，谢晓瑛.临近空间非弹道式机动模式与跟踪滤波问题[J].现代防御技术,2017,45(1):99-106.

[8] 李慧峰.高超声速飞行器制导与控制技术[M].北京:中国宇航出版社,2012：10.

[9] 张毅，杨辉耀，李俊莉.弹道导弹弹道学[M].长沙：国防科技大学出版社,1999：3

[10] 李海林，吴德伟.高超声速临近空间飞行器非开普勒轨道研究[J].飞行力学,2012,30(3):276-279.

[11] 谢愈，刘鲁华，汤建国，等.高超声速滑翔飞行器摆动式机动突防弹道设计[J].航空学报，2011,32(12)：2174-2181.

[12] 王之，李慧峰，包为民.升力式再入飞行器体襟翼姿态控制方法[J].北京航空航天大学学报,2016,42(3):532-541.

[13] 谢愈，刘鲁华，汤建国，等.多约束条件下高超声速滑翔飞行器轨迹优化[J].宇航学报，2011,32(12)：2499-2504.

[14] CHEN X Q,HOU Z X,LIU J X,et al.Phugoid dynamic characteristic of hypersonic gliding vehicle[J].Science China(information sciences),2011(54):542-550.

[15] 李广华，张洪波，汤建国.高超声速滑翔飞行器典型弹道特性分析[J].宇航学报，2015,36(4):397-403.

[16] PHILIPS T H.A Common Aero Vehicle(CAV) model,description,and employment guide[R].USA:Schafer Corporation,2003.

[17] 赵汉元.飞行器再入动力学与制导[M].长沙:国防科技大学出版社,1997:197-220.

[18] 黄长强，国海峰，丁达理.高超声速滑翔飞行器轨迹优化与制导综述[J].宇航学报,2014,35(4):369-379.