一种基于理论弹道的安全管道生成算法

何攀登， 李 青， 陈雪涛， 胡彭辉

(1. 空军勤务学院航空弹药系， 江苏 徐州 221000； 2. 中国电子信息产业集团有限公司第六研究所， 北京 102209)

靶场试验中，为确保试验任务的顺利完成，必须对飞行导弹进行安全控制。试验前，根据导弹的飞行参数将理论弹道事先计算好，并保存在理论弹道文件中。该文件包含一系列理论轨迹点，这些轨迹点表明每一时刻飞行导弹所在的位置信息。理论安全管道(简称“安全管道”)是指导弹飞行弹道参数偏离设计值的容许变化范围，若超出该变化范围，则被认为是故障弹，应及时进行处理。告警安全管道是导弹正常动力飞行的边界线；炸毁安全管道是故障导弹必须终止动力飞行的边界线。导弹与安全管道上、下、左、右4个边界的距离是衡量导弹是否有效的关键参数，也是仿真模拟安全管道的主要依据[1-3]。

传统安全管道的制作都是人工在边界上取点，复杂度高且数据误差较大[4]。为了增加数据的实时性，减小误差，为试验指挥员提供更准确可靠的安控判决依据，笔者提出基于理论弹道的飞行导弹安全管道生成算法，并通过将其实际应用于某型导弹的安全管道生成验证该算法的有效性。

1 基本原理

1.1 地球坐标系转换为三维直角坐标系

理论轨迹点是地球坐标系下用角度制表示的经度和纬度，首先，将其转化为弧度制表示的经度和纬度；然后，根据

(1)

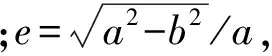
1.2 求轨迹点的单位法向量

根据文献[6-7]可知：理论轨迹由大量连续的点组成，且2点之间相差很小，因此可将2个相邻理论轨迹点A(x1,y1,z1)和B(x2,y2,z2)的三维直角坐标相减得到向量AB，单位化后近似作为每一个理论轨迹点在理论轨迹走向上的单位法向量n，如图1所示。

图1 单位法向量

1.3 求圆平面上的单位向量

利用向量叉乘的原理[8]，求取与n对应的圆平面上的2个单位向量a和b，如图2所示。

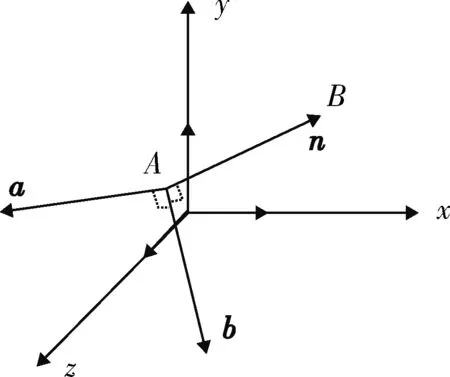
图2 向量叉乘示意图

根据图2可得，向量a和b可分别表示为

a=(axi,ayj,azk)，

(2)

b=(bxi,byj,bzk)，

(3)

则a和b叉乘可表示为

(4)

根据右手规则，向量n可表示为

n= (aybzi+axbzj+axbyk)-

(azbyi+axbzj+aybxk)。

(5)

同理，若已知任一理论轨迹点的坐标，则可根据1.2节求解出单位法向量，再利用向量叉乘原理求出轨迹点所在平面上的2个单位向量。具体算法流程如图3所示。

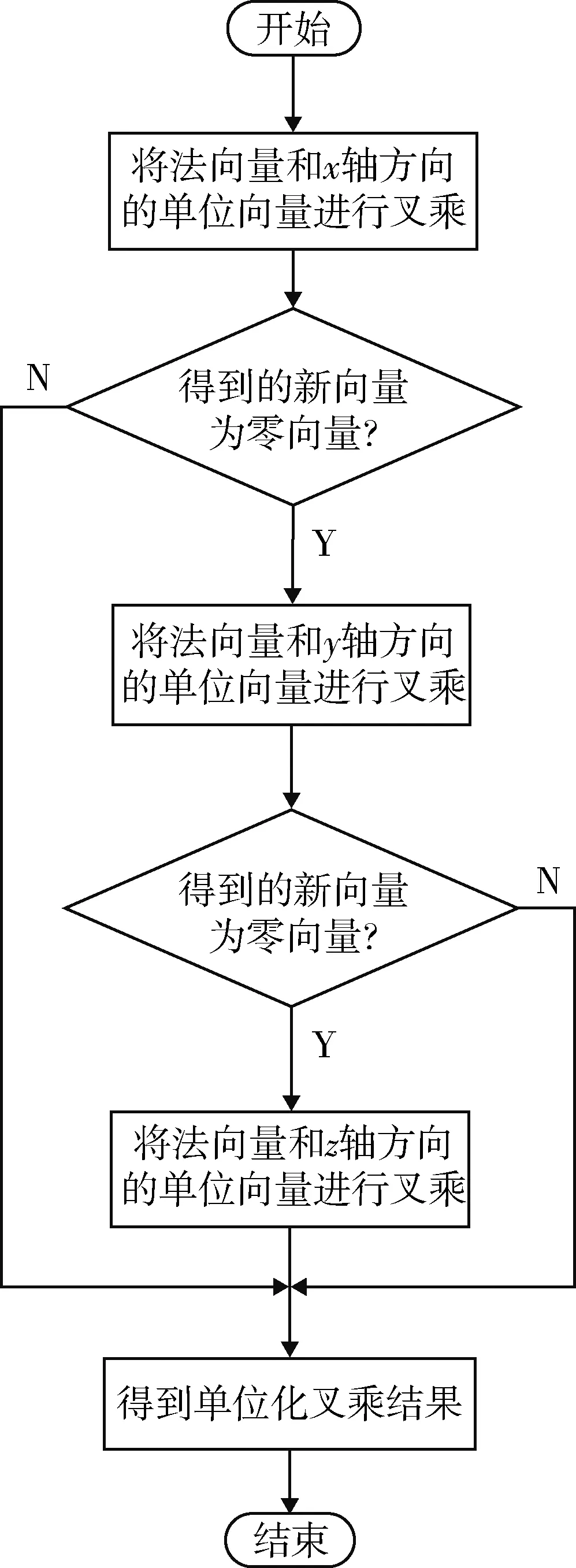
图3 求解理论轨迹点所在平面单位向量流程

1.4 生成安全管道

假定圆心C的单位坐标为(cx，cy，cz)，r为圆的半径，θ=[0，2π]，以向量n为法向量。三维空间中圆的参数方程示意图如图4所示。

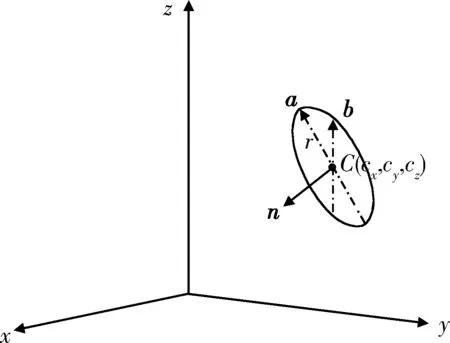
图4 圆的参数方程示意图

三维空间中圆的参数方程可表示为[9-10]

(6)

由式(6)可得：给定任意的θ值，即可求出圆上任意一点的坐标。

为了提高准确性，在每一个理论轨迹点所在的圆上求出36个点，即把每个圆36等分；其次，根据当前理论轨迹点与其对应安全管道上、下、左、右4个边界距离的平均值求得r；然后，根据读取的理论轨迹点数，对每一个理论轨迹点求出36个安全管道点，把这些生成的安全管道点保存到本地文件中；最后，使用三维地理信息引擎开发库osg和osgEarth，实现在三维地图上对导弹的理论轨迹和生成的安全管道的动态加载。一种基于理论弹道的安全管道生成算法流程如图5所示。

图5 一种基于理论弹道的安全管道生成算法流程

2 仿真验证

2.1 仿真试验

根据导弹理论弹道数据和人工采集的安全管道数据，使用Qt5.2.1、osg和osgEarth的开发环境，把理论轨迹点的集合和安全管道的上、下、左、右界作为仿真试验的数据源，生成某型号导弹安全管道。

将生成的导弹安全管道在三维地理信息引擎开发库osg和osgEarth中进行动态加载，仿真结果如图6所示。图中：黄色部分为以理论轨迹点为圆心，以理论轨迹点和人工采集后安全管道上、下、左、右4个边界距离的平均值503.204 m为半径，生成的导弹告警安全管道显示图；红色部分是以800 m为半径的导弹炸毁安全管道显示图。

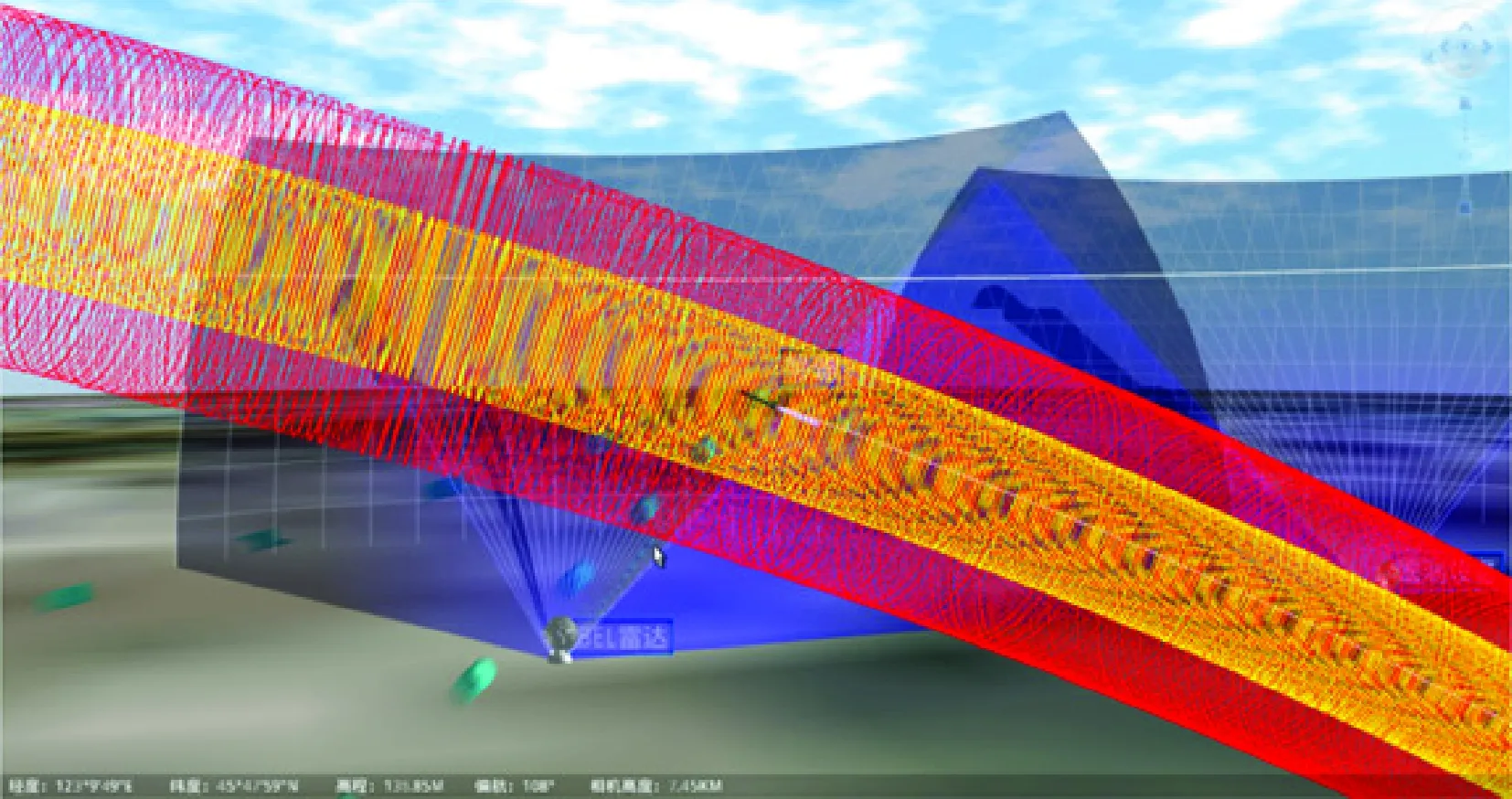
图6 生成的安全管道仿真结果显示图

将该算法生成的安全管道和人工采集的安全管道进行对比，如图7所示。图中：黄色为人工采集的安全管道，红色为该算法生成的安全管道。由图7可直观地看出：该算法生成的安全管道和安全管道非常接近。

图7 算法生成安全管道和人工采集的安全 管道仿真结果对比

2.2 仿真结果分析

为了对本文算法进行客观量化分析，对计算法生成的安全管道点和人工采集的安全管道点进行误差计算。由于安全管道由大量连续的点组成[11]，数据量很大，每一个数据点都有上、下、左、右4个边界值，因此随机选取第20个点和第50个点进行算法验证，结果如表1、2所示。

已知地球上任意2点用地球坐标系表示A1(L1,B1,H1)和A2(L2,B2,H2),用D12表示2点间的距离，Δ表示2点间的距离误差率，r1、r2分别表示点A1、A2到地心的距离，R=6378km，为地球半径,计算公式如下：

表1 第20个点的理论和人工采集安全管道的边界值

表2 第50个点的理论和人工采集安全管道的边界值

r1=R+H1，

(7)

r2=R+H2，

(8)

C= cosB1cosB2cos(L2-L1)+sinB1sinB2,

(9)

(10)

Δ=D12/503.24。

(11)

根据式(7)-(11)对该算法生成的安全管道点和人工采集的安全管道点进行误差计算，结果见表3、4。

由表3、4可以看出：该算法生成的安全管道上、下、左、右4个边界值误差率均小于0.35%，远小于实际靶场试验中允许的误差，几乎不会影响到指挥员的判断。上述结果表明：本文提出的算法能准确生成导弹飞行的安全管道，从而实现对靶场试验中飞行导弹的安全控制。

3 结论

笔者提出了一种基于理论弹道的飞行目标安全管道生成算法，该算法摒弃了传统安全管道制作采用人工采点的做法，可通过对理论弹道进行坐标转换、向量运算等操作自动生成安全管道。最后将该算法应用于某型号导弹飞行试验系统中，仿真结果表明：该算法精确度高，实现简单，具有很好的实际应用效果。在后续研究中，将再结合导弹的极限弹道、各种测控设备的误差以及安控时延等因素，以最大限度地发挥导弹飞行性能、缩小试验区域为目的优化安全管道。

参考文献：

[1] 孙艳英.—种关于目标与安全管道相对位置估算方法[J].海军航空工程学院学报,2014，29(4):307-308.

[2] 万树平.目标威胁评估的区间数方法[J].计算机工程与应用,2009,45(6):32-34.

[3] 杨得国,王明海,王立安.巡航导弹航迹与威胁区相对位置判定士法[J].四川兵工学报,2001,32(8):10-13.

[4] 孙艳英,沈怡.靶场试验安全管道设计与优化方法[J].兵工自动化,2014,34(11):79-93.

[5] 孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社，2001:36-37.

[6] 李宁波,雷虎民,谭诗利,等.基于虚拟域动态逆的空地反辐射导弹轨迹优化[J].弹道学报,2016,28(4):7-11.

[7] ZARCHAN P.Tractical and strategic missile guidence[M].New York:American Institute of Astronautics,2012：700-875.

[8] 方兴,方建勋,吴小欣.利用叉积判断法实现安全管道判断[J].战术导弹技术,2011(2):58-61.

[9] 罗志国.空间圆的参数方程及其应用[J].湖南师范大学学报(自然科学版)，2012,35(6):24-26.

[10] 刘宏义,肖瑜.基于高斯随机性的弹道轨迹仿真[J].电子科技,2012,25(12):37-38.

[11] BOX G E P,MULLER M E A.A note on the generation of random normal deviates[J].The annals of mathematical statistics,1958,9(2):610-611.