磁梯度张量系统发展及其误差校正研究现状

李青竹， 李志宁， 张英堂， 尹 刚， 范红波

(1. 陆军工程大学石家庄校区车辆与电气工程系， 河北 石家庄 050003； 2. 中国空气动力研究与发展中心高速所， 四川 绵阳 621000)

磁异常探测(Magnetic Anomaly Detection，MAD)技术可以对地下或水下小尺度磁性目标进行定位与识别[1]，不但可以探测水雷、地雷和潜艇等带有铁磁性材料的武器装备，还可以用于探测未爆弹，为实弹演习或训练中遗留未爆弹的排除提供数据支持。磁异常探测技术发展过程大致分为总场探测、梯度场探测及磁梯度张量场探测3个阶段[2]。相比总磁场强度、磁场矢量与磁矢量梯度测量，磁梯度张量测量[3]可提供更深度的磁场附加信息，不受定向误差的控制，对空间取向与旋转噪声相对不敏感；同时拥有更高的空间分辨率，不易受周围环境区域背景磁干扰与地磁日变影响。因而磁梯度张量探测技术被视为磁探测技术的下一次突破点[4]。国外研究者从20世纪70年代就已开展了磁梯度张量探测相关研究[5-6]，且已取得长足进展，而国内在理论研究、系统搭建及数据解释方面尚处于起步阶段。

磁梯度张量测量属于微弱磁异信号测量，对设备精度要求很高，作为磁性目标探测的基础，初始数据的准确性显得尤为关键，现有条件搭建的磁梯度张量系统并非理想校调，且捷联设备通常含有铁磁性物体，会对环境产生干扰磁场，从而影响测量结果。各种综合误差因素使得张量测量误差可达上千nT/m，因此必须对测量仪器进行校准并对载体进行磁干扰补偿。笔者从磁梯度张量系统的国内外研制现状出发，结合实际应用需求，以磁通门法差分磁梯度张量系统为主要研究对象，对其误差校正与载体磁干扰补偿相关研究成果进行综述，为未来我军发展高精度磁测仪器的校准工作提供参考。

1 磁梯度张量系统

磁梯度张量系统是磁梯度张量测量技术的实际应用基础，其测量误差直接决定了探测精度。磁梯度张量是磁场矢量在3个正交方向上的空间变化率[4]，在实际测量中以差分计算代替偏微分近似估计磁梯度张量各分量，故其对矢量(分量)磁力仪输出精度要求更高。

国内外研究团队在综合考虑磁传感器的灵敏度及其余相关参数(见表1)后，多采用超导效应和磁通门法搭建磁梯度张量系统。

表1 各类磁传感器的响应频率、测量范围及理论分辨率[7]

1.1 基于超导效应的磁梯度张量系统

利用超导量子干涉仪(Superconducting QUantum Interference Device, SQUID)阵列进行磁场分量测量，以构造磁梯度张量系统，可分为高温(77 K，使用液氮冷却)和低温(4 K，使用液氦冷却)2种。如：德国莱布尼茨光子技术研究所于1997年利用低温SQUID研制了Jessy Star张量系统[8]，及其空气动力学优化后灵敏度均方根噪声小于10 pT/m的Air Bird系统[9]；2000年澳大利亚联邦科学与工业研究组织(Commonwealth Scientific and Industrial Research Organization, CSIRO)基于高温SQUID研制了航磁梯度张量系统[10]，在低端数据流中以10 Hz频率对采样数据进行平衡后，其均方根噪声底线达到了2 pT/m以内；2008年美国橡树岭国家实验室(Oak Ridge National Laboratory, ORNL)研发了基于高温SQUID的航磁梯度张量系统[11]，其利用8个SQUID器件测量张量矩阵的9个分量。

近年来国内相关机构也开展了高温超导测量的研究工作，如：燕山大学与中科院物理研究所共同研制了高温超导量子干涉装置[12]，基于该装置设计了平面式梯度计[13]；吉林大学研制了高温超导磁梯度仪[14]并成功应用于地质勘探工作。但与世界先进水平相比还有较大差距。

超导量子干涉仪灵敏度极高但量程范围较小，其构建的磁梯度张量系统更适用于小范围微观工况(如生物磁测、金属无损探伤等)，且成本高，系统安装工艺与测量环境要求严格，不适用于我军现阶段对敌水下或地面磁性目标探测与地下未爆弹识别等宏观大范围测量工况。

1.2 基于磁通门法的磁梯度张量系统

磁通门法主要是利用磁通门传感器阵列测量各正交方向的磁场分量读数空间变化率，以代替磁梯度张量分量。以磁通门传感器构建的张量系统已经可以满足战场高精度定位与识别要求，其成本更低且安装要求更为简单，利于大批量生产制造。但是，磁通门传感器存在系统误差，因此必须进行输出校正。

2009年，澳大利亚CSIRO机构构建了四磁通门传感器阵列直角四面体张量系统，如图1所示，同方向上传感器间基线距离为0.6 m，该系统各张量分量测量点差异导致最终计算得到的张量矩阵存在结构误差。美国地质勘探局(United States Geological Survey, USGS)于2003年研制了如图2(a)所示的正四面体磁通门传感器张量系统并用于地质勘探[15]，其传感器基线距离为0.97 m，且外部安装了恒温装置以减少温度误差；该机构搭建的第二代平面十字形结构张量系统如图2(b)所示，基线距离为0.25 m，传感器放置在玻璃陶瓷的盒子里并用玻璃纤维平面固定，结构误差明显减小。美国海军水面作战中心(Naval Surface Warfare Center, NSWC)的2个研发小组也开展了相关研究，其中：以WIEGERT[16-17]为代表的小组研究了用于磁异定向的三角形张量系统和用于磁异目标定位的六面体张量系统，如图3(a)所示；以ALLEN[18]为代表的小组研制了用于水下磁异探测的十字形张量系统，如图3(b)所示，其中左上方的参考传感器用于其他3个磁传感器的误差校正。此外，新加坡、意大利等国科研机构相继研制了磁通门法三角形张量系统，用于水下磁性目标探测[19-20]，其中意大利科学院[20]研制的配备磁通门全磁张量梯度仪的地磁噪声水下无人机(Autonomous Underwater Vehicle,AUV)系统的测量分辨率可达到0.1 nT/m。

图1 CSIRO研制的直角四面体张量系统

图2 USGS研制的两代张量系统

图3 美国海军水面作战中心研制的张量系统

国内，哈尔滨工程大学于2010年开始张量系统数据解释理论研究[21]，并进行了最简磁通门张量系统配置论证;吉林大学全张量磁测技术实验室于2011年开始搭建张量系统[22]，于2012年研制出磁通门式球形反馈三分量全张量探头，并进行了飞艇探测汽车试验;国防科技大学于2012年利用DM-050型(德国产)高精度磁通门传感器搭建了平面十字形张量系统，并进行了张量系统的校正和补偿工作[23-24];原军械工程学院于2010年开始磁梯度张量相关理论研究，并于2012年搭建了磁通门法平面十字磁梯度张量系统，如图4所示，在此基础上进行了系统校正和补偿[25-26]，并逐步开展了磁性目标识别、定位和反演研究[27-29]。

图4 磁通门法平面十字磁梯度张量系统

2 磁通门式磁梯度张量系统误差分析

磁通门法磁梯度张量系统的测量误差由多种因素引起，这些误差源严重影响了磁梯度张量仪的测量精度，需要对系统进行校正并对载体、环境干扰场进行磁补偿。刘丽敏[30]对磁通门张量系统进行了结构、误差分析并以水下目标探测作为检测结果，明确提出了平面十字形结构具有结构误差最低、安装精度较高的优势；PANG等[31]对单个磁通门探头的系统误差进行了分析。结合前人观点，笔者认为磁梯度张量系统误差校正主要分为3部分：1) 传感器系统误差校正；2) 多传感器对准；3)磁干扰补偿。模块化误差后可利用矩阵理论对参数进行建模。

2.1 系统误差

由于制造技术和工艺水平限制，三轴磁通门传感器总会存在系统性误差，如：由轴位偏差、灵敏度标度因子和三轴非正交性等引起的张量分量误差可达数千nT/m。设传感器实际输出Br=(Brx,Bry,Brz)T，理想输出Bc=(Bcx,Bcy,Bcz)T，通过矩阵分析理论可分别建立三轴磁通门传感器的系统误差数学模型。

2.1.1 三轴零位偏差

理论上，理想无磁环境下，三轴磁通门传感器测量值应为0。但实际磁通门的铁芯中有剩磁，且存在电路漂移等问题，导致了传感器三分量输出不为0[32]，即存在零位输出偏差，其作用相当于传感器三轴偏置，设为I0=(ix,iy,iz)T，则有

Br=Bc+I0

。

(1)

2.1.2 三轴灵敏度标度因子

在理想情况下，当被测磁场满足三分量相等时，如果磁传感器三轴敏感元件灵敏度相同，则应测得相等的三分量输出;但由于传感器技术限制，往往三轴敏感元件不具有相同的灵敏度，从而导致各轴输出值出现差异[33]，笔者将磁场分量测得值与真实值之比定义为灵敏度标度因子。设标度因子cx、cy、cz表示各轴输出加权因子，则有

(2)

2.1.3 三轴非正交性

由于制造工艺限制，无法保证三轴磁通门传感器输出轴完全正交[34-35]。

非正交误差一般由非正交角表示。图5为一种三轴非正交角定义情况，图中：O-XYZ为标准参考坐标系；O-XrYrZr为传感器实际坐标系；O-XcYcZc为理想正交坐标系；O为坐标原点；OZc与OZr同轴，YrOZr与YcOZc共面。

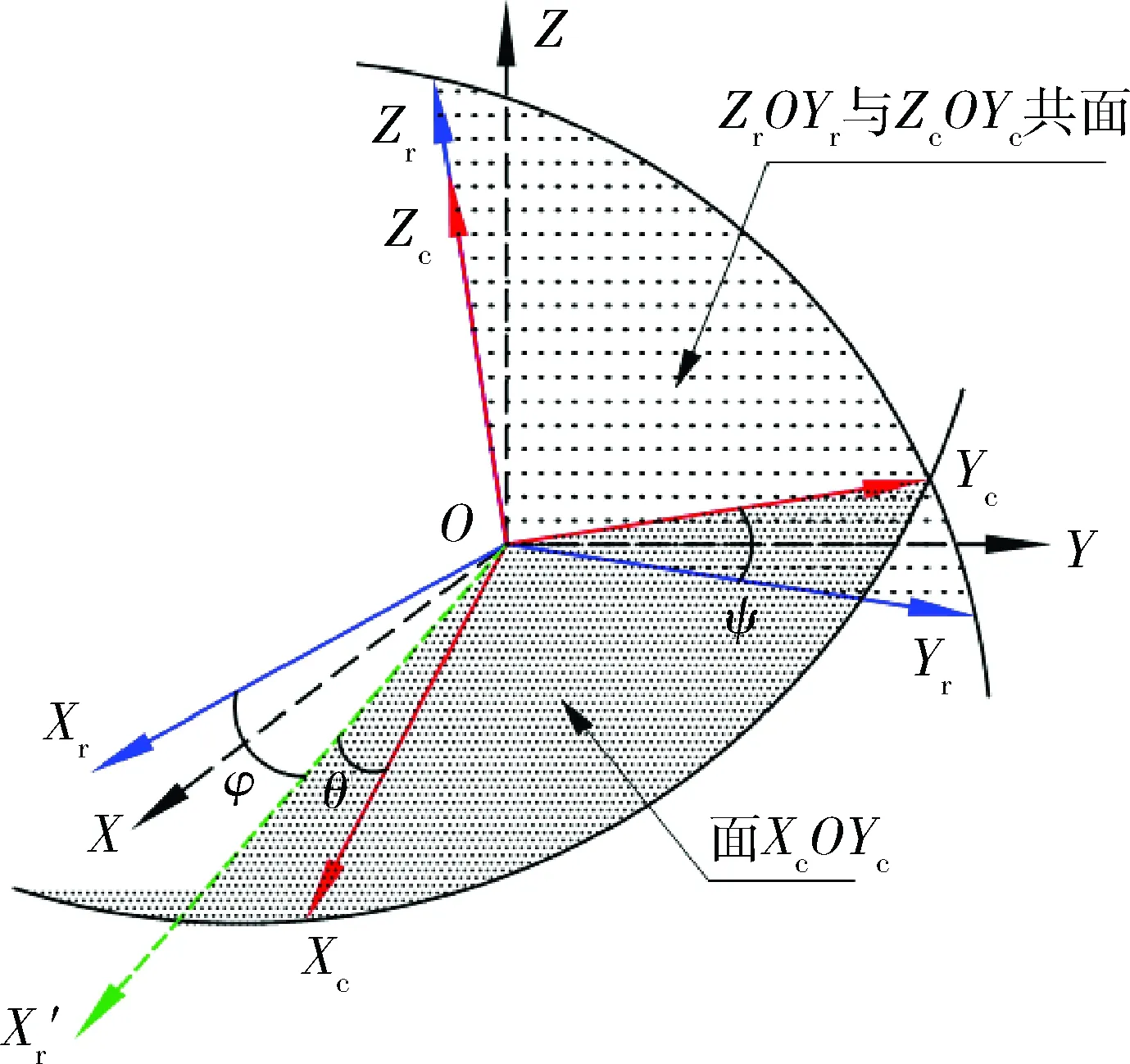
图5 一种磁通门传感器三轴非正交角示意图

设ψ为OYr与OYc轴间夹角，θ为OXr在XcOYc面内投影OXr′与OXc轴间夹角，φ为OXr与XcOXc面间夹角。对于确定的φ、θ、ψ，传感器理想正交系O-XcYcZc被唯一确定，可表示为

(3)

2.2 非对准误差

磁梯度张量系统通常由多磁通门传感器阵列设计而成，如正四面体、正六面体、平面正方形、三角形及平面十字形等结构形式，各传感器不同敏感轴排列安装过程存在配置结构(安装中心点偏移、偏转等)引起的位移、旋转非对准误差[29]。位移误差能够通过更高精度的制造工艺消除，而旋转误差则难以避免。

传感器输出轴朝向与固定外壳间本非一致对准，空间任意姿态两正交系间可通过包含3个非对准角度的旋转矩阵进行转换[36]。根据丹麦AUSTER等[37]提出的传感器绕轴采样校正策略，设对准前正交系为O-X1Y1Z1，对准后为O-XYZ，定义绕X轴旋转为横倾转换，绕Y轴旋转为俯仰转换，绕Z轴旋转为方位转换，则正交转换关系可由图6表示。

图6 传感器与平台正交坐标系转换示意图

图中：α、β、γ分别定义为横倾角、俯仰角和方位角。若仅考虑分别存在3种转换情况下，两正交系间坐标变换关系为

(4)

式中：Tα、Tβ、Tγ分别为横倾、俯仰和方位旋转矩阵。空间任意姿态的两正交系均能通过3个旋转矩阵相乘而进行转换。α、β、γ即建模而成的非对准误差。

2.3 磁干扰误差

运动载体(无人机、陆上平台及水下航行器等)材料多由铁磁性物质构成，载体在地磁场中会被磁化产生局部磁异常。此外，当载体中大量电子设备工作时，载体姿态或工作状态的变化也会产生时变磁异常，产生的环境磁场和目标磁异常场叠加会严重影响测量结果[38-40]。干扰场可分为固有磁场、感应磁场、涡流磁场和机载电气设备电磁干扰场[41]，分别对应于硬磁干扰、软磁干扰、涡磁干扰、电机干扰及电气设备产生的综合磁噪。

2.3.1 硬磁干扰

此类干扰由硬磁材料引起，硬磁材料的特点是矫顽力大，具有与永久磁体相似明显的磁滞特性，产生的磁感应强度不随载体位置或姿态改变而改变，称为固有磁场，相当于给各传感器矢量输出增加一个常值偏置。根据Tolles-Lawson方程[42]，固有磁场产生硬磁干扰Bh，其模型表示为

(5)

2.3.2 软磁干扰

此类干扰由软磁材料引起，软磁材料容易被外界磁场磁化，当外磁场消失后，所保留的剩磁也较小，其产生的感应磁场随载体姿态和地磁场的改变而改变，大小和方向与环境磁场大小、方向及铁磁性材料磁化特性有关，其作用相当于对磁场分量进行3阶系数矩阵加权[43]。感应磁场产生软磁干扰Bs，其模型表示为

(6)

式中：S为软磁系数矩阵；Bc为理想环境磁矢量场。

2.3.3 涡磁干扰

此类干扰由载体上金属片或金属壳等软磁材料切割地磁场产生，其大小和方向与地磁场梯度、载体运动加速度及运动随时间的变化率有关[44]。

2.3.4 电机干扰

此类干扰指测量过程中电动机产生的高频交变磁干扰。随着电机的工作状态改变,其幅值与频率均会发生变化，主要包括电机运转过程的高频交变磁场和电机设备中等效电流在其周围产生的磁场。

2.3.5 综合磁噪

此类干扰主要是指由机载电气设备产生的电磁干扰与数据采集过程中产生的测量噪声等。

2.4 温度、磁芯磁滞系数及测量噪声

2.4.1 温度系数

由于温度敏感性机制复杂，且取决于传感器类型，故有必要研究磁通门传感器温度特性，进而补偿温度漂移。在温度补偿方面，一些研究者对磁通门传感器温度特性进行了分析、测试或采用硬件进行补偿[45-46]；PANG等[47]使用支持向量机对磁通门传感器温差、非线性度漂移进行补偿，有效提高了测量精度。但因无法保证磁场与传感器轴方向一致，因而难以分别进行刻度因子和零偏温度特性测试；另外，由于温度误差非线性明显，故难以建立准确的数学模型。

2.4.2 磁滞

相关研究发现磁滞主要导致磁传感器非线性误差，一些研究者进行了深入分析：JANOSEK等[48]发现磁滞与交叉场效应会引起磁传感器非线性误差； BRAUER等[49]计算了由横场效应引起的磁通门传感器非线性；GORDON等[50]利用简化线性磁滞模型进行了灵敏度分析；MARSHALL[51]提出了一种多项式非线性磁滞模型；PRIMDAHL[52]对实际磁滞曲线进行了理论分析；BRAUER等[53]构建了由2～5阶系数构成的非线性拟合模型；VUILLERMET等[54]提出了以非线性方法预测微磁通门传感器输出；GEILER等[55]建立了磁通门传感器非线性响应定量模型。然而，目前仅是对三轴磁传感器进行非线性测试或分析，针对非线性误差校正的研究较少。笔者认为:磁芯磁滞回线作用于磁化与退磁过程[56]，不受外场幅值畸变影响，磁芯磁化后输出幅值稳定，对于无磁极倒转的稳定磁场环境，磁滞现象仅产生剩磁并表现为零偏，磁滞回线对测量影响较小。

2.4.3 测量噪声

噪声在任何测量中均存在，磁传感器本身存在噪声，与器件本身有关，需对选用的传感器进行噪声测试与评估。另外，实验环境中不可避免存在环境噪声，导致测量值波动，波动大小与采样率有关，需要进行分析。机载电子设备产生的电磁干扰也属于测量噪声范围。

3 磁梯度张量系统校正方法

3.1 针对单磁通门传感器的校正方法

磁通门式磁梯度张量系统由多磁通门探头阵列组成，因此单独对磁通门传感器进行校正可直接提升张量系统测量精度。

现有校正算法大多以传感器绕轴采样校正策略为基础，通过无磁平台(如捷克PETRUCHA等[57]构建的三轴旋转铝合金平台)对矢量磁强计绕轴采样，从而较为方便地提取空间各姿态的传感器输出数据。校正方法可分为直接校正和间接校正2种。

1) 直接校正法

通过理想和实际测量数据进行误差参数建模，利用相关数学工具直接计算出具体误差参数，并以此校正传感器输出，目前较为成熟的有线性和非线性最小二乘估计算法、递归拟合算法和高斯-牛顿迭代法等。丹麦MERAYO等[58]利用线性最小二乘法计算了磁传感器参数；芬兰PYLVANAINEN[59]提出了递归拟合算法，以自适应更新传感器校正参数；美国ALONSO等[60]提出了2步批处理方法，第1步产生较好的初始校正参数，第2步采用高斯-牛顿迭代法估计零偏、标度因子和非正交角。国内针对最小二乘估计算法已有较成熟理论：黄琳等[61]进行了近地卫星姿态确定与磁传感器在线校正的组合参数估计；PANG等[23]构建了系统误差和外界铁磁元素干扰集成参数模型，并使用矢量校正方法补偿张量系统输出，利用大量姿态数据进行非线性拟合以估计所有参数，但需测得较精准的标准矢量输出作参考；YIN等[25]使用2个非线性转换构建单传感器系统误差线性方程组，以估计出具体参数值，由于未进行任何数学简化，在外界磁干扰较小的情况下校正精度很高，且由于采用标量校正，成本大大降低。以上算法均以直接估计传感器具体系统误差参数为目标，称为直接校正法。

2) 间接校正法

不计算传感器具体误差参数，而是利用卡尔曼滤波、神经网络等信号处理方法对输出进行理想化校正(一般仅限于总场数据),或通过椭球拟合等方法间接求得替换校正参数。如：美国CRASSIDIS等[62]对比了顺序中心、扩展卡尔曼滤波(Extended Kalman Filter, EKF)和无迹卡尔曼滤波(Unscented Kalman Filter, UKF)算法，其中UKF算法对磁传感器校正性能更佳。国内，吴德会等[63]利用神经网络抑制了磁传感器绕某轴旋转时的总场强度误差；张晓明等[64]提出了基于椭圆约束的载体磁场标定补偿技术，利用求得的间接椭球系数对测量数据进行理想化校正；文献[65-66]作者对其进行了拓展，使用椭球拟合法对三轴陀螺仪、电子罗盘进行快速标定；石岗等[67]利用椭球面方程系数提出了航测系统中磁传感器误差参数求解的2步标定法。这种不直接在误差机理上求得误差参数的方法，称为间接校正法。

笔者认为，直接和间接方法均能对传感器进行较为精确的校正，但2种方法各有利弊:直接校正法的测量环境相对更为严格，计算机理更复杂，环境磁干扰等不确定因素会影响校正结果，但由于可直接求得传感器系统误差的具体参数值，且传感器自身系统误差不易因外界测量环境而改变，因此校正结果具有较高的鲁棒性，参数可对不同测量数据重复使用；而间接校正法法更倾向于复杂测量环境的当次快速校正，且校正能达到较高精度，但由于不能直接求得传感器系统误差参数值，每一次得到的测量数据均需进行替换参数获取或进行信号处理。

3.2 针对多传感器阵列的对准方法

当各传感器已被校正到较理想状态，各自来看传感器三轴输出是正交的，但若将所有传感器置于同一参考系下，各自输出朝向却是错乱的。目前对磁传感器或加速度计阵列的非对准误差校正，主要是通过数学建模进行非对准参数估计。

哈尔滨工程大学黄玉等[68]分析了安装错位、三轴指向偏差等因素，分析对比了十字形传感器阵列的2种放置方式。差分法张量测量只需求得该点传感器阵列磁场分量读数差值，对磁场矢量朝向并无要求。以平面十字形阵列为例，用图7表示其传感器阵列的对准思路[69]，以其中一个传感器为参考标准校准非对准误差的方法，不用考虑参考平台框架输出方向，尝试将传感器输出B2、B3、B4向B1对准。

图7 张量系统非对准误差校正示意图

现有非对准误差校准技术主要有以下几种：

1) 光学校准法

采用正六面体光学棱镜和正交光学系统校正非对准误差，该方法要求对光学系统和光学棱镜初始坐标系高精度校调。如:德国汉堡国防军大学采用激光干涉仪对3D亥姆霍兹线圈正交度进行了校正，而后转动磁通门传感器计算出非正交误差和非对准误差参数[70]；美国纽约大学等机构采用3D亥姆霍兹线圈配合光学仪器校正了霍尔传感器阵列[71]。

2) 旋转对准法

需结合无磁转台进行三轴旋转采样，利用构建的线性误差模型估计非对准误差，该方法对转台放置与转角精度要求较高，且需要各传感器三轴输出为正交。如：笔者[26]为校正平面十字磁梯度张量系统，将系统固定在三轴旋转平台上，以不同的垂线角度绕Z轴旋转，从而获得较丰富的姿态数据；PANG等[69]同样将磁传感器阵列固定在无磁旋转装置上进行绕X和Z轴旋转采样，以对准传感器输出。

3) 地磁参考法

该方法需借助全球定位系统(Global Positioning System,GPS)航向角信息和当地磁偏角信息，通过飞行器搭载的磁传感器阵列进行固定航向的航磁数据采集，从而以环境地磁数据为参考进行非对准参数的标定。如：北京航天航空大学吴永亮等[72]提出了圆约束非对准误差估计算法，以校正传感器间非对准误差，就是利用航磁数据对捷联磁测仪器进行校准。

4) 多维度机器人校准法

采用六自由度机器人校正非对准误差，但需要精确控制姿态，且操作复杂[73]。

磁梯度张量系统一般由科研人员自行安装构建，非对准误差在传感器安装固定之后不会随测量环境变化而改变。考虑校正成本与常规测量条件限制，在较为普遍的地面静态校准过程中，相较其他方法，旋转对准法更为方便且易于实现，校正成本更低。此外，旋转对准法可同时进行传感器系统误差校正的数据采集，从而实现系统一体化校正。

4 载体磁干扰补偿技术

载体磁干扰补偿研究一直以来是许多从事全张量磁梯度系统开发与应用的军方与研究机构关注的问题。目前，单矢量传感器的补偿方法较为成熟，现有技术主要针对磁总场和分量场进行补偿，其补偿方法又分为被动补偿和主动补偿2种。

1) 被动补偿

通常称为“硬补偿”。此方法采用外加固定磁铁、3D亥姆霍兹线圈、坡膜合金和导电板等辅助设备进行补偿，但其工作方法复杂，成本也较高。如：美国水面作战中心2004年前后开展的水下无人航行器全张量磁梯度系统的磁干扰补偿研究，将参考磁力仪测得的磁场值转化为电流值加载到其他传感器外的3D亥姆霍兹线圈上，以此来消除载体磁干扰[74-76]。

2) 主动补偿

通常称为“软补偿”。此方法通过建立载体磁场数学模型，由计算机实时计算出干扰大小并加以去除，从而达到补偿的目的。这种方法仅需根据现有环境下的干扰机理进行补偿数学建模，从而对测量数据进行后期处理以消除干扰磁场影响，且可以利用存储在计算机中的补偿参数对载体磁场进行实时补偿，由于不需要外加辅助设备，因而补偿成本低，补偿效率高。如：于振涛等[77]在硬磁和软磁干扰的基础上，建立了四面体磁梯度张量系统载体磁干扰的数学模型和补偿算法，能有效辨识补偿参数；龙礼等[78]根据最小二乘椭球拟合思想，提出了一种基于最大似然估计的椭球拟合补偿算法，并利用牛顿优化法获得误差补偿参数，输出精度较高；国防科技大学研究者[73,79]对载体干扰磁场的特性、基于线性测量模型的载体干扰磁场补偿方法、基于非线性模型的载体干扰磁场补偿方法等问题进行了研究，并通过实际装备的搭载试验对所提方法进行了验证；YIN等[25]利用正方形铁块和圆盘形磁铁模拟载体的硬磁和软磁干扰，在充分考虑到磁场测量时载体姿态变化均匀性的条件下，进行了自身误差的一体化校正；张光等[80]提出了一种针对磁张量系统载体一体化线性磁张量补偿方法，结合固有磁场影响和感应磁场影响建立了载体磁张量场补偿模型，求解补偿，系数直接对张量分量进行补偿且补偿性能良好。这些算法均是基于Tolles-Lawson方程，针对固有磁场、感应磁场作为主要干扰源进行的参数建模。

笔者认为：硬补偿方法成本高，对设备要求更加严格，更适用于特定环境(如密封的固定磁场环境或需严格排除干扰的磁试验机房)下的高精度补偿；而软补偿方法更具实用性，但补偿模型过于单一，且Tolles-Lawson方程不能适用于所有复杂测量环境，针对载体中复杂的涡磁干扰、电机干扰及载体工作状态变化及姿态变化等造成的磁场干扰也无法进行详细描述。对传感器阵列而言，多矢量磁传感器间也因存在相互作用而产生测量噪声。若能以多角度、更复杂的干扰机理建立更全面的补偿模型，则更有利于提高磁梯度张量系统的测量。如：杨云涛[81]利用信号处理等方式对测量信号进行处理，针对载体上电机产生的磁场噪声，提出了小波-参数补偿降噪算法，建立了消除电机交变磁扰和等效电流磁扰补偿模型；王维[82]针对载体多电气设备产生的综合磁场噪声，提出了基于EMD-形态滤波降噪算法和对各个IMF分量的最佳滤波层数算法，该方法能较好地消除高频交变和脉冲类磁场噪声，但仅能分析总场测量数据。

5 研究展望

高精度磁梯度张量场测量是未来地磁导航、矿藏勘探、铁磁目标探测与寻雷反潜、登月探月工程等研究领域的重要突破点。针对特定磁梯度张量系统进行专业深度误差校正，提供动载磁梯度张量测量误差校正与干扰磁场补偿的配套思路和快速有效的方法，对我军目前的军事战略需要以及科研与工程实际具有重要意义。随着磁传感器技术、航磁理论研究的不断深入，基于磁梯度张量系统的系统误差与载体磁干扰补偿技术取得了大量的成果，展望基于复杂磁测环境下的全张量磁梯度场测量的未来研究方向，笔者认为应从以下方面加强研究：

1) 目前对单磁传感器系统误差考虑还不够全面，现有校正手段未考虑对温度误差、非线性误差进行传感器三分量输出一体化校正，且校正精度受限于目前传感器自身精度与校正算法，未来可考虑更完备的误差模型建立方法和一体化参数构建。

2) 多传感器阵列的非对准误差虽然模型建立较为完备，但由于设备校正环境的限制，对校正平台校调精度要求较高，后期可考虑更合理的张量磁传感器阵列结构布局、更先进的校正策略和算法，从而有效消除非对准误差。

3) 现有载体磁干扰补偿模型大多主要考虑软、硬磁干扰与传感器系统误差模型相结合的补偿方式，后期可进行涡流磁场与电机干扰磁场量化建模，并引入现有补偿模型进行磁传感器与张量系统的多角度一体化补偿校正。

4) 为进一步提高磁梯度张量系统校正精度与真实性，后期可选择更为理想的匀强场环境，选用更先进、更高精度的传感器，并结合分量场在张量场理论级别上研发更先进的降噪技术，以消除机载中真实存在的电气设备、电机等电磁干扰。

参考文献：

[1] 卞光浪.顾及地磁背景场的多目标磁异常分量换算方法[J].武汉大学学报, 2011,36(8):914-919.

[2] 张昌达.关于磁异常探测的若干问题[J].工程地球物理学报,2007,4(6):549-553.

[3] 张昌达.航空磁力梯度张量测量：航空磁测技术的最新进展[J].工程地球物理学报,2006,3(5):354-361.

[4] SCHMIDT P,CLARK D,LESLIE K,et al.GETMAG ? a SQUID magnetic tensor gradiometer for mineral and oil exploration[J].Exploration geophysics,2004,35(4):297-305.

[5] WYNN W M.Dipole tracking with a gradiometer[R].Washington,DC,US：Naval Ship Research and Development Laboratory Informal Report NSRDL/PC,1972：3493.

[6] WYNN W M,FRAHM C P,Carroll P J,et al.Advanced super-conducting gradiometer/magnetometer arrays and a novel signal processing technique[J].IEEE transactions on magnetics,1975,11:701-707.

[7] 张昌达.若干物探技术的最新进展[J].工程地球物理学报,2012,9(4):406-412.

[8] ARGAST D,FITZ G D,HOLSTEIN H,et al.Compensation of the full magnetic tensor gradient signal[C]∥Proceedings of ASEG 2010.2010:1-4.

[9] CHWALA A,STOLZ R,ZAKOSARENKO V,et al.Full tensor SQUID gradiometer for airborne exploration[C]∥ Proceedings of 22nd International Geophysical Conference and Exhibition.2012.

[10] KEENAN S T,CLARK D,BLAY K R,et al.Calibration and testing of a HTS tensor gradiometer for underwater UXO detection[C]∥Proceedings of 2011 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices.2011.

[11] GAMEY T J.Development and evaluation of an airborne superconducting quantum interference device-based magnetic gradio-meter tensor system for detection,characterization and mapping of unexploded ordnance[R].Oak Ridge,US:Battelle Memorial Inst Oak Ridge TN,2008.

[12] 漆汉宏,田永君,王天生.高温超导双晶结垫圈型dc SQUID磁强计的研制[J].电子器件,2003,26(4):333-336.

[13] 郎佩琳,陈珂,郑东宁.高阶高温超导量子干涉器件平面式梯度计的设计[J].物理学报,2004,53(10):3530-3534.

[14] 赵静.高温超导磁梯度仪关键技术研究[D].长春：吉林大学,2011.

[15] ROBERT E B,SMITH D V.BROWN P J.Calibrating a tensor magnetic gradiometer using spin data[R].Reston,VA,US：Geological Survey,2005.

[16] WIEGERT R,PRICE B,HYDER J.Magnetic anomaly sensing system for mine countermeasures using high mobility autonomous sensing platforms[C]∥Proceedings of OCEANS 2002 MTS/IEEE.2002:937-944.

[17] WIEGERT R.Man-portable magnetic scalar triangulation and ranging system for detection,localization and discrimination of UXO[C]∥Proceedings of OCEANS 2009 MTS/IEEE.2009.

[18] ALLEN G I,SULZBERGER G,BONO J T,et al.Initial evaluation of the new real-time tracking gradiometer designed for small unmanned underwater vehicles[C]∥Proceedings of OCEANS 2005 MTS/IEEE.2005:1956-1962.

[19] PEI Y H,YEO H G,KANG X Y,et al.Magnetic gradiometer on an AUV for buried object detection[C]∥Proceedings of OCEANS 2010 MTS/IEEE.2010:1-8.

[20] COCCHI L,CARMISCIANO C,PALANGIO P,et al.S3MAG:low magnetic noise AUV for multipurpose investigations [C]∥Proceedings of OCEANS 2015 MTS/IEEE.2015:1-3.

[21] HUANG Y,SUN F,WU L.Synchronous correction of two three-axis magnetometers using FLANN[J].Sensors and actuators A:physical,2012,179:312-318.

[22] 李光.基于磁通门的航空磁梯度张量系统研究[D].长春：吉林大学,2013.

[23] PANG H F,PAN M,WAN C,et al.Integrated compensation of magnetometer array magnetic distortion field and improvement of magnetic object localization[J].IEEE transactions on geoscience and remote sensing,2014,52(9):5670-5676.

[24] PANG H F,LI J,CHEN D,et al.Calibration of three-axis fluxgate magnetometers with nonlinear least square method[J].Measurement journal of the international measurement confederation,2013,46(4):1600-1606.

[25] YIN G,ZHANG Y,FAN H,et al.One-step calibration of magne-tic gradient tensor system with nonlinear least square method[J].Sensors and actuators A,2015,229:77-85.

[26] 李青竹,李志宁,张英堂,等.平面十字磁梯度张量系统的两步线性校正[J].仪器仪表学报,2017,38(9):2232-2242.

[27] YIN G,ZHANG Y,FAN H,et al.Detection,localization and classification of multiple dipole-like magnetic sources using magnetic gradient tensor data[J].Journal of applied geophysics,2016,128:131-139.

[28] 尹刚,张英堂,米松林,等.基于倾斜角和Helbig方法的多磁源目标反演技术[J].上海交通大学学报,2017,51(5):577-584.

[29] LI J,ZHANG Y T,YIN G,et al.An approach for estimating the magnetization direction of magnetic anomalies[J].Journal of applied geophysics,2017,137:1-7.

[30] 刘丽敏.磁通门张量的结构设计、误差分析及水下目标探测[D].长春：吉林大学,2012.

[31] PANG H F,ZHANG Q,WANG W,et al.Calibration of three-axis magnetometers with differential evolution algorithm[J].Journal of magnetism and magnetic materials,2013,346(10):5-10.

[32] 洪咸东.基于正交三轴磁传感器测量误差讨论[J].测量与设备，2006(12):17-20.

[33] 邵英秋,程德福,王言章,等.高灵敏度感应式磁传感器的研究[J].仪器仪表学报,2012,33(2):349-355.

[34] 杨云,于晓东.三轴传感器非正交性误差分析及测量方法研究[J].水雷战与舰船防护,2009,17(1):53-55.

[35] 高翔,严胜刚,李斌.三轴磁通门磁梯度仪转向差校正方法研究[J].仪器仪表学报,2016,37(6):1226-1232.

[36] 李翔,王勇军,李智.航姿系统矢量传感器非对准误差及其校正[J].传感技术学报,2017,30(2):266-271.

[37] AUSTER H U,FORNACON K H,GEORGESCU E,et al.Calibration of flux-gate magnetometers using relative motion[J].Mea-surement science and technology,2002,13:1124-1131.

[38] 于振涛,吕俊伟,稽绍康.基于椭球约束的载体三维磁场补偿方法[J].哈尔滨工程大学学报,2014,35 (6):731-734.

[39] 赵建扬,林春生,贾文抖,等.直升机平台背景磁干扰建模与求解[J].华中科技大学学报(自然科学版),2016,44(2):21-25.

[40] 王婕,郭子祺,刘建英.固定翼无人机航磁探测系统的磁补偿模型分析[J].航空学报,2016,37(11):3435-3443.

[41] 赵建扬,林春生,贾文抖,等.直升机平台背景磁干扰建模与求解[J].华中科技大学学报(自然科学版),2016,44(2):21-25.

[42] Tolles W E.Magnetic field compensation system：US 2706801 A[P].1955-04-19.

[43] 张晓明,赵剡.一种快速载体磁场补偿方法研究[J].中北大学学报(自然科学版),2009,30(3):286-291.

[44] 王一凡.面向机载地磁测量的磁干扰补偿技术研究[D].武汉：华中科技大学,2012.

[45] PRIMDAHL F.Temperature compensation of fluxgate magnetometers [J].IEEE transactions on magnetics,1970,6(4):819-822.

[46] NISHIO Y,TOHYAMA F,ONISHI N.The sensor temperature characteristics of a fluxgate magnetometer by a wide-range temperature test for a Mercury exploration satellite[J].Measurement science and technology,2007,18:2721-2730.

[47] PANG H F,CHEN D,PAN M,et al.Nonlinear temperature compensation of fluxgate magnetometers with a least-squares support vector machine[J].Measurement science and technology,2012,23(2):025008.

[48] JANOSEK M,BUTTA M,RIPKA P.Two sources of cross-field error in racetrack fluxgate[J].Journal applied physics,2010,107(09E713)：1-3.

[49] BRAUER P,MERAYO J,NIELSEN O,et al.Transverse field effect in fluxgate sensors[J].Sensors and actuators A,1997,59:70-74.

[50] GORDON D,LUDSTEN R,CHIARODO R.Factors affecting the sensitivity of gamma-level ring-core magnetometers[J].IEEE transaction on magnetics,1965,1(4):330-337.

[51] MARSHALL S.An analytic model for the fluxgate magnetometer[J].IEEE transaction on magnetics,1967,3(3):459-463.

[52] PRIMDAHL F.The fluxgate mechanism：part 1 the gating curves of parallel and orthogonal fluxgates[J].IEEE transaction on magnetics,1970,6(2):376-383.

[53] BRAUER P,RISBO T,MERAYO J,et al.Fluxgate sensor for the vector magnetometer on board the “Astrid-2” satellite[J].Sensors and actuators A,2000,81:184-188.

[54] VUILLERMET Y,AUDOIN M,CUCHE R.Application of a non-linear method of moments to predict microfluxgates output[J].Sensors and actuators A,2010,158:212-216.

[55] GEILER A L,HARRIS V G,VITTORIA C,et al.A quantitative model for the nonlinear response of fluxgate magnetometers[J].Journal of applied physics,2006,99(08B3161):1-3.

[56] 吴德会,李雪松,黄一民,等.利用局部磁滞回线特性的无损检测新方法[J].仪器仪表学报,2015,36(10):2207-2214.

[57] PETRUCHA V,KASPAR P,RIPKA P,et al.Automated system for the calibration of magnetometers[J].Journal of applied physcis,2009,105(07E704):1-3.

[58] MERAYO J M G,BRAUER P,PRIMDAHL F,et al.Scalar calibration of vector magnetometers[J].Measurement science and technology,2000,11:120-132.

[59] PYLVANAINEN T.Automatic and adaptive calibration of 3D field sensors[J].Applied mathematical modelling,2007,32:575-587.

[60] ALONSO R,SHUSTER M D.Centering and observability in attitude independent magnetometer bias determination[J].The journal of the astronautical sciences,2003,51(2):133-141.

[61] 黄琳,荆武兴.卫星姿态确定与三轴磁强计校正[J].宇航学报,2008,29(3):854-859.

[62] CRASSIDIS J L,LAI K L.Real-time attitude-independent three-axis magnetometer calibration[J].Journal of guidance of control and dynamics,2005,28:115-120.

[63] 吴德会,黄松岭,赵伟.基于FLANN 的三轴磁强计误差校正研究[J].仪器仪表学报,2009,30(3):449-453.

[64] 张晓明,赵剡.基于椭圆约束的新型载体磁场标定及补偿技术[J].仪器仪表学报,2009,30(11):2438-2443.

[65] 龙达峰,刘俊,张晓明,等.基于椭球拟合的三轴陀螺仪快速标定方法[J].仪器仪表学报,2013,34(6):100-106.

[66] 朱建良,王兴全,吴盘龙,等.基于椭球曲面拟合的三维磁罗盘误差补偿算法[J].中国惯性技术学报,2012,20(5):562-566.

[67] 石岗,李希胜,李雪峰,等.航向测量系统中三轴磁传感器标定的等效两步法[J].仪器仪表学报,2017,38(2):402-407.

[68] 黄玉,郝燕玲.水下磁异常定位中两种矢量磁力仪配置方式的比较[J].中国惯性技术学报,2009,17(6):677-682.

[69] PANG H F,LUO S,ZHANG Q,et al.Calibration of a fluxgate magnetometer array and its application in magnetic object localization[J].Measurement science and technology,2013,24(7):075102.

[70] LASSAHN M P,TRENKLER G.Vectorial calibration of 3D magnetic field sensor arrays[J].IEEE transactions on instrumentation and measurement,1995,44(2):360-362.

[71] BONGARD M W,FONCK R J,LEWICKI B T,et al.A hall sensor array for inertia current profile constraint[J].Review of scientific instruments,2010,81(10E105):1-4.

[72] 吴永亮,王田苗,梁建宏.微小型无人机三轴磁强计现场误差校正方法[J].航空学报,2011,32(2):330-336.

[73] 庞鸿锋.捷联式地磁矢量测量系统误差分析及校正补偿技术[D].长沙：国防科学技术大学,2015.

[74] CLEM T,ALLEN G,BONO J,et al.Magnetic sensors for buried minehunting from small unmanned underwater vehicles[C]∥Proc of SPIE.2004:902-910.

[75] ALLEN G I,SULZBERGER G,BONO J T,et al.Initial evaluation of the new real-time tracking gradiometer designed for small unmanned underwater vehicles[C]∥Proceedings of OCEANS 2005 MTS/IEEE.2005:32-40.

[76] SULZBERGER G,BONO J,ALLEN G I,et al.Demonstration of the real-time tracking gradiometer for buried mine hunting while operating from a small unmanned underwater vehicle [C]∥Proceedings of Oceans 2006.2006:1-5.

[77] 于振涛,吕俊伟,毕波,等.四面体磁梯度张量系统的载体磁干扰补偿方法[J].物理学报,2014,63(11):139-144.

[78] 龙礼,张合,丁立波.三维磁传感器最大似然估计椭球拟合补偿算法[J].南京理工大学学报(自然科学版),2013,37(5):716-719.

[79] 李季.地磁测量中载体干扰磁场特性及补偿方法研究[D].长沙：国防科学技术大学,2013.

[80] 张光,张英堂,尹刚,等.一种磁张量探测系统载体的磁张量补偿方法[J].地球物理学报,2016,59(1):311-317.

[81] 杨云涛.导航载体干扰地磁测量误差补偿技术和地磁图建模研究[D].石家庄：军械工程学院,2009.

[82] 王维.地磁定向中的抗干扰技术研究[D].石家庄：军械工程学院,2009.