借助几何直观深化概念理解

郑晓婧

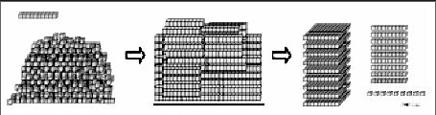
【摘要】在新课程的背景下，当教师教学某一部分数学知识的时候，除了关注知识本身，更重要的是要关注知识背后“大的思想”，也就是知识背后核心的数学思想方法和文化内涵.从“计数单位直观模型”到“计数器直观模型”再到“数学模型”的建构过程，由此引发学生对位值制的深刻理解.在教学中，将借助教材提供的直观模型——小方块，由零散到系统、逐层深入、细致地展示了计数单位的形成过程，让学生深刻体会到了计数过程中“单位”“位值”“满十进一”等重要思想.

【关键词】数学；模型

一、借助多种模型，让学生经历完整数学建模过程

数的认识隐含的数学思想就是十进位值制计数法，而对十进位值制计数法的理解，首先，就是对计数单位的理解.面对计数单位这样抽象、难以理解的概念，在教学中如何做到润物无声、浸润心田呢？我采用的教学策略是：以多样化的模型为支撑，帮助学生理解抽象的数概念，而有了丰富的数学模型后，学生所认识的数概念就有了参照物，就能更好地发展其数感.再借助多种模型，认识计数单位“千”“万”，感受位值制思想这一环节时，我预设如下教学.

1.课件出示一堆凌乱的正方体，学生估计数量.

2.数一数：无序堆放—有序摆放.

（1）把上述凌乱的正方体整理，有序摆放.

（2）学生在计数器上拨出999.

（3）提问：这三个“9”，表示的意思一样吗？

模型是帮助学生理解抽象的数概念的最好支撑，首先，借助计数单位直观模型——小正方体，由零散到系统、逐层深入、细致地展示了计数单位的形成过程，让学生深刻体会到了计数过程中“单位”“位值”等重要思想.在整理数出小正方体个数的过程中，学生真正经历了一次“数学建模”的过程，即从“计数单位直观模型”到“计数器直观模型”，再抽象为“数学模型”；进而通过“999”这一特殊数字，由此引发学生对位值制的思考和感悟：这3个“9”由于出现在不同的数位上，所代表的数值也就不同，所以用数位计数是一个简便、科学的好办法.这样不仅培养了学生的数感，也帮助学生对位值制有更深刻的理解.

这样，借助教材提供的直观模型——小方块，由直观具体到抽象概括，揭示了计数单位的形成过程，让学生深刻体会到了计数过程中“单位”“位值”“满十进一”等重要思想，经历了一次数学建模的完整过程.

二、打破教学常规，让学生经历“再创造”的思考过程

数与数学如影随形，无论对数学学科还是数学学习来说，数概念都是最为重要的基石.只要对自然数的产生与扩展过程稍微有些了解，就不能不敬畏人类创造位值制的智慧.马克思赞十进制计数法是“最妙的发明之一”.然而，由于现在人们对自然数太过熟悉了，并且在学习中自然而然地接受了十进制计数规则，已经很难体会到创造位值制是多么了不起的事，其数学思想与文化内涵被淹没在知识的海洋中.因为就这些数字本身来说，完全可以用其他的符号来代替.位值制更重要的价值内核是建立了一套简单而實用的规则，即把一个数字放在不同的位置上表示出不同的数值，也就是数位不同计数单位也不同.按照这个规则，仅用10个数字就可以表示出无穷无尽的自然数.在教学中，如果只是把“满十进一”作为结果来教学，而没有深层的思考，不去关注知识的发生过程，那么这样的教学只是知识的传授，还谈不上是智慧的发展.

三、挖掘文化内涵，让学生体会人类设计计数规则的智慧

在本堂课教学中，创设“古人计数”的情境，让学生用手指头来数羊，数到10后，手指头不够用了，由此了解十进制的起源，渗透数学文化；中国古代的算筹计数法和现代通行的十进位制计数法是完全一致的.通过中国算筹数码的简单介绍和让学生观察同样一根算筹，在不同数位所表示的数值不一样，初步感知位值制（个位、十位、百位），为后续学习打下基础.同时，联系《三字经》中“一而十，十而百，百而千，千而万”的句子，从另一角度表述了数学中“满十进一”的道理及计数单位之间的十进制关系.教师巧妙利用这一文化资源，既渗透数学文化，又较好地帮助学生理解并记忆计数单位之间的关系.

总之，为了把握数概念的核心“数感”——“位值制”.我通过创设古人计数情境，让学生了解十进制起源，初步感知位值制；让学生观察丰富图片，感受生活中的大数，体验学习大数的必要性；借助多种模型，让学生认识计数单位“千”“万”，感受位值制思想；通过多种方式，感受“千”“万”的大小，真正发展学生的数感等环节，让学生进一步理解计数单位之间十进制关系，感受位值制思想，经历数学建模过程，体会人类计数规则的伟大智慧，从科学预设到有效的生成的过程正是学生经历从知识到智慧的过程.