具有工作休假的离散时间Geo/Geo/1重试排队系统
2017-04-26彭懿
彭 懿
(长沙师范学院初等教育系,中国 长沙 410100)
具有工作休假的离散时间Geo/Geo/1重试排队系统
彭 懿
(长沙师范学院初等教育系,中国 长沙 410100)
研究了具有工作休假的离散时间Geo/Geo/1重试排队系统. 服务台具有工作休假模式,休假时间服从几何分布并且不能被打断. 分析了此排队系统的马氏链, 得到了系统稳态存在的充要条件. 利用系统演化的平衡方程组求出了重试组队长和服务台状态的联合平稳分布. 最后利用重试组队长的概率母函数, 进一步得到了一系列重要的排队性能指标.
离散时间重试排队系统;工作休假;拟生灭过程
近年来, 越来越多的文献探究了重试排队系统, 特别是连续时间重试排队系统. 重试排队系统是指顾客到达系统时, 若发现服务台空闲则立即接受服务; 若发现服务台忙但有空的等待位置, 则按某种排队规则在队列中等待服务; 若发现服务台忙且所有的等待位置均被占据, 则进入重试组不断重试直到成功接受服务. 重试排队系统广泛应用于电话交换系统, 通信网络以及计算机网络等领域. 电话订票系统和网上订票系统都可理解为重试排队系统, 包括无线网络的计算机和具有以太网类协议的局域网. 有关重试排队系统的主要研究方法和成果, 有Yang和Templeton[1], Falin[2]以及Falin和Templeton等[3]. 目前重试排队系统的研究主要集中于连续时间的情形. 然而, 在一些应用中, 离散时间重试排队系统比连续时间重试排队系统更加适合模拟计算机通讯系统和电信系统. 这是因为在许多通信系统中, 时间被划分为可作为一个时间单位的时隙. 例如, 在ATM网络中, 每个单元具有固定的大小和服务时间. 系统从一个状态转换到另一个状态只发生在时隙的开始或结束. 尽管离散时间重试排队系统十分重要, 关于这方面的研究工作却很少.
在过去三十年中, 很多学者致力于研究休假排队系统. 休假是指服务台终止在队列中服务, 服务台可能正在修复, 或者是被迫停止服务. 休假排队系统已广泛用于通信系统, 计算机网络, 生产管理, 业务管理的性能分析等许多现实生活应用中. 关于休假排队系统的文献参见Doshi[4], Takagi[5]以及Tian和Zhang[6]等. 在这些研究中, 通常假设服务器在休假期间停止服务. 最近, 越来越多的学者感兴趣于工作休假排队系统. 工作休假是指当服务台休假时并不完全停止服务, 只是服务速度比正常工作时的服务速度要慢. Servi和Finn[7]首先研究了M/M/1工作休假排队系统. Wu和Takagi[8]将这项工作扩展到多重工作休假的M/G/1排队系统. Baba[9]考虑了具有多重工作休假的GI/M/1队列. Li[10]分析了具有工作休假的GI / Geo / 1离散时间排队系统. Tian 等[11]研究了具有多重工作休假的Geo/Geo/1离散时间排队系统. Li[12]分析了指数工作休假的M/G/1排队系统. Chae[13]探究了单重工作休假的GI/M/1队列和GI/Geo/1排队系统. Goswami和Selvaraju[14]研究了多重工作休假的MAP/PH/1离散时间排队系统. Do[15]考虑了工作休假的M/M/1重试排队系统. Li等[16]研究了具有工作休假且休假可被打断的离散时间Geo/Geo/1重试排队系统. 然而, 他们的模型并不能包含具有工作休假且休假不能被打断的离散时间重试排队系统. 其次, 当其模型中的重试率趋于无穷时, 其稳定性条件与离散时间Geo/Geo/1队列的稳定性条件不一致. 所以我们试图重新探究具有工作休假的离散时间重试排队系统.
本文重新探究具有多重工作休假的离散时间Geo/Geo/1重试排队系统, 得到一系列非常重要的排队性能指标. 本文的研究主要应用于无线网络中的媒体访问控制功能的性能分析[17].
1 模型描述
考虑一个单服务台的离散时间重试排队系统, 系统时间轴被分割成等长的时隙. 离散时间重试排队系统中的所有事件都只能发生在时隙的分点处. 时间轴被分割为0,1,…,m,…. 假设顾客的离开只能位于时隙(m-,m)处, 顾客的到达和重试点依次只能在时隙首端(m,m+)处. 休假的开始和结束也只能发生在时隙m+处. 这里m-表示时刻前一瞬间,m+表示时刻m后一瞬间. 即本文考虑的是早到系统(EAS)情形. EAS的相关概念参见Hunter[18].
顾客的到达服从参数为p的Bernoulli过程. 服务台前无等待位置, 因此, 若顾客到达系统时发现服务台空闲则立即开始服务, 否则, 按先到先服务规则进入重试组, 即只有队首的顾客允许重试. 重试时间服从参数为δ的几何分布. 当某次服务结束时, 重试组中若无顾客,服务台开始一个工作休假, 休假时间服从参数为θ的几何分布, 即在任意一个时隙末端, 系统以概率θ结束工作休假. 在服务台正常工作期间和工作休假期间服务时间分别服从参数为μb和μv(μv<μb)的几何分布. 一个工作休假结束时, 若系统中有顾客等待, 则结束工作休假进入正常工作状态, 即服务率由μv转为μb; 否则继续开始一个新的工作休假.

2 模型求解及性能指标分析
在时刻m+, 令Nm表示重试组中的顾客数, 并记服务台的状态变量为Jm.Jm=0表示服务台处于工作休假和闲期;Jm=1表示服务台处于工作休假和忙期;Jm=2表示服务台处于闲期且不在工作休假;Jm=3表示服务台处于忙期且不在工作休假. 易知, 马氏链Ψ={(Nm,Jm),m≥1}是一个离散时间拟生灭过程, 其状态空间为
Ω={(i,j):i≥0,j=0,1,3;(i,2):i≥1}.
以下的主要工作是求马尔可夫链Ψ的平稳分布
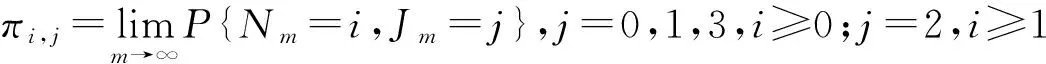
将状态空间按照字典顺序排序, 得到QBD过程的转移概率矩阵P为

其中
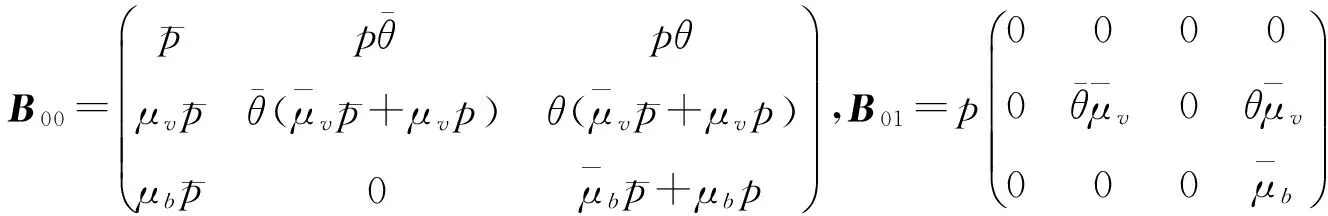
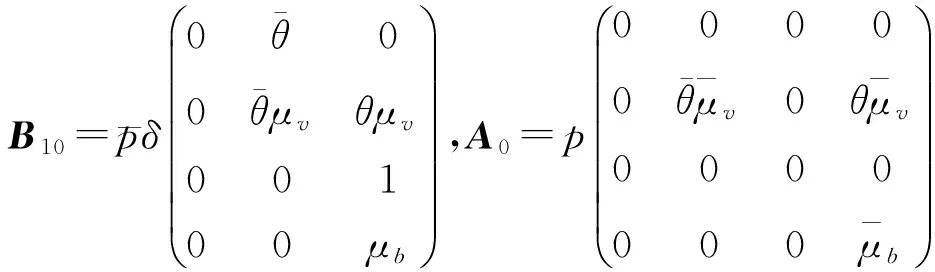
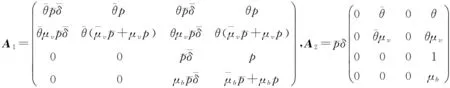
此排队系统的稳态存在条件由以下定理给出

证 显然此QBD过程不可约. 矩阵A=A0+A1+A2为
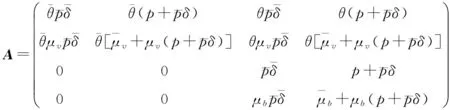
则矩阵A是不可约的随机矩阵. 根据文献[19]中定理7.3.1此QBD过程Ψ是正常返的当且仅当

(1)
其中ν=νC1,νe=1,e表示所有分量为1的一列向量. 这里

经过一系列复杂的代数运算, 得到
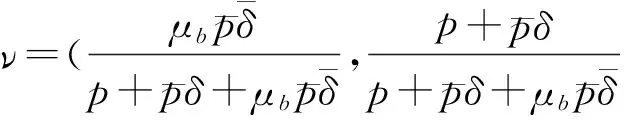
(2)

3 平稳分布
这一节,通过求解系统稳态分布的Kolmogorov方程推导出重试组队长的概率母函数和一系列重要的排队性能指标. 利用快速Fourier变换方法,可以计算重试组队长稳态分布的各阶矩.
我们记转移概率矩阵P对应的平稳向量为Π=(Π0,Π1,…), 其中Π0=(π0,0,π0,1,π0,3),Πk(πk,0πk,1,πk,2,πk,3),k≥1. 系统演化的平衡方程如下
Π0B00+Π1B10=Π0,
Π0B01+Π1A1+Π2A2=Π1,
Πk-1A0+ΠkA1+Πk+1A2=Πk,k≥2.
因此, 描述系统平稳分布的Kolmogorov方程为:
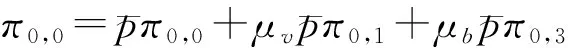
(3)
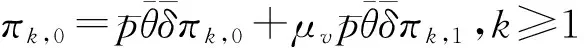
(4)

(5)

(6)
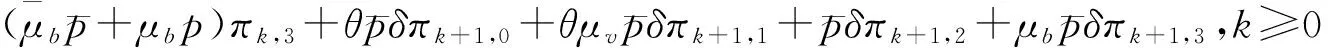
(7)
其中δi,j为Kronecker记号, 其归一化条件为
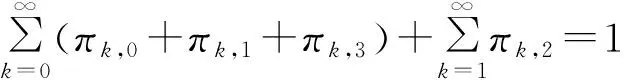
(8)
为求解方程(3)~(8), 引入如下概率母函数:

将方程(4)~(7)左右两边同乘zk,然后对k求和,得到
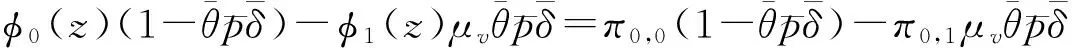
(9)

(10)
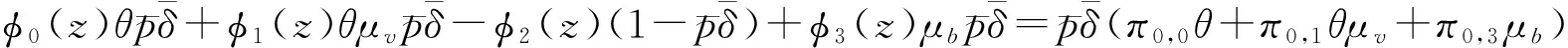
(11)
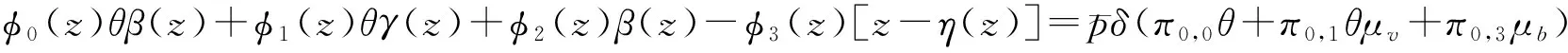
(12)
其中

由(9)和(10), 得到母函数φ1(z)和φ0(z)为
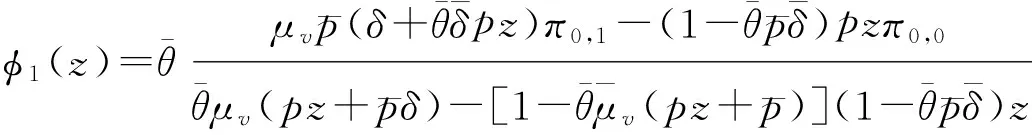
(13)

(14)
由(11)和(12), 得到母函数φ3(z)和φ2(z)为
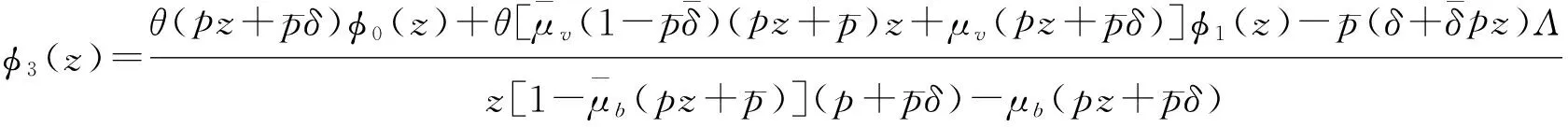
(15)
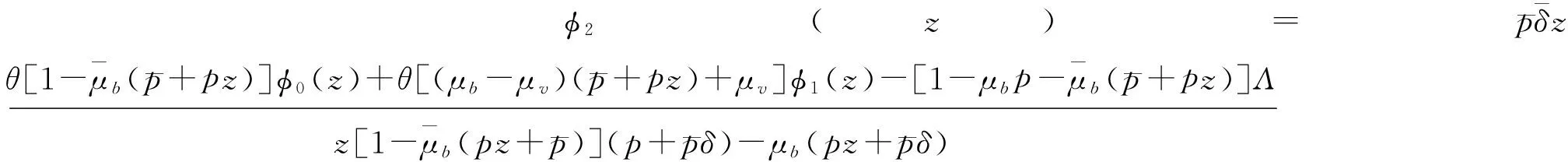
(16)
其中
Λ=π0,0θ+π0,1θμv+π0,3μb.
为了推导未知数π0,0,π0,1和π0,3, 需要下述引理.

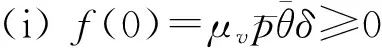
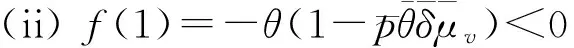
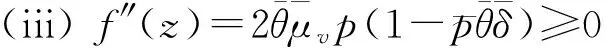
所以函数f(z)区间[0,1]恰好有一个根. 证毕.
根据引理1,φ1(z)的分母在点z0处等于零. 而φ1(z)在|z|≤1是解析的, 所以有
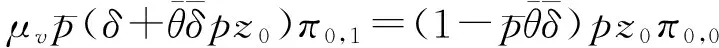
或
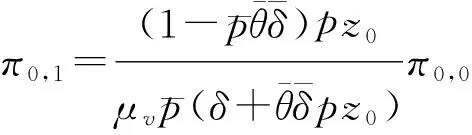
(17)
将(17)代入(3), 得到
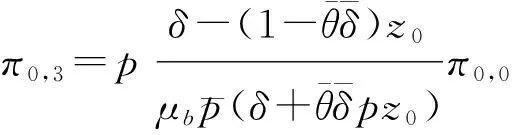
(18)
将(17)和(18)代入(13)~(16)知道如φ0(z),φ1(z),φ2(z)和φ3(z)只依赖于未知数π0,0. 最后,π0,0可由归一化条件(8)得到.
将以上结论总结为下述定理.
定理1 QBD过程Ψ的平稳分布具有以下母函数
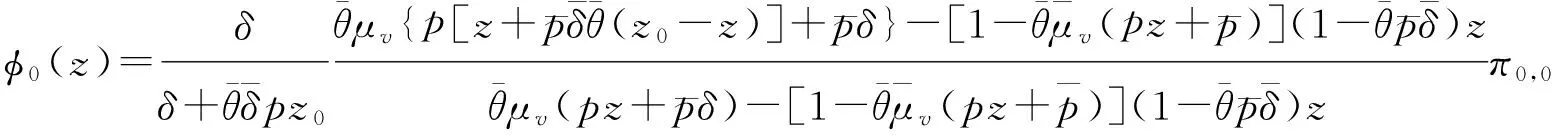
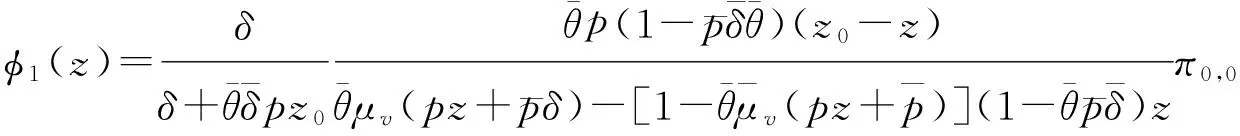
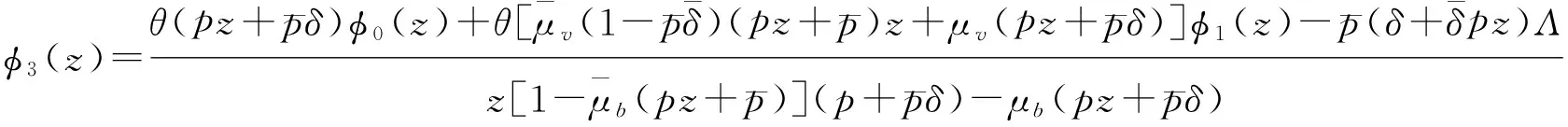
其中

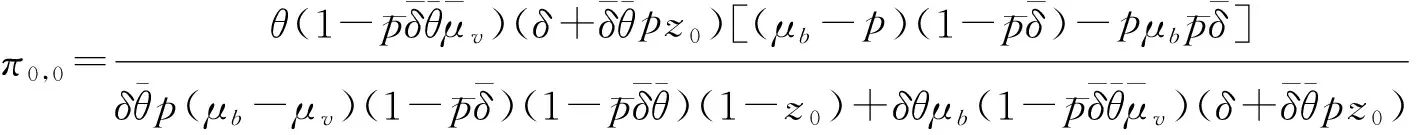

下述推论给出此排队系统稳态时的一些性能指标.
推论1:
(1)系统空的概率为

(2)服务台空闲且处于工作休假状态的概率为
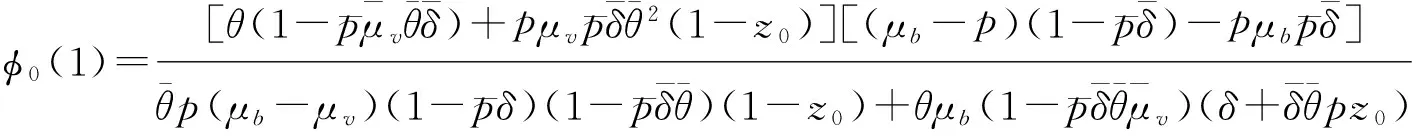
(3)服务台忙且处于工作休假状态的概率为
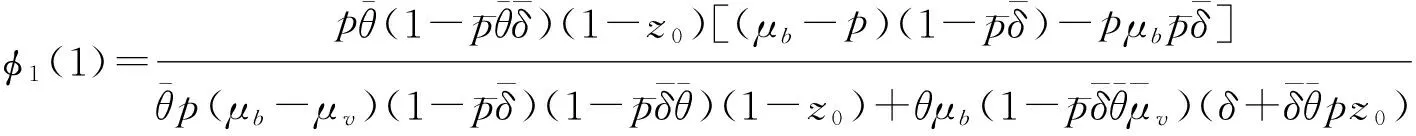
(4)服务台空闲且处于正常工作状态的概率为
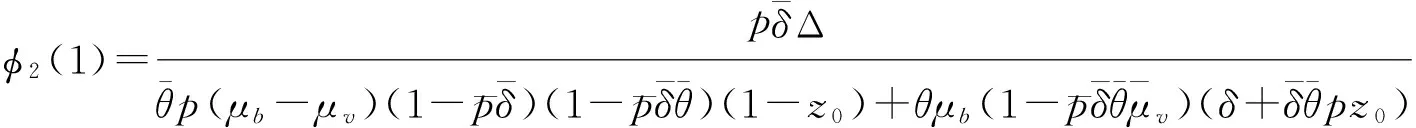
其中
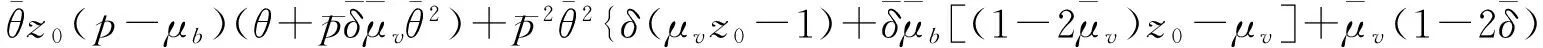
(5)服务台忙且处于正常工作状态的概率为
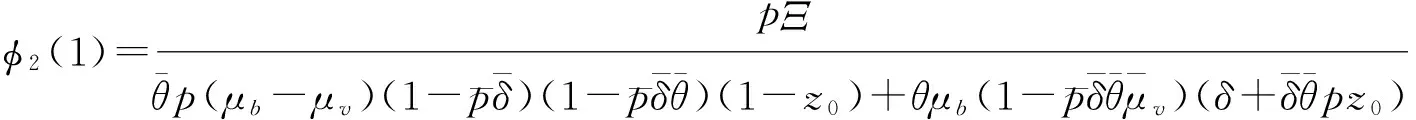
其中
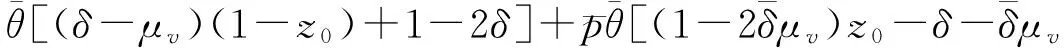
(6)服务台忙的概率为
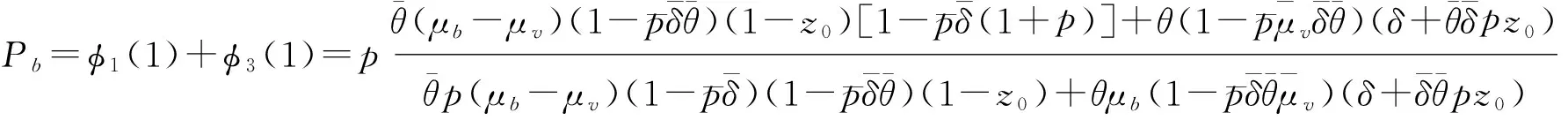
(7)服务台空闲的概率为
PI=φ0(1)+φ2(1)=1-Pb=

(8)重试组平均队长为
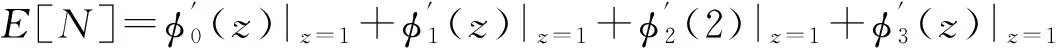
[1] YANG T, TEMPLETON J. A survey on retrial queues[J]. Queueing Syst, 1987,2(3):201-233.
[2] FALIN G. A survey of retrial queues[J]. Queueing Syst, 1990,7(2):127-167.
[3] FALIN G, TEMPLETON J. Retrial queues[M]. London: Chapman & Hall, 1997.
[4] DOSHI B. Queueing systems with vacations: a survey[J]. Queueing Syst, 1986,1(1):29-66.
[5] TAKAGI H. Queueing Analysis: a foundation of performance evaluation, Vacation and Priority Systems, Part I.[M]. Amsterdam: North-Holland, 1991.
[6] TIAN N, ZHANG Z. Vacation queueing models—theory and applications[M]. New York: Springer Science, 2006.
[7] SERVI L, FINN S. M/M/1 queue with working vacations (M/M/1/WV) [J]. Perf Eval, 2002,50(1):41-52.
[8] WU D, TAKAGI H. M/G/1 queue with multiple working vacations[J]. Perf Eval, 2006,63(7):654-681.
[9] BABA Y. Analysis of a GI/M/1 queue with multiple working vacations[J]. Oper Res Lett, 2005,33(2):201-209.
[10] LI J, TIAN N, LIU W. Discrete-time GI/Geom/1 queue with multiple working vacations[J]. Queueing Syst, 2007,56(1):53-63.
[11] TIAN N, MA Z, LIU M. The discrete time Geom/Geom/1 queue with multiple working vacations[J]. Appl Math Model, 2007,32(12):2941-2953.
[12] LI J, TIAN N, ZHANG Z,etal. Analysis of the M/G/1 queue with exponentially working vacations-a matrix analytic approach[J]. Queueing Syst, 2009,61(1):139-166.
[13] CHAE K, LIM D, YANG W. The GI/M/1 queue and the GI/Geo/1 queue both with single working vacation[J]. Perf Eval, 2009,66(2):356-367.
[14] GOSWAMI C, SELVARAJU N. The discrete-time MAP/PH/1 queue with multiple working vacations[J]. Appl Math Model, 2010,34(4):931-946.
[15] DO T. M/M/1 retrial queue with working vacations[J]. Acta Inform, 2010,47(1):67-75.
[16] LI T, WANG Z, LIU Z. Geo/Geo/1 retrial queue with working vacations and vacation interruption[J]. J Appl Math Comput, 2012,39(1):131-143.
[17] ARORA A, JIN F, SAHIN G,etal. Throughput analysis in wireless networks with multiple users and multiple channels[J]. Acta Inform, 2006,43(1):147-164.
[18] HUNTER J. Mathematical techniques of applied probability, vol. 2, discrete-time models: techniques and applications[M]. New York: Academic Press, 1983.
[19] LATOUCHE G, RAMASWAMI V. Introduction to matrix analytic methods in stochastic modeling[M]. Alexandria: ASA-SIAM Series on Applied Probability, 1999.
[20] ATENCIA I, MORENO P. A discrete-time Geo/G/1 retrial queue with general retrial times[J]. Queueing Syst, 2004,48(1):5-21.
(编辑 CXM)
重要启事
“优先数字出版”是以纸质版期刊录用稿件为出版内容,先于纸质期刊出版日期出版的数字期刊出版方式.我刊已于2012年起与中国学术期刊(光盘版)电子杂志社签订了优先数字出版协议.凡被我刊录用的稿件一经优先数字出版,读者即可在中国知网(CNKI)全文数据库进行检索和下载.凡向本刊投稿的作者,如无特别申明,均被视为作者授权本刊编辑部在纸质期刊出版前,可以在中国学术期刊(光盘版)电子杂志社主办的“中国知网”(www.cnki.net)上优先数字出版;也被视为作者同意并授权我刊与其他电子杂志社签订的协议,并许可其在全球范围内使用该文的信息网络传播权、数字化复制权、数字化汇编权、发行权及翻译权,并不再额外支付稿酬.
本刊编辑部
The Discrete-Time Geo/Geo/1 Retrial Queue with Working Vacations
PENGYi*
(Junior Education Department, Changsha Normal University, Changsha 410100, China)
The classical Geo/Geo/1 retrial queue with working vacations was studied, where working vacations are geometric distributed and cannot be interrupted. The Markov chain underlying the considered queueing system was analyzed and its stability condition was derived. Using the balance equations, the steady-state joint distribution of the number of customers in the obit and the states of the server was obtained. Furthermore, the generating functions of the number of customers in the orbit was found and some performance measures of the system in the steady-state was presented.
discrete-time retrial queues; working vacations; QBD
10.7612/j.issn.1000-2537.2017.02.015
2017-01-07
国家自然科学基金数学天元基金资助项目(11626045);湖南省自然科学基金资助项目(2016JJ6001);湖南省教育厅资助科研项目(15C0100)
O122
A
1000-2537(2017)02-0089-06
*通讯作者,E-mail:pengyiqueue@163.com
