试论初中数学辅助线的应用方法

徐威

摘 要：辅助线一直都是解决几何问题中不可或缺的，通过辅助线的有效添加，不仅可以使得相应问题得到更好、更便捷的解答，也能够给学生留下更深刻的印象。同时，在利用题目提供的条件无法有效解决问题时，通过添加相应辅助线，可以获得新的条件，也能够为学生提供新的问题解决思路，促进其学习、解题效率的不断提升。

关键词：初中数学；辅助线；应用方法

一直以来，不论在哪一阶段，辅助线在数学解题中的地位都是至关重要的，在加上数学题目的变化往往都是灵活无穷的，因此，辅助线的添加方式也是灵活多样的。不论那一道几何题，图形与条件都是必不可少的两部分，而通过结合其图形、条件具有的特殊性巧妙的添加辅助线，不仅可以使得原本复杂、难懂的题目迎刃而解，也能够不断拓展学生解题思维，为其今后的学习、解题提供有力参考，不断提升学生解题效率。

一、辅助线在三角形中的科学运用

对于三角形中辅助线的添加来讲，主要是结合问题特点与需求来进行辅助线的科学运用。例如，在无法利用现有条件将三角形三边关系直接证明出来时，可以将其中一边延长，也可以通过将其两点连接来构成三角形，以此来得出其线段在一个或是多个三角形中的结论，然后再利用三角形三边的不等关系来进行证明；又如：在无法利用现有条件将三角形外角大于任何不与其相邻的内角这一定义直接证明出来时，就可以引导学生将某一边延长，或者是通过连接其中两点构成三角形，以此来让其小角位于其图形的内角，之后再证明出其大角处于其三角形的外角位置，在此基础上再运用相应外角定理来最终解答。此外，若题目中给出了平分线时，通常都是在其角的两边取相同的线段来构成全等三角形等。

上述只是总结了三角形辅助线比较常见的添加方式，但是对于数学辅助线的应用来讲，通常都是法无定法的，因此，要想将辅助线的积极作用充分发挥出来，并在解题中实现科学灵活运用，往往还是需要在实践解题练习中不断归纳与总结，不仅可以单独添加，也可以结合实际情况，进行恰当的组合运用，也只有这样在解答相应题目过程中才能够真正做到有的放矢，才能够引导学生真正掌握其运用规律与技巧，因此，出了总结、归纳外，其数学教师还应结合学生实际认知需求，积极为学生设计针对性较强的练习活动。

二、辅助线在圆形中的有效运用

对于圆形来讲，其添加辅助线的方法主要可以从以下几方面着手：

1.可以结合垂径平分的定理，过圆心做弦的垂线，在此基础上进行问题的解答。同时，也可以结合同圆、等圆中的圆周角、圆心角，以及弦、弧的互相转换关系，与圆上相关点进行连接来妥善解决其题目，为学生分析、解答相应题目提供全新思路。

2.若题目中给出了直徑的相关已知条件，通常情况下，都要结合“直径所对的圆周角是直角”这一定理来进行相关辅助线的添加，这样不仅可以保障准确性，也能够进一步拓展学生解题思路，促进其解题效率的不断提升。

3.若题目重给出了切线的相关已知条件时，一般都是进行过切点连接其半径或直径，充分考虑切线与其垂直的特点来进行问题的解析。或者是作过切点的弦，做好弦切角与圆心、圆周角之间关系的妥善处理与沟通，在此基础上更便捷的解答相应题目，这样不仅可以帮助学生巩固所学知识，也能够让其在此过程中积累到更多解题技巧与经验，激活其数学思维。

4.若题目中给出了两圆相切的已知条件，学生在解答时，教师应指导学会过切点作两圆的公切线，以此来更好的实现弦切角、圆周角间关系的沟通，拓展解题思路。也可以结合现有条件，作两圆的连心线，灵活利用其切点，在连心线上实现圆心距、两圆半径之间关系的有效沟通，通过其辅助线的巧妙添加，获得更便捷的解题方法。

5.在两圆处于相交状态时，对于这样的题目，教师可以指导学生作两圆的公共弦，并充分利用公共弦这一桥梁，更好的实现两圆圆周角、其他角之间关系的有效沟通，以此来为题目的证明提供更简便的思路，也进一步锻炼、提升学生实践探究解题能力。总之，圆形辅助线的添加方式有很多，为了使辅助线的积极作用能够在证明题目中充分发挥出来，教师应引导学生对题目现有条件、现有知识结构做出综合考虑，从而选择更适合、准确的辅助线添加方式，帮助学生积累更丰富的解题技巧与经验。

三、辅助线在平行四边形中的恰当运用

平行四边形主要包括正方形、菱形，以及矩形，这些图形的两组对边、对角等具有的性质都有一定的相似之处，所以，辅助线在这些图形中的添加方法一般都具有较大的相似性，往往都是为了实现线段的垂直与平行，在此基础上构成相应的全等、相似三角形。通常情况下，都是平移、连接图形对角线，或者是结合实际情况连接其中一边的中点与顶点等方式，从而将平行四边形巧妙转化成相应的矩形、三角形等图形，这样再分析解决其该题目则更加便捷。

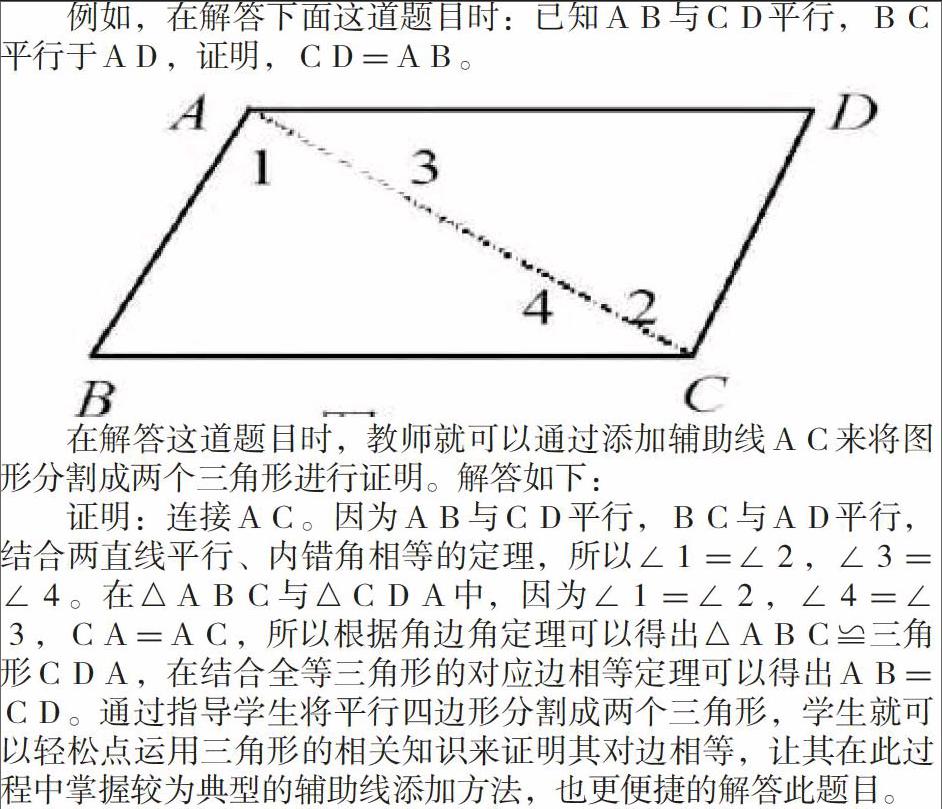
例如，在解答下面这道题目时：已知AB与CD平行，BC平行于AD，证明，CD=AB。

在解答这道题目时，教师就可以通过添加辅助线AC来将图形分割成两个三角形进行证明。解答如下：

证明：连接AC。因为AB与CD平行，BC与AD平行，结合两直线平行、内错角相等的定理，所以∠1=∠2，∠3=∠4。在△ABC与△CDA中，因为∠1=∠2，∠4=∠3，CA=AC，所以根据角边角定理可以得出△ABC≌三角形CDA，在结合全等三角形的对应边相等定理可以得出AB=CD。通过指导学生将平行四边形分割成两个三角形，学生就可以轻松点运用三角形的相关知识来证明其对边相等，让其在此过程中掌握较为典型的辅助线添加方法，也更便捷的解答此题目。

四、结语

总之，初中数学教师在带领学生学习、解答几何问题过程中应充分认识到，积极应用辅助线，对拓展学生解题思维，提升授课效率等方面的重要性。在教学实践中，其教师应结合实际需求与条件，带领学生不断总结几何题中添加辅助线的规律，指导其做出一个较为系统的总结。在此基础上，不仅可以进一步拓展学生解题思维，也能够让其在总结、实践应用中积累更多解题技巧与方法。

参考文献：

[1] 李蓉.例谈全等三角形问题中常见的辅助线的作法[J].都市家教（下半月），2016，（2）：118-119.

[2] 周美丽.初中数学解题中辅助圆的应用探析[J].新课程·中学，2014，（8）：158-158，159.

[3] 郑银凤.初中数学课外辅助读物的开发与运用[D].浙江师范大学，2013.