激发问题意识助推问题解决
2017-04-26徐昌陆黄琴
徐昌+陆黄琴
现代学习特别强调问题在学习活动中的重要性。一方面强调通过问题来学习,把问题看作是学习的动力、起点和贯穿学习过程中的主线;另一方面通过学习来生成问题,把学习过程看成是发现问题、提出问题、分析问题和解决问题的过程。笔者将以《圆锥的侧面展开图》教学为例,谈谈在现代课堂中如何激发学生问题意识,助推问题解决。
一、联系生活实际,激发问题意识
单纯的数学知识或数学问题往往枯燥无味,激不起学生的学习兴趣,教学中可以把需要学习的数学知识或数学问题与现实生活联系起来,渗透问题意识,激发学生思维。
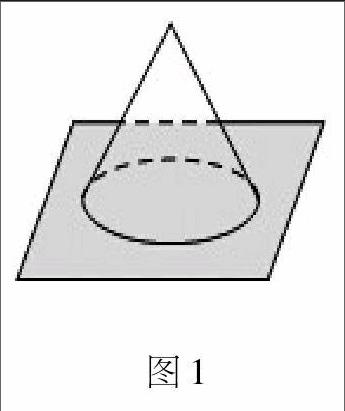
执教人教版《数学》九年级上册“圆锥的侧面展开图”环节,笔者首先出示教学情境:某农户在晒场上晒玉米,傍晚时分农户主人把玉米堆成如图1所示的形状,方便第二天继续晾晒。请学生根据情境提出一些问题。
学生以小组为单位讨论,提出了不少的问题:
1.这个玉米堆的形状是什么?
2.这堆玉米的体积是多少?
3.这堆玉米的重量是多少?
4.如何求这堆玉米的体积和重量?
5.如何测量玉米堆的底面积和高?
……
正当笔者准备进入下一个教学环节时,又有一位学生发言:“为预防下雨,如果农户主人准备用雨布把这堆玉米遮起来,至少需要多大面积的雨布?”
该学生能提出这样的问题,出乎笔者的意料,笔者不禁问道:“你是怎么想到这个问题的?”该生回答:“我的家住在农村,父母经常在院子里晒粮,为预防下雨,常常要把粮堆用雨布遮起来。”
笔者指出,这个问题涉及到圆锥的侧面积,它正是接下来我们要研究的问题。一石激起千层浪,学生又七嘴八舌地议论:“圆锥的侧面是什么形状?”“如何求圆锥的侧面积?”
学生之所以能提出这样的问题,与其生活经验有关。问题是生长新思想、新方法、新知识的种子,问题意识会激发学生强烈的学习愿望。
二、渗透思想方法,助推问题解决
学习数学知识或者解决数学问题,与学生已有的知识和经验有关。学生对圆柱比较熟悉,在学习圆锥的相关知识时,可以与圆柱作类比,有利于学生发现问题、掌握探究问题的方法。
笔者先请学生回顾圆柱的侧面展开图,并进一步提问:如何把圆柱的侧面展开?圆柱的侧面展开图是什么图形?圆柱的侧面展开圖与圆柱的各元素之间有什么关系?如何计算圆柱的侧面积和全面积?再让学生动手制作圆锥,并在每个小组挑选一个制作规范的圆锥,以小组为单位展开讨论。类比圆柱,学生提出如下问题,以问题为载体展开探究。
1.如何把圆锥的侧面展开?
2.圆锥的侧面展开图是什么图形?
3.圆锥的侧面展开图与圆锥的各元素之间有什么关系?
4.如何计算圆锥的侧面积和全面积?
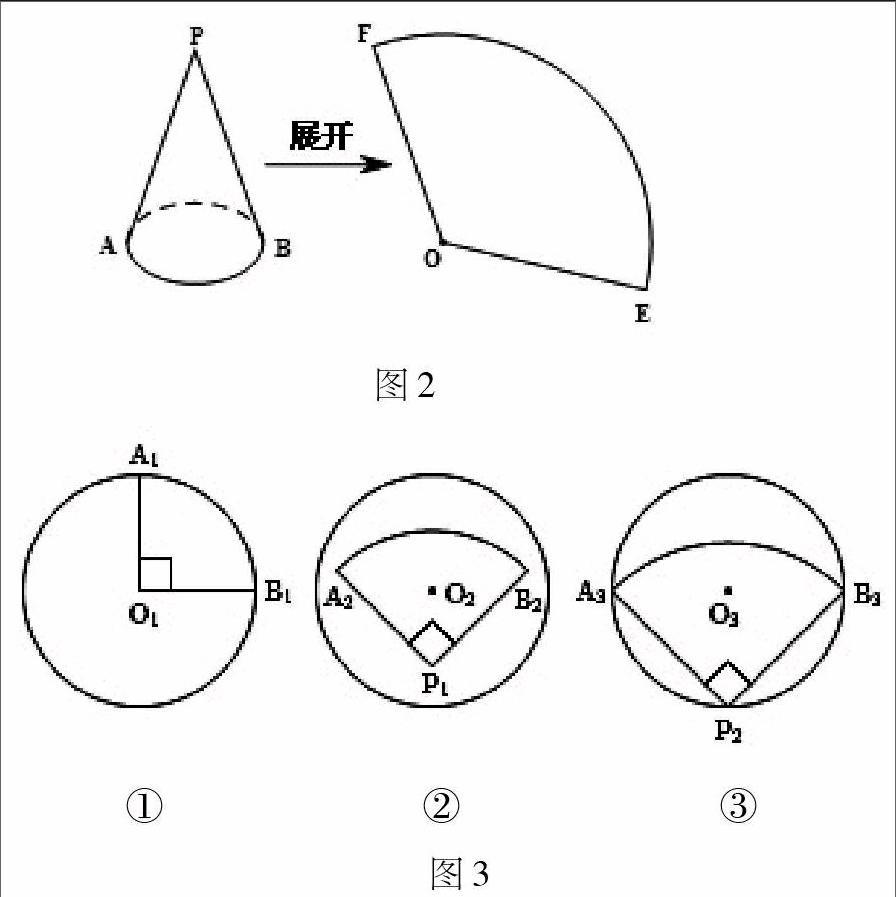
如图2,沿一条母线将圆锥侧面剪开并展平,观察发现,圆锥的侧面展开图是一个扇形。侧面展开图一出来,就有学生质疑:“为什么圆锥的侧面展开图是扇形?用什么方法来证明?”有学生说:“可以在曲线EF上任意找一点P,如果OP=OE,那么它就是扇形。”还有学生说:“可以用圆规画一画,以点O为圆心,OE为半径画弧,如果所画的弧与曲线EF重合,那么它就是扇形。”
好奇心驱使学生动起手来,有的学生用刻度尺量OP、OE的长度,有的学生用圆规画弧。事实证明圆锥的侧面展开图确实是一个扇形,接下来的问题学生根据展开图就很容易解决:展开图(扇形)的半径是圆锥的母线,弧形的弧长是圆锥底面圆的周长,圆锥的侧面积是侧面展开图扇形的面积,圆锥的全面积是侧面积与底面积的和。
类比的过程是同中辩异,异中求同的过程,也是知识系统化、结构化的过程。在类比中,学生可以触类旁通,找到解决问题的方法。
三、学会联想思考,开发问题潜能
数学学习是一个不断提出问题和解决问题的过程,能不能提出深层次、有价值的数学问题,贵在思考,联想是一种能开发问题潜能的思考方式。
圆锥的侧面展开图是个扇形,而扇形是圆的一部分,因此,扇形和圆之间存在着一定的关系。解决与圆锥有关的问题,往往离不开扇形和圆。
联想到“圆锥的侧面展开图是个扇形”和“扇形与圆之间的关系”等。你能提出一些什么样的问题?
问题1:由于“圆锥的侧面展开图是个扇形”,解决与圆锥有关的问题,要把圆锥与什么联系起来?
问题2:圆锥是立体图形,把圆锥的侧面展开得到一个平面图形(扇形)。反过来,用什么样的平面图形可以围成一个圆锥?
问题3:我们知道用扇形可以围成一个圆锥,而扇形与圆之间存在着一定关系。如何在半径为10cm的圆中剪下一个圆心角为90°的扇形围成一个侧面积最大的圆锥?
解决与圆锥有关的问题时,要把圆锥与扇形联系起来,画出圆锥和侧面展开图(扇形),可以直观地看出圆锥与扇形之间的关系,有利于问题的解决。
让学生画一画,剪一剪,通过制作圆锥,培养学生的动手、动脑能力,加深对圆锥与侧面展开图之间的关系的理解。
如图3,有的学生说按图①所示的方法剪,还有的学生说按图②所示的方法剪。这样问题又来了,用上述剪法围成圆锥的侧面积都不是最大的,那么如何剪才能围成侧面积最大的圆锥?
学生通过小组合作,集体讨论,互相比较,发现按图③所示的方法剪,即扇形所在圆的圆心P2和弧A3B3的两个端点A3、B3都在⊙03上,且∠A3P2B3=90°时,才能围成侧面积最大的圆锥。在此基础上,进一步求得圆锥底面圆的半径和圆锥的高。
联想是拓展思维的好方法,从问题发现到问题解决,让学生充分参与,展开联想,不仅渗透了数学思想,而且拓展了学生的思维空间,提升了学生发现问题和解决问题的能力。
(作者单位:徐昌陆,房县第一中学;黄琴,房县实验中学)
