期权组合保证金的最优化探讨

（申万宏源证券有限公司，上海 200031）

期权组合保证金的最优化探讨

顾宗源

（申万宏源证券有限公司，上海 200031）

本文系统地讨论了上海交易所推出的期权组合保证金方案对于50ETF期权持仓保证金的影响，并提出了数值最优化方法。研究结果表明，利用本文提出的方法可使得保证金占用减少80%以上，有效提高资金使用效率。

50ETF期权；保证金；最优化；高性能计算；做市

一、引言

经中国证监会批准，上海证券交易所决定于2015年2月9日上市交易上证50ETF期权合约品种[1]。上证50交易型开放式指数证券投资基金的证券简称为“50ETF”，证券代码为“510050”，基金管理人为华夏基金管理有限公司。2015年4月3日，上交所下发《关于就组合策略保证金交易与结算方案征求意见的通知》）（以下简称《通知》）[2]，《上海证券交易所股票期权组合策略保证金交易方案》（以下简称《方案》）[3]。

二、《方案》介绍

1、期权介绍

期权又称为选择权，是在期货的基础上产生的一种衍生性金融工具，指在未来一定时期可以买卖的权利，是买方向卖方支付一定数量的金额（指权利金）后拥有的在未来一段时间内（指美式期权）或未来某一特定日期（指欧式期权）以事先规定好的价格（指履约价格）向卖方购买或出售一定数量的特定标的物的权利，但不负有必须买进或卖出的义务。从其本质上讲，期权是在金融领域中将权利进行定价，使得权利的受让人在规定时间内对于是否进行交易，行使其权利，而义务方必须履行。在期权交易时，购买期权的一方称作买方，而出售期权的一方则叫做卖方；买方即是权利的受让人，而卖方则是必须履行买方行使权利的义务人。按照现有期权交易规则，对于期权的卖出方需要缴纳一定费用的开仓保证金。

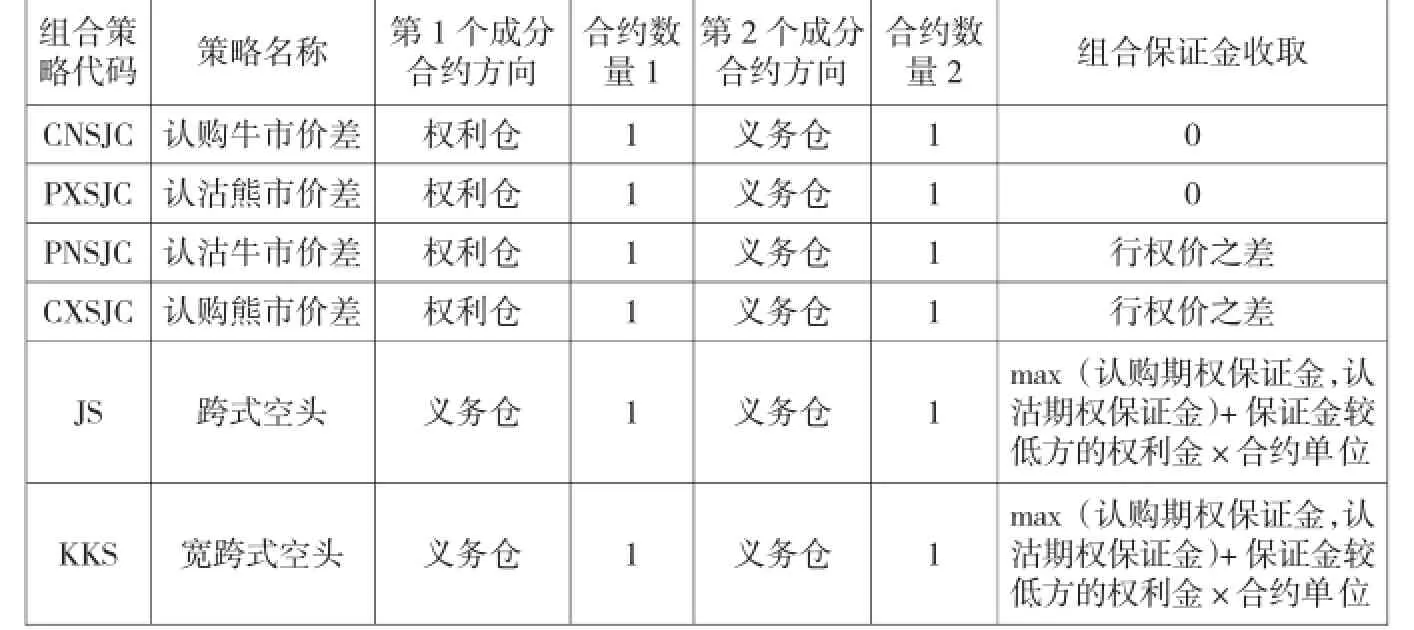
表1 组合保证金规则

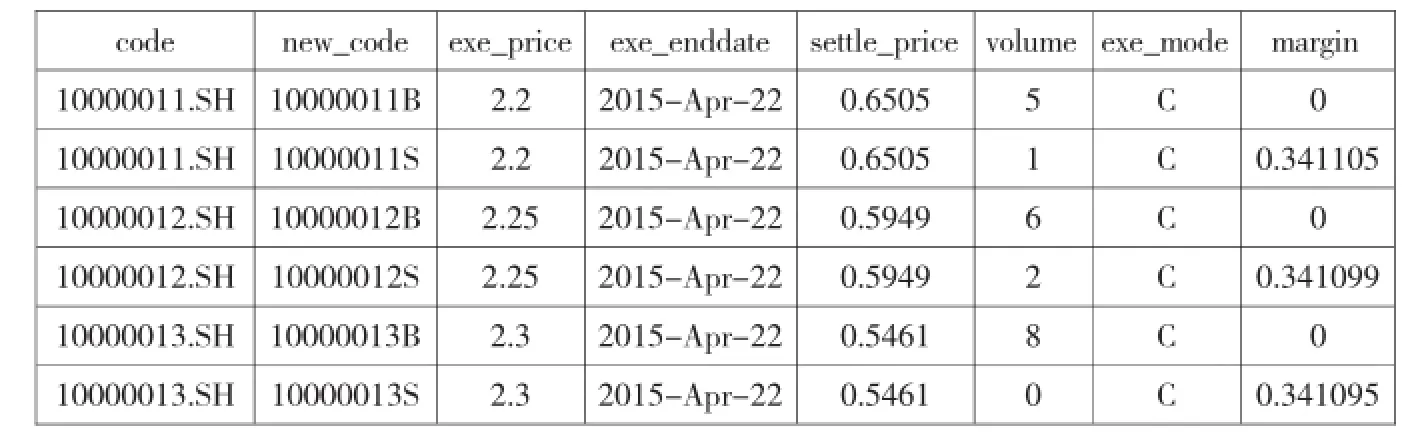
表2 编号示例

合约标的为交易型开放式指数基金（以下简称“交易所交易基金”）的，每张合约的开仓保证金的计算公式为：

（a）认购期权义务仓开仓保证金＝[合约前结算价+ Max（12%×标的前收盘价-认购期权虚值，7%×标的前收盘价）]×合约单位

（b）认沽期权义务仓开仓保证金＝Min{合约前结算价+Max[12%×标的前收盘价-认沽期权虚值，7%×行权价]，行权价}×合约单位

前款中的认购期权虚值＝Max（行权价-标的前收盘价，0）

认沽期权虚值＝Max（标的前收盘价-行权价，0）

对于期权经营机构，尤其作为期权做市商，每日的卖出期权持仓非常巨大，这些仓位占用的大量保证金在很大程度上造成了资金的闲置。

2、组合保证金实施方案

按照《方案》的设计，组合策略保证金是指通过构建组合策略达到保证金冲销或减免的目的，投资者可根据自身持仓，通过期权经营机构向上海证券交易所交易系统申请构建组合策略或解除组合策略。

构建组合策略指由投资者申报构建组合策略指令，将多个成分合约的持仓构建成一个组合策略持仓。经交易所交易系统校验确认后，即时返还多余保证金。解除组合策略指由投资者申报解除组合策略指令，将已建组合策略拆分成多个成分合约的持仓，经交易所交易系统检查确认，需检查拆分后各单个成分合约保证金是否足额，并确认补足保证金后，才能拆分成功。

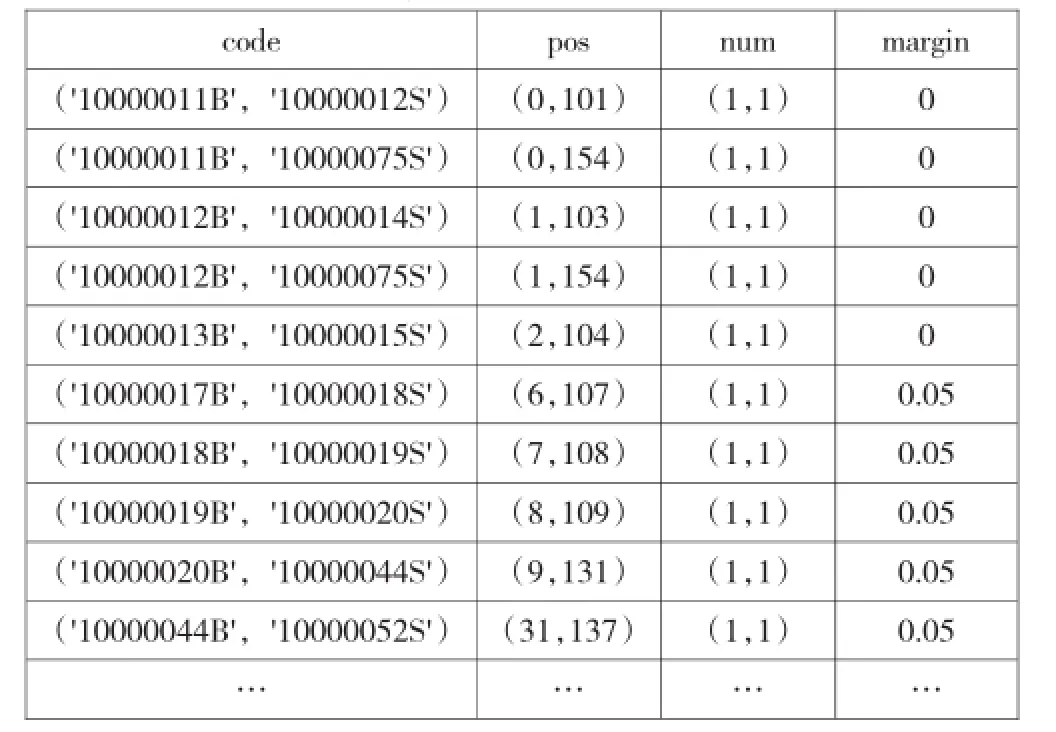
表3 组合示例

3、组合策略清单

前期拟提供的策略及相应保证金收取规则如表1所示。

三、数学最优化问题

与传统股票投资只有买入和空仓两种状态不同，对于期权交易可以分为认购买入开仓、认购卖出开仓、认沽买入开仓、认沽卖出开仓（这里暂时不讨论相应的备兑开仓情况）。在这里我们针对每张期权合约，分别就权利仓（买入）和义务仓（卖出）给他们重新编号（见表2）。

以 2015年4月22日到期的 10000011、10000012、10000013认购合约为例，它们行权价分别为2.2、2.25、2.3，将它们以不同买卖方向重新编号后（10000011B、10000012B、10000013B、10000011S、10000012S、10000013S）可以看到，在保证金一栏（margin）中，只有卖出方向（S编号）会收取相应的保证金。

对所有的期权按照《方案》的可行组合进行组合（见表3）。

以2015年4月5日市场行情为例，原期权合约为100个，按《方案》构建的可行组合为1555个，故所有可能期权组合为1755个。

1、最优化问题的提出

对上述第i个可能的组合期权我们记为Oi，其收取的保证金记为mi，相应的数量记为wi，原编号合约的实际仓位记为Wi，组合合约与编号合约对应的位置矩阵为P，组合所需要的单合约数量为N，则我们关心的最小保证金问题可以写成如下数学问题：

2、组合构建与相关矩阵的计算机生成

以认沽熊市价差策略为例，其需要一个权利仓，一个义务仓，且最终保证金为两者行权价之差，相应的计算机代码为：

对于整型最优化问题，我们采用的是GNU开源项目GLPK①，其可以用来求解线性规划、混合整数规划以及相关的一些问题。

四、实证检验

根据表格4实证结果中2015年4月某日及后续一段时期内的期权持仓信息，可以看到，某一交易日共持有权利仓460手、义务仓387手，合计占用保证金120.79万元。经过组合构建最优化后的持仓组合持仓共计370张，权利仓90张、义务仓17张，合计占用保证金102058.04元，下降幅度约为91.55%，所有运行结果如表4与图1所示。

在普通的i7-5600u cpu电脑上，利用高速的GNU GLPK求解器，在10毫秒内就能对1755个组合合约进行最优化求解，这种计算效率完全可以胜任做市商的实时保证金计算需求。

五、结论及建议

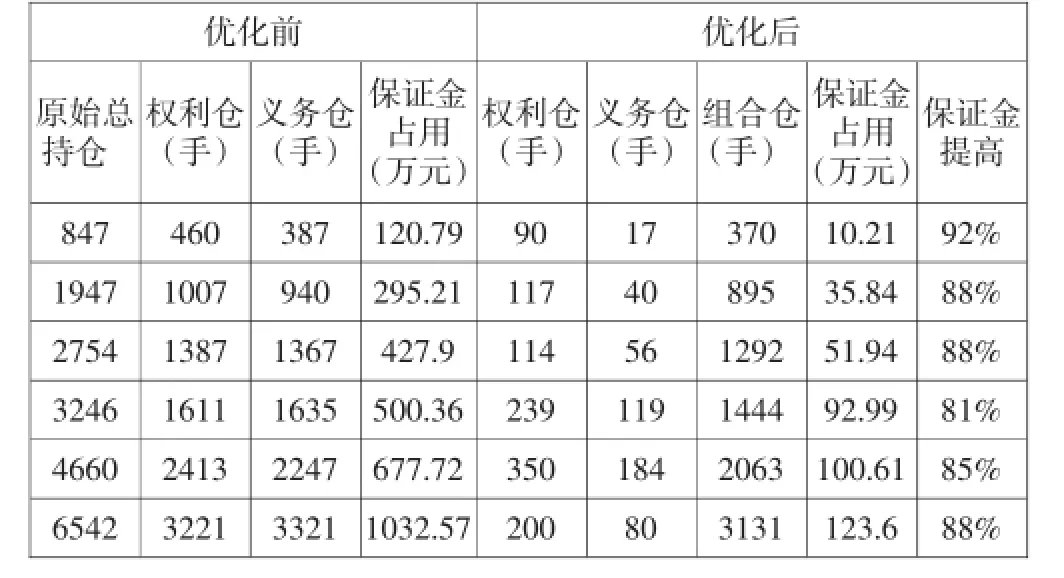
表4 实证结果

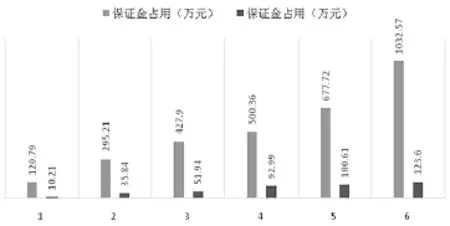
图1 保证金占用情况

组合保证金制度的推出对于普通期权交易者、机构投资者、期权做市商均是大大的利好，能有效改善期权交易中保证金占用过多的问题，提高资本利得率。本文所讨论的保证金最优化模型是基于数学整型最优化理论，在现有期权组合保证金方案制度下，合理利用不同期权间组合从而达到最优化降低保证金占用的目的。从效果看，对于大部分期权做市商和期权投资者，该模型均可以降低80%以上甚至90%的资金使用。

未来随着更多的两腿组合策略，甚至三腿、四腿组合保证金制度的提出，利用本文模型的拓展配合更现代的诸如GPU计算[4]、FGPA计算[5]等计算机手段可以更进一步地快速优化资金利用率、合理配置资产。

注释

① GNU Linear Programming Kit，www.gnu.org/software/ glpk/.

[1] 顾宗源：50ETF期权的推出对我国目前金融市场的影响[J].现代商业，2015（7）.

[2] 上海证券交易所：上海证券交易所股票期权组合策略保证金交易方案[Z].2015.

[3] 上海证券交易所：关于就组合策略保证金交易与结算方案征求意见的通知[Z].2015.

[4] 张庆科、杨波、王琳、朱福祥：基于GPU的现代并行优化算法[J].计算机科学，2012（4）.

[5] Altera公司：利用FPGA加速实现高性能计算[J].电子产品世界，2008（1）.

（责任编辑：张琼芳）