基于SARIMA-GARCH模型的海南省月度CPI预测

（同济大学，上海 200082）

基于SARIMA-GARCH模型的海南省月度CPI预测

王子丰

（同济大学，上海 200082）

稳定物价是政府市场调控的一个重要目标，因此把握CPI的宏观趋势具有一定的现实意义。本文依据海南省2000年1月至2015年12月月度CPI值，运用ARIMA季节模型进行拟合，考虑残差可能的ARCH效应，并对2016年1月至10月的CPI进行了预测。实证表明，ARIMA（2，1，2）（1，0，1）[12]模型能对海南省月度CPI起到较好的预测效果，对于政府政策制定调控市场具有一定的参考价值。

海南省物价指数；ARIMA模型；CPI预测

一、引言

CPI即居民消费价格指数，是反映一定时期内城乡居民所购买的生活消费品和服务项目价格变动趋势和程度的相对数，是对城市居民消费价格指数和农村居民消费价格指数进行综合汇总计算的结果。通过该指数可以观察和分析消费品的零售价格和服务项目价格变动对城乡居民实际生活费支出的影响程度。[1]由于与普通老百姓的生活息息相关，CPI往往是人们最为关心的经济指标之一。政府可以通过CPI全面把握经济发展趋势并及时采取措施调控，因此，建立能准确预测CPI的模型具有一定的现实意义。

目前，国内外有许多学者对CPI预测相关的研究。采取的技术手段非常多，主要有神经网络、灰度预测、时间序列等。其中，时间序列有一套成熟的理论模型用于处理宏观经济数据，已经得到广泛的认可。如文献[2]研究得出ARIMA（1，1，10）对我国的通货膨胀提供了较好的预测[2]；文献[3]得到季节ARIMA模型较为成功地拟合了安徽省的月度CPI，结果比较真实准确地反映了安徽省的CPI变化趋势[3]；文献[4]采用ARIMA-GARCH模型对北京市的月度CPI进行了拟合，与实际拟合较好[4]。

本文依据国家统计局官网公示的海南省2000年1月至2015年12月的月度CPI数据，应用SARIMA模型进行拟合，同时考察残差的ARCH效应，并对2016年1月至10月的CPI数据进行了预测。

二、模型选择

1、季节性自回归移动平均（SARIMA）模型

ARIMA全称为Auto Regressive Integrated Moving Average，其包含AR（自回归），d（差分）及MA（移动平均）三个组成部分，通常的表示方式为ARIMA（p，d，q），p、d、q分别代表自回归、差分和移动平均的阶次。使用ARMA模型的前提为时间序列必须平稳（即在一个不变的均值水平附近保持均衡，没有明显的趋势），然而实际研究中的序列通常是非平稳的，因此通常经过差分使其成为平稳序列。实际运用于季节性时间序列数据时，需要运用乘积模型将季节性ARIMA模型与非季节性ARIMA模型结合，得到ARIMA（p，d，q）（P，D，Q）s，这里P、D、Q分别表示季节性自回归、差分和移动平均的阶数。

对于一般的时间序列zt，其季节性ARIMA模型可用如下数学公式来表示。

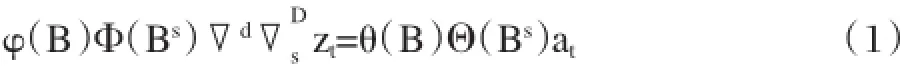
2、广义自回归条件异方差（GARCH）模型

GARCH（p，q）模型的一般形式为：

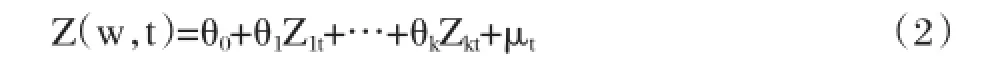
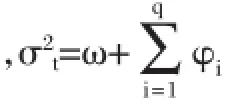
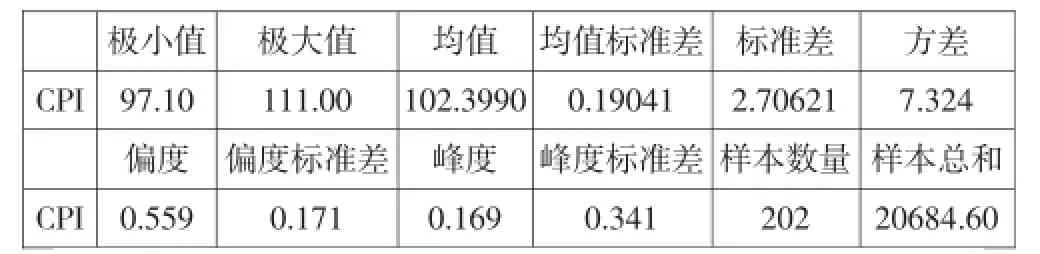
表1 2000/1至2016/10海南省月度CPI数据描述统计量

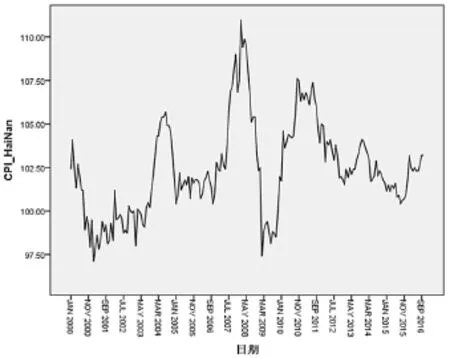
图1 2000年1月至2016年1月海南省月度CPI时间序列图

时间序列的GARCH（p，q）建模，首先进行GARCH（异方差）检验，平稳序列的条件方差为常数值时，即不存在异方差效应时，不必建立GARCH模型；当存在异方差效应时，需建立GARCH模型并估计模型参数，一般采用最小二乘法。而对于联合分布形式已知的时间序列，极大似然估计法更为准确。然后根据AIC准则，确定模型阶数并进行模型预测。由此可避免异方差效应对时间序列模型的影响，提高时间序列模型的预测精度。

三、实证研究

1、模型建立

（1）数据选择。本文选取2000年1月至2016年10月海南省月度CPI数据，以RGuI3.3.2、SPSS20和EVIEWS9.0为平台进行模型实现。分别对原始数据在SPSS中进行描述性统计和时序图刻画。

由表1和图1可知，十余年内海南省的月度CPI波动较大但无明显趋势，新世纪前几年曾经历了一段时间的通货紧缩，而且在2008年和2010年均达到过较高的水平。整体来看，初步判断其为不平稳序列，需要进行对数化处理和差分平稳化。

（2）平稳性分析。对CPI序列在Eviews中进行ADF（单位根）检验，得到结果如图2所示，可知在15.56%的显著性水平下接受原假设，即不能拒绝存在单位根的原假设，说明该序列为非平稳序列。

为得到平稳的序列，对序列取自然对数再进行一阶差分，并再次进行ADF检验，结果见图3。拒绝原假设，认为该数据为平稳序列。所以可以认为原CPI的自然对数序列是一阶单整的，记为I（1）。

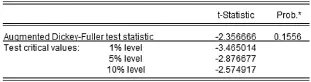
图2 CPI时间序列ADF检验结果

图3 DlogCPI时间序列ADF检验结果

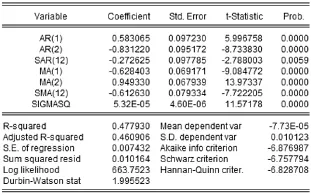
图 4 对 LogCPI进行 ARIMA（2，1，2）（1，0，1）[12]拟合的结果

（3）模型识别。R提供了海量可用于时间序列建模的包，本文使用forecast包中的auto.arima函数对2000/1至2015/12的数据的自然对数logCPI进行模型的识别以确定模型阶数，其根据AIC准则自动探测构 造 了 ARIMA（2，1，2）（1，0，1）[12]模型。将该模型在Eviews中进行拟合，得到结果如图4所示。拟合结果表明，模型的各个参数均显著且其拟合优度较高，说明该模型确实能够较好地描述序列的波动变化。模型可以表示为如下的公式：

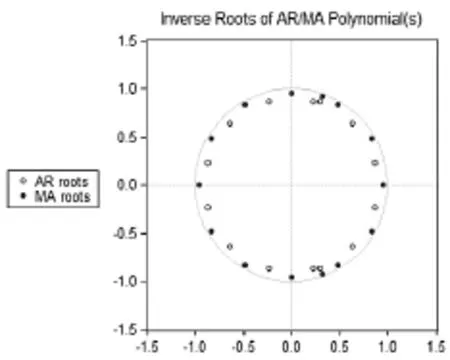
图5 模型平稳性检验结果

2、模型检验

（1）模型平稳性检验。得到ARIMA模型后，重要的一步是检验模型的平稳性，否则模型不具有解释力。对模型系数的特征方程根的倒数画单位圆得到图5，可见特征方程根的倒数均在单位圆内，模型平稳。

（2）残差检验。为了避免可能存在的单模型拟合导致的信息损失，有必要分析残差项之间的自相关性和异方差效应。因此对拟合完成后模型的残差项做ARCH效应检验，结果如图6所示。Heteroskedasticity检验结果说明不能拒绝原假设，即该数据的异方差效应并不显著，不再需要对残差进一步建立GARCH模型。

图6 模型残差序列的ARCH效应检验

根据模型残差的ACF（自相关）和PACF（偏自相关）（见图8）可知，残差序列的自相关和偏自相关系数均显著为0，可以认定残差序列为白噪声序列，即模型已将原始时间序列数据的信息基本提取出来。同时由图7可以看出，模型与原数据非常拟合。

3、模型预测

用模型对2016/1至2016/10的月度CPI进行动态预测，得到结果如表2所示。预测结果显示CPI值在2016年具有一路走高的趋势，与实际趋势一致。除了二月份的相对误差达到1.5%，其余月份的相对误差值均低于0.5%，平均相对误差仅为0.4126%，模型预测的结果比较精确。

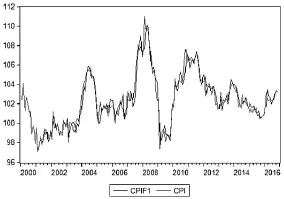
图7 CPI原始序列与预测序列拟合图

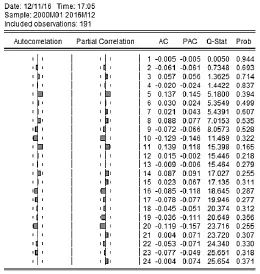
图8 ARIMA（2，1，2）（1，0，1）[12]模型残差ACF& PACF图

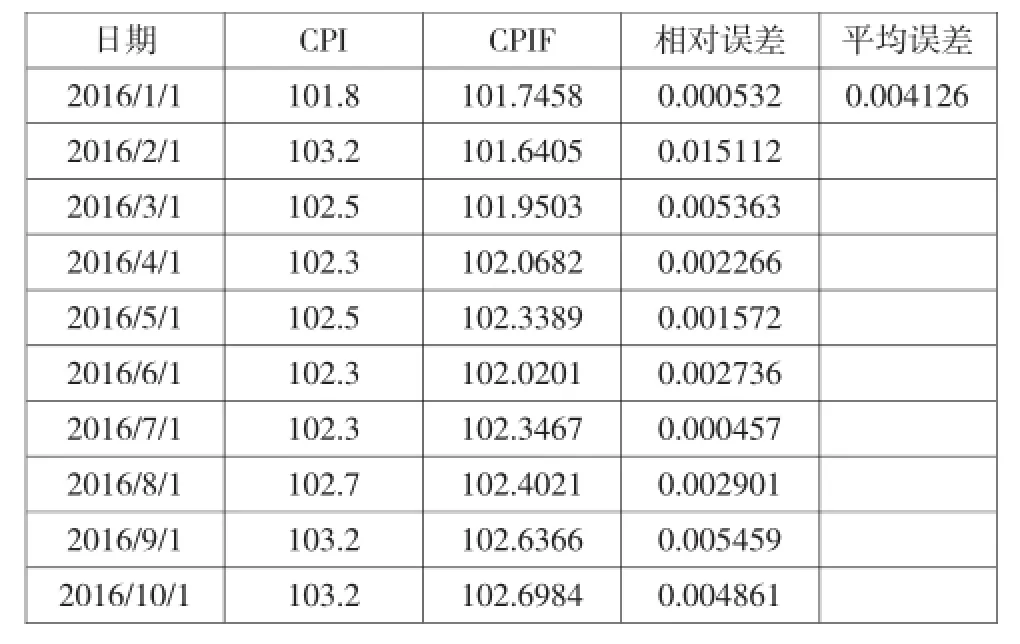
表2 2016年1月至10月的CPI与CPIF对比

四、结论

自2009年国务院《关于推进海南国际旅游岛建设发展的若干意见》颁布后，海南国际旅游岛建设正式上升为国家战略，海南省经济得到快速发展，物价水平也相应提高。从多方面来看，海南价格水平均高于全国一线城市水平，物价调控任务艰巨[5]。相对于海南较高的物价水平，海南本地居民收入与其并不相匹配。在这种情况下，政府面临着调控通胀，保持居民生活水平的艰巨任务。实证表明，ARIMA（2，1，2）（1，0，1）[12]模型为海南省CPI提供了较优的预测。政府可以通过对CPI走势的有效预期，变被动为主动，及时出台调控政策，以达到稳定市场预期的目标，使海南省的旅游业发展切实造福大众。

[1] 国家统计局：价格指数[EB/OL].http：//www.stats.gov.cn/ tjsj/zbjs/201310/t20131029_449518.html.

[2] 肖曼君：中国的通货膨胀预测：基于ARIMA模型的实证分析[J].上海金融，2008（8）.

[3] 王扬眉等：基于季节ARIMA模型的安徽省CPI预测[J].价格月刊，2012（8）.

[4] 张小燕：北京市的CPI时间序列分析及预测[J].商情，2012（22）.

[5] 毕普云：海南物价形成机制研究[J].海南师范大学学报（社会科学版），2014，27（10）.

（责任编辑：刘冰冰）