理解定义关联概念,解后反思走向教学
——一道新定义考题的思路突破与教学思考
2017-04-24河南省郸城县教研室于杰
☉河南省郸城县教研室 于杰
☉河南省郸城县第二高级中学
理解定义关联概念,解后反思走向教学
——一道新定义考题的思路突破与教学思考
☉河南省郸城县教研室 于杰
☉河南省郸城县第二高级中学
当前流行的函数综合题多是以常见的函数图像(直线、曲线、抛物线)为背景,融入几何基本图形进行一些演算或推证,难点往往在几何构造,与函数的性质或本质甚至没有直接相关性,使得不少命题研究者将上述试题归到所谓“伪坐标系”“伪函数题”.本文结合一道北京海淀区中考模考的新定义题,讲解思路突破,反思问题结构,并跟进教学思考,供研讨.为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为0.例如,图1中的函数有0、1两个不变值,其不变长度q等于1.
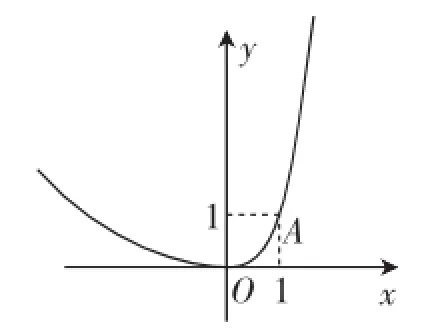
图1

图2
一、考题及思路突破
考题:(2016年北京海淀区中考二模,第29题)对于某一函数给出如下定义:若存在实数p,当其自变量的值
(2)已知函数y=2x2-bx.
①若其不变长度为0,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3)记函数y=x2-2x(x≥m)的图像为G1,将G1沿直线x=m翻折后得到的函数图像记为G2.函数G的图像由G1和G2两部分组成,若其不变长度q满足0≤q≤3,分析m的取值范围.
理解新定义:在开始求解具体问题时,我们先对所谓的新定义进行直观理解,构造图2分析,作出直线y=x,与原函数图像相交于点O(0,0)、A(1,1).这样新定义提及的所谓不变长度就是两点纵坐标的差|yA-yO|=1-0=1.我们用初中生熟悉的数学符号语言将问题重新表述之后,有利于后面思路的讲解与突破.
思路突破:
(1)有了上面的准备工作,我们就可构造出图3~图5直观理解,直接看出答案:函数y=x-1没有不变值;函数有-1和1两个不变值,其不变长度为2;函数y=x2有0和1两个不变值,其不变长度为1.
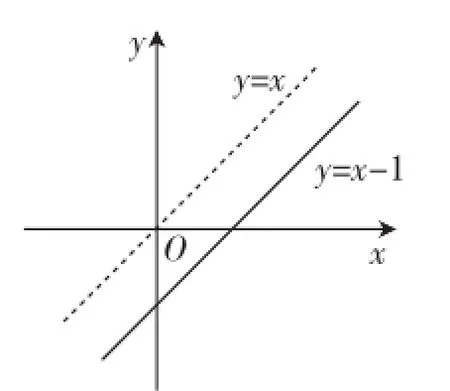
图3
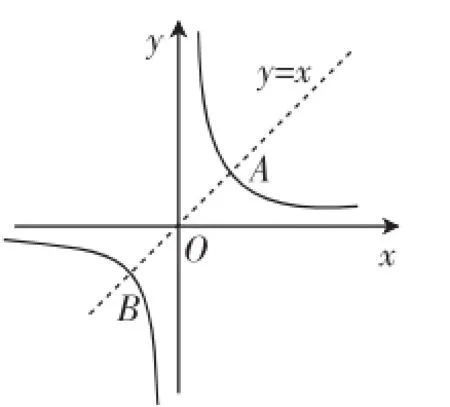
图4
当然,我们也可“离开”图形,从“数”的角度算出答案.比如,函数y= x-1与直线y=x联立得方程组该方程组无解;类似的,联立得方程组可得交点(1,1)或(-1,
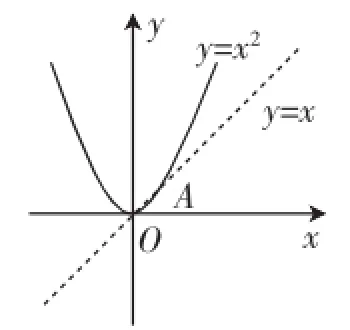
图5
(2)①函数y=2x2-bx的不变长度为0,就是将其与直线y=x联立后的方程组有两组相等的实数解,即一元二次方程2x2-bx=x有两个相等的实数根,根据Δ= 0可解出b=-1.此时抛物线y=2x2+x与直线y=x有且只有一个公共点(0,0),符合不变长度为0的要求.

由1≤b≤3,得1≤x2≤2.不变长度为x2-x1,代入x2的极值,可分析出y=2x2-bx的不变长度q的取值范围为1≤q≤2.
(3)首先想清楚抛物线y=x2-2x与直线y=x交于点O(0,0)及A(3,3),这样我们就可依次构造出图6~9的可能情况,注意图象的虚像与实数是由自变量x≥m及对称(沿直线x=m翻折)后的实像与虚像.
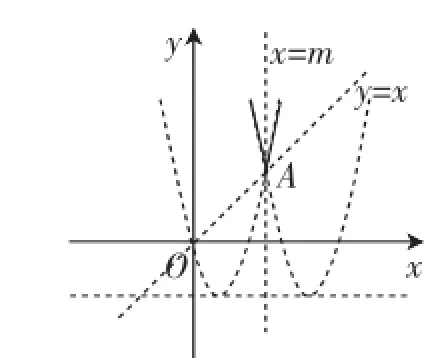
图6
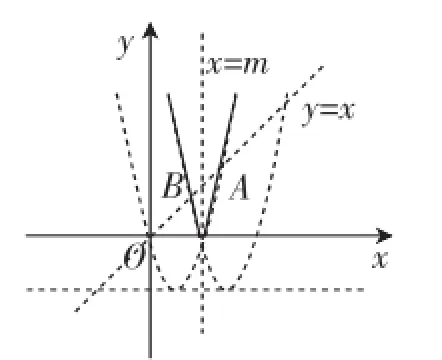
图7
在图6中,当m=3时,可见到此时新图像G(两个实像分支组合而成)与直线y=x恰交于一点A(3,3),此时不变长度q为0.符合要求(0≤q≤3).想象将直线x=m向右平移(m>3),则新图像G与直线y=x就没有交点了,说明m>3时不合题意.
接下来将直线x=m向左平移,如图7所示,1≤m<3时,新图像G与y=x交于点A(3,3),还有另一点B,在线段AO上,显然此时不变长度q满足0≤q≤3,故1≤m≤3符合要求.
接着将直线x=m向左平移,0≤m≤1时,如图8,新图像G与y=x交于点A(3,3),还有另一点C,在AO的延长线上,此时q>3,与0≤q≤3矛盾.
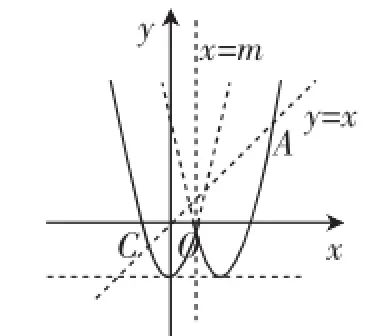
图8
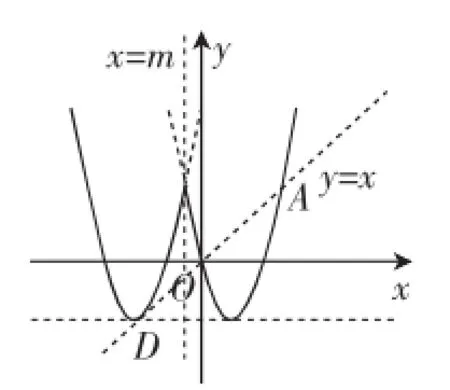
图9
继续将直线x=m向左平移,如图9,可以想见翻折后的抛物线与直线y=x有一次相切的情况(图9中点D),此时设该抛物线的解析式为y=(x-n)2-1,易得n=-,即此时y=(x+)2-1,根据对称性,此时m=-;就是说,此时不变长度q对应着A、D两点的纵坐标之差,不符合0≤q≤3的要求.而当直线x=m继续向左平移时,新图像G左侧部分与直线y=x就没有交点了,这样不变长度q又回到A、O两点之间的纵坐标之差,符合要求.则m<-符合题意.
解后反思:这道新定义考题除了表述新定义时附了一个简单的图形,下设小问都没有给出图像,但是我们却可以根据题意构造出丰富的图像辅助理解,体现了以形助数的解法特点,特别是最后一问,需要结合直线x= m的位置,想清楚虚像、实像,并理解实像与直线y=x的交点的意义,这样考查思考、函数图像性质的考题较好地达到了“多想少算”的命题风格,值得点赞.
二、关于新定义考题的教学思考
在近几年北京中考试题的引领下,北京各区七、八、九年级的把关题都积极跟进,出现了大量优秀的新定义考题,引领了教学方向,重在启发学生思考,学会思维,理解数学概念的本质,以下再围绕新定义考题的教学,提出一些初步的思考.
1.学会阅读并准确理解新定义是成功解题的起点.
新定义考题开始的几段话或几句话都是阐释新定义的内容,并会辅以必要的例子、图形来解释新定义,就像数学上很多描述性定义一样(比如,形如……的式子称为分式).在解答新定义考题时,不要急着看后续设问,而应该在阅读理解新定义语句、字符时下足功夫,做到读懂、读通、读顺新定义中的每一个字句、每一个字符、图形上的每个线条的特点、字母的特点、位置的特点等.我们见到不少同学不能顺畅解答新定义考题,往往是对总题干中的新定义没有能准确理解所致.
2.善于将新定义相关概念与所学概念关联、对比.
新定义考题常常是初中阶段所学的一些概念穿靴戴帽、乔装改扮而来,在阅读理解新定义后,要结合题干中所举的例子、图形认真分析,发现所谓新定义与此前初中数学哪一个数学概念、数学性质有关联,关联在何处.比如,上面考题新定义的本质就与一次函数中正比例函数y=x相一致,只是包装了一个说法而已,接下来对于不同形式的函数,只要将其与y=x联立成方程组解出它的解即可继续分析.
3.解函数类新定义题要注重“数形结合”的分析策略.
本文述及的考题是一道函数类新定义题,下设几个小问虽然没有给定图像,但是解题时心中要有图形意识,我们在上文中构造出多个图形就是想传递数形结合分析策略,因为直观的图像理解有助于对问题的思考,也是符合函数本质的(函数的关系就是沟通数形关系).特别是考题的最后一问,我们构造了图6~图9,试图从动态的角度直观发现图像G与直线y=x的交点情况,最容易忽略的就是图9中有一次相切的情形,而这又对应着一元二次方程根的判别式为0.为了帮助学生更好地从数形结合的角度分析最后一问,教学时可设计出如下的一些提示问题:
问题1:当m=1时,画出函数G的图象;
问题2:当m=3时,指出函数G的图像与直线y=x的交点坐标;
问题3:当m=-1时,指出函数G的不变长度q;
问题4:函数G的不变长度q满足0≤q≤3,分析m的取值范围.
四、写在后面
近年来在《中学数学(下)》见到一些新定义考题的教学研讨文章,多数集中在解法探讨,深入到如何开展新定义考题的教学设计,让更多优秀的、抽象的新定义考题能以更生动、形象的面貌呈现在课堂上,我们要做的研究还很多,本文只是由一道新定义考题述及一些初步思考,做得还不够,期待今后继续努力,研发新定义考题的“一题一课”.
1.甘晓云.以退为进:挑战新定义考题的有效策略——北京海淀九上期末卷第29题解析与赏析[J].中学数学(下),2017(2).
2.许燕.从解题赏析走向教学研究—以2016年无锡卷第27题为例[J].中学数学(下),2016(10).
3.秦怡.回到概念,让解题念头“自然生成”——从一道几何难题的思路突破说起[J].中学数学(下),2017(2).
4.郑毓信.“开放的数学教学”新探[J].中学数学月刊,2007(7).
