基于“数学核心素养”视角下的解题教学*——从波利亚解题思想出发

☉华中师范大学数学与统计学学院 魏珂

☉华中师范大学数学与统计学学院 胡典顺

基于“数学核心素养”视角下的解题教学*
——从波利亚解题思想出发

☉华中师范大学数学与统计学学院 魏珂

☉华中师范大学数学与统计学学院 胡典顺

一、背景引入

2014年3月30日，《教育部关于全面深化课程改革落实立德树人根本任务的意见》颁布后，“数学核心素养”一词迅速引起数学教育界的热议.一般认为，六大数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.六大数学核心素养是一个相互独立又相互交融的有机整体，数学核心素养不仅能衡量一个中学生的数学综合能力，也是帮助中学生发现数学问题、进行数学解题、归纳数学结论的重要素养.因此，如何培养初中生的数学核心素养并将其运用于解题教学是当今数学教育界值得重视的一个问题.

美国著名数学家、数学教育家乔治·波利亚（George Polya，1887—1985）一生中在数学界众多领域都作出了开创性的贡献，著名代表作《怎样解题》对中学数学教育产生了极大的影响.他的解题思想集中体现在他创立的“怎样解题表”中，他将解题过程分为四个阶段，即：理解题目、拟定方案、执行方案、回顾.

下面，笔者以一道中考几何题为例，在波利亚“怎样解题表”的框架下，对六大数学核心素养如何在各阶段发挥作用并引导解题展开分析.

二、解题分析

（2016福建福州，25）如图1，△ABC中，∠A=30°，AB=AC，以B为圆心、BC长为半径画弧，交AC于点D，交AB于点E.

（1）求∠ABD的度数；

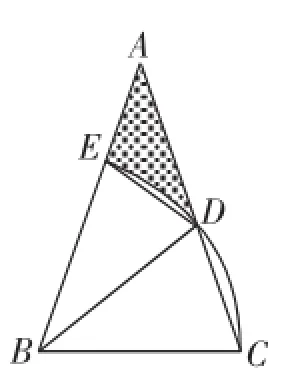
图1

1.理解题目阶段.

理解题目即审题.在审题阶段，可以通过数学抽象素养，将已知信息具体化，可以引导出隐含信息，通过直观想象素养对给出的图形进行分析和发现，再通过数据分析素养引导解题的方向.

分析：就本题而言，对于第（1）问，从题目中的已知条件“AB=AC”可以抽象出隐含条件“△ABC是等腰三角形”，从“以B为圆心、BC长为半径画弧”可以抽象出隐含条件“BD=BC”，再通过对已知数据的分析，即可为“求出∠ABD的度数”作准备.对于第（2）问，题目中的隐含条件有“以B为圆心、BC长为半径画弧”，再通过观察图形，运用直观想象素养引导，容易看出所求阴影部分与△AED和扇形BED有关系，如图2所示，从而确定第（2）问的解题思路.

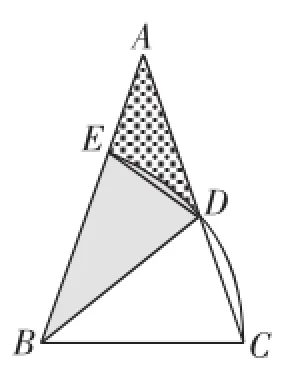
图2

2.拟定方案阶段.

审题结束后，即进入分析所有条件并拟定解题方案阶段.主要运用逻辑推理、数学建模、直观想象、数学运算素养引导拟定解题方案.

分析：对于第（1）问，运用逻辑推理素养，可以找到未知角∠ABD与∠ABC之间的关系“∠ABD=∠ABC-∠DBC”，再运用数学建模素养确定逻辑严谨的解题方向和方案：由理解题目阶段发现的隐含条件“△ABC是等腰三角形”和已知条件“∠A=30°”可以通过数学运算求出∠ABC和∠BCD的度数；再通过隐含条件“BC=BD”容易求出∠DBC的度数，从而求出未知角∠ABD的度数.对于第（2）问，从理解题目阶段运用直观想象素养分析可知“S阴影=S△ABD-S扇形BDE”，从题中的已知条件“BD=”并运用扇形面积公式容易求出扇形BDE的面积，这一问的难点就在于求△ABD的面积.由于AB×高，通过直观想象素养的引导，可以看出这里需要构造辅助线，即△ABD的边AB上的高DF（如图3所示）.最后通过逻辑推理和数学运算我们可以根据已知条件BD=和第（1）问中求出的∠ABD的度数求出AB和DF的长度，从而△ABD的面积可以求出.

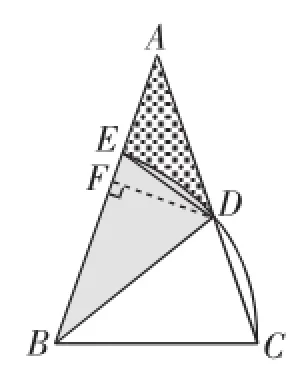
图3

3.执行方案阶段.

拟定方案结束后进入执行方案阶段.本阶段主要运用数学运算素养和逻辑推理素养对解题过程进行书写.

分析：对于第（1）问，因为AB=AC，∠A=30°，所以∠ABC=∠ACB=75°.由已知条件知BC=BD，所以∠BDC=∠BCD=75°，∠DBC=30°，从而∠ABD=∠ABC-∠DBC= 45°.

对于第（2）问，过点D作DF⊥AB于F.在Rt△BDF中，∠FBD=45°，BD=BC=，所以BF=DF=BD·sin45°==1.在Rt△ADF中，∠A=30°，所以AD=2DF= 2，AF=，所以AB=AF+BF=+1.所以S阴影=S△ABD-

4.回顾阶段.

这道题是对初中几何中“三角形”及“扇形”的考查，因此在回顾阶段可以利用三角形和扇形的基本性质进行检查反思.

分析：首先，要利用数学建模素养、直观想象素养和逻辑推理素养对这道题的解题思路和解题方案进行整体梳理；其次，对题目中的隐含条件和结论数据进行分析和检验，看是否符合实际情况，这里既需要数学抽象素养的引导，也需要数据分析和数学运算素养的运用.对于第（2）问，也要对三角形和扇形的面积公式进行检查，并对计算出的数据检验和分析，看数据结果是否合理.这道题的难点之一就是运用直观想象素养将第（2）问中要求的阴影面积转化成另外两个图形的面积差，通过体会这一过程的发现，真正掌握解决此类问题的方法和技巧.可以看出，在回顾的过程中，六大核心素养都发挥了一定的引导作用，因此回顾阶段是综合提高学生数学核心素养的有效途径，不容忽视.

三、六大核心素养在解题教学中的运用

1.运用数学抽象发掘信息.

数学抽象是指舍去事物中的一切物理属性，得到数学研究对象的素养.通常在理解题目阶段运用数学抽象素养对题目中的隐含条件和信息进行发掘，将抽象变具体，将隐含变清晰.以上面这道中考题为例，通过数学抽象素养可以从题目中的已知条件“AB=AC”发掘出隐含条件，即“△ABC是等腰三角形”，这对问题的解决是至关重要的第一步.

2.运用数据分析找出本质.

数据分析是指针对研究对象获取数据，运用统计、计算等方法对数据进行整理、分析和推断，形成关于研究对象知识的素养.题目中的图表或数据往往有着内在的联系并隐含着重要的信息，在理解题目的过程中，可运用数据分析素养引导和分析已知数据，通过整理数据，找出问题的本质，从而解决问题.比如，将这道中考题中的已知数据“∠A=30°”与已知条件结合起来分析，就是第（1）问的求解的关键所在.

3.运用直观想象发现思路.

直观想象是借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的素养.通过建立数与形的关系，引导学生建立数学解题的直观模型，再运用逻辑推理和数学建模探索解决问题的思路和模型.比如，这道中考题的第（2）问无法直接求解，通过直观想象素养的运用可以看出图形面积之间的关系，从而作出辅助线，发现解题思路.

4.运用逻辑推理探索思路.

逻辑推理是指从一些事实和命题出发，依据规则推理出其他命题的素养.逻辑推理是解题中的基本思维品质，既要保证解题的严谨性，又要把握事物之间的关联并引导出进一步的解题思路.逻辑推理一般运用于拟定方案和执行方案的过程中，即对解题过程的书写，不仅要用正确的公式或文字进行表达，头脑中还要通过逻辑推理素养对整个解题思路进行一步步推理与探索，从而完成解题.

5.运用数学建模设计方案.

数学建模是对现实问题进行数学抽象，用数学语言表达问题，用数学知识与方法构建模型解决问题的素养.数学模型的搭建是数学解题的重要形式，也是解决实际问题的基本手段.通过数学模型的建构引导，设计出解题方案，为下一阶段的执行方案奠定基础.数学建模素养主要运用于拟定方案阶段，通过对逻辑推理出的思路进行整理和建构，在头脑中设计出一个完整的解题模式和方案，为下一步的书写和计算打下良好的基础.

6.运用数学运算得出结果.

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.只有具备了一定的数学运算素养，才能依据已经建立的数学模型和数学思路引导运算进而得出结论.因此，数学运算素养在解题过程中也是至关重要的，它不仅贯穿于整个解题过程，而且在执行方案和回顾阶段发挥着重要的作用，也是整个题目的结论是否正确的关键所在.

四、在解题教学中培养“数学核心素养”的建议与思考

1.加强概念教学，强化数学抽象.

在初中解题教学中，想要提高数学抽象素养就应该重视题目中基本概念的提取.比如，上文这道中考几何题中的基本概念就是“三角形”和“扇形”.学生只有理解了这两个基本概念，并通过找出这些概念和图形的内涵和外延，结合概念的一些特殊性质，才能抽象出题目的深层含义.当然，基本概念的提取离不开平时课堂中的概念教学，因此，要想很好地培养学生在解题中的数学抽象素养，就应该加强初中阶段的概念教学，在教学过程中重视对基本概念的积累与记忆，让学生学会在解题中提炼基本概念，从而简化条件找到本质.

2.重视计算训练，提高运算分析.

在初中解题教学中，可以通过对学生计算能力的锻炼提高学生的数学运算素养和数据分析素养.在解题教学过程中，要让学生从理解运算的基本知识出发形成一定的运算技能，可以采用“先慢后快”的原则，即刚开始练习时运算步骤和依据必须明确、清晰，运算过程必须规范，待学生熟练后可适当加快运算速度或简化步骤.另外，还可以通过引导学生对运算规律和基本类型进行分类整理，使学生头脑中建构出完善的运算知识系统，最终达到加快解题速度和提高正确率的效果.当然，这些题目最好具有一定的规律性和趣味性，也可以作为思考题留给学生课下进行思考，从而使学生的数学运算素养和数据分析素养得到潜移默化的提升.

3.强调数形结合，提升直观想象.

在初中解题教学过程中，对学生直观想象素养的培养可以从以下几个方面进行.第一，在教学过程中注重基本图形的理解和积累.一般来说，任何一个几何问题都是由基本图形组成的，在解题过程中如果学生看到一个几何图形时能够快速观察、发现、分解出它蕴含的基本图形，无疑能达到事半功倍的解题效果.第二，让学生体会并学习数形结合的思想和方法.如果学生学会了在解题时尽可能用画图来解决问题，化数为形，将代数问题与几何问题联系起来，找到本质，就可使复杂的问题简单化.第三，利用多媒体教学化静为动.像几何画板、超级画板Z+Z、GeoGebra、3D数学教学平台等动态几何软件，有助于教师生动、形象地展示几何图形的各种性质和演示几何变化的动态效果，带给学生直观视觉上的冲击，有利于培养学生观察、认识周围事物间的数量关系和形体特征的兴趣和意识.

4.注重逻辑练习，锻炼推理能力.

提高学生的逻辑推理素养对数学解题也是很有必要的.对学生逻辑推理素养的培养能够保证学生在解题时的正确性和严谨性，在教学过程中可以通过对类比法、分析法（包括逆证法）、综合法、反证法、归纳法、穷举法（要求分类讨论）等逻辑数学方法的讲解对学生的逻辑推理素养进行有意识培养，并通过一些逻辑思维的练习题进一步提升学生的逻辑推理素养.

5.生活联系实际，建构数学模型.

数学建模，顾名思义就是要培养学生对数学模型的建立，这一素养的培养来源于生活又高于生活.在教学过程中可以将现实生活中与数学学习有关的素材引入课堂，通过一定的趣味性满足学生好奇的心理要求，从而在学生头脑中建立起一个个数学模型，从而方便他们在解题中使用并建立相关模型.通过建立模型全面理解题目并引导设计解题方案，达到解题目的.

1.G·波利亚著.涂泓，冯承天译.怎样解题［M］.上海：上海科技教育出版社，2011.

2.朱立明.基于深化课程改革的数学核心素养体系构建［J］.中国教育学刊，2016（5）.

3.刘锦，李龙安，侯学萍.基于核心素养导向的中学数学教学思考［J］.现代中小学教育，2016（10）.

全国教育科学规划教育部重点课题——TPACK视角下卓越教师培养的理论研究与实践探索（课题编号DHA150287）.