有理数的进一步研究和探索——以中美初中数学教材比较为基础

☉甘肃酒泉第四中学徐玉庆

有理数的进一步研究和探索
——以中美初中数学教材比较为基础

☉甘肃酒泉第四中学徐玉庆

笔者2016年9月在《中学数学（下）》发表了《中美两国初中数学教材的比较研究——以“有理数”为例》，其中比较了国内人教版、北师大版和美国教材中对于有理数的定义及有理数的有关运算，发现对于有理数的定义人教版和北师大版是完全一样的，都是将整数和分数统称为有理数，而美国教材（Glencoe/McGraw-Hill California Mathematics）则将有理数定义为：Numbers that can be written as fractions are called rational numbers（只要能够表示为分数的数称为有理数），Since：-7可以表示为-，2可以表示为，0.1可以表示为，其中循 环小数也可以表示为分数.之后的教学过程中，我不断思考这两种定义，不断研究美国教材，不断研究国内其他版本的初中数学教材，发现苏教版、鲁教版、冀教版和人教版、北师大版教材中对于有理数的定义如出一辙，于是笔者不断思考这两种定义方式对于学生理解有理数的定义有着怎样的不同，由此笔者对有理数开展了一次全面的探索和比较.

一、有理数的历史

有理数在希腊文中称为λογοξ，原意是“成比例的数”.英文取其意，以ratio为字根，在字尾加上-nal构成形容词，全名为rational number，直译成汉语即是“可比数”.对应地，无理数则为“不可比数”.并非中文翻译不恰当.有理数这一概念最早源自西方《几何原本》，在中国明代，从西方传入，而从中国传入日本时，出现了错误.明末数学家徐光启和学者利玛窦翻译《几何原本》前6卷时的底本是拉丁文.他们将这个词（“λογοξ”）译为“理”，这个“理”指的是“比值”.日本在明治维新以前，欧美数学典籍的译本多半采用中国文言文的译本.日本学者将中国文言文中的“理”直接翻译成了理，而不是文言文所解释的“比值”.后来，日本学者直接用错误的理解翻译出了“有理数”和“无理数”.当有理数从日本传回中国时又延续错误.清末中国派留学生到日本，将此名词传回中国，导致现在中日两国都用“有理数”和“无理数”的说法.可见，由于当年日本学者对中国文言文的理解不到位，才出现了今天的误译.

数学上将有理数定义为一个整数和一个非零整数的比值，表示为（b≠0），19世纪，德国数学家康托尔提出集合的概念，提出了康托尔集.随着现代集合论的不断发展，有理数也在集合论的基础上进行了定义，表示为Q，定义为：｝。现代数学以集合论为基础，有理数集在高等代数中也有许多非常重要的结论.

二、两国教材有理数定义的比较

随着新课改的不断深入，国内出现了现在的一个课程标准，多个版本的初中数学教材，使用比较广泛的有人教版、北师大版、苏教版、鲁教版、冀教版等五大版本.其中有理数的定义都出现在七年级上册第一章：有理数.国内这五种版本的教材对有理数的分类和定义是一致的，如下：

图1

整数和分数统称为有理数.之后教材中对于有理数没有更多的补充和讲解，教材之后的内容就是关于有理数的有关运算.

相比之下，美国教材在七年级上册第一章第一节专门讲解了整数及其运算，第二节才开始引入有理数的定义及其运算，并对概念做了进一步的完善和补充，如图2：

图2美国加州教材有理数的定义

可以发现，美国加州数学教材对于有理数的定义和数学历史上的定义是完全一致的，在第一章第二节中美国教材对于如何将一个整数、有限小数、无限循环小数化为（b≠0）进行了详实的讲解，并附有各种类型的练习，习题的数量要远远多于国内这五种版本教材中习题的数量，许多习题都和现实生活有紧密的联系，相比之下，国内教材中的习题都是不含背景的计算.

那么，这两种定义对于学生理解有理数到底有着怎样的不同？首先，美国教材对于有理数的定义更像是对某个概念的定义，而国内的教材还可以理解为整数和分数都是有理数，这种定义是笼统的、不严谨的.学生在理解的过程中会出现不同的疑问，如：0.125、5.6·、3.267这些数是有理数还是什么？如何进行辨别？在教学过程中发现，教师在讲解了有理数的定义之后，对有理数的定义进行补充，而这些补充的内容在数学教材中并没有涉及，然而在教材后面的习题中又涉及了相关的题目，学生一脸茫然.所以在教学的过程中，教师又添加了有限小数和无限循环小数也是有理数这一结论，因为它们都可以化为（b≠0）的形式.但是在实际教学过程中，我们发现这样的补充效果并不是很好，即使到了七年级下半学期，甚至学生学习了无理数之后，他们对于有理数的理解还是存在问题，这种结果主要是由定义引发的，学生看见形如0.134、3.这样的数，如果从定义出发，第一步要把0.314化为分数，然后根据定义分数是有理数，将0.314归类为有理数，对于3.这样的循环小数不知所措，虽然教师在讲完有理数之后补充了无限循环小数是有理数的内容，但是学生并不能很快地将它归为有理数，这时有理数的定义反而变成一种干扰，对于学生理解有理数的定义是一种负迁移，在概念之间造成了混乱，如果按照美国加州教材的定义，就不会出现这样的问题，因为在第一章第二节中，学生已经在教师的指导下掌握了如何将一个整数、有限小数、无限循环小数化为（b≠0）的形式，所以对于后面的习题，学生直接的方法就是看能不能将一个数化为（b≠0）这样的分数，如果能，这个数就是有理数，如果不能，这个数就不是有理数，减少了学生思维的跳跃和推理，使得问题直接化、标准化.在教学中发现，学生到了八年级学习完无理数之后，对于所学过的整数、分数、有理数、无理数的认识也是模糊不清的，对于有限小数、无限循环小数、无限不循环小数的认识也是模糊不清的，经常在分类中出现错误，如下题：

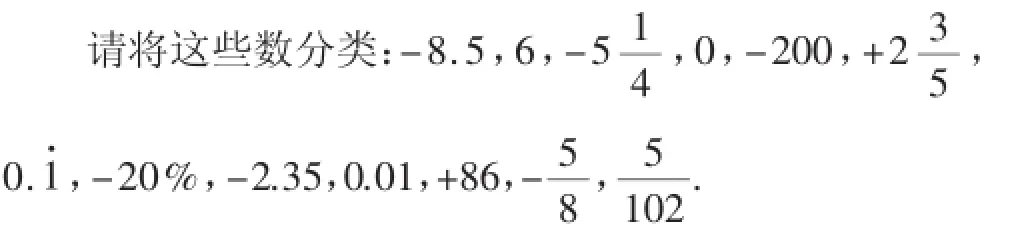
（1）正整数集合｛｝；

（2）负正数集合｛｝；

（3）正分数集合｛｝；

（4）负分数集合｛｝；

（5）整数集合｛｝；

（6）分数集合｛｝；

（7）正有理数集合｛｝；

（8）负有理数集合｛｝.

学生在分类中出现错误最多的是：将有限小数、带分数、无限循环小数分类错误，在教学中教师也反复讲解、反复练习，但实际效果并不是很好.之所以出现这样的结果，原因是教材中有理数定义在学生头脑中先入为主.

三、启示

新的课程改革在国内已经开展了很长时间，教学资源和教学技术也在不断更新，学生有不同的渠道获得知识，如今的反转课堂、慕课已经走在了课堂改革的前列.但是教材在课堂教学中的作用依然非常重要，它使学生能够在较短时间内系统掌握人类文化的结晶，给学生提供一种思路和框架，教材在课程改革中的地位也在不断提升，许多国家开展了大规模的教材研究，2014年在英国南安普顿大学举办了首届国际数学教材研究和发展会议（ICMT-1），吸引了约三十个国家和地区的一百八十余人参加.第二届国际数学教材研究和发展会议将于2017年在巴西举行，第三届也已计划于2019年在德国举行.可见国际数学教育界对数学教材研究给予了前所未有的关注.国内学者也对教材开展了不同程度的研究，但是国内教材研究起步相对较迟，研究范围相对窄小，缺乏专门的研究团队，和西方国家存在一定的差距.这种差距也是一种文化影响的结果，是一种经济和科技发展的结果.课程改革最核心的工作是教材改革，它将直接影响教材所传递的国家意志和民族文化，数学作为衡量一个国家综合国力的指标，数学教育也是衡量一个国家综合素质的指标.通过对有理数的定义的国际比较，我们发现了这种差距.既然有理数的定义在传入中国时已经发生了错误，那么在新的课程改革中是不是可以把这个曾经的“错误”改过来，恢复它的真实面貌？在教材的编排和设计中是不是也应该借鉴国外教材，使课程改革落地生根，蔓延整个神州大地，让教材使用者真正体会到课程改革的力度和效度.

1.中华人民共和国教育部制订.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.义务教育课程标准试验教科书·数学·七年级（上册）［M］.北京：北京师范大学出版社，2014.

3.义务教育课程标准试验教科书·数学·七年级（上册）［M］.北京：人民教育出版社，2014.

4.Rae Young Kim.The quality of non-textual elements in mathematics textbooks：an exp loratory comparison between South Korea and the United States［J］.ZDM-Mathematics Education，2012，44（2）.

5.徐玉庆.中美两国初中数学教材的比较研究——以“有理数”为例［J］.中学数学（下），2016（9）.

6.范良火，熊斌，李秋节.现代数学教育中的教材研究：“概念”“问题”和“方法”［J］.数学教育学报，2016，25（5）.

7.曹一鸣.初中数学教材难易程度的国际比较研究［J］.数学教育学报，2015，24（4）.