借“题”发挥以“变”促学——初中数学课本习题的变式与拓展例谈

☉江苏东台市教育局教研室周玉俊

借“题”发挥以“变”促学
——初中数学课本习题的变式与拓展例谈

☉江苏东台市教育局教研室周玉俊

“变形计”是湖南卫视精心打造的一档生活类角色互换节目，旨在通过人物的角色变换，体验对方的不同生活，实现思想观念上的彻底改变.在数学上，一类源于课本的例题、习题，也可以经过“变形”，蜕变自己，从而更好地发挥其潜在价值，让学生接受一次思维上的洗礼与提升.

一、变形背景

2016年11月，东台市举行了一次全市初中数学命题比赛，在仅提供初中数学课本的前提下，参赛者在半天时间内原创主观题，要求突出考查学生的思维能力和学科素养，体现新课程要求，提供试题答案和命题意图.笔者有幸参与了活动的组织和评委工作，受益匪浅.现呈现三道变形题，与大家共赏.

二、变形内容

1.变形1.

（1）原题回放.

（苏科版教材九年级下册第90页复习题11）如图1，△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，BC分别与AD、AE相交于点F、G.图中有哪几对相似三角形？请把它们表示出来，并说明理由.

图1

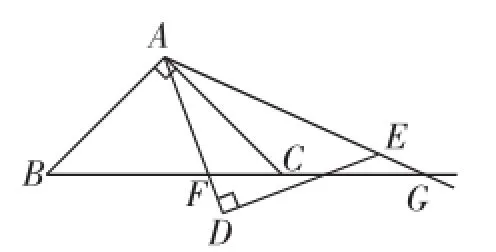
图2

（2）新题赏玩.

如图1，△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，把两个三角形放在同一平面内，使△DEA绕点A旋转，直线BC分别与直线AD、AE相交于点F、G.

（1）如图1，当点F、G在线段BC上时，求证：△ABG∽△FCA.

（2）如图2，把△DEA旋转至图2所示位置，使点F在线段BC上，点G在线段BC的延长线上，设AB=AC=DE= DA=1，FC的长为x，BG的长为y，试求y与x之间的函数关系，并指出x的取值范围.

（3）把△DEA旋转至图3所在位置，试补全图形，标出相应字母，此时（2）中y与x之间的函数关系是否仍然成立？试说明理由.

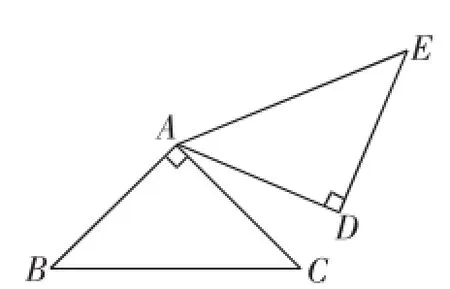
图3

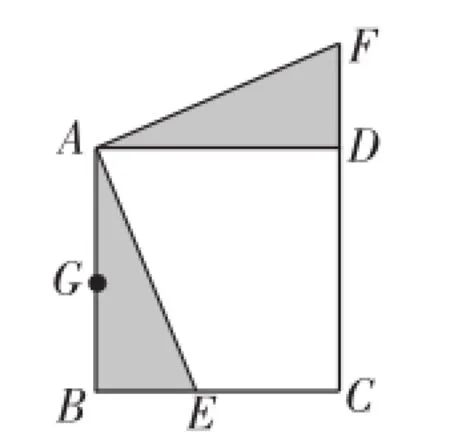
图4

（3）变题意图.

原题中相似三角形对数较多，且有些说明方法雷同，知识点的考查比较单一.改编题第（1）小题是在原题的基础上，选取了其中一对加以证明，对原题进行了简化；第（2）小题是以图1为基础，通过旋转变换将G点放在了BC的延长线上，此时，图形的位置发生了改变，但△ABG∽△FCA的数学本质没有变化，考查学生类比迁移知识的能力，为了增加题目的探究性和综合性，题目又增加了对边长之间关系的探究，综合了反比例函数的知识，其中，对x的取值范围的探究体现了较高的能力要求；第（3）小题以旋转为主线，考查学生动手画图的能力和不同位置条件下迁移和运用知识的能力.题目注重能力立意，小题的设置有梯度，有一定难度，考查学生思维的严密性和灵活性.

2.变形2.

（1）原题回放.

原题1：（苏科版初中数学教材八年级下册第58页习题2）如图4，在正方形ABCD中，点E、G分别在BC、AB上，△ABE经过旋转后得到△ADF.

（1）旋转中心是哪一点？

（2）旋转角为多少度？

（3）在图中画出点G的对应点G′.

原题2：（苏科版初中数学教材九年级上册第19页练习）已知：如图5，在正方形ABCD中，E是BC的中点，点F在CD上，∠FAE=∠BAE.求证：AF=BC+FC.

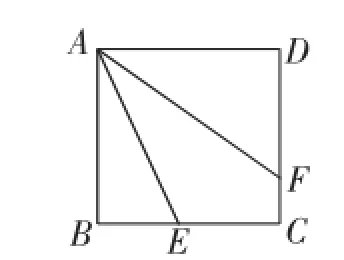
图5

图6

（2）新题赏玩.

如图6，在正方形ABCD中，E是CD边上一点，G是CB的延长线上一点，且AE=AG.

（1）求证：DE=BG.

（2）若点F在BC边上，且∠EAF=45°，连接EF，求证：EF=BF+DE.

（3）如图7，将正方形ABCD放置在平面直角坐标系xOy中，使顶点A与坐标原点重合，点B、C落在第三象限，直线y=x交BC于点F，CD交y轴于点E.若BF=4，EF=10：

①求正方形ABCD的边长.

②在直线y=x上是否存在一点M，使得△OME是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由.

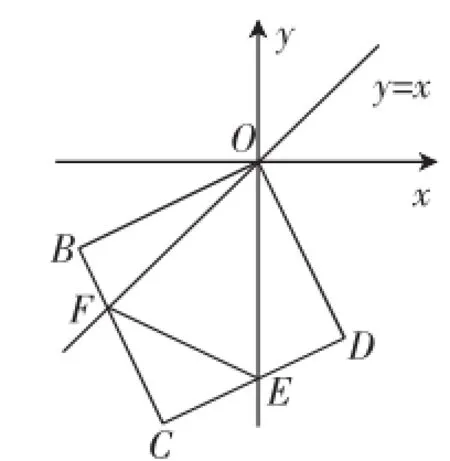
图7

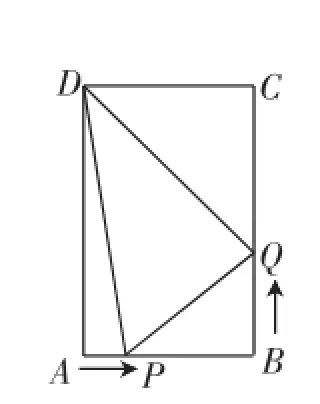
图8

（3）变题意图.

改编题第（1）、（2）小题遵循原题中的知识和方法，考查学生对正方形性质和直角三角形、一般三角形全等判定的掌握情况及旋转变换的思想；为了增加题目的探究性，在第（2）小题结论的基础上，第（3）小题增加了求正方形ABCD的边长，考查勾股定理及一元二次方程等知识，第（3）小题的第②题，又将整个图形放置在直角坐标系中，结合一次函数和图形的相似考查学生对知识的迁移能力和解决问题的能力，渗透了转化、分类、方程（模型）等思想.本题设置的三个问题层次分明，步步深入，兼顾基础和能力，让学生既不能轻易“得手”，又不觉得无计可施.使不同水平的考生在拾阶而上的过程中，思维和能力得到充分释放.

3.变形3.

（1）原题回放.

（苏科版教材九年级上册第97页的思考与探索题）如图8，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，问：几秒时ΔPBQ的面积等于8cm2？

（2）新题赏玩.

如图8，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动（不包括起点和终点），设运动的时间为x，△DPQ的面积为y.

（1）经过多长时间DQ⊥PQ？

（2）在运动的过程中，△DPQ能否成为等腰三角形？若能，请求出运动时间x的值；若不能，请说明理由.

（3）①试求出y与x之间的函数关系式，并说明是否存在x，使得y的值等于10.若存在，求出x的值；若不存在，请说明理由.

②若点P到达B点后继续沿边BC向终点C移动，点Q到达C点后继续沿边CD、DA向终点A移动，当一点到达终点时，另一点也随之停止运动，问：在继续运动的过程中，y的值能否等于10？若能，请求出x的值；若不能，请说明理由.

（3）变题意图.

原题考查的知识点单一，方法简单.为了扩大试题的开放性和综合度，本题以矩形为载体，以点的运动为主线，在课本习题的基础上进行拓展、延伸.第（1）小题设置了经过多长时间DQ⊥PQ，此问可以借助相似或勾股定理列方程加以解决；第（2）小题增加了△DPQ能否成为等腰三角形的探究，可考虑分三种不同情况列方程加以解决，其中不符合条件的解还必须舍去；第（3）小题增加了对△DPQ的面积能否等于10的探究，同时还扩大了点运动的范围，增加了点P在BC边上运动、点Q在CD或DA边上运动两种情形.改编题注重对基础知识、基本能力的考查和数形结合、转化、分类等数学思想的渗透，考查运用方程、函数（模型）思想分析、解决问题的能力.

三、变形感悟

1.要善于借“题”发挥，以“变”促学.

课本是知识的根本，是经典的结晶，也是问题的源泉.课本提供的例、习题作为教材的有机组成部分，是教学中不可忽视的重要内容，它对帮助学生理解基础知识、形成基本技能、完善认知结构、培养和提高思维能力等各方面都起着重要的作用.因此，如何深入挖掘课本典型题目的潜在价值，以求举一反三、融会贯通，为学生的思维发展架梯搭桥，是我们在教学中值得重视和探讨的问题.日常教学中，我们要注重加强对课本习题的研究，对于一些好的题源，教者要能“明察秋毫”，洞察教材的编排意图，在此基础上借“题”发挥，以“变”促学，创造机会，让学生经历从解题到编题，再到解题的全过程，更大限度地发挥习题的应有教学价值.

2.要善于“让学引思”，培养和发展学生的问题意识.

爱因斯坦曾经说过：“提出一个问题比解决一个问题更重要.”在原题的基础上设计和改编新的问题是一项很有意义的数学实践活动.在设计问题过程中，要善于“让学引思”，给学生足够的思考时间和互动空间，使学生的思维得以发展，能力得到提升.在教师的组织和引导下，随着学生身份从答题者到编题者、变题者的悄然变化，学生的主体地位得到充分发挥，问题意识和解题的经验和能力得到提升，最终效果体现在学生学习上的事半功倍.在数学教学中如何培养学生提出问题的能力呢？解决这个问题，首先要采用多种手段让学生对数学学习感兴趣，要善于构建以“问题设计”为中心的学习模式，引导学生由好奇到好问，逐步渗透问题意识，进而上升到勤思善问，追求问题的质量，再到提出有价值的问题.

3.要善于释放话语权，努力让变式教学成为常态.

传统习题课的教学是由教师提出问题学生进行解答或由教师安排学生解答教科书中提出的现成的问题，这种模式的弊端是学生的学习是消极被动的，课堂的话语权和主宰权在于教师，学生的学习缺乏动力和活力.变式教学提倡以课本探索题为源头，在学生力所能及的知识储备范围内，让学生充分参与课本习题的变式与拓展，经历师生交流、生生合作的思维碰撞和智慧生成.教学中，教者要尊重每一位学生的思维，让不同层次的学生都能学有所获.值得我们思考的是，除了对题目所提问题进行变式，我们还可以在解题方法、结论探索、题组学习等方面做一些类似的变式教学的尝试，使学生的灵感得以激发，个性得以张扬，不断提升学生思维的灵活性和创造力，为学生的终身发展奠定基础.

1.章建跃.发展数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

2.罗增儒.试题编拟的技术性建议［J］.中学数学教学参考（中），2008（3）.

3.夏盛亮.引导回归教材，倡导开放教学——一次县级期末卷的命题取向分析［J］.中学数学（下），2014（1）.