例谈巧用均值不等式的基本策略

王志友 (邮编：313301)徐彦辉 (邮编：325035)

浙江省安吉县孝丰高级中学 浙江省温州大学数信学院

例谈巧用均值不等式的基本策略

王志友 (邮编：313301)徐彦辉 (邮编：325035)

浙江省安吉县孝丰高级中学 浙江省温州大学数信学院

均值不等式是最重要而基本的不等式之一,应用极其广泛,巧妙地运用均值不等式常能使许多问题得到漂亮的解决,产生意想不到的效果.均值不等式也是历年来高考和数学竞赛中必不可少的内容.在运用均值不等式时需注意同时满足以下三个条件:(1)各项均为正数;(2)和或积为定值;(3)具有等号成立的条件.但要灵活运用均值不等式，有时还需要熟练掌握一些“诀窍”和“技巧”.宋廷福(2004)提出四条均值不等式的常见变形技巧,即:(1)“拆项”变形;(2)“平方”变形;(3)“条件”变形;(4)“倒数”变形.[1]候有岐(2007)提出六条均值不等式解题的变形技巧,即:(1)拆项;(2)拆幂;(3)升幂;(4)整体代换;(5)平衡系数;(6)分离取倒数.[2]笔者最近整理了灵活运用均值不等式的四条基本策略,即:(1)注意凑配恰当的系数;(2)注意组合搭配不同的项数;(3)注意灵活变形后再运用;(4)注意灵活运用一些基本模型和变式.以下分别举例说明在实际问题中如何把握好这四条基本策略以达到灵活运用均值不等式解题.

1 注意凑配恰当的系数

在运用均值不等式解题时,我们常常会遇到题中某些式子不便于套用公式,或者不便于利用题设条件.此时,均值不等式等号成立的条件具有潜在的运用功能.以均值不等式的取等条件为出发点,通过凑配恰当的系数,常常能将问题得到有效的解决．

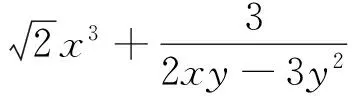
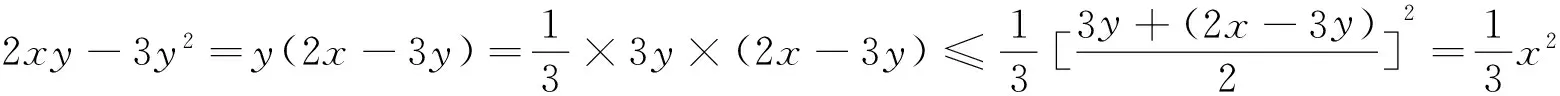
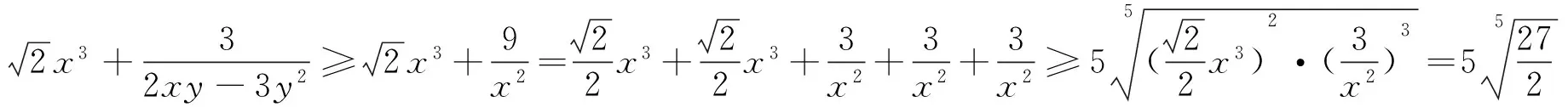
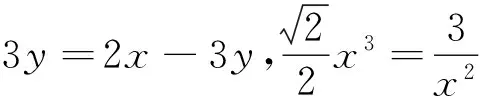
例2 设x3+y3=2,x,y∈R+,求x2+y2+5xy的最大值.

解 由3×1×x×x≤1+x3+x3,3×1×y×y≤1+y3+y3,3×1×x×y≤1+x3+y3, 得x2+y2+5xy≤

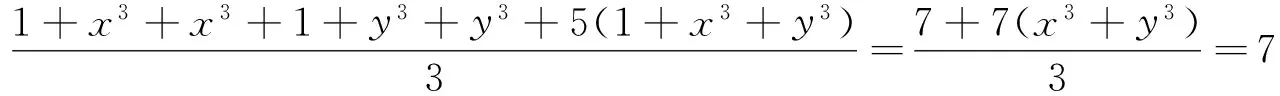
当且仅当x=y=1时取等号.即x2+y2+5xy的最大值为7.

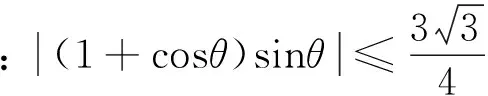
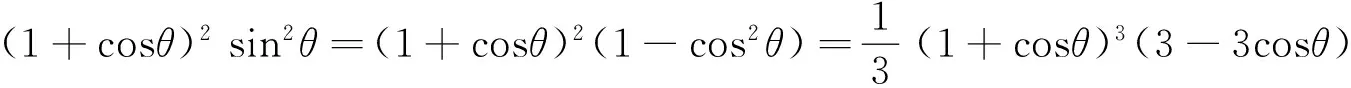
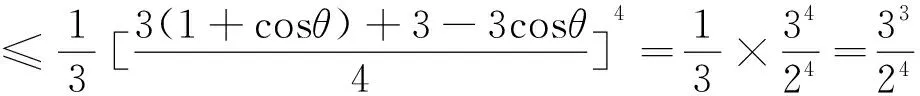
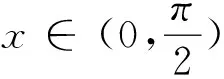
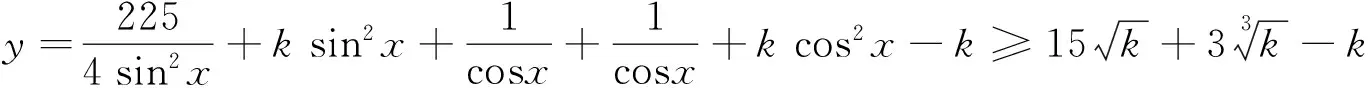
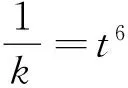
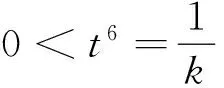
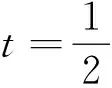
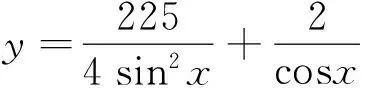
2 注意组合搭配不同的项数

合理拆分项或配凑因式是运用均值不等式的常用技巧,而拆与凑的目标在于使等号成立,且每项为正值,必要时需出现积为定值或和为定值．

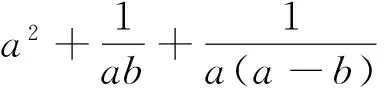
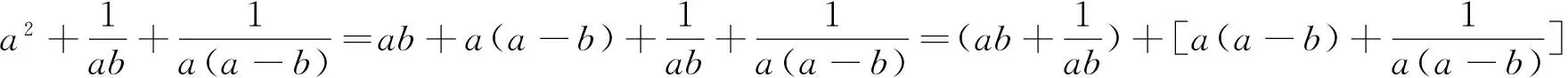
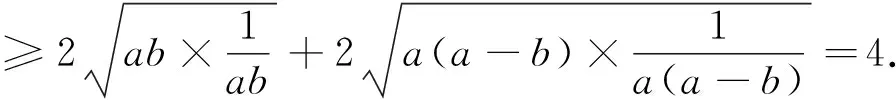
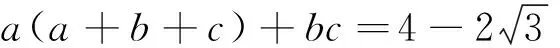
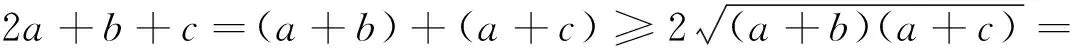
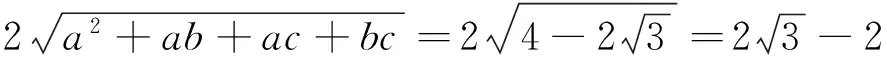
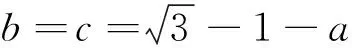
例7 设x、y、z∈R+,且满足xyz(x+y+z)=3k2,求证:

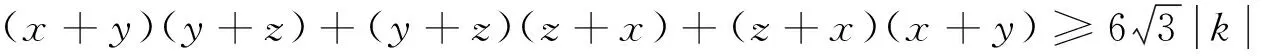
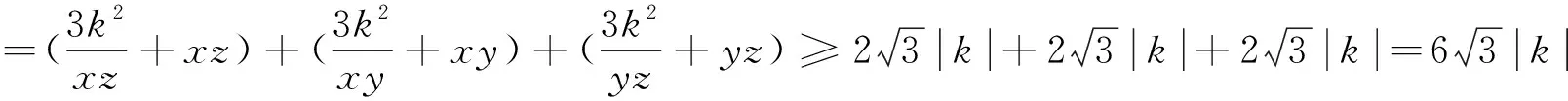
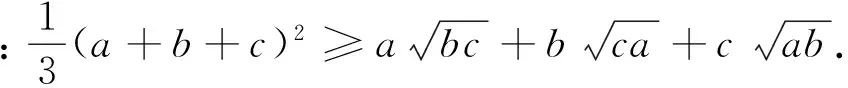
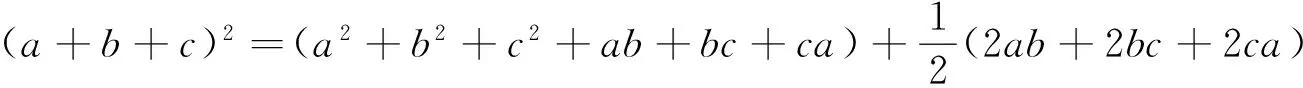
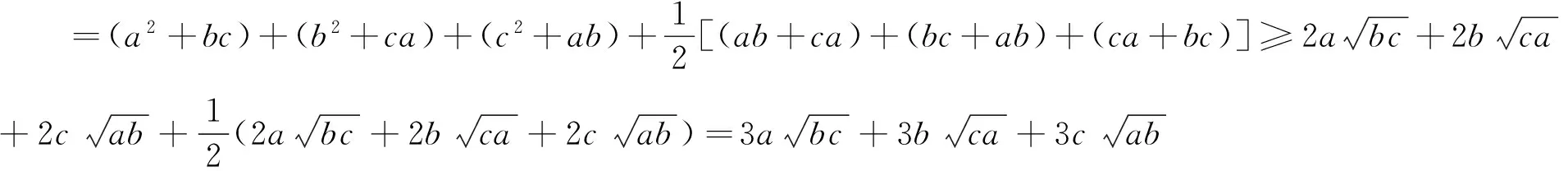
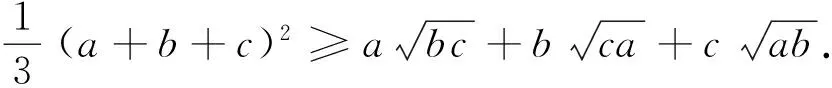
3 注意灵活变形后再运用

运用均值不等式常常要注意灵活变形,多次利用基本不等式时更要注意每次等号是否都成立,同时也要注意基本不等式的变形形式的灵活应用.

例9 设a、b、c∈R+,满足a+b+c=abc,求a7(bc-1)+b7(ac-1)+c7(ab-1)的最小值.

解 由a、b、c>0,a+b+c=abc,得a(bc-1)=b+c,b(ac-1)=a+c,c(ab-1)=a+b.

从而a7(bc-1)+b7(ac-1)+c7(ab-1)=a6(b+c)+b6(a+c)+c6(a+b)

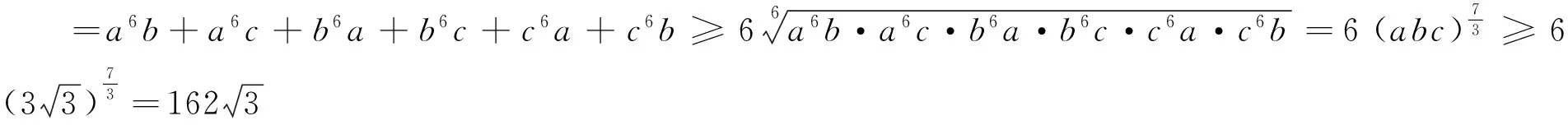
例10 设a、b、c∈R+,求证:(a2+ab+b2)(b2+bc+c2)(c2+ca+a2)≥(ab+bc+ca)3.

证明 设k=

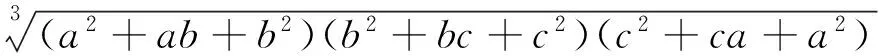
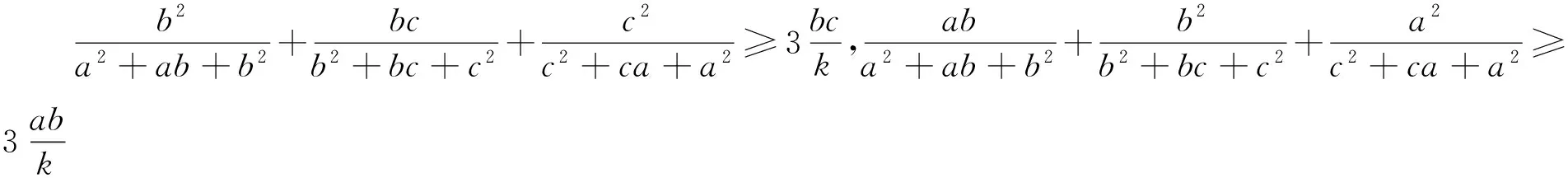
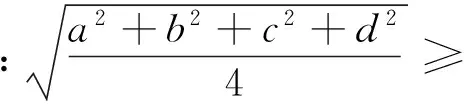
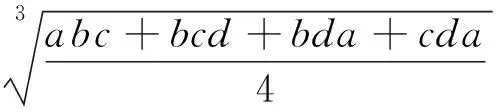
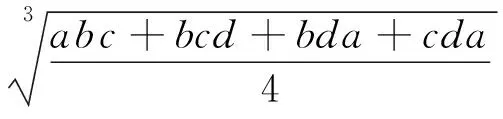
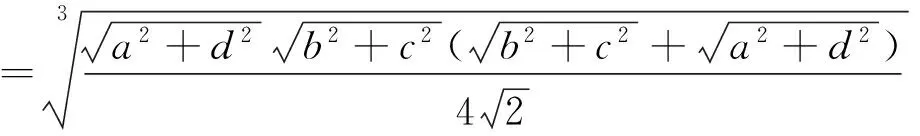
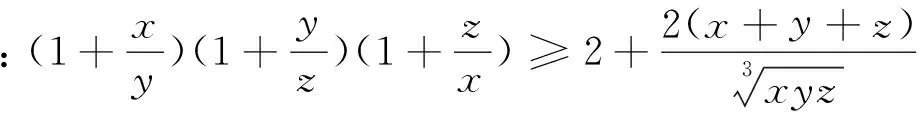
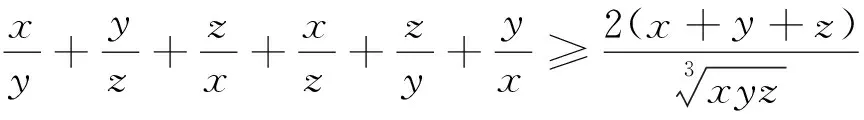
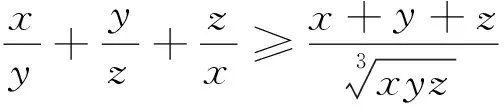
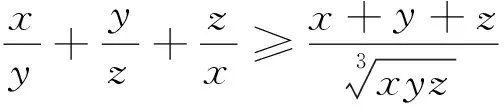
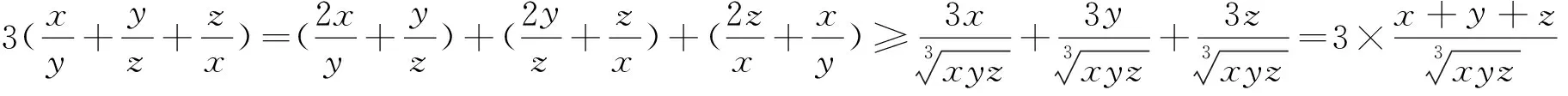
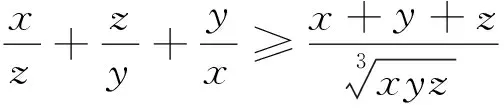
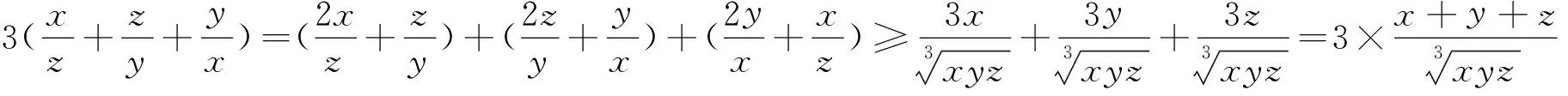
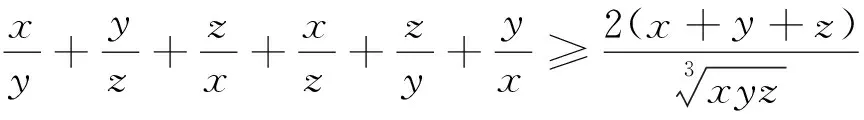
例13 已知xi≥0(i=1,2,…,n),且x1+x2+…+xn=1,n∈N,n≥2,求证:

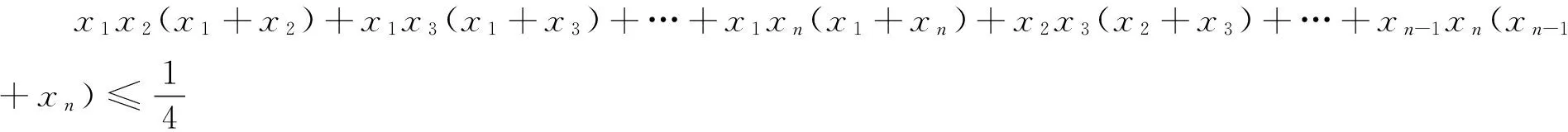
证明 要证原不等式成立,即只要证

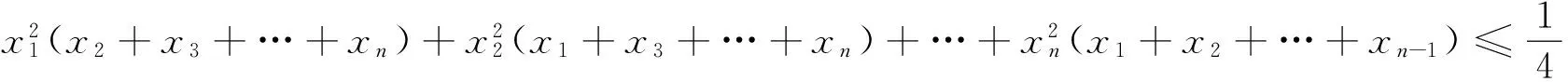
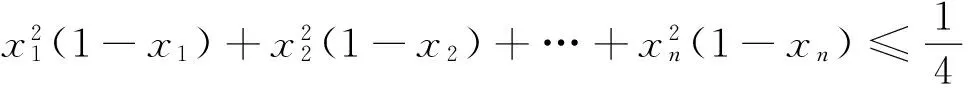
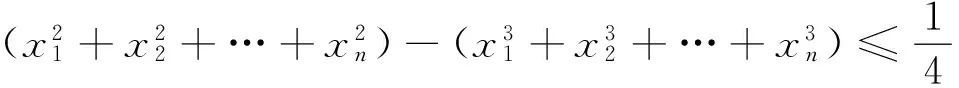
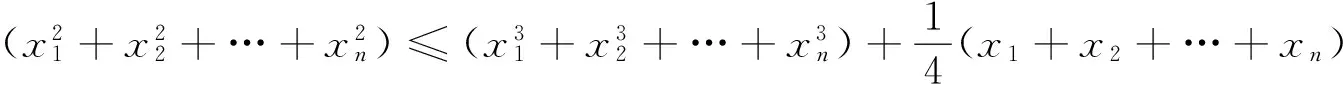
4 注意灵活运用一些基本模型和变式

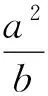
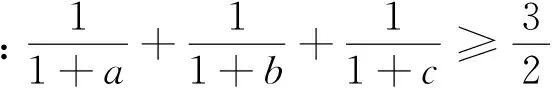
以上三式相加即得证.

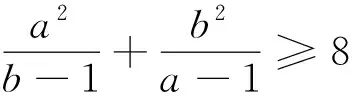
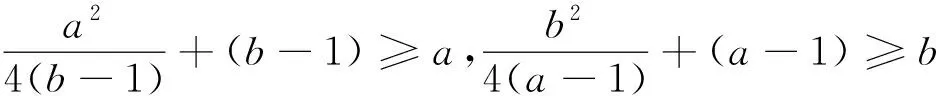
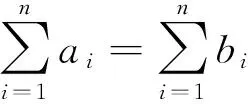
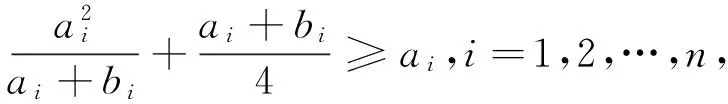
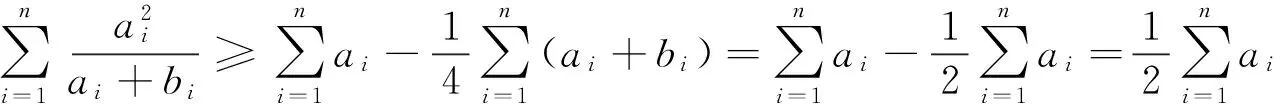
从以上四种基本策略中,我们可以看出:灵活运用均值不等式的关键在于能看出数学问题的本质,进行“拼”、“凑”、“拆”、“合”和“放缩”等变形技巧,以构造出均值不等式的条件结构.当然,要熟练掌握这些策略和技巧,一方面需要加强学习和训练,以积累经验;同时,还需要真正提高数学素养,提高对数式符号的观察能力、直觉洞察力和数学的美感,以及对数式符号结构规律把握的敏感性和变形能力.没有这两条,要真正灵活运用均值不等式几乎是不可能的.

1 宋廷福.例说均值不等式的变形技巧[J].中学生数学,2004(8，上):11

2 候有岐.运用均值不等式解题的变形技巧[J].中学数学杂志,2007(1):40-41

2017-01-16)