关于一道最值问题的多元思考

方王思喆 (邮编：235000)

安徽省淮北市第一中学

关于一道最值问题的多元思考

方王思喆 (邮编：235000)

安徽省淮北市第一中学

方程，既是中学数学的知识主线，也是高考的必考内容之一，其考查角度和形式灵活多变，涉及的知识、能力和数学思想方法多样，能够全面衡量考生的数学素养.对于考生而言，如何将方程与最值问题关联，并从复杂的题目线索中找出恰当的解题思路并非易事.以下笔者将以2011年高考浙江试题的填空题第16题为例，分析不同的解法的思路和考查目标，希望能给大家一定的启示.

(2011年浙江高考试题)已知x、y∈R，4x2+y2+xy=1，则2x+y的最大值为______.

解法1

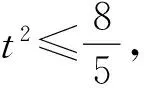
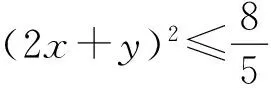
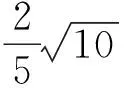
解法分析 该解法的关键在于把2x+y看成一个整体t，在方程判别式△≥0这一条件下，将判别式(3t)2-4×6×(t2-1)看成一个关于t的一元二次方程，再由△≥0这一条件求出t的范围，从而确定2x+y的最大值.这是典型的变量替换法，要求考生充分观察题目形式特点，运用整体性思维将复杂问题简单化.

解法2

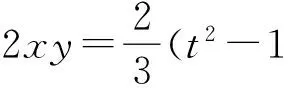
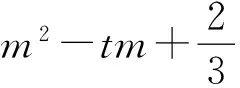
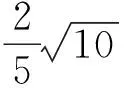
解法分析 该解法需要我们熟练应用根与系数的关系，构造恰当的方程，再由判别式来求得t的范围.此解法的关键是把2x和y看成某方程的两根，巧妙地逆向使用根与系数关系，进而将所求问题转化，以达到更好解答的目的.

解法3

在上式4x2+y2+xy=1中，

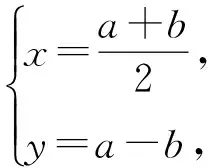
则原题等价于：已知5a2+3b2=2，求2a的最大值.

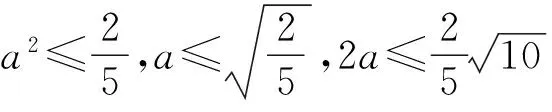
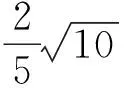
解法分析 该解法的关键是通过将x和y进行恰当的变量替换，以消去其乘积项，将4x2+y2+xy=1转化成5a2+3b2=2，再利用平方数的非负性来求解.这需要具备一定的构造能力和逆向思维能力，以达到化繁为简的目的，对某些同学来说有一定的难度.因此，在平时的数学学习过程中，要注意将各类零碎的数学知识串成一条线，形成知识间的关联结构.

解法4

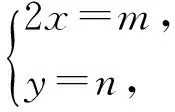
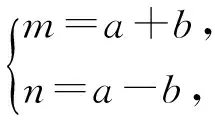
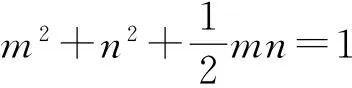
则原题等价于：已知5a2+3b2=2，求2a的最大值.以下解答步骤和解法三是相同的.

解法分析 解法三和解法四属于同一类型，前者的思维跳跃程度更大，后者通过中间变量的过渡，更易于理解.这说明类似的解法也有不同的切入点，考生可以根据自我的思维状态水平选择恰当的方式，同时也说明数学思维过程的重要性.

解法5

对原方程式进行变形，令4x2+y2+xy=m(2x+y)2+n(x-ty)2=1，t>0.

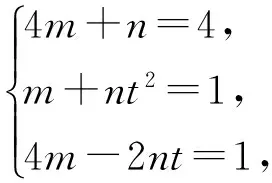
因为m(2x+y)2+n(x-ty)2=1，

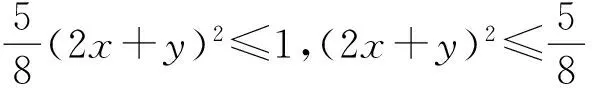
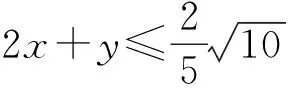
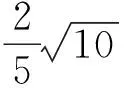
解法分析 这种解法注意到原式4x2+y2+xy只包含了三个二次项，故将其配方成2x+y和x-ty的平方数形式，利用多项式相等原则，由对应系数相等得出关于m、n和t的方程组，进而由平方数的非负性求得2x+y的最大值.此解法的难点在于等式中巧妙地假设了m和n以及t，利用待定系数求得最值.

解法6

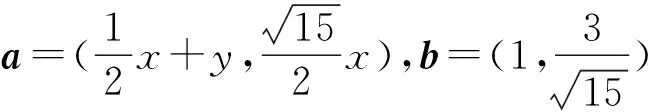
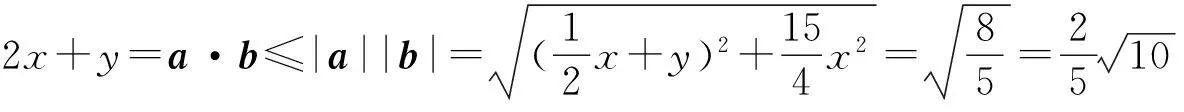
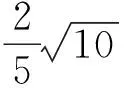
解法7

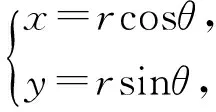
那么(2x+y)2

=r2(4cos2θ+sin2θ+cosθsinθ)

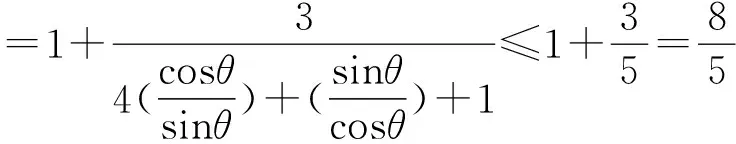
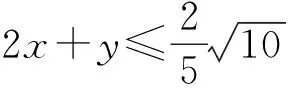
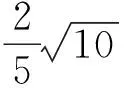
解法分析 该解法由参数方程入手，没有直接求解2x+y，而是将(2x+y)2化简成易于求解的三角函数形式，通过均值不等式求得(2x+y)2的最大值.这种解法很大程度上检验了我们对数学知识的综合把握，体现了数学方法的整合性.

以上列出的七种方法只是个人认为比较具有代表性的解题方法，还有更多的巧妙方法等待同学们去发现.无论如何，在求解类似的最值问题时，请尽可能地发散自己的思维，找到数学知识与特定解题方法的连接点，学会融会贯通和方法整合.

2016-12-16)