关于“分式”一章教学的几点思考

刘华为 (邮编：200435)

上海市岭南中学

关于“分式”一章教学的几点思考

刘华为 (邮编：200435)

上海市岭南中学

分式既是学生在学习整式基础上对有理式认识的一次完善与拓展，也是从结构特征上对由数(分数)到式(分式)认识的一次迁移与升华，因而“分式”一章教学应当基于两点：一是以类比分数为切入点，完成分式相关概念与性质的学习，培养学生对新知学习的迁移能力；二是以转化思想为抓手，确立分式问题整式化处理的基本策略，培养学生解决问题化归能力．本文试图从上述两点出发，并结合平时的学习体会与教学实践，谈谈对“分式”一章教学的一些不成熟思考，以求抛砖引玉，更愿得到广大同仁斧正．

1 以实际问题引入分式到底可以走多远？

在学习分式概念时，常常要对一些有理式进行观察分析，找出整式与分式的区别，归纳出分式的基本特征，从而“生成”分式概念．特别在各类公开课、评比课和杂志刊登的教学设计中，执教者往往喜欢通过解决实际问题而获得这些有理式，以突出“数学来源于生活又服务于生活”的新课程理念，并激发学生学习兴趣和强化应用能力．这本无可厚非，但由此引发的在数量和难度上的泛滥而导致喧宾夺主甚至本末倒置的现象却应当引起大家关注．

案例1 在一节“分式的意义”的区级公开课上，新课伊始执教者出示了七道应用题(2 道行程问题、2道工程问题、1道浓度问题、1道数字问题和1道营销问题，几乎涵盖了应用题的所有类型)，花了近17分钟的时间列出了10个方程(有3道题学生各列出了2个方程)，并从中抽取了16个有理式(8个整式和8个分式)，只给学生不足1 分钟的时间进行观察，便在教师“分母有什么不同”和“分子与分母有什么特征”的直接“启发”下，师生共同归纳出分式的概念．本环节花了近20分钟的时间，但留给需重点突出的“观察、分析、类比(分数)和归纳”概念形成的时间还不足3分钟，应用题的过量设置是否有喧宾夺主之感？

案例2 某外省市一位特级教师来本区上了一节“分式的意义”的示范课，也是以实际问题引入，第一道行程问题处理较为顺手，但在处理第二道应用题时耗时近8分钟，效果却仍不尽如人意．

题目 甲、乙两人两次同在同一个超市购买水果(假设两次购买水果的单价不同)，甲每次购买水果a千克，乙每次购买水果用了a元．若规定谁两次购买水果的平均单价低，谁的购买方式就合算，请问甲、乙两人购买水果的方式中，哪一种更合算？为什么？

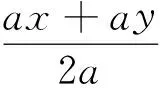
教学建议 一方面，通过实际问题引入新课的主要意义在于突出“数学生活化”的新课程理念，着重在于“引”而非在于“培”(培养应用能力)，更何况分式的来源也不仅局限于生活问题，整式的除法运算也是生成分式的重要来源之一；另一方面，分式概念教学的重点是引导学生通过对一组有理式的观察，分析出“整式与分式的区别(分式中分母含有字母)”和“分式的基本特征(分子分母均为整式且分母中)”，并类比分数定义归纳出分式概念．因此作为引入的实际问题选取不宜贪多也更不必求难，可从学生熟悉的问题展开(如一列动车从A地开往相距400千米的B地需t小时，则它的平均速度为______)，再作适当的变式探究(若动车继续往前开往距B地a千米的C地还需20分钟，则这列动车从A到C的平均速度为______)，使列相关有理式为信手拈来之举，把时间更多地留给“观察、分析、类比与归纳”，再现“分式”概念的形成过程，从而既突出了重点又不人为增加难点，这才是科学的处理策略．

2 放弃类比失去了什么

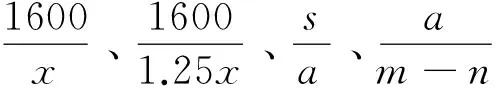
显然，案例中对归纳分式概念的处理方式值得商榷，错失了一次对学生迁移能力培养的大好时机．也许执教者觉得直接让学生用语言表述分式概念可能有一定的难度，所以采用了先让学生划线并朗读教材上分式概念，再通过例题辨析加深理解的常规处理策略．事实上，若巧妙地类比分数定义，实现由数到式的迁移，学生归纳出分式概念也不是很棘手，即便不严密，但教师可通过反例引导学生反思并逐步完善．

教学建议 在学生归纳定义语言组织受阻时，可通过下列问题驱动：

问题2 分式与分数的不同点在哪里？(突出数与式的区别与联系)

由于种植户分散不利于统一管理及产业化，规模化经营。因此，怀远县政府应该提供资金支持，对怀远县的土地和住户进行统一规划管理。在地势平坦或者种植地较多的地区将住户区集中起来，建立社区。剩余土地集中规划为种植用地，建设石榴产业示范区。并通过对土质、地形等一系列情况的勘测，在不同的区域种植不同品种的石榴。分区域将土地承包给农户种植。进行规模化，集约化生产。而在农户较为分散，种植区不集中的地区对农户进行技术指导，通过科技创新，研究出新的品种，以独一无二的特色品种吸引消费者的眼球。并且可以直接联系加工企业收购当地石榴，降低销售成本。

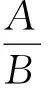
如此处理的优越性在于：不仅加强了对学生归纳整理和语言组织能力的培养，加深了对分式概念的理解，而且还注重了学习方式的转变，突出了学法指导，促成了迁移能力的有效形成与发展，为学生处理问题又打开了一扇思维之门．另外，关于分式性质与运算等知识的学习，也可通过类比分数而获得以最大限度地提高课堂效率，教学中也要予以足够的关注．

应当指出的是，一方面，类比迁移是处理问题一种非常重要的思维方式，是解决问题一种行之有效的常见手段，是形成发展性学习力的必备一环；另一方面，无论是形式上的“由数到式”“由低维到高维”“由单元到多元”等类比，还是本质上的“知识迁移”“方法迁移”和“思想迁移”等类比，在初中数学学习中无处不在，无时不有．因此，如何以此为契机重视类比教学，有效地促进学生思维的正向迁移，逐步掌握类比推理的思维方法，形成探索新知和处理问题的迁移能力，是一个值得广大同仁深入思考和不断探究的课题．

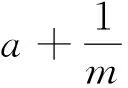
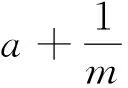
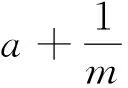
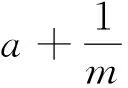
4 解分式方程的着力点在哪儿

文[3]提到一个关于分式方程的教学案例，执教者由实际问题引入分式方程得出定义后，便直接讲授解分式方程的具体步骤，并归纳出“一找二去三解四验”的八字口诀，最后通过大量的例(习)题操练巩固．

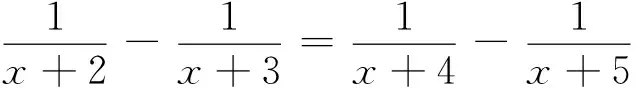
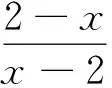
至此(无论出现哪一种结果)，总通过问题驱动引导学生思考上述变形过程的本质就是化分式方程为整式方程(即方程两边同乘以x-2去分母)；然后再引导学生依据等式的基本性质，剖析变形过程的科学性，归纳出解分式方程的基本操作流程．

若学生直接去分母求解，就通过追问“你是怎么想到的”和“依据又是什么”引导他们反思剖析，学会思考，渗透转化思想、掌握化归方法．

如此处理的优越性还在于，不仅突出了过程教学，强化了学生对解分式方程由“怎样做”到“为什么这样做”的理解深度，掌握了转化思想的精髓，吃透了增根产生的缘由，而且所有问题的解决都是由学生通过自主探究而得，即在获得知识的同时，注重了思想的渗透、方法的形成和能力的自我构建，真正落实了“以学生发展为本”的新课程理念也！

1 汪宗兴.基于“分式”课例浅谈初中数学概念教学[J].中学数学：下旬，2016(7)：30-34

2 刘东升.一次期中考试阅卷随笔[J].中学数学教学参考：中旬，2016(1-2)：109-110

3 王纯旭. 大家都记住了吗？[J].中学数学教学参考：中旬，2013(12)：22-24

2017-02-14)