源于教材 高于教材——一道教材习题的改编之“旅”

蔡勇全 (邮编：641300)

四川省资阳市外国语实验学校

源于教材 高于教材
——一道教材习题的改编之“旅”

蔡勇全 (邮编：641300)

四川省资阳市外国语实验学校

纵观近年来的高考数学试题，许多题目“取材于教材，但又不拘泥于教材”，教材中例、习题的身上往往能找到它们的“基因”，它们是对教材原题的变形、改编与综合.我们知道，教材中的例、习题是编者精心构思的典型题目，也是重要结论、命题、定理或数学思想的载体，它们的延伸、转化和拓展呈现了丰富的数学知识，因而教材是编拟各类试题的源泉.对教材原题的变式、挖掘、探究，既能抓住数学本质，加深数学理解，又能提高解题能力，促成思维的广阔性、深刻性和灵活性.本文以一道教材习题为例，力求体现改编探究的思维过程，供大家参考.

题目 设实数x和y满足

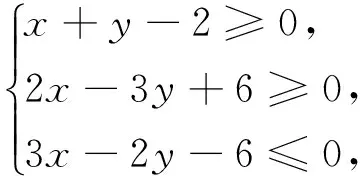
上述题目是人教A版必修5第91页练习1中的第(2)题，属于线性规划范畴.线性规划是近几年来新课标教材增添的内容，其内容本身就已经颇具新颖性，而且线性规划问题具有知识交融、解答灵活、应用较广等特点，各种数学思想方法也能较好地体现在其解答过程中，因而在历年高考中常考不衰，久考仍新，以其为载体、与其它知识综合融汇的题目无一不体现了一定的创新性.

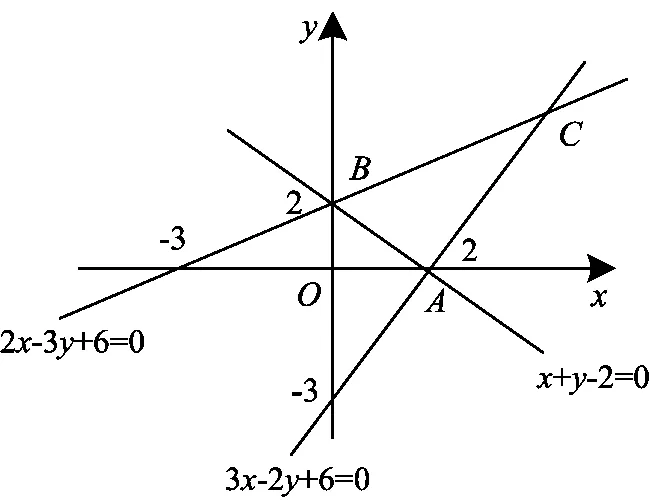
为顺利说明后续的编拟过程，有必要先简解此题，根据约束条件，作出的可行域为下图中的三角形ABC内部区域(含边界):

下面从改编成题的渠道以及对设置问题的方式进行创新的办法来编拟相关的题目:

我们知道，最大(小)值的相反数即为最小(大)值，于是可以得到改编1:

改编1 设实数x和y满足

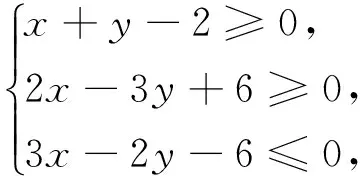
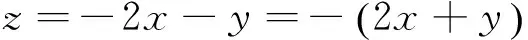
改编2 设实数x和y满足

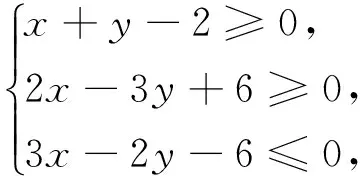
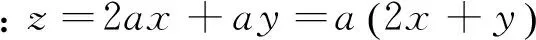
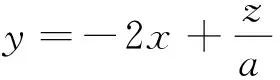
在改编2的基础上，再进一步思考，如果从形式方面下设置问题的方式进行创新，即把问题的条件与结论交换位置，使之成为逆向条件探索性问题，题目又将呈现怎样的变化呢？于是可以得到改编3:

改编3 设实数x和y满足

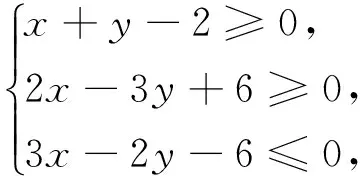
有了上述改编2的简解作为基础，改编3是容易突破的，只可能是a>0,18a=54,则a=3.当然，改编3仍较好地检测了分类与整合的数学思想.改编2的简解实际上告诉我们，目标函数的最大值与最小值均与实数a的符号相同.

如果对条件中的最值“动手术”，还可产生如下逆向条件探索创新型题目:

改编4 设实数x和y满足

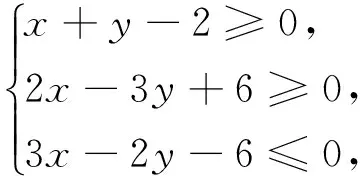
改编5 设实数x和y满足

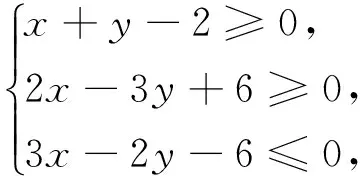
改编6 设实数x和y满足

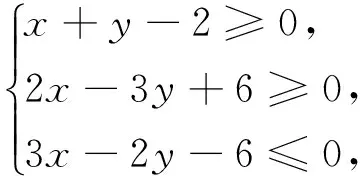
改编3、4、5、6的最值均不为0,说明a≠0.另外，改编3、4、5、6的局限性在于等式右边的参数仅有a,如果x与y前面的参数不相同，那么题目也不可能再要求把两个参数同时求出，势必改变探索目标，于是得到改编7:

改编7 设实数x和y满足

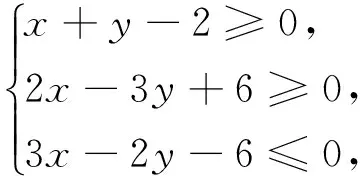
一方面，对于改编7,我们需要思考，目标代数式是否还有其它类型，答案是肯定的，诸如:

改编8 设实数x和y满足

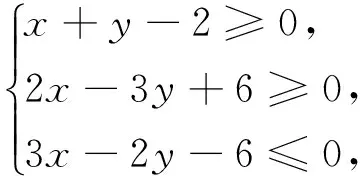
改编9 设实数x和y满足

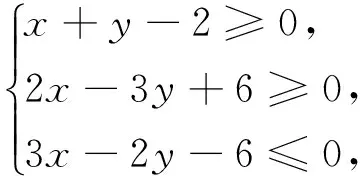
同样针对改编7,若a、b同为负数，则题目中最值的表述一定会完全相反，因此又可得到改编10:

改编10 设实数x和y满足

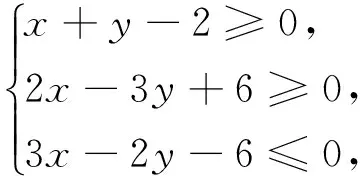
类似由改编7向改编8、9的过渡，对于改编10,一方面，改变目标代数式，可以得到:

改编11 设实数x和y满足

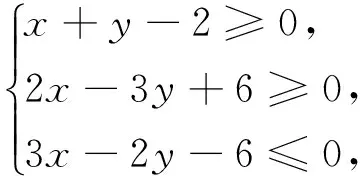
改编12 设实数x和y满足

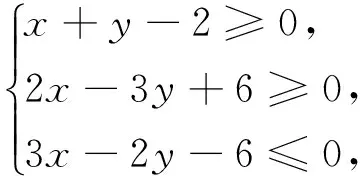
改编7、9、10、12突出体现了线性规划与基本不等式知识的交汇性.另外，受改编2、3、4、5、6的启发，我们不免想到，如果最初的目标函数不是线性的，而是其他类型，但同样要设计成逆向条件探索性问题，又当如何呢？于是可以进一步得到改编13这一创新型题目:

改编13 设实数x和y满足

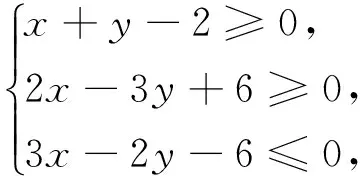
另外，在改编13的基础上进一步思考:既然最值问题往往与不等式恒成立问题挂钩，那何不把不等式恒成立问题融入改编13中，这样一来，借助不等式恒成立问题的特点，既可以有效检测思维的逻辑性，也可由于不等式恒成立问题解法的灵活与多样，检测思维的创造性，因此顺理成章就产生了改编14:

改编14 设实数x和y满足

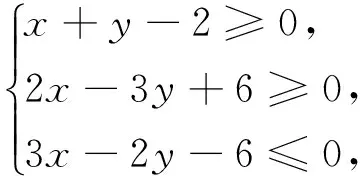
改编14的创新之处体现于线性规划与不等式恒成立问题的交汇，综合检测线性规划、不等式变形、最值、不等式恒成立、分类整合数学思想等知识，难度较大.另外，根据可行域可知，改编14中恒成立不等式的分母2x+4恒为正，因此去分母后进一步得到难度稍大的改编15:

改编15 设实数x和y满足

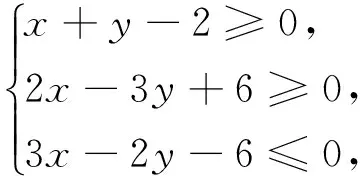
改编14与改编15皆属于线性规划与不等式恒成立问题的交汇性创新题，从中可以看到，创新型题目的命制仍然不要忘记贯彻“对支撑学科知识体系的主干知识要重点考查”这一核心理念.

接下来，我们应该思考，本案例的改编还有哪些视角呢？改编过程还可以持续下去吗？比如，同样是线性规划与不等式恒成立结合的创新型问题，能否就约束条件进行改编呢？于是，经过一番斟酌思考，得到改编16:

改编16 设实数x和y满足

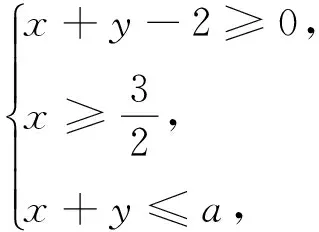
存在与任意犹如一对“孪生兄弟”，它们往往聚在一起为大家所研究.因此，能否把改编16这一“恒成立”问题演变为“能成立”问题呢？答案是肯定的，比如下面的改编17:

事实上，改编17的本质是求当直线2x-y=6经过可行域时实数λ的取值范围，进一步思考，同一样是“能成立”问题，题目中的“能成立”等式能否改为“能成立”不等式呢？于是得到:

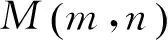
对比改编21与改编16,虽然同属不等式恒成立问题，但绝妙之处在于:改编16把参数放在了约束条件中，而改编21把参数放在了恒成立不等式中.

回到改编16,进一步思考，既然约束条件改编成了含参形式，那么题目最终的目的一定是探求参数的取值或取值范围，因此还必须给出一定的辅助条件，从而题目自然而然就演变成为了逆向条件探索创新型题目，那么其它应给出的条件还有哪些形式呢？这一点不难想到，比如区域的面积，目标函数的最值等，于是得到如下改编22、23、24、25:

改编22 设实数x和y满足

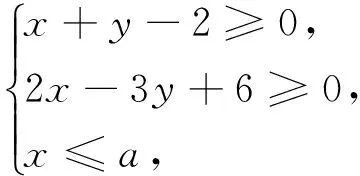
改编23 设实数x和y满足

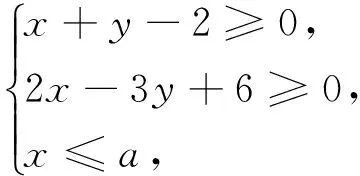
改编24 设实数x和y满足

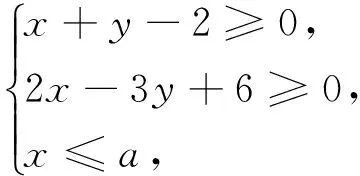
改编25 设实数x和y满足

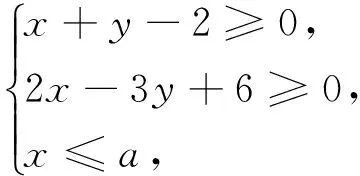
类似于前文改编3、4、5、6那样的逆向条件探索性问题向改编7、8、9、10、11、12这样的给出相关最值条件而另求最值的问题的演进，改编25可进一步改编为:

改编26 设实数x和y满足

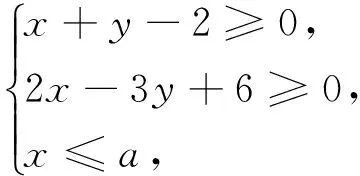
前面的一系列改编注重从条件本质的增删或改换来实现，那么既然改编了这么多，现在不妨回过头来反思，回到原点，回到问题的本来面目，即如果不改初衷，维持教材原型的中心任务，但用其他知识来创新地衬托目标函数，是否可行呢？反复思考，有了下面的改编27:

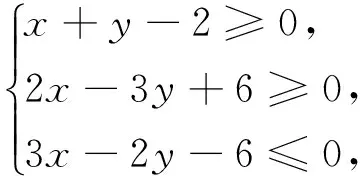
用平面向量的数量积来体现目标函数，新颖别致，但不可否认的是，这种给出目标函数的方式略显直接，事实上，目标函数的给出还可再隐晦一些，比如:

如此设计，学生找到目标函数就成为了解题任务之一，这不正是学科内知识的交汇与综合的绝佳体现吗？既然提到知识的交汇，那么不得不说与线性规划联系紧密的同宗同源的其它解析几何知识，比如两点间的距离，因此可得到如下改编29:

如果题目中的距离隐含化，那么改编29可进一步演变为改编30:

对比改编30与前文改编23,不难发现二者的区别主要体现在两个方面:改编23的约束条件在变化，而且其中含有参数，改编30的约束条件很明确，其中不含参数；改编23属于逆向条件探索创新型题目，即已知目标函数的最值，探求参数的取值，而改编30是在具体约束条件下探求具体目标函数的取值范围.

事实上，无论是平面向量还是两点间的距离，与线性规划的关系并不算遥远，因为几者都有“形”的一面，那么与线性规划的关系遥远的知识内容能否与线性规划交汇呢？显然是可以的，比如把线性规划与概率交汇起来得到改编31:

行文至此，想到前文第3.2.4节“从问题解答方面进行创新”——“(2)妙解型”中曾提到过借用“行列式”、“矩阵”等概念来编制创新型题目的方法，并给出了具体的命题范例，那么，是否可以移植到此处呢？

最后，为了增强题目的可读性、趣味性，让题目更生活化、更接地气，我们能否可以考虑采用现实生活背景来承载线性规划问题呢？这显然是可行的.几经酝酿，以当下轰轰烈烈的“大众创业、万众创新”社会背景来编拟，于是有了改编33,不仅以此结束本案例的编拟，同时也与教材原型遥相呼应.

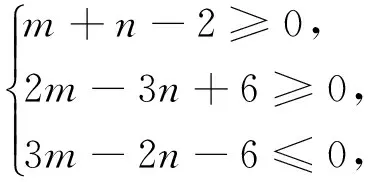
改编33的创新之处不仅体现在线性规划在现实生活中的应用这一外在表象上，而且还体现在不同于以往的惯例上——目标函数需要自己寻找.

创新型改编似乎没有止境，但限于篇幅，本案例的后续改编就不再进行下去，纵观本案例中相关题目的编拟过程，想说的是，我们在编拟数学题目时，首先应选择设计渠道(大方向)，比如此案例就是利用了改编成题渠道，在此大方向下采取了从形式方面创新和从内容方面创新两种策略，而且在改编设计时，如果成题条件较多，那么就应根据立意需要，合理选取题目中的某些条件或结论进行改编.

2017-01-14)