让“研题”走进高三数学课堂教学的尝试与感想
2017-04-24江苏省姜堰第二中学
江苏省姜堰第二中学
朱传美 (邮编:225500)
让“研题”走进高三数学课堂教学的尝试与感想
江苏省姜堰第二中学
朱传美 (邮编:225500)
江苏省兴化市教育局教研室 张 俊 (邮编:225700)
“研题”是数学老师提高数学水平的重要途径.在高三的解题教学中,笔者研究发现:选择合适的题目,让“研题”走进高三数学课堂,对提高高三学生的数学解题能力大有帮助,经多次尝试研讨,形成“选题,审题,解题,变题(或拓题),品题”的课堂教学组织模式,深受学生欢迎.
研题;选题;审题;解题;变题(或拓题);品题
1 问题的由来
《普通高中数学课程标准(实验)》在第四部分(实施建议)中指出:教师应根据不同的内容、目标以及学生的实际情况,给学生留有适当的拓展、延伸的空间和时间,对有关课题作进一步探索、研究.
笔者在针对课题《高中数学课堂教学模式创新与学习方式转变的实验研究》开展课堂教学研究时,进行了一些新的高中数学课堂教学模式的尝试.其中,对在高三数学课堂适当地开展“研题”教学的尝试略有收获.
2 问题的提出
我们知道,“研题”是数学老师提高数学水平的重要途径,笔者就从中受益匪浅.在高三的解题教学中,选择合适的题目,让“研题”走进高三数学课堂,对提高高三学生的数学解题能力大有帮助.经多次研讨,形成如下课堂教学组织模式:整节课完全由主持人来主持完成(主持人在本班同学中选举产生),教师以旁观者的身份进入课堂,适时作为参与者与学生一起活动,适时作为指导者给出建议或提示,适时作为评价者给予评价.具体的“研题”步骤逐步完善为如下五个环节:选题,审题,解题,变题(或拓题),品题.
3 问题的实施
下面是一道模考填空题的课堂“研题”实录.
3.1 选题
主持人:经班级“研题”小组核心成员研究发现:这次泰州三模的填空题第14题具有很高的研讨价值,此题虽是填空题的压轴题,但却是一道入口宽思路广的好题,所以决定对这道填空题进行一次“研题”交流.首先请同学引领我们感受一下这道题,大家欢迎!
3.2 审题
(学生一边讲解,一边投影)

生1:此题主要考查解三角形的基础知识,重点考察数据处理能力.第一思路应该是正弦定理或余弦定理, 这是多数同学的考场解法,但好多同学无法进行到底,还有同学选用了坐标法,当然后来经同学们共同研究,又开发了很多新的解法,下面我们就一起来慢慢欣赏吧!
3.3 解题
主持人:首先有请同学展示一下正、余弦定理的解法
生2:正弦定理或余弦定理应用的难点是在众多三角形中,能否找到不同三角形之间的联系及选择哪个三角形作为解题的突破口.我在分析题目已知条件时,抓住题中的关键字眼:当∠C变化时,得到了解法1.

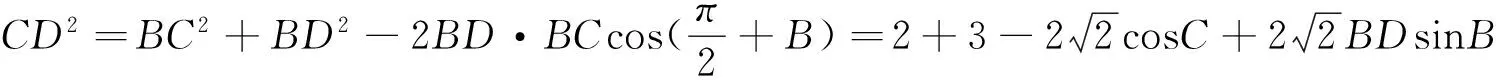
主持人:鼓掌!
掌声……
生3(害羞地):这是我考试时的解法,当时,我可花了好长时间,虽然做对了,但耽误了后面题目的解答.

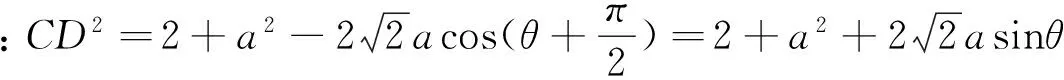

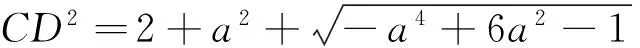


解得:a2=1或a2=5.
经单调性分析 可得:当a2=5时,f(a)max=9,故CDmax=3.
生3 :后来经改进,又得到解法3和解法4,
解法3 经两次换元后得到了快速解决,巧妙地回避了导数.
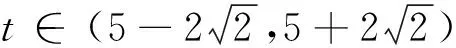

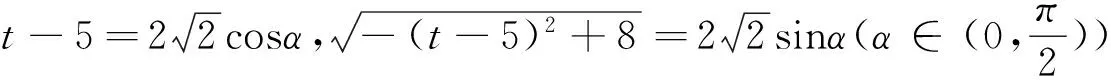
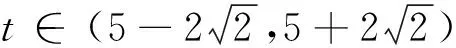

显然,当t-5>0时,CD2才可能取得最大值,所以CD2≤
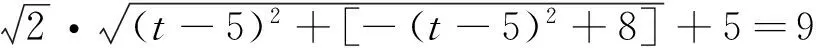
当(t-5)2=4,即a2=5时,等号成立.
众生鼓掌.
生4:坐标法
解法5 建立如图1所示的直角坐标系,

图1
设A(a,0),C(x,y),D(0,-a)

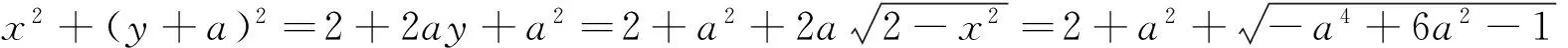
下同解法1
众生:哇!异曲同工,妙啊.

图2
生5:我也用了坐标法,但略有不同.
解法6 建立如图2所示的直角坐标系,
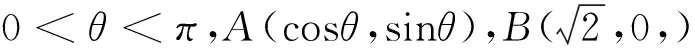
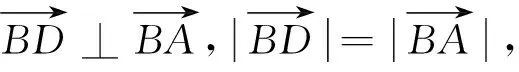



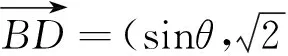

图3
掌声……
生6:初等几何法
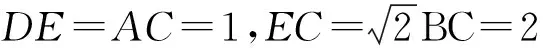
因而CD≤DE+EC=3.
众生(哗然):好简洁!然后是持久不息的掌声.
生7:竞赛知识
解法8 本题可直接由托勒密不等式得到,事实上,这正是本题的背景.
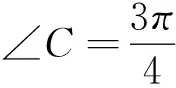
众生(茫然):不懂?
众生:哦.原来如此,真高手啊!
3.4 变题(或拓题)
主持人:通过交流,我们得到了此题的8种解法,真让我们大开眼界,我们班真是藏龙卧虎啊!我听说我们班好多“命题达人”还对此题给出了变题,有请这些命题达人.
生8:△ABC中,已知BC=a,AC=b,以AB为边向△ABC外作等边三角形ABD,问当∠ACB为多少度时,C、D两点间的距离最大?最大值是多少?
生9:对于原问题,在其它条件不变的前提下,以AB为斜边向△ABC外作等腰直角三角形ABD,又会什么样的结论呢?以AB为直角边向△ABC内作等腰直角三角形ABD,又会什么样的结论呢?
生10:以AB为斜边向△ABC外作有一个锐角为30°直角三角形ABD,又会什么样的结论呢?AB为直角边呢?
生11:以AB为边向△ABC外作等边三角形ABD,问当∠ACB为多少度时,C到△ABD的中心O的距离最大?最大值是多少?
生12:对于原问题,在其它条件不变的前提下,以AB为边向△ABC内作等边三角形ABD,使C在△ABD外,不妨设BC=a,AC=b,且b>a,又会有什么结论呢?
……
3.5 品题
主持人:我们从代数和几何这两个基本角度出发得到了这么多的解法,巩固了多种最值问题的处理策略,更大的收获是我们一起学习了托勒密不等式,了解了此题的真正命题背景.可见命题者的“用心良苦”,当然还有同学大胆地给出变题,真让我们在座的每位受益匪浅.
师:经同学们短短两天时间的准备,就能得到如此丰厚的“研题”成果, 说明这是一道很值得我们研究的好题.一题多解、一题多变是“研题”的两个最基本的方向,通过这次“研题”,说明同学们已较好地掌握了这两个基本方法.当然,“研题”的方向还有很多,有待同学们以后逐步掌握.课后,同学们可以好好地研究一下托勒密不等式及托勒密这位伟大的数学家,说不定你们又能找到新的“研题”点.
4 问题的收获
4.1 “一切为了每一位学生的发展”是新课改的最高宗旨和核心理念.在此背景下,新课改的学生观提出:学生是学习的主体,学生具有巨大的发展潜能,每个学生都是独立的、不依教师的意志为转移的客观存在,不可以由教师任意捏塑.由此,新课标对教学工作提出了更高的要求,如何激发学生的潜能,提高学习效果是一个不容忽视的迫切问题.在传统教学模式的支配下,学生往往处于被动接受之中,学生潜能被忽视、被压制,甚至被磨灭.只有通过创造轻松愉快的课堂气氛和欢乐喜悦的学习环境,让他们勤于动脑,才能取得最佳的学习效果;同时鼓励学生动嘴说话,开发学生的口头表达能力,提高他们的交流水平,在开放的学习氛围下,学生的学习兴趣才能得到很大的提高.通过“研题”这样的课堂教学尝试,我们发现学生学习的主体意识增强了,愈来愈多的学生的潜能得到了开发与挖掘.学生在诸多方面得到了提高与进步.
4.2 高三数学课怎么上,才能上的出彩,才能让学生有所收获,有所进步?这是广大高三数学老师很共同关心的问题.如果高三课堂总是单纯的做了就讲,讲了又做,如此机械而又单调的重复,不但学生不爱听,老师也讲的乏味;老师讲的辛苦,学生听的辛苦,在这种大的课堂容量下,其教学效果却不尽人意.其主要原因是学生并没有真正动起来,也就是说学生的潜能没有得到发挥,学生的潜能早被这样的课堂模式淹没了.所以我们需要寻找唤醒学生潜能的课堂教学模式.通过“研题”这样的课堂教学尝试,我们发现原来老师不要讲得那么辛苦,学生也不要学的那么辛苦,而学习效果却是原来的很多倍.
4.3 让“研题”走进课堂,是我们课题研究组的一个尝试.当然,刚开始时,也没这么顺利,好多学生没有研究方法、思路,不会研究,只有少数优秀学生有想法而且敢讲,有的学生只会想不会讲,还有不少学生既不会想又不会讲,所以基本上都是老师在一步一步地启发;后来,随着“研题”次数的增多,学生的水平提高了,积累了一些经验,逐渐地学会了自主“研题”,上文所列就是较成功的一例.当然,这样喜人的状态是来之不易的,这需要老师长时间的努力与坚持.
1 中华人民共和国教育部.《普通高中数学课程标准(实验)》[M].北京:人民教育出版社,2012(111)
2 朱传美,迮兴国.《干嘛让常数参与运算?——一道模拟题讲解的课堂实录》[J].中学数学研究(江西),2014(7):18-20
本文为江苏省泰州市教科所“十二五”规划课题《高中数学课堂教学模式创新与学习方式转变的实验研究》(课题编号:TZJKS-YBLX2013123)的一个阶段性成果.
2016-12-18)
