深孔台阶爆破近区利用Anderson模型预测振动效应的修正方法研究

韩 亮， 梁书锋， 刘殿书， 辛崇伟

(1. 华北科技学院 安全工程学院，北京 101601； 2.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；3.北京科技大学 土木与资源工程学院，北京 100083)

深孔台阶爆破近区利用Anderson模型预测振动效应的修正方法研究

韩 亮1， 梁书锋2， 刘殿书2， 辛崇伟3

(1. 华北科技学院 安全工程学院，北京 101601； 2.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；3.北京科技大学 土木与资源工程学院，北京 100083)

在深孔台阶爆破近区利用Anderson模型进行波形叠加过程中，为了消除群孔脉冲序列及冲激响应存在的偏差，提出了预测振动效应的修正方法。按照不同间隔时间构建多种群孔脉冲序列，与冲激响应遍历进行卷积运算后，找出与实测波形最吻合的一组作为最优置信水平下的群孔脉冲序列；同时，基于主频衰减规律，以各炮孔至测点距离与基孔距离的接近程度作为确定冲激响应的方法。将其植入Matlab编制的预测程序对某次爆破振动效应进行预测。结果表明，修正后预测波形与实测波形的相似度提升显著，振速预测偏差由83%～130%下降到0%～39%，预测精度得到明显改善。

Anderson模型；近区；爆破振动；脉冲序列；冲激响应；预测；修正

自ANDERSON提出线性叠加理论后，在ANDERSON等[1-5]的努力下，振动效应的综合预测法得到了进一步的发展。该模型以实测单孔波形为基础，假设单孔波形在指定位置能够复现，同时假设群孔爆破的振动波形由单孔波形叠加而成，且每个炮孔爆破后产生的振动具有相同的时间源函数。根据爆破设计中各炮孔起爆延时，确定脉冲函数序列，通过一系列脉冲函数的输入，利用卷积理论计算出群孔爆破叠加波形。

计算过程涉及到两个参量：群孔脉冲序列和冲激响应。对于深孔台阶爆破，由于雷管延期误差的客观存在，各炮孔并不一定按照爆破设计的脉冲函数序列依次起爆；此外，近区地震波主频衰减较快，导致各炮孔在同一测点的冲激响应相差很大。上述两参量的偏差将影响卷积计算，进而导致预测得到的群孔叠加波形严重失真，无法反映质点振动的真实情况。

为了清除因雷管延期误差及近区地震波主频衰减较快带来的预测偏差，本文提出深孔台阶爆破近区群孔脉冲序列及冲击响应的确定方法，进而对Anderson模型的预测结果进行修正，并通过单排爆破试验对预测结果进行了验证。

1 基于波形识别的雷管延时确定方法

炮孔实际起爆时间是群孔脉冲序列的主要影响因素。本方法以现场实测与计算机分析相结合，按照不同间隔时间构建多种群孔脉冲序列，与冲激响应遍历进行卷积运算后，将一系列叠加波形与实测群孔波形进行比较，找出与实测波形最吻合的一组作为最优置信水平下的群孔脉冲序列，进而求出雷管延期时间。具体计算步骤如下：

(1)选择比对测点

地震波在传播过程中会受到断层、节理等地质构造的影响，传播路径越长，影响也越大。为避免上述问题，在考察比对测点时，应尽量选择受其影响小的测点，即与各炮孔均相距较近的测点。

(2)比对阈值的设定

比对阈值的设定应参考波形的时域特征，此处将振动幅值(振速)与幅值时域位置(时刻)作为双重判别参量，预先设置比对阈值，遍历判别结束后，再从触发结果中择优选取，其判别过程如式(1)和式(2)所示。

(1)

(2)

式中：k1～k4为触发条件；+Vs为叠加波形正向振速幅值，cm/s；+Vm为实测波形正向振速幅值，cm/s；-Vs为叠加波形负向振速幅值，cm/s；-Vm为实测波形负向振速幅值，cm/s；同理，+Ts为+Vs对应时刻，ms；+Tm为+Vm对应时刻，ms；-Ts为-Vs对应时刻，ms；-Tm为-Vm对应时刻，ms。

k1～k4的阈值范围为

0.9≤k1、k2≤1.1

(3)

0.9≤k3、k4≤1.1

(4)

在波形比对过程中，只有同时满足式(3)和(4)，该叠加波形才被触发，随后记录在临时数据库中。当所有群孔脉冲序列遍历运算结束后，系统再根据临时数据库的波形文件，选择最优波形，该波形对应的群孔脉冲序列，即为最优置信水平下的脉冲序列。

若比对过程中无叠加波形触发，说明在群孔叠加过程中，部分或全部炮孔地震波在传播过程中发生突变，也即传播路径的地质条件与单孔传播路径条件相差较大，该测点作为比对测点并不合适，应重新选取比对测点。

(3)波形到时的精确拾取

判别参量除了最大振幅，还包括最大振幅所在时刻。程序计算时，为了相互参照，是以实测波形的位置固定不变，各炮孔波形遍历叠加来比对的。因此，需要精确拾取实测波形及单孔波形的到时，这样才能保证二者的起点一致。若到时不准确，一方面，可能会对脉冲序列的计算精度产生影响，更有甚者，会出现无波叠加波形触发的情况。

(4)剔除各炮孔地震波的走时

计算得到的群孔脉冲序列，包含了炮孔的实际起爆时间以及炸药爆炸后地震波的传播时间。为了得到雷管的延期时间，需要在群孔脉冲序列中剔除掉地震波在各自传播路径上的走时。

综上，基于波形识别的雷管延时计算流程如图1所示。

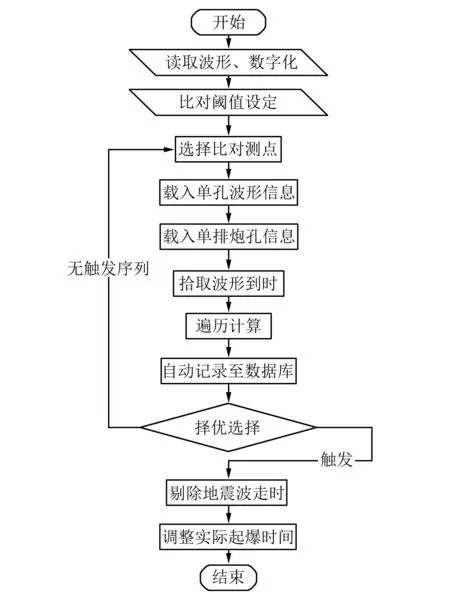
图1 雷管延期时间计算流程图Fig.1 Calculation flow chart of detonator delay time

2 同一测点各炮孔冲击响应的确定方法

群孔爆破中，各炮孔至同一测点的距离不同，当爆源分布范围较大时，差距将进一步拉大，这种情况在近区表现的尤为明显。一般来说，当测点间距相差不大时，地震波频率的变化可以忽略不计；但超过一定距离后，地震波的主频将发生明显变化，从而影响波形的叠加结果。

通过比较各炮孔至测点的距离，对基孔波形的频率进行修正。修正方法如下：

(1)计算各炮孔至所有测点的距离；

(2)对该场地条件下所有单孔波形的主频进行回归，求得主频衰减规律；

(3)当炮孔i与测点j的距离接近某一个基孔波形的距离、且该基孔波形的主频符合当前场地的主频衰减规律，可将此波形作为炮孔i至测点j的基孔波形；

(4)根据该场地条件下的振动衰减规律确定基孔波形的振动比例系数。

3 应用实例

3.1 工程概况

以北京凤山石灰石矿2015年12月11日爆破作业为例。现场爆破方式为排间起爆，为了不增加现场工作量及试验成本，单孔试验拟与爆破作业同时进行。其中，排间爆破为主爆区，优先起爆，排间延时110 ms；最后一排布置七个炮孔用于预测检验，与主爆区延时间隔拉大至490 ms；最末段为试验单孔，与最后一排炮孔延时间隔为380 ms。试验单孔与最后一排炮孔的爆破参数见表1。

表1 爆破参数

在爆区后方以最后一排第3孔为中心，共布置左、中、右三条测线，测点编号及测点距离见图2。

图2 现场测点布置示意图Fig. 2 Layout schematic diagram of measurement point

3.2 预测结果修正

(1)群孔脉冲序列修正

将提出的雷管延时确定方法应用于本例，选择3#测点作为比对测点，实测单孔波形与单排七孔波形如图3所示，此处单孔与单排波形均取垂向分量。

图3 3#测点处单孔与单排波形Fig.3 Waveform of single hole and single-row in 3# measuring point

构建单排七孔脉冲序列，在Matlab平台下编制程序，对所有序列组合遍历计算，得到最优脉冲序列与炮孔实际起爆时间，见表2。

表2 实际起爆时间计算

对每一个测点而言，将各炮孔的实际起爆时间与各自地震波走时累加，便得到了该测点处修正后的群孔脉冲序列，见表3。

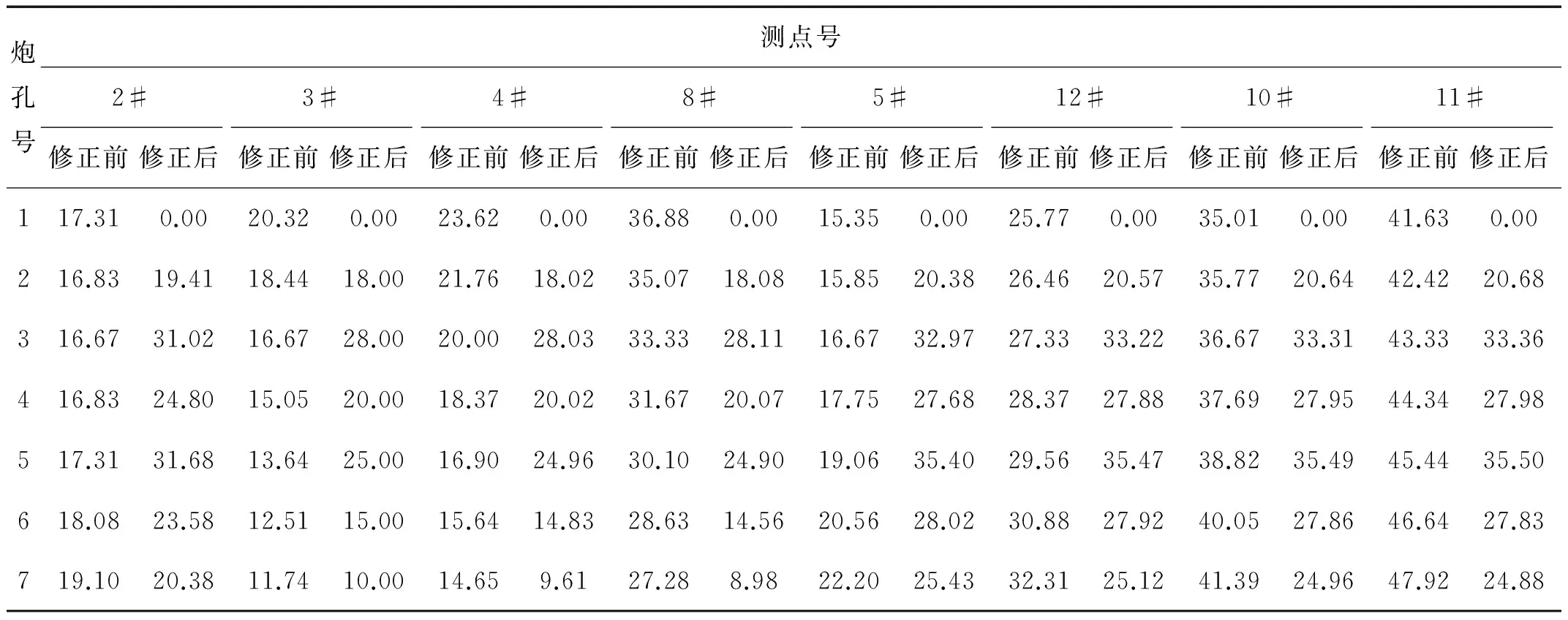
表3 单排七孔修正前与修正后的脉冲序列

(2)冲激响应修正

将第3节提出的确定冲激响应的算法植入Matlab程序，在利用ANDERSON模型计算单排孔叠加波形的过程中，可实现对各炮孔冲击响应的自适应修正。

3.3 修正前后预测结果对比

图4和图5反映了修正前后预测波形与实测波形的对比情况，表4反映了修正前后预测振速与实测振速的大小及偏差。从中可见，修正后各测点处预测波形与实测波形的相似程度显著增加，振速预测偏差从83%～130%下降到0%～39%，预测精度得到明显改善。总体来看，修正后的预测结果完全满足现场工程应用。

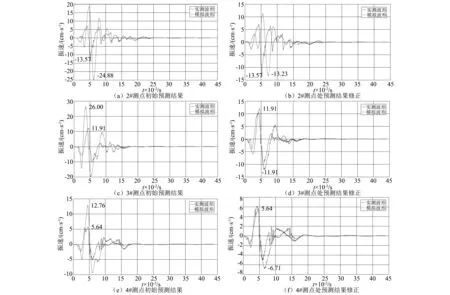
图4 预测结果修正前后对比Fig.4 Predicted results compared before and after correction

图5 预测结果修正前后对比Fig.5 Predicted results compared before and after correction

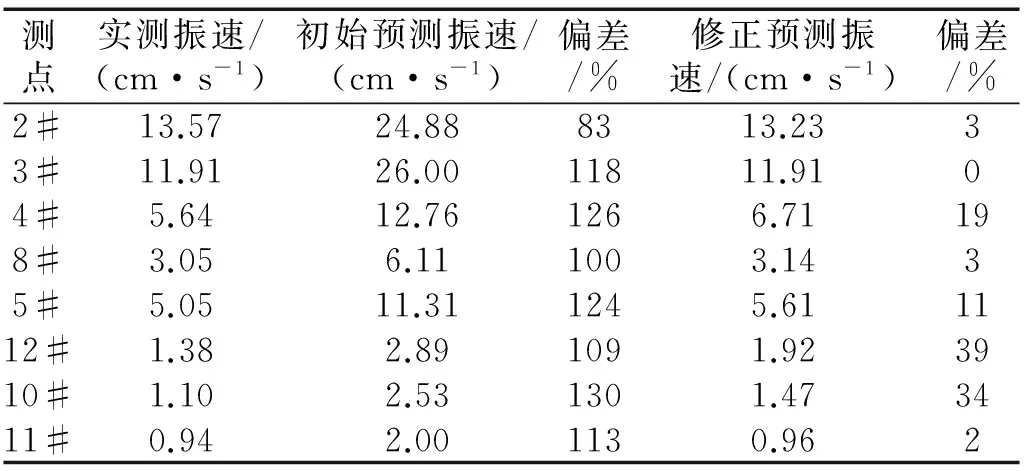
表4 预测结果及偏差修正前后对比Tab.4 Predicted results and deviation compared before and after correction

4 结 论

本文对深孔台阶爆破近区利用ANDERSON模型预测振动效应的修正方法进行了探索，通过单排爆破试验，验证了方法的可行性，全文结论如下：

(1)针对客观存在的雷管延期误差及近区变化较大的地震波主频，提出一种基于波形识别的雷管延期时间确定方法，以及同一测点各炮孔冲击响应的确定方法，两者结合可对振动效应的预测进行修正。

(2)以某次爆破作业为例，将修正算法植入Matlab编制的预测程序，结果显示，修正后预测波形与实测波形的相似度提升显著，振速预测偏差由83%～130%下降到0%～39%，预测精度得到明显改善。

[ 1 ] ANDERSON D A. A method site-specific prediction and control of ground vibration from blasting[C]//Proceedings of the First Mini-Symposium on Explosives and Blasting Research, 1985:28-42.

[ 2 ] HIZEN K G. Modelling of blast vibrations[J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1988, 25(6): 439-445.

[ 3 ] WHEELER R M. Controlling blast vibration effects with on-site analysis of single hole signatures “A new approach”[C]//Proceedings of the Fifth Mini-Symposium on Explosive and Blasting Researeh, 1989:123-134.

[ 4 ] RHOLL S A. Computer simulation to determine the effect of firing time scatter[C]//Proceedings of the Eighteenth Conference on Explosives and Blasting Techniques, 1999: 213-222.

[ 5 ] BLAIR D P. Blast vibration control in the presence of delay scatter and random fluctations between blastholes[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(2): 95-118.

[ 6 ] 吴从师,吴其苏. 爆破地震模拟初探[J].爆炸与冲击,1990,10(2):170-175. WU Congshi, WU Qisu. A preliminary approach to simulating blast vibration[J]. Explosion and Shock Waves, 1990, 10(2): 170-175.

[ 7 ] 卢文波,王进攻. 爆源中远区的爆破振动场模拟[J].爆破,1996,13(3):8-11. LU Wenbo, WANG Jingong. A simulation of blasting vibration in middle and far field of explosion source[J]. Blasting, 1996, 13(3): 8-11.

[ 8 ] 徐全军,毛志远,张庆明,等. 深孔微差爆破震动预报浅析[J].爆炸与冲击, 1998, 18(2): 182-186. XU Quanjun, MAO Zhiyuan, ZHANG Qingming, et al. The analysis of ground vibration prediction of delay-fired bench blasting[J]. Explosion and Shock Waves, 1998, 18(2): 182-186.

[ 9 ] 杨年华,张乐. 爆破振动波叠加数值预测方法[J]. 爆炸与冲击, 2012, 32(1): 84-90. YANG Nianhua, ZHANG Le. Blasting vibration waveform prediction method based on superposition principle[J]. Explosion and Shock Waves, 2012, 32(1): 84-90.

[10] 陈继强,刘为洲. 多孔爆破振动强度的单孔波形叠加计算[J].金属矿山, 2000 (8): 53-56. CHEN Jiqiang, LIU Weizhou. Single hole waveform superimposed calculation of the vibration strength of multihole blasting[J]. Metal Mine, 2000 (8) : 53-56.

[11] 甄育才,朱传云. 中远区微差爆破振动叠加效应影响因素分析[J].爆破, 2005, 22(2): 11-15. ZHEN Yucai, ZHU Chuanyun. Analysis on influential factors of vibration superposition in middle and far field of millisecond blasting[J]. Blasting, 2005, 22(2): 11-15.

[12] 刘军,崔清荷. 爆破振动效应预测方法新进展[J].河海大学学报(自然科学版), 2015, 43(5): 465-471. LIU Jun, CUI Qinghe. Advances in methods of predicting blasting-induced vibrations[J]. Journal of Hohai University(Natural Sciences), 2015, 43(5): 465-471.

[13] 刘军,吴从师,高全臣. 建筑结构对爆破震动的响应预测[J]. 爆炸与冲击, 2000, 20 (4) : 333-337． LIU Jun，WU Congshi，GAO Quanchen． A research on predicting structural responses to blasting vibration[J]. Explosion and Shock Waves, 2000, 20(4) : 333-337.

Study on correction method of forecasting the effects of vibration using Anderson model in near field of deep hole bench blasting

HAN Liang1，LIANG Shufeng2，LIU Dianshu2，XIN Chongwei3

(1. Safety Engineering College, North China Institute of Science and Technology, Beijing 101601，China;2. School of Mechanics & Civil Engineering, China University of Mining and Technology (Beijing), Beijing 100083，China; 3. School of Civil and Resources Engineering, University of Science and Technology Beijing, Beijing 100083，China)

In the process of using Anderson model to superimpose waveform in near field of deep hole bench blasting, in order to eliminate the deviation of the multi-hole pulse sequence and the impulse response, a correcting method of forecasting the effects of vibration was proposed. After constructing the multi-hole pulse sequence in accordance with different intervals, then traversing doing convolution with impulse response, the best fit of the measured waveform was found as the multi-hole pulse sequence under the optimal confidence level. Meanwhile, based on the frequency attenuation law, taking the proximity of the distance from each hole to the measure point and the base hole distance as the parameter for determining the impulse response. With the Matlab forecasting program implanted into the above methods to forecast one blasting vibration, the results show that after correction, the forecast waveform is significantly closer to the measured one and the velocity forecasting deviation drop from 83%-130% to 0%-39%, forecasting accuracy is significantly improved.

Anderson model; near field; blasting vibration; pulse sequence; impulse response; forecasting; correction

2016-08-02 修改稿收到日期： 2016-10-24

韩亮 男，博士，1985年生

刘殿书 男，教授，博士生导师，1960年生

TD235

A

10.13465/j.cnki.jvs.2017.07.017