基于生成微分方程的行星齿轮箱故障振动信号解调分析

李康强， 冯志鹏

(北京科技大学 机械工程学院， 北京 100083)

基于生成微分方程的行星齿轮箱故障振动信号解调分析

李康强， 冯志鹏

(北京科技大学 机械工程学院， 北京 100083)

行星齿轮箱振动信号具有明显的调制特点，幅值解调和频率解调分析能够有效提取其中的故障信息。生成微分方程(GDE)方法可以估计调制信号的幅值包络和瞬时频率，实现解调分析，但该方法需要信号满足单分量要求。实际行星齿轮箱振动信号通常由复杂多分量成分组成，为实现信号的幅值解调和频率解调分析，应用经验模式分解(EMD)将信号分解为单分量本质模式函数，基于生成微分方程计算瞬时频率和幅值包络，根据瞬时频率的波动特点选择本质模式函数作为敏感分量，由敏感分量的包络谱和瞬时频率的Fourier频谱识别故障特征频率。通过行星齿轮箱故障模拟实验数据分析验证了解调分析方法的效果。

行星齿轮箱； 生成微分方程； 幅值包络； 瞬时频率

行星齿轮箱结构紧凑，传动比大，承载能力强，在车辆、直升机和风力发电等装备中应用广泛。作为动力传动系统中的关键环节，行星齿轮箱一旦出现故障，会导致整个动力传动链失效甚至停机，造成严重后果。因此，研究行星齿轮箱故障诊断问题具有重要意义。

和普通的定轴齿轮箱相比，行星齿轮箱的结构和运转方式独特，振动信号成分复杂，具有明显的幅值调制和频率调制特征。在时域内，这两种成分之间为乘积关系，在频域内，整个信号的Fourier频谱为调幅和调频成分各自Fourier频谱的卷积，因此，行星齿轮箱振动信号的Fourier频谱具有复杂的边带结构[1-2]。但是，振动信号中调幅和调频成分的调制频率和齿轮故障特征频率密切相关，其中包含了故障信息。如果对振动信号进行幅值解调和频率解调分析，可以避免复杂的边带分析，准确识别调制频率，从而实现故障诊断。

ZAYEZDNY等[3]提出了基于生成微分方程的信号表示方法，利用信号、信号微分以及信号各种变换组合之间的关系描述信号的结构和性质。信号可以视为一个生成微分方程的一个解(例如，一个简谐振动信号可以视为一个质量-弹簧动力学系统振动微分方程的解)，而生成微分方程则可以视为信号一个映射。基于该思想，可以通过信号的各阶微分函数的非线性组合运算，估计其包络幅值和瞬时频率等信息，从而为行星齿轮箱的复杂调制振动信号的解调分析提供了一种潜在分析工具。

但是，基于生成微分方程的信号包络幅值和瞬时频率计算需要信号满足单分量要求，而实际行星齿轮箱振动信号成分复杂。为了解决这一问题，本文发挥经验模式分解在复杂信号分解方面的优势，将实际信号分解为多个本质模式函数，从而满足单分量的要求。

在经验模式分解和生成微分方程方法集成的基础上，可以准确估计敏感分量的包络幅值和瞬时频率，实现幅值解调和频率解调，从而识别故障特征频率诊断齿轮故障。

1 生成微分方程

生成微分方程是基于结构特性的一种信号描述方法。信号可以视为一个微分方程的部分解，通过一些数学工具，可以使得这个微分方程具有简洁的非线性形式，而通过简化的生成微分方程则可以重构原始信号[3-5]。

(1)

(2)

(3)

(4)

上面每个状态函数(式(1)～(4))都对应一个微分方程

(5)

(6)

(7)

(8)

将有关于状态函数的表达式

(9)

关于结构特性理论的三个重要基本定理：

定理1 任何一个具有n+1 个独立变量的n阶齐次微分方程均可通过以上四个基本状态函数(式(1)～(4))表述为包含新的n+1个独立变量(状态函数及其微分)的n阶状态函数的形式，而且通过非基本状态函数可以将它表述为更加简洁的形式。

定理2 任意一个二阶可微函数均可构造一个具有下列形式的生成齐次微分方程的形式

(10)

(11)

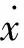
生成微分方程可以视为是信号的一种变换，通过这种变换可以将信号分解为一系列的微分方程的解的合集形式，从而估算能量、振幅和频率等信息。对于常见的调幅调频信号

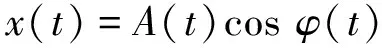
(12)

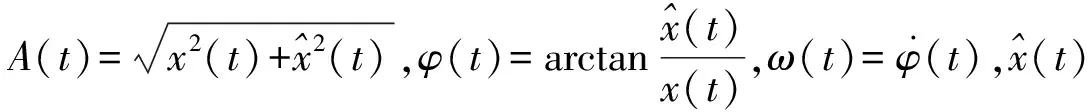
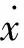
(13)

通常，调制信号的变化相比载波信号的变化要慢得多，此时A(t) 和φ(t) 相对于载波信号是缓变的，因此可以近似为常数。于是关于幅值和频率的状态函数可以近似δA=0，δω=0，kA=0。代入式(13)中可得瞬时频率和包络幅值的估计值

(14)

(15)

上述理论推导是对于连续信号而言的，对于离散信号，则需要将连续求解域划分为差分网格，用有限个节点代替原连续求解域，来获得原微分方程的近似解。中心差分的精度优于向前差分和向后差分，所以本文应用中心差分代替微分，使用中心差商代替导数

(16)

(17)

当步长Δt=1 时，可通过式(14)和式(15)求得离散信号瞬时频率和包络幅值的估计值

(18)

(19)

需要注意的是，生成微分方程方法只适用于单分量信号的解调分析。

2 分析步骤

行星齿轮箱的实际信号成分复杂，在应用基于生成微分方程的解调方法进行分析之前，需要将其分解为单分量成分。本文考虑经验模式分解在复杂信号分解方面的优势，提出了基于生成微分方程和经验模式分解的幅值解调和频率解调分析方法，具体分析步骤如下：

(1) 应用EMD分解方法把信号分解为多个IMF分量成分，满足生成微分方程的单分量要求。

(2) 应用GDE估计每个IMF分量的瞬时频率和幅值包络。

(3) 依据各IMF分量的瞬时频率波动特征，选择最先分解得到的而且瞬时频率围绕啮合频率或其倍频上下波动的本质模式函数作为敏感分量进行解调分析，原因有三：① 经验模式分解按照频率由高到低的顺序依次提取本质模式函数；② 齿轮故障引起的冲击特征在高频段内比较明显；③ 齿轮振动信号的载波频率为啮合频率或其倍频，瞬时频率围绕啮合频率或其倍频上下波动的本质模式函数包含齿轮故障信息。

(4) 对敏感分量的瞬时频率和幅值包络进行Fourier变换，根据包络谱和瞬时频率Fourier频谱中的峰值频率和各齿轮故障特征频率诊断故障。

3 仿真信号分析

根据行星齿轮箱的振动机理，其信号可以用调幅-调频信号模型描述[6-10]。不失一般性，假设太阳轮出现故障，只考虑齿轮啮合频率和故障齿轮的特征频率，则振动信号模型可表示为

x(t)=[1-cos(2πfsrt)][1+Acos(2πfst)]× cos[2πfmt+Bsin(2πfst)+φ]+n(t)

(20)

式中：fsr为太阳轮旋转频率，fs为太阳轮故障特征频率，fm为齿轮啮合频率。取fsr=1.2 Hz，fs=37 Hz，fm=200 Hz，A=B=1 分别为调幅和调频系数，初相位φ=0，仿真信号设置采样频率为3 000 Hz，加入信噪比为n(t)=6 dB 的Gauss白噪声。

图1(a)为该仿真信号的时域波形。图1(b)为使用EMD分解成的5个分量以及1个残量。使用生成微分方程估算各个分量的瞬时频率如图1(c)所示，可以看出第一个分量频率密集但是波动较大，第二个分量瞬时频率围绕齿轮啮合频率波动幅度较小，因此选择第二个分量进行分析。第二个分量的幅值包络如图1(d)所示。对瞬时频率估计值和幅值包络估计值进行Fourier变换以识别故障特征频率。结果如图1(e)和1(f)所示，其中图1(e)纵坐标表示的是瞬时频率的大小。可以很明显的发现太阳轮故障特征频率fs及其2倍频和受旋转频率fsr调制而产生的边带nfs±fsr，分析结果符合故障模型特征，验证了方法的有效性。

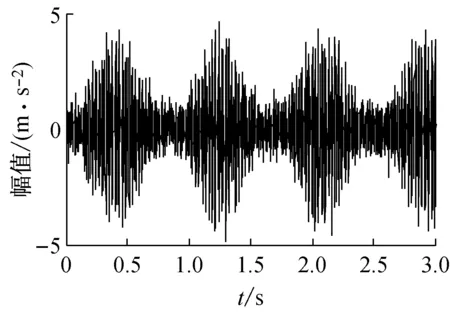
(a) 时域波形

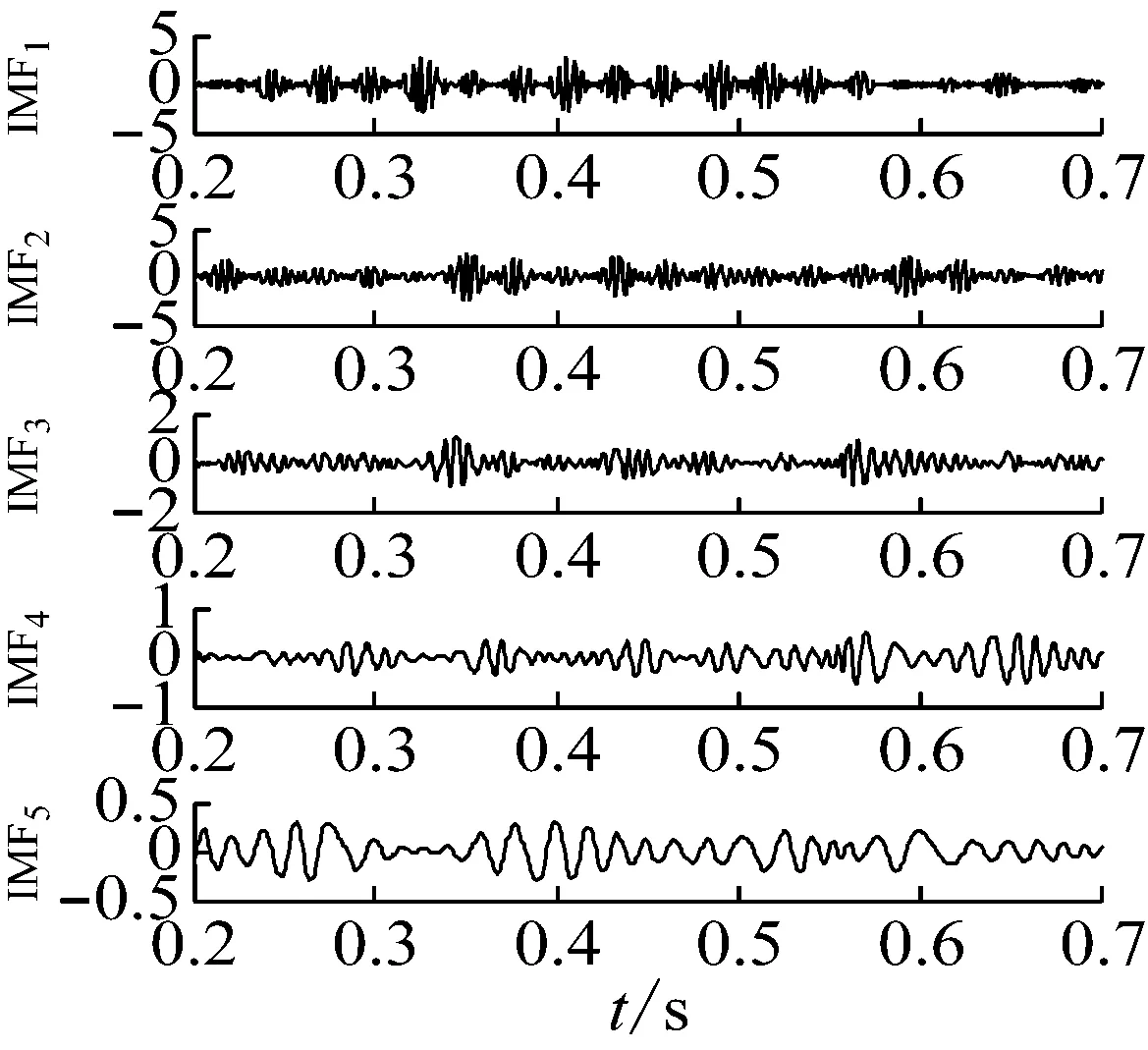
(b) EMD分解

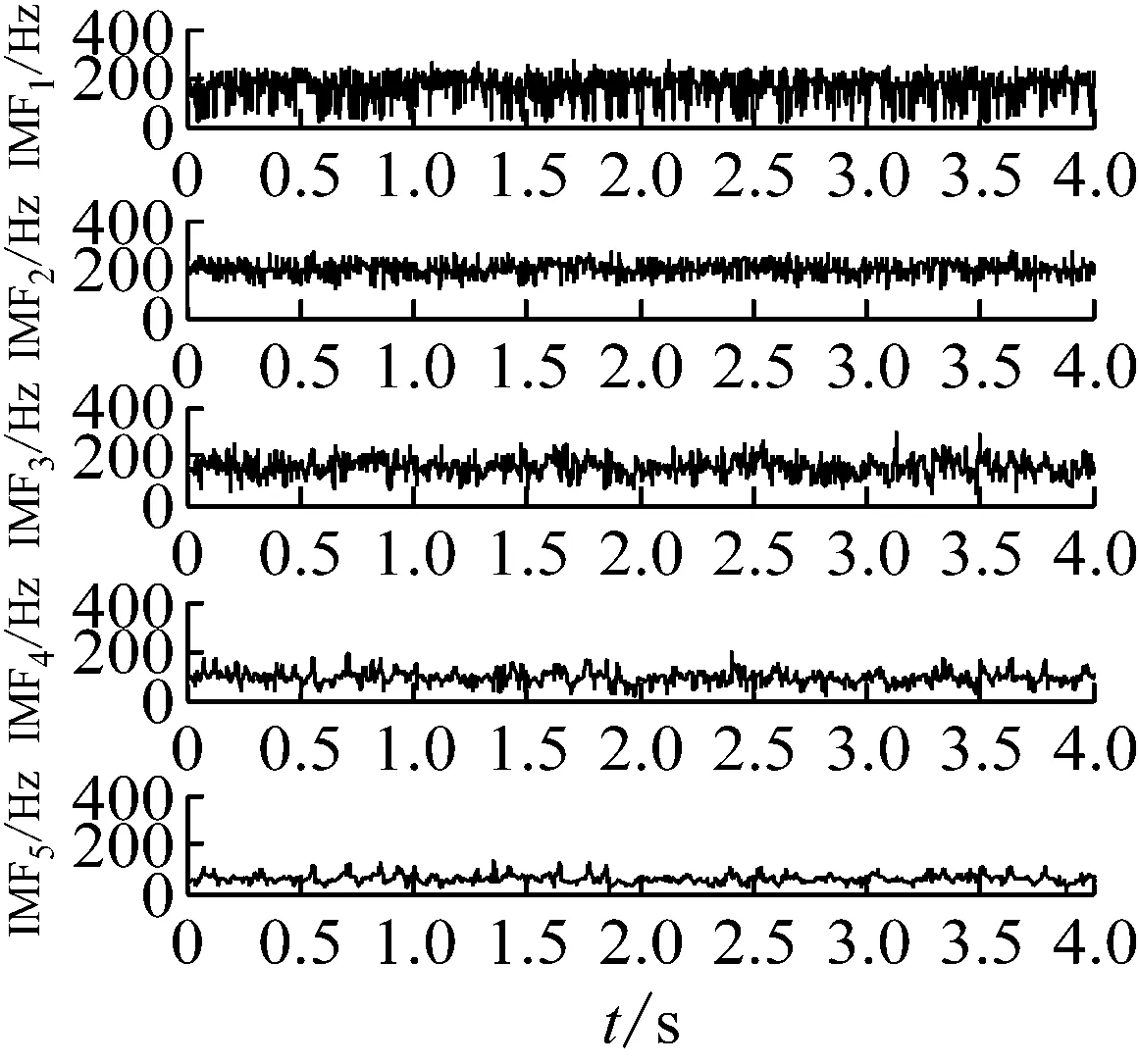
(c) GDE估计瞬时频率

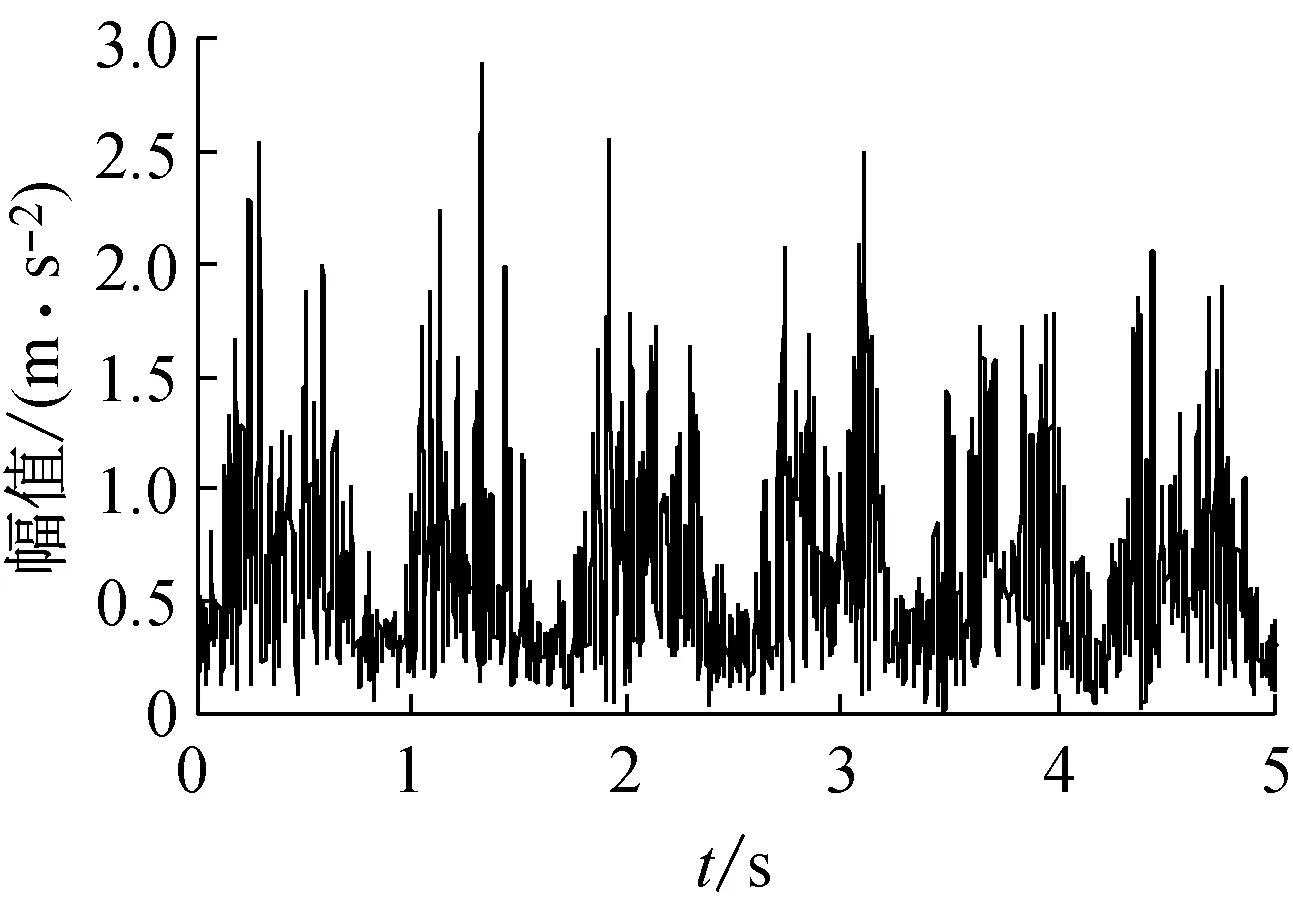
(d) 第二个分量幅值包络

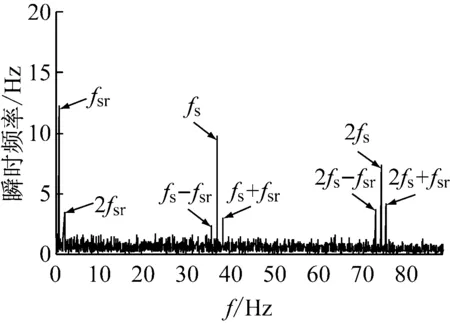
(e) 第二个分量瞬时频率Fourier频谱

(f) 第二个分量包络幅值Fourier频谱

4 实验信号分析

某行星齿轮箱实验系统如图2所示，由电机及其控制器、单级行星齿轮箱和振动测试系统组成。为了测试振动信号，在齿轮箱底座和箱体表面布置了多个加速度传感器，因为位于箱体顶部的传感器与太阳轮距离最近、传递路径最短所以包含了更多的信息，本文选取箱体顶部的传感器信号，信号采样频率为16 384 Hz。实验过程中，调整电机转速频率为15.95 Hz。根据齿轮箱的结构参数表1和输入转速，计算得到齿轮局部故障特征频率，见表2。

表1 行星齿轮箱参数

表2 特征频率表

图2 实验系统

4.1 正常信号

图3(a)为正常状态齿轮箱信号的时域波形，图3(b)为其EMD分解结果。对EMD分解结果进行生成微分方程瞬时频率和包络幅值估计，从图3 (c)可以看出第三个IMF的瞬时频率围绕啮合频率181.678 Hz上下波动，根据敏感分量的选取原则，选择该分量进行解调分析。在瞬时频率Fourier变换谱(图3(e))中，峰值主要出现在行星架旋转频率fc及其倍频以及和输入轴相连的太阳轮旋转频率fsr及其倍频等位置处。在敏感分量幅值包络的Fourier频谱(图3(f))中，峰值同样出现在行星架旋转频率及其倍频以及太阳轮旋转频率和它的三倍频处。正常齿轮箱由于零件的制造误差及微小缺陷和箱体装配的误差等因素影响，这些因素将产生调幅调频效应，使得振动信号解调谱中出现上述频率成分。

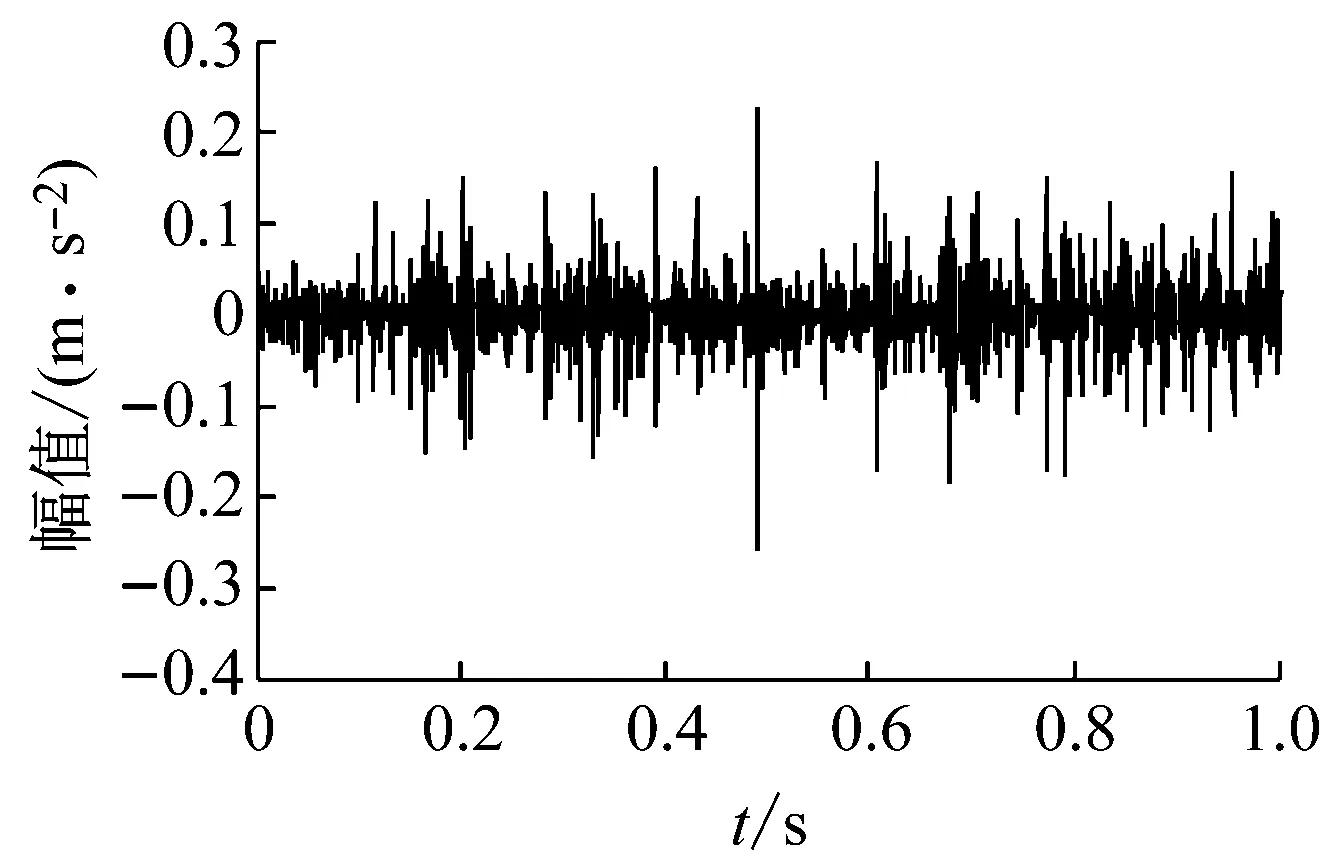
(a) 时域波形

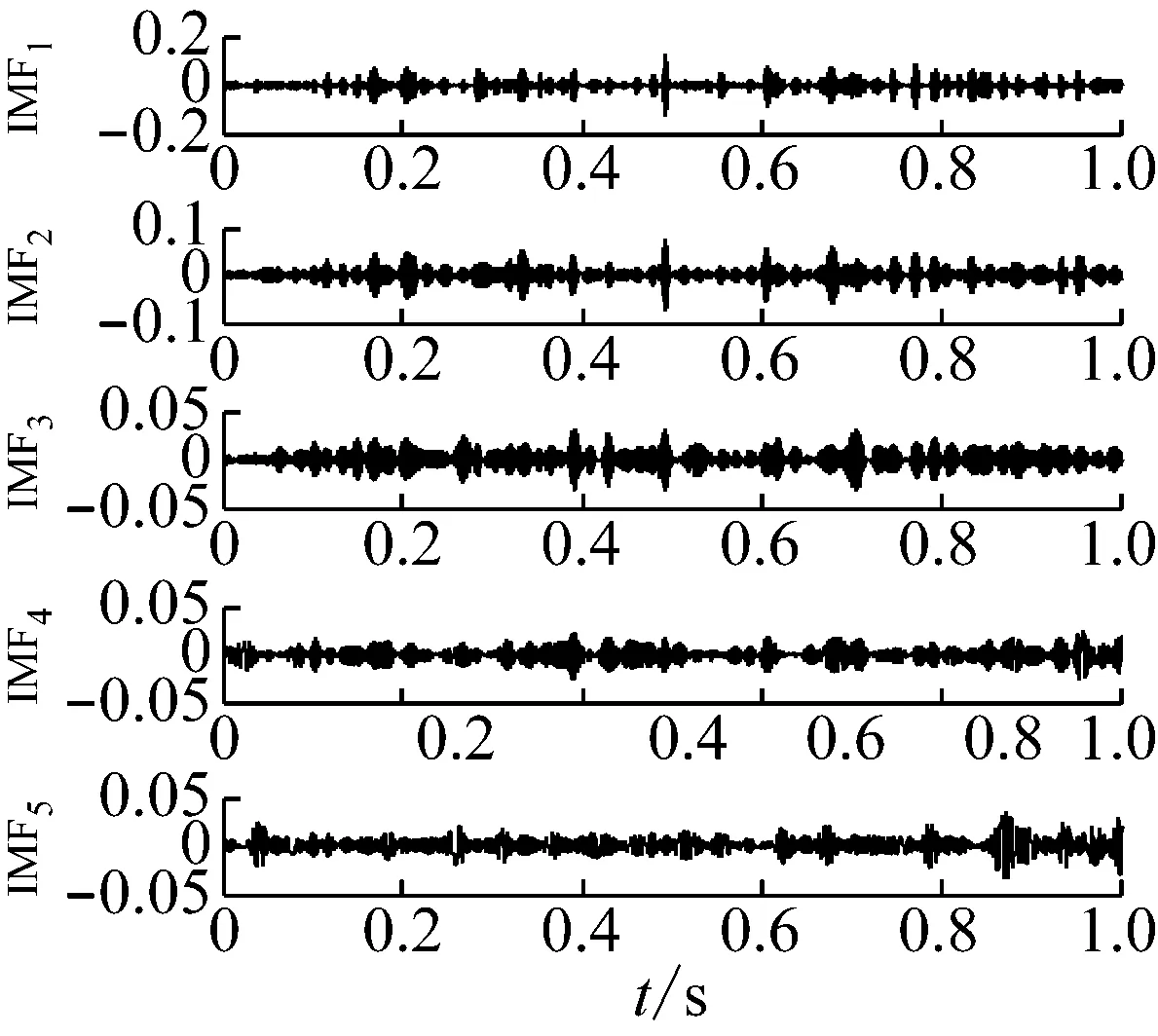
(b) EMD分解

(c) GDE估计频率

(d) 敏感分量幅值包络

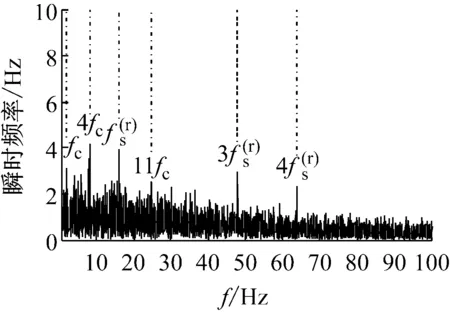
(e) 瞬时频率Fourier频谱

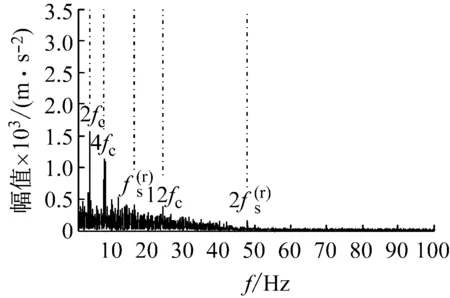
(f) 幅值包络Fourier频谱

4.2 太阳轮故障

为了模拟齿轮箱中太阳轮磨损故障，在太阳轮上的一个轮齿加工了磨损故障，如图4所示。

图5(a)为太阳轮故障振动信号时域波形，图5(b)为其EMD分解结果。对EMD分解结果进行生成微分方程瞬时频率和包络幅值估计，从图5(c)可以看出第三个IMF的瞬时频率围绕啮合频率181.678 Hz上下波动，根据敏感分量的选取原则，选择该分量进行解调分析。在瞬时频率Fourier变换谱(图5(e))中，行星架旋转频率fc及其倍频和太阳轮旋转频率fsr及其倍频依然存在，但是相比正常信号，太阳轮局部故障特征频率1/3fs倍频和行星架转频的组合及其倍频占主导地位，由于太阳轮同时与三个行星轮啮合，同时加工制作误差和微小缺陷会导致三个行星轮不可能完全一样，所以会出现太阳轮局部故障特征频率的1/3fs倍频和n/3fs倍频。在幅值包络Fourier变换谱(图5 (f))中，可以明显发现太阳轮故障特征频率fs，同样和瞬时频率Fourier频谱特征类似，太阳轮局部故障特征频率1/3fs倍频和行星架转频的组合及其倍频nfs±mfc占主导地位，这些特征说明太阳轮出现故障，符合实际情况。

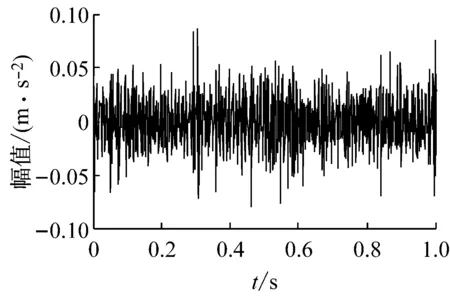
(a) 时域波形

(b) EMD分解

(c) GDE估计频率

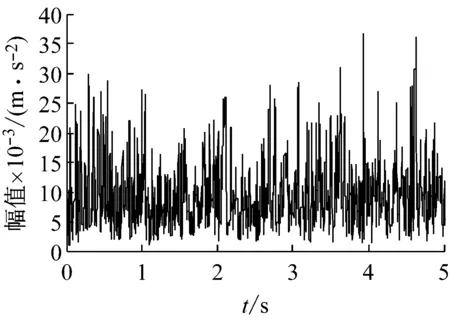
(d) 敏感分量幅值包络

(e) 瞬时频率Fourier频谱

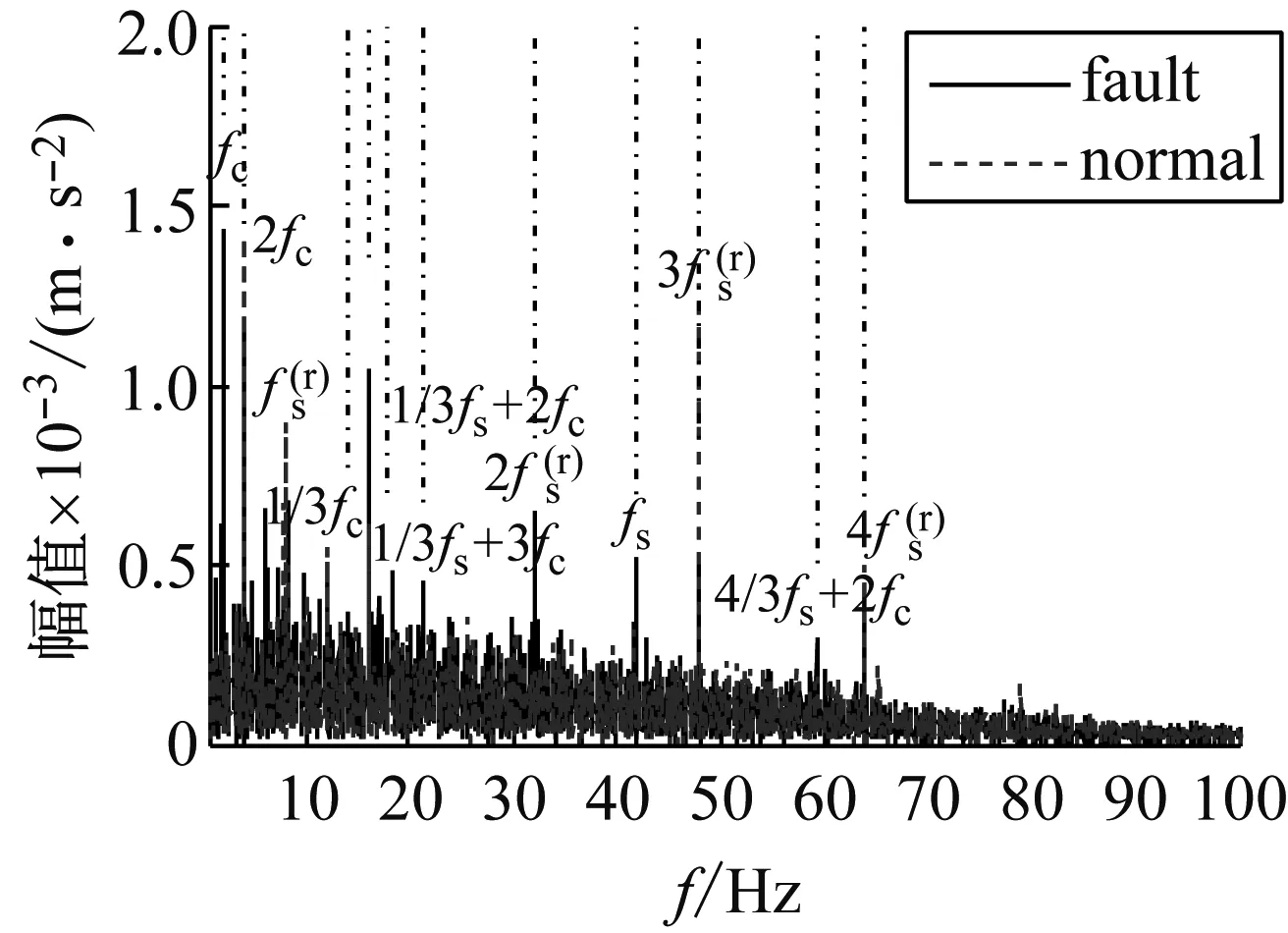
(f) 幅值包络Fourier频谱

4.3 行星轮故障

为了模拟齿轮箱中行星轮磨损故障，在行星轮上的一个轮齿加工了磨损故障，如图6所示。

图7(a)为行星轮故障信号的时域波形，图7(b)为其EMD分解结果。对EMD分解结果进行生成微分方程瞬时频率和包络幅值估计，从图7 (c)可以看出第三个IMF的瞬时频率围绕啮合频率181.678 Hz上下波动，根据敏感分量的选取原则，选择该分量进行解调分析。故障信号的瞬时频率的Fourier频谱(图7(e))的各个频率成分幅值明显大于正常信号，其中行星轮故障特征频率fp的三倍频和行星架旋转频率的组合3fp+fc占主导，其他峰值出现在行星轮故障特征频率的倍频及与行星架旋转频率的组合nfp±fc等位置，在幅值包络的Fourier变换谱(图7(f))中，行星轮故障特征频率fp及其倍频相比正常信号幅值更大更明显，这是因为行星轮的局部故障会造成不均匀的行星架载荷分配，使得行星架旋转对啮合振动的调频作用增强，导致行星架转频fc及其倍频的峰值增大，结果符合实际情况。

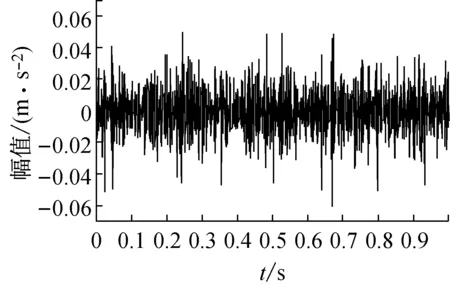
(a) 时域波形

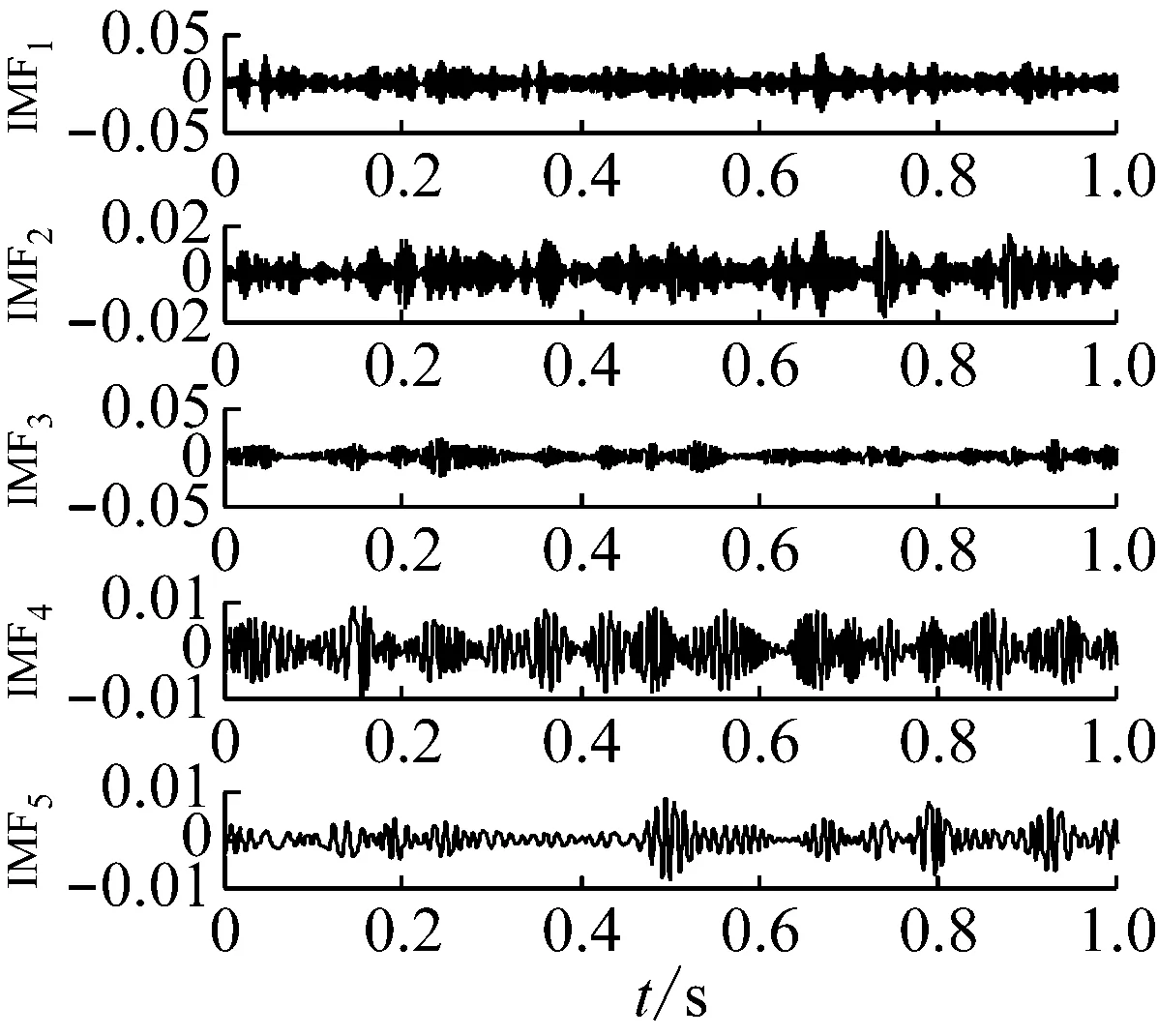
(b) EMD分解

(d) 敏感分量幅值包络

(e) 瞬时频率Fourier频谱

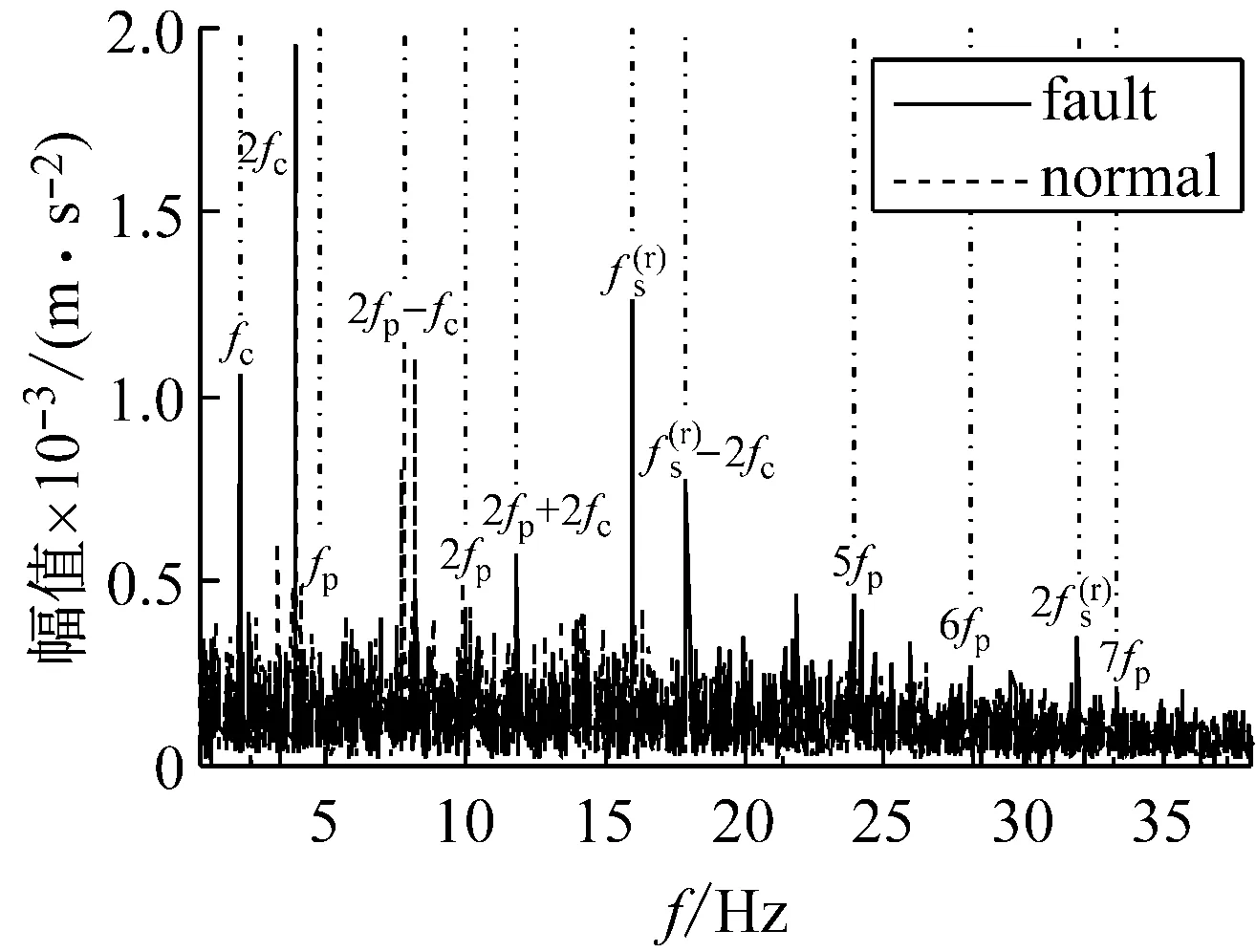
(f) 幅值包络Fourier频谱

4.4 齿圈故障

为了模拟齿轮箱中齿圈磨损故障，在齿圈上的一个轮齿加工了磨损故障，如图8所示。

图9(a)为齿圈故障信号的时域波形，图9(b)为其EMD分解结果。对EMD分解结果进行生成微分方程瞬时频率和包络幅值估计，从图9(c)可以看出第三个IMF的瞬时频率围绕啮合频率181.678 Hz上下波动，根据敏感分量的选取原则，选择该分量进行解调分析。由于加工误差和微小缺陷，实际中的三个行星轮不可能完全相同，所以齿圈故障特征频率的1/3fr及其倍频n/3fr的频谱幅值会增大，而我们的分析结果也证实了这一点，在瞬时频率Fourier变换谱(图9(e))上齿圈故障特征频率的1/3fr及其倍频明显大于正常值，而幅值包络的Fourier谱(图9(f))上也可以明显的发现齿圈故障特征频率fp及其三倍频、四倍频和五倍频。上述特征说明齿圈出现损伤，符合实际情况。

图8 齿圈局部损伤

(a) 时域波形

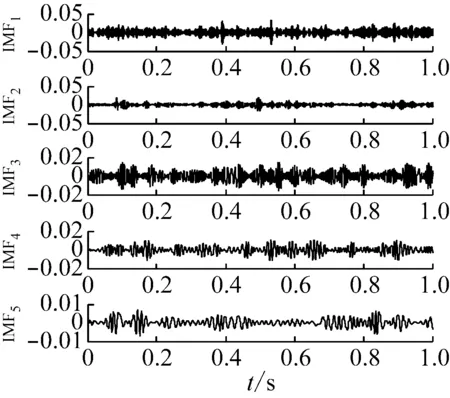
(b) EMD分解

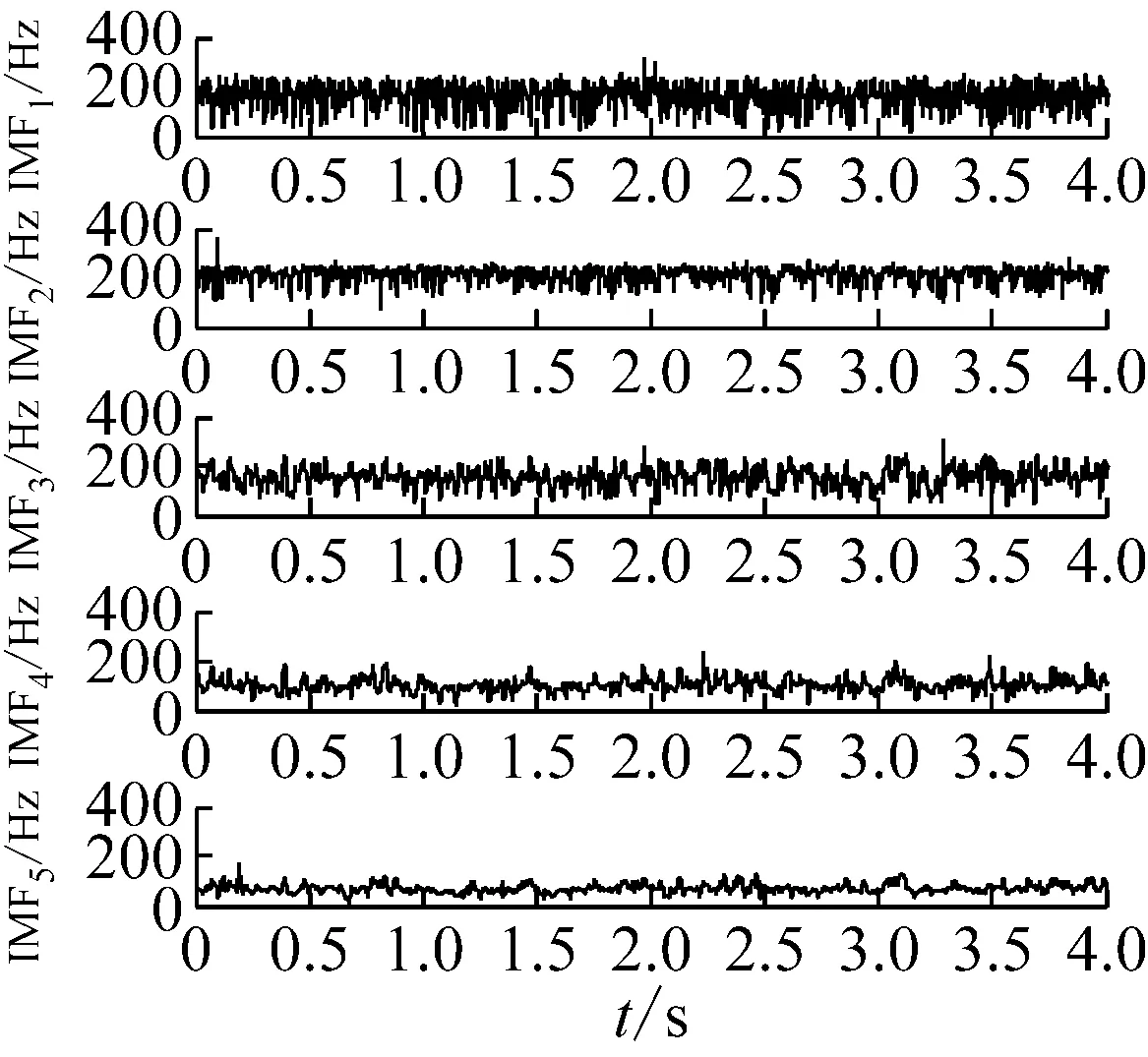
(c) GDE估计频率

(d) 敏感分量幅值包络

(e) 瞬时频率Fourier频谱

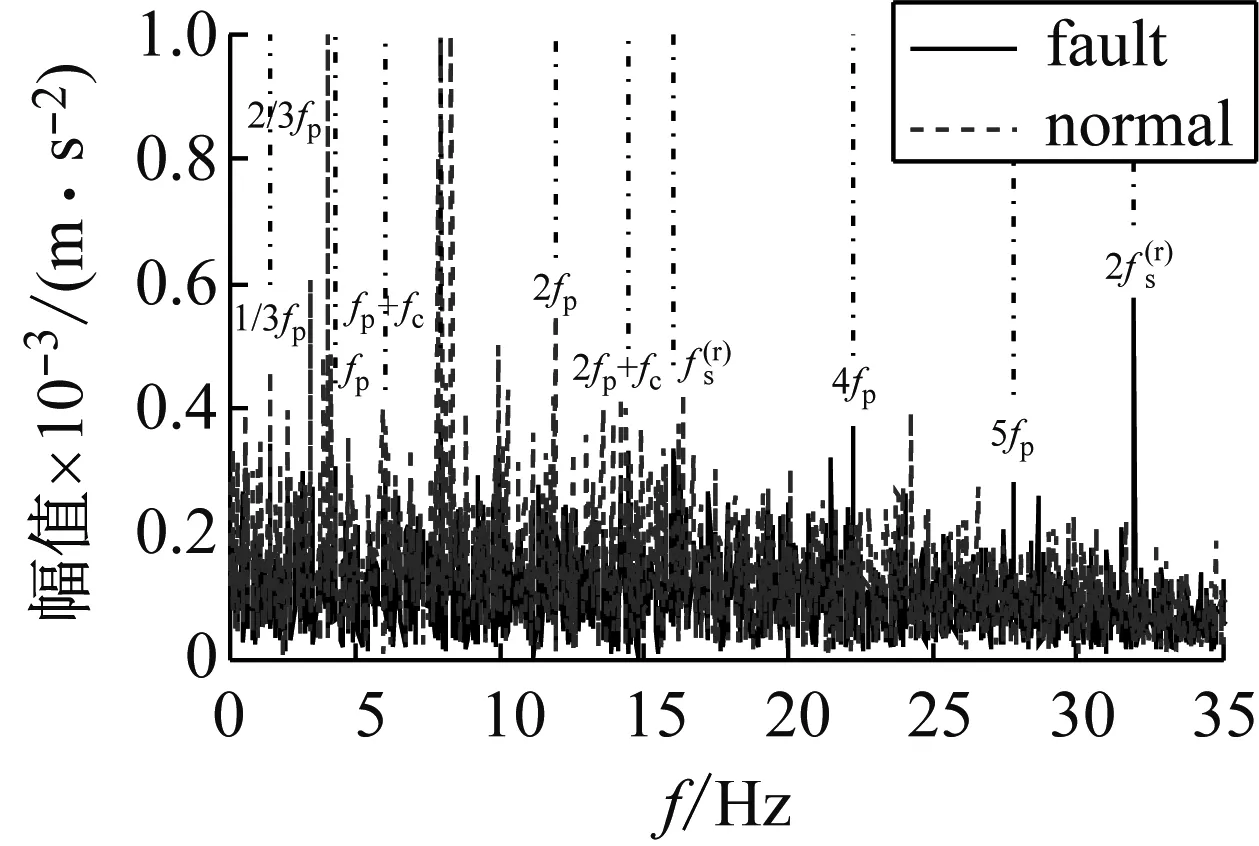
(f) 幅值包络Fourier频谱

5 结 论

本文将生成微分方程方法应用于行星齿轮箱的故障诊断中，分析了方法的基本原理与实现方法。依据第二节中的敏感分量选择原则选取EMD分解后的敏感分量后使用GDE方法来估计瞬时频率和包络幅值，算法简单，效果良好，适用性强。用行星齿轮箱故障仿真信号验证本方法后分析了实测实验信号，诊断出了太阳轮、行星轮和齿圈的局部损伤故障，验证了该方法的有效性，同时生成微分方程方法对于其他旋转机械如汽轮机、燃气轮机、风机、泵和发电机都有良好有效的诊断辨识能力。

[1] FENG Z P, ZUO M J, QU J, et al. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes[J]. Mechanical Systems and Signal Processing, 2013, 40 (1):56-75.

[2] FENG Z P, ZUO M J, ZHANG Y, et al. Fault diagnosis for wind turbine planetary gearboxes via demodulation analysis based on ensemble empirical mode decomposition and energy separation[J]. Renewable Energy, 2012, 47:112-126.

[3] ZAYEZDNY A, DRUCKMANN I. A new method of signal description and its applications to signal processing[J]. Signal Processing, 1991, 22(2): 153-178.

[4] ZAYEZDNY A, TIUNOV S. Extrapolation of time series by their structural properties[J]. Signal Processing, 1993, 32: 285-303.

[5] ZAYEZDNY A, TIUNOV S, BRONSTEIN A. Extrapolation of real-time processes by their structural properties[J]. Signal Processing, 1994, 38: 231-237.

[6] 冯志鹏，褚福磊．行星齿轮箱齿轮分布式故障振动频谱特征[J]．中国电机工程学报，2013，33(2)：118-125.

FENG Zhipeng，CHU Fulei．Vibration spectral characteristics of distributed gear fault of planetary gearboxes[J]．Proceedings of the CSEE，2013，33(2)：118-125．

[7] 冯志鹏，赵镭镭，褚福磊．行星齿轮箱齿轮局部故障振动频谱特征[J]．中国电机工程学报，2013，33(5)：119-127．

FENG Zhipeng, ZHAO Leilei, CHU Fulei．Vibration spectral characteristics of localized gear fault of planetary gearboxes[J]．Proceedings of the CSEE，2013，33(5)：119-127．

[8] 冯志鹏，赵镭镭，褚福磊．行星齿轮箱故障诊断的幅值解调分析方法[J]．中国电机工程学报，2013，33(8)：107-111．

FENG Zhipeng, ZHAO Leilei, CHU Fulei．Amplitude demodulation analysis method for fault diagnosis of planetary gearboxes[J]．Proceedings of the CSEE，2013，33(8)：107-111．

[9] 冯志鹏，褚福磊．行星齿轮箱故障诊断的频率解调分析方法[J]．中国电机工程学报，2013，33(11)：112-117．

FENG Zhipeng, CHU Fulei. Frequency demodulation analysis method for fault diagnosis of planetary gearboxes[J]．Proceedings of the CSEE，2013，33(11)：112-117．

[10] MC-FADDEN P D．Detecting fatigue cracks in gears by amplitude and phase demodulation of the meshing vibration[J]．Journal of Vibration Acoustics Stress and Reliability in Design-Transactions of the ASME，1986， 108：165-170．

Signal demodulation via the generating differential equation method for planetary gearbox fault diagnosis

LI Kangqiang, FENG Zhipeng

(School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

The vibration signal of a planetary gearbox has clear characteristics of modulation and analysis of frequency demodulation and amplitude demodulation plays a vital role in the fault diagnosis. Though the generating differential equation (GDE) method can estimate the amplitude envelope and the instantaneous frequency of the modulation signal, it only suits to single component composition. Actually, vibration signal of a planetary gearbox is composed of complex component composition. In order to analyze amplitude envelope and instantaneous frequency of a modulation signal, in this paper, we decomposed a modulation signal into the single component intrinsic mode function (IMF) by the empirical mode decomposition (EMD). According to the fluctuation characteristics of instantaneous frequency which result from the generating differential equation, the IMF as the sensitive component was chosen. The characteristic frequency of localized fault was identified with Fourier frequency spectrum of amplitude envelope and instantaneous frequency. Its effectiveness in extracting the characteristic frequency of localized fault was validated by the demodulation analysis of experiments of the planetary gearbox.

planetary gearbox; generating differential equations; amplitude envelope; instantaneous frequency

国家自然科学基金资助项目(11272047; 51475038); 教育部新世纪优秀人才支持计划项目(NCET-12-0775)

2016-01-07 修改稿收到日期：2016-03-07

李康强 男，博士生，1987年生

冯志鹏 男，博士，教授，博士生导师，1973年生

TH165+.3; TH132.425

A

10.13465/j.cnki.jvs.2017.08.002