基于非局部应变梯度欧拉梁模型的充流单壁碳纳米管波动分析
2017-04-20余阳,杨洋
余 阳, 杨 洋
(昆明理工大学 工程力学系, 昆明 650500)
基于非局部应变梯度欧拉梁模型的充流单壁碳纳米管波动分析
余 阳, 杨 洋
(昆明理工大学 工程力学系, 昆明 650500)
将非局部弹性理论和应变梯度理论结合,再根据流体滑移边界理论,建立了考虑流体和固体小尺度效应的充流单壁碳纳米管(SWCNT)流固耦合动力学模型,分别以非局部应力效应、应变梯度效应和流体滑移边界效应模拟微观小尺度效应对系统的影响,推导得出充流单壁碳纳米管的Euler-Bernoulli梁波动控制方程。通过对控制方程的求解,分析材料不同类型尺度效应对充流碳纳米管的振动和波动特性影响。结果显示,应变梯度效应和流体边界效应对低频波动起促进作用,对高频波动起阻尼作用,应力非局部效应则对波动始终产生阻尼作用。三种尺度效应对低流速系统的振动有促进作用,而对高流速系统产生阻尼作用。
非局部应力; 应变梯度; 碳纳米管; 流体边界效应; Euler-Bernoulli梁; 振动特性
碳纳米管在20世纪90年代早期被发现后[1],就凭借其优越的力、热、光、电及化学特性,成为了科技领域最受关注的功能材料之一[2-5]。在碳纳米管各项性能研究中,充流碳纳米管的动力学特性,是直接影响碳纳米管工程应用的主要性能之一,有关这方面的研究和报道层出不穷。研究充流碳纳米管力学性能的方法很多,主要分为实验手段和数值模拟方法两大类。实验手段由于在实际操作和精度控制方面有很大困难,应用受到限制。因此关于充流碳纳米管动力学特性的理论计算方法,成为了该领域的研究热点。基于这样的背景,发展出很多基于材料科学和力学理论的模型与分析手段。
在这些理论模拟方法中,分子动力学模拟,是可信度和公认度较高的方法。KRISHNA等[6]用分子动力学模拟了单壁碳纳米管内水分子的物理行为;CUI等[7]通过分子动力学模拟研究了纳观尺度的焊接;WANG等[8]也通过分子动力学模拟研究了充流碳纳米管表面的结构和热力学性能。
然而,分子动力学模拟由于需要考虑体系中每一个分子或原子和相邻粒子的作用势,这使得计算过程复杂而冗长,在时间和空间上都受到很大限制[9-10]。为了克服分子动力学模拟的不足,充流碳纳米管流固耦合系统的经典连续介质模型已经被大量应用。YAN等[11-14]在经典连续介质模型的基础上,研究了多壁碳纳米管的稳定性以及动力学特性;YOON等[15]也同样应用经典连续介质模型,研究了充流的悬臂碳纳米管的振动特性以及稳定性。
然而,经典连续介质模型无法模拟碳纳米管在微纳观环境下的小尺度效应,这些尺度效应包括静电引力、表面效应、分子间长程作用力等,这些尺度效应对材料力学特性的影响很大,不能忽略,这也就制约了连续介质模型的应用[16]。
发展适用于模拟碳纳米管尺度效应的连续介质力学模型,使其同时具有经典力学模型计算简单有效的特点,是相关学者目前普遍采用的方法。其中一个典型的模型便是ERINGEN的非局部连续介质弹性模型。该模型既可以模拟微观尺度效应对纳米结构体的影响,又有着计算简洁有效的特点。以非局部应力场模型模拟充流碳纳米管力学特性的研究报道屡见不鲜,比较典型的研究成果主要有:BAHAADINI等[17]使用非局部Euler-Bernoulli梁理论建立充流碳纳米管自由振动控制方程,研究了基于非局部弹性和滑移条件的黏弹性悬臂充流碳纳米管的自由振动和颤振稳定性;ZHEN等[18]基于非局部弹性理论和Euler-Bernoulli梁理论,应用了多维的Lindstedt-Poincaré方法,研究了单壁充流碳纳米管的非线性振动;ZEIGHAMPOUR等[19]应用了Donnell壳模型和修正的双剪理论,研究了双壁充流碳纳米管的振动及稳定性;DENG等[20]应用了非局部弹性Flugge壳模型研究了充流多壁碳纳米管的振动特征;FILIZ等[21]将碳纳米管模拟成功能梯度梁,研究了充流的嵌入式碳纳米管波的振动;LI等[22]基于非局部应力场梯度理论和Kelvin-Voigt黏弹性模型,推导出了黏弹性充流单壁碳纳米管波振动的控制方程;ALI-ASGARI等[23]基于非局部理论和von Karman拉伸的耦合,研究了充流碳纳米管的固有频率和非线性响应。除此之外,相关报道还有很多。
虽然ERINGEN的非局部连续介质理论在充流碳纳米管的力学分析中应用很广,但是模型的准确性与合理性在研究高频波的方面不尽如人意[24],且非局部弹性模型模拟显示碳纳米管刚度会随尺度效应增加而降低。这与实验结果和应变梯度理论模拟的结果相反[ 25-28]。
由于尺度效应对碳纳米管的应力和应变都有影响,非局部理论仅从应力角度分析尺度效应是不够的。AIFANTIS提出以应变梯度弹性理论分析尺度效应对材料应变的影响,可以准确模拟材料的应变尺度效应。而CHEN等[29]以应变梯度理论计算的分子间力与分子动力学模拟结果吻合很好。由此可见,为了能够模拟两种尺度效应对充流碳纳米管流固耦合系统的动力学特性影响,需将两种理论结合建模。CHALLAMEL[30]运用了应变梯度弹性模型和ERINGEN的非局部弹性模型,讨论了小尺度效应在振动分析中的主要特性,SONG等[31-32]结合非局部弹性模型和应变梯度模型,研究了纳米结构在初始轴向应力作用下波动的离散关系以及碳纳米管在自由空间和固定在弹性介质中横向波的特性。 LIM等[33]将高阶非局部弹性理论和应变梯度理论结合建模,得到了分析碳纳米管波动特性的梁模型控制方程和边界条件,并以此讨论了尺度效应对梁模型各项波动参数的影响规律。LI等[34-36]在结合非局部理论和应变梯度理论的基础上,分析了功能梯度梁结构的屈曲、波传导行为,以及在磁场中材料表面效应对波传导的影响规律。除此以外,对于微观流固耦合系统的力学特性分析,以及流体受到的尺度效应的研究,还鲜有报到。考虑到微纳观流体的性质对材料科学的发展至关重要,研究分析流体的尺度效应将有重要意义。
本文将应用LIM的“非局部应力与应变梯度耦合本构关系式”分析微观环境中碳纳米管的应力/应变关系,同时以流体边界滑移理论分析管腔内流体的尺度效应,根据Euler-Bernoulli梁理论建立充流碳纳米管流固耦合动力学模型,推导系统的波动控制方程。通过对控制方程求解,分析该系统的自由振动和波动特性,分别探索流体和固体材料的尺度效应对系统各项动力特性的影响规律。
1 充流单壁碳纳米管流固耦合动力学模型
将单壁碳纳米管置于三维笛卡尔坐标系中,管腔内部充满流体并匀速流动,流速为U,如图1所示。图中L和w分别为管长和横向挠度,x和y分别为轴向和横向坐标。

图1 充流单壁碳纳米管
根据LIM的研究结果,非局部弹性应力本构和应变梯度本构经耦合后,得到新型碳纳米管应力/应变本构方程为
(1)

(2)
对于一维Euler-Bernoulli梁模型,如果仅仅考虑x方向上的正应力与正应变,那么式(2)可进一步简化为
(3)
式中:σ(x),ε(x)分别代表应力和应变函数。
在SWCNT梁横截面Ac上的弯矩为
(4)
Euler梁理论中应变与挠度的关系式为
(5)
将式(3)两边积分,并将式(4)和(5)代入式(3),可得:
(6)
式中:I=∫y2dAc,为横截面惯性矩。对式(6)所示偏微分方程中的弯矩M求解,可得:

(7)
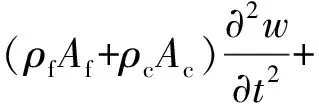
(8)
式中:ρf,ρc分别为流体与碳纳米管的密度;Af,Ac分别为流体和碳纳米管所占的横截面面积;U为管腔内流体的流速。
根据流体边界理论,在微纳米尺度下,流体处于滑移区域,其流速在管壁处受到小尺度效应影响而变化[38]。RASHIDI等[39]将受到尺度效应影响的流速与正常流速U的关系式简化为
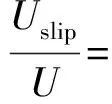
(9)
式中:Uslip为流体受到尺度效应影响的流速;ξv为径向弯矩调节系数;VCF为Uslip和U的比值;Kn为Knudsen数,其取值表示小尺度效应对流体流速的影响程度;a是式(9)中的一个系数,a的取值为
(10)
式中:b为一般滑移系数,可取为-1。
由式(9)和(10)可见,Kn值可以定量模拟流体边界效应对流速的影响,该结论已在相关文献中得到证实和应用[39-41]。将式(7)和(9)代入控制式(8)中,得到考虑流体边界条件和固体尺度效应的充流碳纳米管自由振动控制方程:
改进后的弹力绷带小手套和普通弹力绷带小手套应用方式基本相同,除了不同类型的绷带小手套有不同的拆除和固定方式外,改进后的弹力绷带小手套最大的特点是能够将着力点固定在患儿的大拇指部位,这样即使是患儿移动腕关节和手指关节,也不会轻易出现留置针移动、脱落、卷边等现象。此外,护理人员也加强了对患儿的巡视和检查,并观察患儿固定位置皮肤是否出现了异样情况。
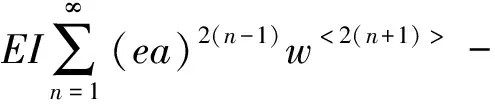
(11)
将式(7)代入经典充流Euler梁模型的三种边界条件,可得充流碳纳米管边界条件为
简支边界条件:
(12a)
(12b)
固定边界:
固定边界的自然边界条件为
(13a)
(13b)
自由边界:
自由边界的自然边界条件为
(14a)
(14b)
考虑到式(7),且在微观环境中ea≠0,进一步整理后可得:
简支边界条件:
(15)
固定边界:
(16)
自由边界:
(17)
忽略式(11)中高阶项ο((ea)4),控制方程简化为
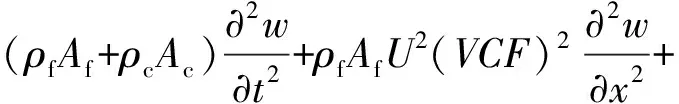
(18)
通过对式(18)求解,可对充流碳纳米管流固耦合系统各项动力特性进行分析。
2 波动分析
由于碳纳米管自由振动可简化为简谐波动,于是将式(18)的解定义为
(19)
式中:k为波数;ω为波动角频率;W为振幅。将式(19)代入式(18)得
-(ρfAf+ρcAc)ω2+2ρfAfU(VCF)ωk-ρfAfU2(VCF)2k2-EI(ea)2k6+EIk4-EIl2(ea)2k8+EIl2k6=0
(20)
式(20)为关于ω的一元二次方程,其解为
(21)
而在式(21)中
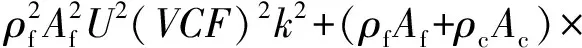
(22)
很显然,角频率的值取决于波数k,流速U,非局部参数ea, Knudsen数Kn还有应变梯度参数l。如果Δ<0,那么角频率的值就将是一个复数,在这种情况下,可以将角频率值的实部和虚部表示为
(23)
(24)
3 结果与讨论
碳纳米管的动力学特性(角频率ω)受波数k,流速U,非局部参数ea, Knudsen数Kn还有应变尺度参数l的共同影响,具体变化规律可由式(21)~(24)定量分析。分析计算时,取碳纳米管的几何尺寸和材料的常数为[42]:E=1 TPa,Af=3×10-19m2,Ac=3.63×10-19m2,I=1.78×10-38m-4,ρf=1×103kg/m3,ρc=2.27×103kg/m3。
图2所示为非局部尺度参数ea取0.05 nm、0.1 nm和0.2 nm时,波数k与频率之间的变化关系。从图2可以看出,不论当ea取何值,频率的变化趋势相同,即频率先随波数升高而增大,但当波数达到某一临界值时,频率急剧下降,表现出很强的波动阻尼效应。该临界波数的大小则随ea的不同而不同。如图2所示,当ea取0.2 nm、0.1 nm和0.05 nm时,临界波数kc的取值分别为: 4.3×109m-1、8.5×109m-1和17.5×109m-1。进一步观察发现,临界波数和相应的ea取值之间的乘积相同,即ea×kc=常数。分析原因,主要是因为引起频率降低的因素是当波数较大,波长较短时,非局部效应的影响区域超过了一个波长范围,即1/kc>ea,能量在传递了一个周期后,仍然没有出非局部区域,从而使得继续传递受阻,振动衰减明显[42-44]。而随着ea的增加,非局部区域范围扩大,要在一个波长范围内超出非局部区域,则需要波长增加,波数降低。当波长较大时,能量在传递一个周期后,已出非局部区域,相应的衰减效应不再出现,而刚度增加效应得以体现,所以出现了低波数区频率增加的现象。类似的结论在内部无流体的碳纳米管振动时也得到证实,证明在波长较大时,随着非局部尺度参数ea的升高,碳纳米管的刚度是增加的。

(a) 整体图

(b) 局部图
图3显示的是在波数取k=1×109m-1,ea取值不同时,SWCNT管腔内流体流速与SWCNT自由波动频率实部之间的变化关系。首先,由图3可以看出在相同的流速下,随纳观尺度参数ea逐渐变大,碳纳米管波动频率会有变小的趋势,说明当非局部尺度效应增加时,SWCNT梁刚度下降,波动阻尼增强。据图3所示,随着流速的增加,SWCNT梁波动频率是增加的,证明在流速较低时,对波动和振动有促进作用,这种动力特性与宏观流体结构类似。然而,当流速超过1 500 m/s之后,频率就会随着流速的增大而急剧降低,而当流速达到U=2 900 m/s时,频率就会变成复数,说明波动衰减明显,该结论与流速较低时的动力特性相反。发生波动衰减的主要原因,是随着流体流速升高,流体分子运动加快,分子动能增加,分子间相互作用力增强,造成系统内尺度效应增强,从而导致碳纳米管刚度下降,波动阻尼增大。
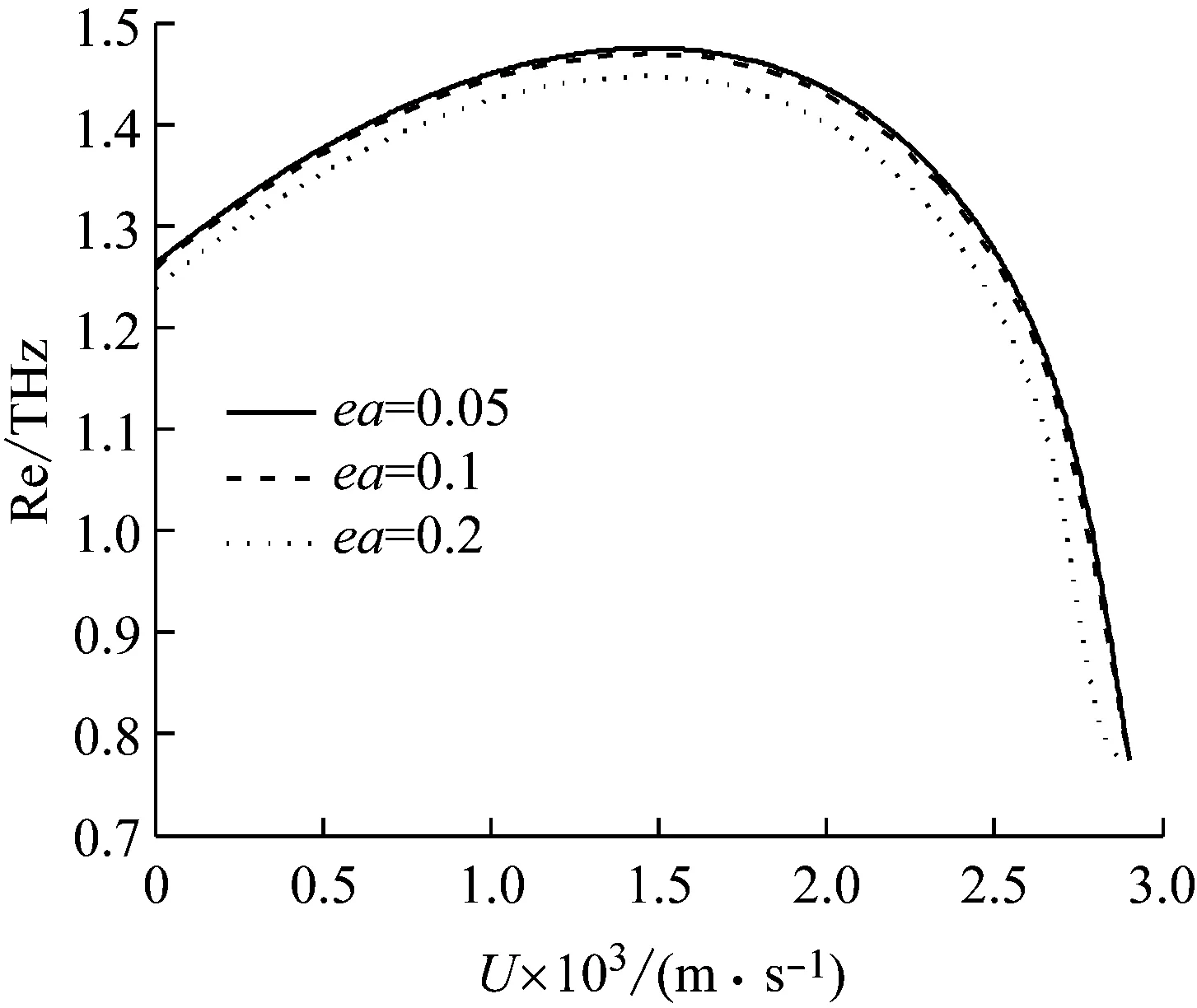
图3 频率实部与流速、纳观尺度参数的变化关系
图4显示了当波数分别取k=1×109m-1、k=2×109m-1和k=5×109m-1时,流速与SWCNT波动频率的变化关系。可以看出来频率变化是很大的。当波数变化时,流体的临界流速增加,但总体的趋势仍然是在临界流速之前,振动频率随着流速的增大而增大,而在临界流速之后,振动频率随着流速增大而减小。所以,增大波数、减小波长对于促进SWCNT梁波动频率明显效果。
图5显示了碳纳米管应变梯度参数分别取l=10 nm,20 nm,50 nm时,非局部尺度参数ea与振动频率实部之间的变化关系。随着ea逐渐变大,频率的变化幅度是非常小的,但仍然可以看出有略微减小的趋势。从图5可以看出,随着l由10 nm增加至20 nm和50 nm,频率成比例增大,说明应变梯度效应会增加系统刚度,促进波的传导。
图6显示的是流速与振动频率实部的变化关系。频率的变化规律依然与图5相同,即随着应变梯度参数l的增大,频率也增加,依然是由于应变梯度效应增加系统刚度所致。然而,随着流速增加,频率出现先增加后减小的趋势,即流速有一临界值,在该临界值前后,频率的变化规律相反。该规律和图3类似,当流速较大时,流体分子运动加剧,导致系统内尺度效应增强,波动阻尼增大。但是图6的临界流速与图3不同,该临界流速不是固定值,而随l变大而升高。该现象是由于应变梯度效应会增加系统刚度,所以l值越大越有利于波传导,于是发生阻尼的临界流速也就越高,这一结果也进一步证实了应变梯度效应增加系统刚度的结论。
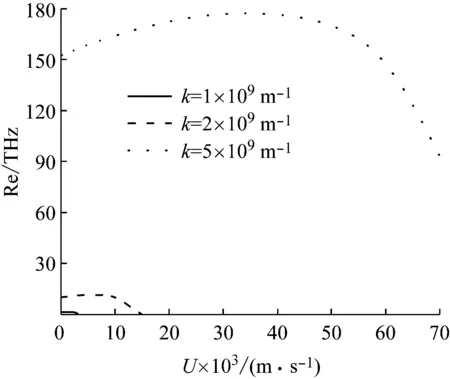
(a) 整体图

(b) 局部图

图5 频率实部与纳观尺度参数和应变尺度参数的变化关系图
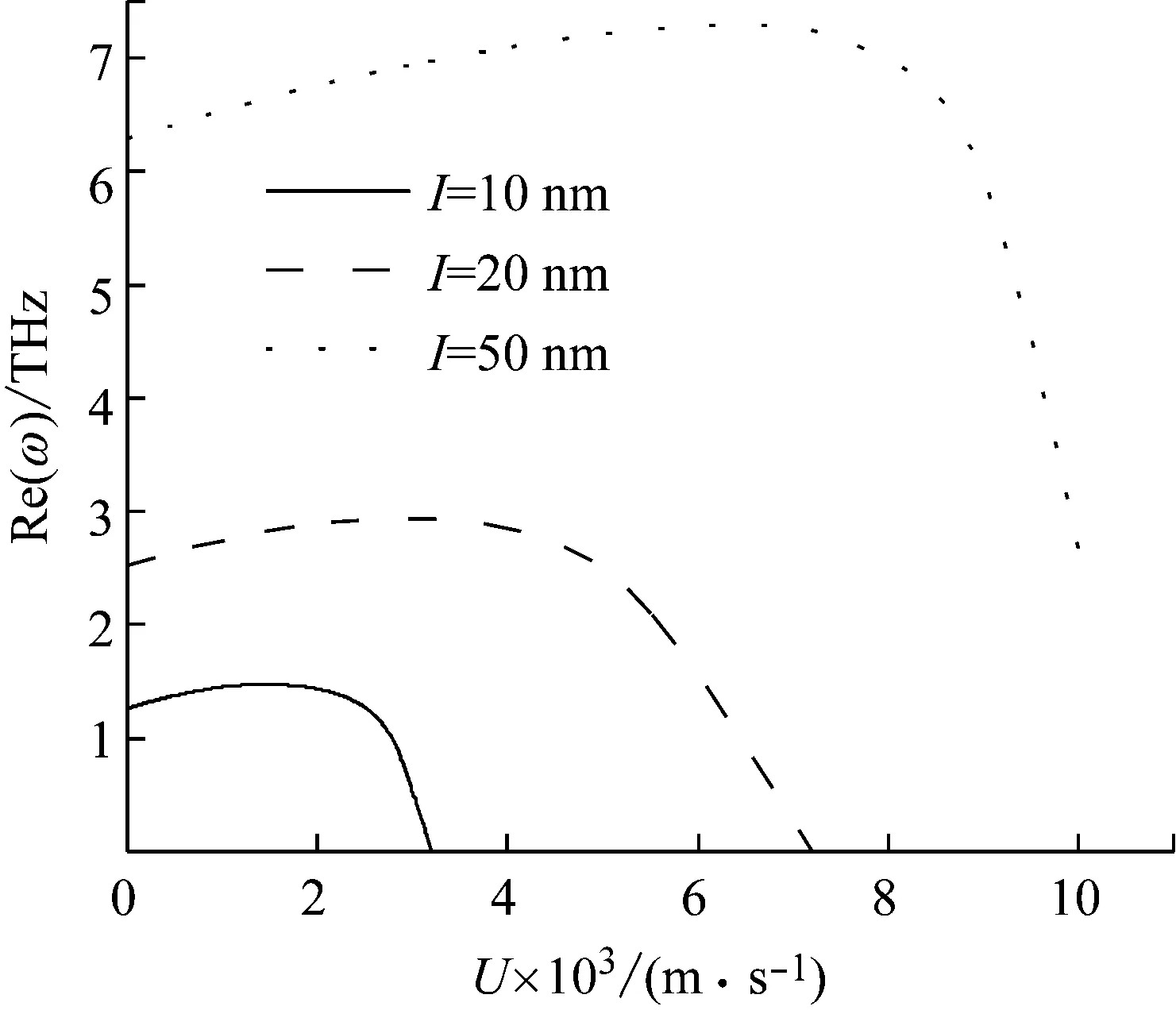
图6 频率实部与流速和应变尺度参数的变化关系图
图7显示了波数与振动频率实部的变化关系。由图7可见,不论应变梯度参数l取值如何,频率最大值总出现在k=18×109m-1时,但随着取值l增加,振动频率的值也相应增大。这也再次证明应变梯度效应将增加系统刚度。进一步观察发现,当波数超过k=20×109m-1时,振动频率的值就退化为虚数,频率实部在图7中已不存在,虚部则由图8呈现。
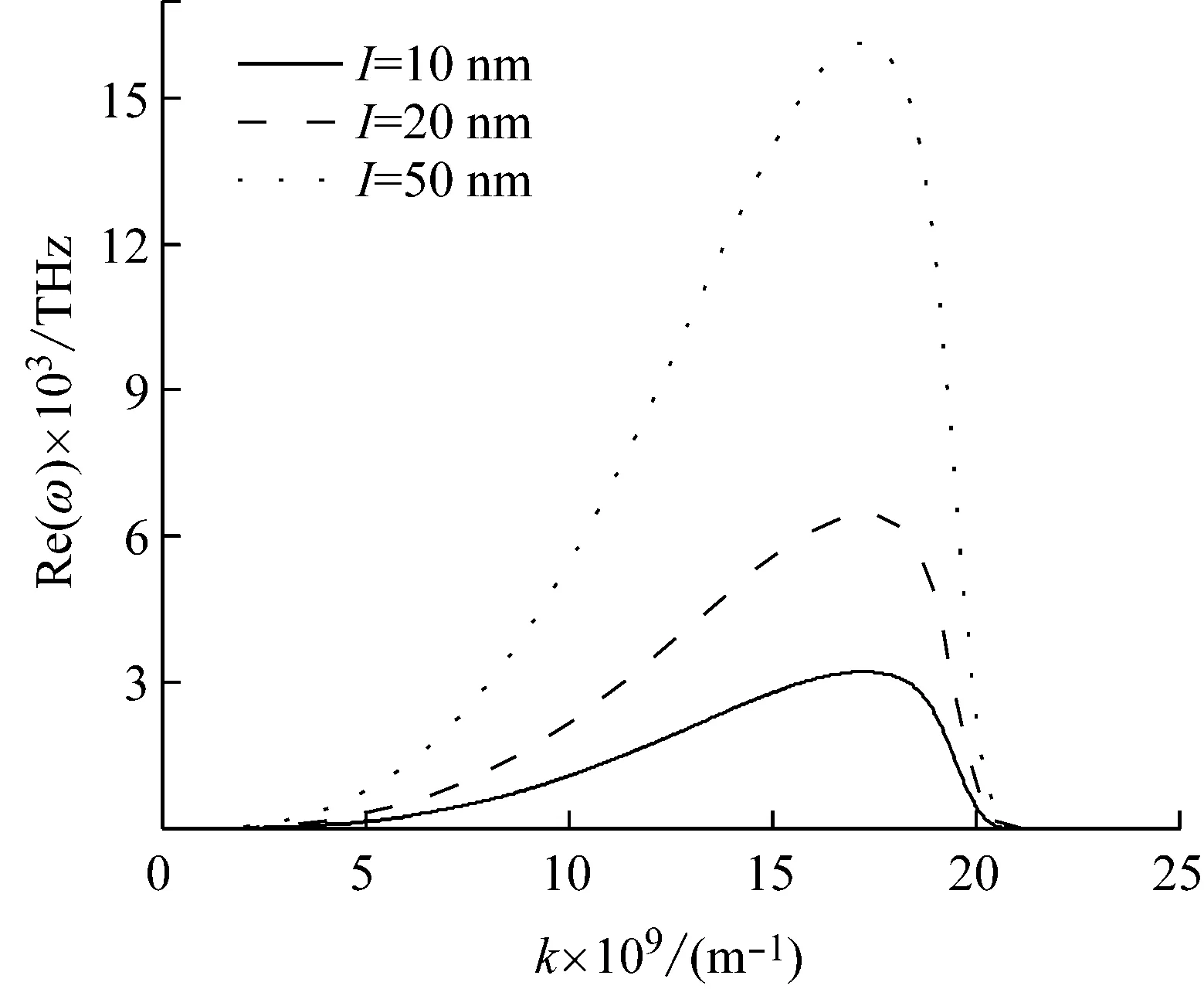
图7 频率实部与波数和应变尺度参数的变化关系图
由图8可以发现频率虚部的变化有两个特征:① 振动频率虚部绝对值随着波数增加而增加,说明继续增加波数减小波长,波的传导将受到阻尼;② 频率虚部随应变梯度参数l增加而升高,说明此时的应变梯度效应不再增加系统刚度,反而阻碍波传导。由以上两点分析,可以得出结论:当波数增加至k=20×109m-1时,波长已经小于应变梯度参数值l,说明一个波动周期无法超出尺度效应影响范围,波的传导将受到尺度效应的阻碍,原理与图2所示一致。
图9显示的是流体边界条件参数Kn和振动频率的变化关系。由图9可见,系统振动频率随流速增加,表现出先增加后衰减的规律。Kn值越大,频率衰减出现越早,在衰减出现之前,Kn取值较大,则频率较高。
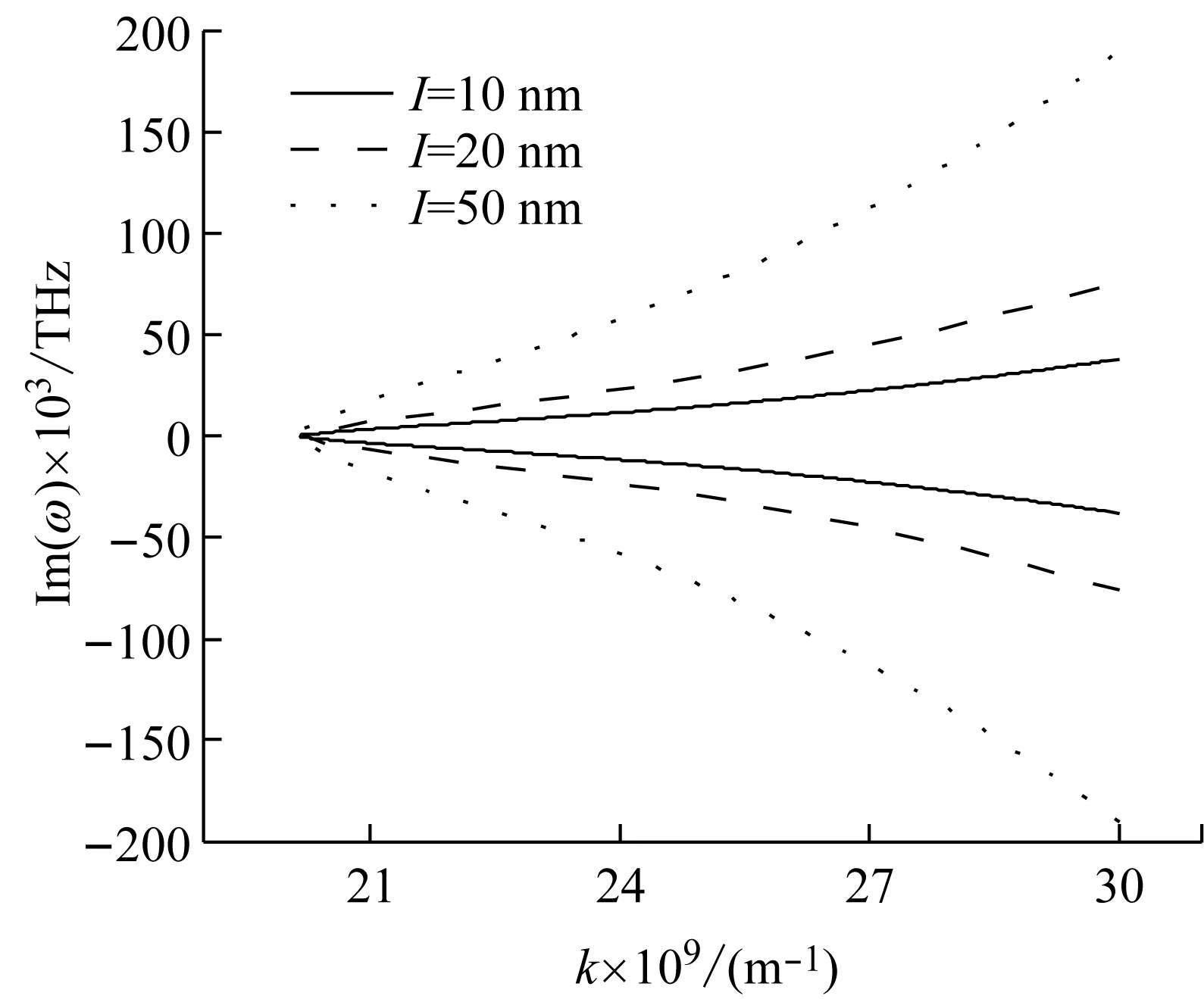
图8 频率虚部与波数和应变尺度参数的变化关系图
对于低流速时频率随Kn值增加而升高,是因为流体尺度效应增加系统刚度所致。而在高流速时较大的Kn值导致较早出现振动衰减,则是因为高流速体系振动频率高,波长范围小于尺度效应影响区域,能量传递受阻,与之前所述固体尺度效应影响规律一致。

图9 Knudsen数取值不同时的频率实部与流速关系图
图10显示的是当波数变化时,Kn取不同的值所对应的Argand图(实部/虚部关系图)。图10中流速为300 m/s,该流速处于图8所示振动出现衰减之前。可以看出,取相同的虚部值,所对应的实部值随着Kn的增加而变大,说明流速相同时,尺度效应越强,振动阻尼出现越迟,反映出流体尺度效应同样可以增加系统刚度,且与固体非局部效应相比,影响更明显。
对于纳米尺度的结构体,数值模拟结果往往缺乏相应的实验数据作为验证和支撑。通常情况下,数值结果的验证都是通过不同理论模型模拟数据的对比来完成。前文已提及,对于非局部应力场理论在碳纳米管动力学特性方面的研究,已有很多结论,证明该模型模拟结果是合理可靠的。作者前期发表的论文中,曾以非局部模型和分子动力学模拟结果进行对比验证,证明非局部模型模拟碳纳米管波动特性的结果与分子动力学模拟结果吻合度很好。对于本文应用的非局部/应变梯度耦合模型,在文献[33]中同样被证明和分子动力学模拟以及其它理论模型模拟结果有较高的吻合度。除此以外,本文以流体边界滑移理论建模,定量分析流体小尺度效应对流速的影响,该方法的合理性同样已在相关文献中得到证实和应用。因此,本文应用的建模理论和方法是得到公认的,模拟结果同样是合理可靠的。
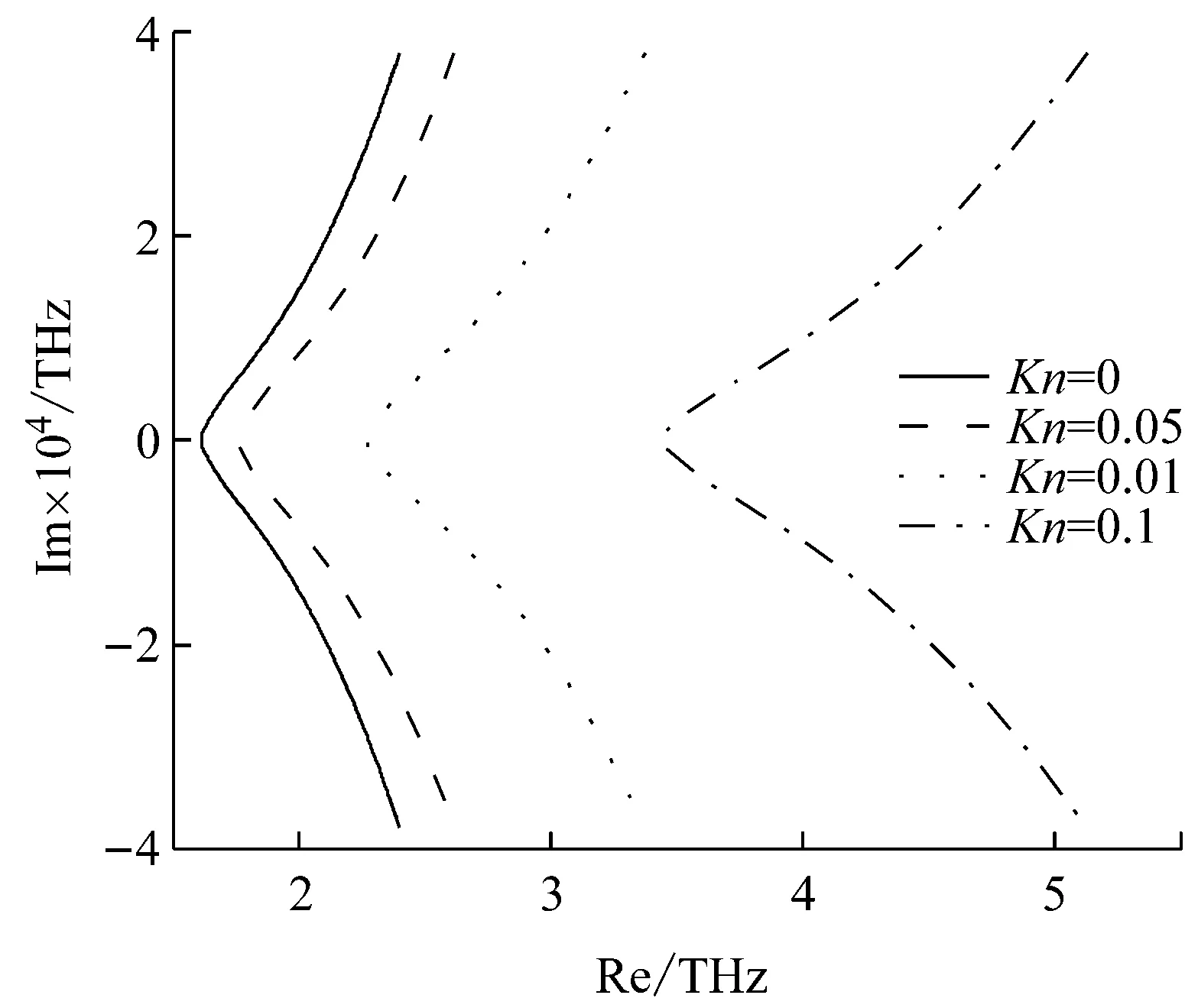
图10 Knudsen数取值不同时的Argand图
4 结论
本文结合非局部应力场理论、应变梯度理论和流体滑移边界理论,建立了充流单壁碳纳米管流固耦合系统的波动模型。分别以三种理论分析碳纳米管和管腔内流体的微纳观尺度效应,推导得到了充流碳纳米管的Euler-Bernoulli梁自由振动控制方程。在对控制方程解析解推导过程中,分别讨论了非局部参数、应力梯度参数和流体边界效应参数对振动频率的影响,得出以下结论:
(1) 对于波长较大,频率较低的波动与振动,碳纳米管的应变梯度效应和流体的滑移边界效应使体系刚度增加,可以促进系统振动和波传导;而碳纳米管应力非局部效应会减小系统刚度,阻碍振动与波动。
(2) 对于波长较小,频率较高的波动与振动,结论(1)中应变梯度效应和流体的滑移边界效应不但无法起到促进作用,反而会有阻尼和衰减作用,而应力非局部效应对振动产生的阻尼作用不变。其原因则是当波长范围小于尺度效应影响范围时,能量传递将受到阻碍。
(3) 三种微尺度效应对流速不同的充流碳纳米管动力特性影响明显,当流速较高时,分子间相互作用力增大,尺度效应增强,而高流速引发的振动波长较小,同样由于波长范围小于尺度效应影响范围,能量传递受阻,振动受到阻尼;而流速较低时,无上述现象,流速增加反而有利于振动和波动。
[1] IIJIMA S. Helical microtubules of graphitic carbon[J]. Nature, 1991,354:56-58.
[2] TREACY M M J, EBBESEN T W, GIBSON T M. Exceptionally high Young’s modulus observed for individual carbon nanotubes[J]. Nature, 1996, 381(6584):678-680.
[3] WONG E W, SHEEHAN P E, LIEBER C M. Nanobeam mechanics elasticity, strength and toughness of nanorods and nanotubes[J]. Science, 1997, 277(5334):1971-1975.
[4] BALL P. Roll up for the revolution[J]. Nature, 1981, 414(6860):142-144.
[5] BAUGHMAN R H, ZAKHIDOV A A, DEHEER W A. Carbon nanotubes—the route toward applications[J]. Science, 2002, 297(5582):787-792.
[6] KRISHNAN T V S, BABU J S. SATHIAN S P. A molecular dynamics study on the effect of thermostat selection on the physical behavior of water molecules inside single walled carbon nanotubes[J]. Journal of Molecular Liquids, 2013, 188(188):42-48.
[7] CUI Jianlei, YANG Lijun, WANG Yang. Molecular dynamics study of the positioned single-walled carbon nanotubes with T-, X-, Y- junction during nanoscale soldering[J]. Applied Surface Science, 2013, 284(11):392-396.
[8] WANG Jifen, XIE Huaqing. Molecular dynamic investigation on the structures and thermal properties of carbon nanotube interfaces[J]. Applied Thermal Engineering, 2015, 88: 35737-35745.
[9] LIEW K M, WONG C H, TAN M J. Buckling properties of carbon nanotube bundles[J]. Applied Physics Letters, 2005, 87(4):041901.
[10] KITIPORNCHAI S, HE X Q, LIEW K M. Buckling analysis of triple-walled carbon nanotubes embedded in an elastic matrix[J]. Journal of Applied Physics, 2005, 97(11):114318.
[11] YAN Y, HE X Q, ZHANG L X. Flow-induced instability of double-walled carbon nanotubes based on an elastic shell model[J]. Journal of Applied Physics, 2007, 102(4):044307.
[12] YAN Y, HE X Q, ZHANG L X, et al. Dynamic behavior of triple-walled carbon nanotubes conveying fluid[J]. Journal of Sound and Vibration, 2009, 319(3/4/5):1003-1018.
[13] YAN Y, HE X Q, ZHANG L X. Dynamical behaviors of fluid-conveyed multi-walled carbon nanotubes[J]. Applied Mathematical Modelling, 2009, 33(3):1430-1440.
[14] YOON J, RU C Q, MIODUCHOWSKI A. Vibration and instability of CNTs conveying fluid[J]. Composites Science and Technology, 2005, 65(9):1326-1336.
[15] YOON J, RU C Q, MIODUCHOWSKI A. Flow-induced flutter instability of cantilever CNTs[J]. International Journal of Solids and Structures, 2006, 43(11):3337-3349.
[16] ERINGEN A C. Nonlocal continuum field theories[M]. New York: Springer, 2002.
[17] BAHAADINI R, HOSSEINI M. Effects of nonlocal elasticity and slip condition on vibration and stability analysis of viscoelastic cantilever carbon nanotubes conveying fluid[J]. Computational Materials Science, 2016, 114:151-159.
[18] ZHEN Yaxin, FANG Bo. Nonlinear vibration of fluid-conveying single-walled carbon nanotubes under harmonic excitation[J]. International Journal of Non-linear Mechanics, 2015, 76:48-55.
[19] ZEIGHAMPOUR H, BENI Y T. Size-dependent vibration of fluid-conveying double-walled carbon nanotubes using couple stress shell theory[J]. Physica E, 2014, 61(26):28-39.
[20] DENG Qingtian, YANG Zhichun. Vibration of fluid-filled multi-walled carbon nanotubes seen via nonlocal elasticity theory[J]. Acta Mechanica Solida Sinica, 2014, 27(6):568-578
[21] FILIZ S, AYDOGDU M. Wave propagation analysis of embedded (coupled) functionally graded nanotubes conveying fluid[J]. Composite Structures, 2015, 132:1260-1273.
[22] LI Li, HU Yujin. Wave propagation in fluid-conveying viscoelastic carbon nanotubes based on nonlocal strain gradient theory[J]. Computational Materials Science, 2016, 112:282-288.
[23] ALI-ASGARI M, MIRDAMADIN H R, GHAYOUR M. Coupled effects of nano-size, stretching, and slip boundary conditions on nonlinear vibrations of nano-tube conveying fluid by the homotopy analysis method[J]. Physical E, 2013, 52(4):77-85.
[24] ASKES H, SUIKE A S J, SLUYS L J. A classification of high order strain gradient models-linear analysis[J]. Achieve of Applied Mechanics, 2002, 72(72):171-188.
[25] AIFANTIS E C. Strain gradient interpretation of size effect[J]. International Journal of Fracture, 1999, 95: 299-314.
[26] AIFANTIS E C. Gradient deformation models at nano micro and macro scales[J]. Journal of Engineering Material Technology, 1999, 121: 189-202.
[27] PEDDIESON J, BUCHANAN G R, MCNITT R P. Application of nonlocal continuum models to nanotechnology[J]. International Journal of Engineering Science, 2003, 41(3/4/5): 305-312.
[28] WANG Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics[J]. Journal of Applied Physics, 2005, 98(12):124301.
[29] CHEN B, GAO M, ZUO J M, et al. Binding energy of parallel carbon nanotubes[J]. Applied Physics Letters, 2003, 83: 3570-3571.
[30] CHALLAMEL N. Variational formulation of gradient or/and nonlocal higher-order shear elasticity beams[J]. Composite Structures, 2013,105: 351-368.
[31] SONG J, SHEN J, LI X F. Effects of initial axial stress on waves propagating in carbon nanotubes using a generalized nonlocal model[J]. Computational Materials Science, 2010, 49(3):518-523.
[32] SHEN J, WU J X, SONG J. Flexural waves of carbon nanotubes based on generalized gradient elasticity[J]. Physica Status Solid B, 2012, 249(1):50-57.
[33] LIM C W, ZHANG G, REDDY J N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation[J]. Journal of the Mechanics and Physics of Solids, 2015, 78:298-313.
[34] LI Li, HU Yujin. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory[J]. International Journal of Engineering Science, 2015, 97:84-94.
[35] LI Li, HU Yujin, LING Ling. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory[J]. Composite Structures, 2015, 133:1079-1092.
[36] LI Li, HU Yujin, LING Ling. Wave propagation in viscoelastic single-walled carbon nanotubes with surface effect under magneticfield based on nonlocal strain gradient theory[J]. Physica E, 2016, 75:118-124.
[37] PAIDOUSSIS M P. Fluid-structure interactions slender structures and axial flow[M]. San Diego: Academic Press, 1998.
[38] 林建忠,微纳流动理论和应用[M]. 北京:科学出版社,2010.
[39] RASHIDI V, MIRDAMADI H R. A novel model for vibrations of nanotubes conveying nanoflow[J]. Computational Material Science, 2012, 51(51):347-352.
[40] MIRRAMEZANI M, MIRDAMADI H R. The effects of Knudsen-dependent flow velocity on vibrations of a nano-pipe conveying fluid[J]. Archive of Applied Mechanics, 2012, 82(7):879-890.
[41] MIRRAMEZANI M, MIRDAMADI H R. Effects of nonlocal elasticity and Knudsen number on fluid-structure interaction in carbon nanotube conveying fluid[J]. Physica E, 2012, 44(10):2005-2015.
[42] YANG Y, LIM C W. Wave propagation in carbon nanotubes nonlocal elasticity-induced stiffness and velocity enhancement effects[J]. Journal of Mechanics of Materials and Structures, 2010, 5(3):459-476.
[43] LIM C W, YANG Y. Nonlocal elasticity for wave propagation in carbon nanotubes: the physics and new prediction of nanoscale in nonlocal stress field[J]. Journal of Computational and Theoretical Nanoscience, 2010, 7(6): 988-995
[44] YANG Y, ZHANG L X, LIM C W. Wave propagation in fluid-filled single-walled carbon nanotube on analytically nonlocal Euler-Bernoulli beam model[J]. Journal of Sound and Vibration, 2012, 331(7):1567-1579.
Wave propagation of fluid-filled single-walled carbon nanotubes based on the nonlocal-strain gradient theory
YU Yang, YANG Yang
(Department of Engineering Mechanics, Kunming University of Science and Technology, Kunming 650500, China)
Based on the high-order nonlocal strain gradient theory and slip boundary conditions of nano-scale fluid, a dynamic model of Euler-Bernoulli beams for fluid-filled single-walled carbon nanotubes (SWCNT) was established. The governing equation of wave propagation for fluid filled SWCNT beams was derived according to the Hamilton’s principle. By solving the governing equations, analytical expressions of angular frequency for dynamic systems were obtained, and the influence from nano-scale effects on dynamic behaviors of SWCNTs were studied. According to the simulation results, wave propagation with low wavelength are enhanced by strain gradient and fluid slip boundary effects when the ones with high wavelength are damped. The nonlocal stress effect only contributes to the decay of the dynamic behaviors for any wavelength. These three scale effects lead to stiffness enhancement for fluid filled SWCNTs at low fluid velocity when wave propagation are promoted. However, the wave propagation behaviors are damped at high fluid velocity, since energy transmission in this case is damped by the scale effects.
nonlocal stress; strain gradient; nanotube; fluid boundary effect; Euler-Bernoulli beam; wave propagation
国家自然基金(11462010; 11261026)
2016-06-27 修改稿收到日期:2016-08-23
余阳 男,硕士生,1991年生
杨洋 男,博士,副教授,1981年生 E-mail:yangyang0416@kmust.edu.cn
TH212; TH213.3
A
10.13465/j.cnki.jvs.2017.08.001
