波形钢腹板PC简支箱梁桥局部与整体动力冲击系数的计算分析

冀 伟， 邓 露， 何 维， 刘世忠， 蔺鹏臻

(1. 兰州交通大学 土木工程学院, 兰州 730070； 2. 湖南大学 土木工程学院， 长沙 410082)

波形钢腹板PC简支箱梁桥局部与整体动力冲击系数的计算分析

冀 伟1，2， 邓 露2， 何 维2， 刘世忠1， 蔺鹏臻1

(1. 兰州交通大学 土木工程学院, 兰州 730070； 2. 湖南大学 土木工程学院， 长沙 410082)

为合理分析和计算波形钢腹板PC简支箱梁桥局部与整体的动力冲击系数，分别建立了波形钢腹板PC箱梁桥和车辆结构的振动方程，并根据车轮与桥面的接触关系形成两者耦合振动的动力方程。采用MATLAB和ANSYS软件分别建立了三维的车辆模型和波形钢腹板PC箱梁桥的有限元模型，并在考虑路面平整度随机激励的作用下，利用MATLAB软件求解了车桥耦合系统的动力方程，得到桥梁结点的位移振动响应；依据动位移与静位移的关系，计算出了波形钢腹板PC箱梁桥的局部及整体的动力冲击系数；对所求得的局部及整体动力冲击系数进行了不同车辆类型、不同车道数加载，不同行驶速度和不同路面情况下的参数分析，并与我国现行规范和美国现行AASHTO规范进行对比分析，最终提出了波形钢腹板PC简支箱梁桥局部及整体动力冲击系数的合理确定方法，所得结论可为波形钢腹板PC箱梁桥动力冲击系数的确定提供参考。

波形钢腹板； 组合箱梁； 车桥耦合振动； 动力冲击系数； 路面平整度

波形钢腹板PC箱梁桥是一种新型的钢-混组合桥梁结构，其明显特点是用10 mm左右厚的波形钢腹板取代30～80 mm厚的混凝土腹板[1]，并通过体内和体外预应力筋对梁体施加预应力。该桥型大幅度减轻了梁体的自重，提高了混凝土翼板的预应力施加效率，另外由于波形钢腹板的特殊构造，其抗剪强度与平腹钢板相比有较大提高。由于该桥型具有诸多优点，其已在国内外的桥梁建设中得到了越来越广泛的应用。

目前，国外学者针对波形钢板及波形钢腹板I型钢梁的抗弯性能[2]，剪切强度[3]、弯扭屈曲性能[4]及手风琴效应[5]等内容进行了分析；国内学者主要对波形钢腹板PC箱梁桥的抗扭性能[6]、剪滞效应分析[7]及挠度计算[8]等静力学性能进行了研究。此外，国内学者在波形钢腹板PC箱梁桥动力特性方面的研究也取得一些研究成果，但研究成果主要针对其弯曲振动及扭转振动特性的分析[9-11]，对车辆荷载作用下波形钢腹板PC箱梁桥动力冲击系数的研究相对较少[12]。动力冲击系数(IM)是桥梁设计中用以表征车辆过桥时对桥梁结构产生的竖向动力效应的增大系数，是桥梁设计过程中的一个非常重要的指标，也是桥梁状况评估时的一个重要参数，其定义为

(1)

式中：ydmax为桥梁结构的最大动位移，ysmax为桥梁结构的最大静位移。

目前，我国现行规范中还没有明确波形钢腹板PC箱梁桥的动力冲击系数该如何取值。虽然《公路桥涵设计通用规范》JTG D60—2015[13]介绍了桥梁冲击系数的计算方法，即规定采用桥梁结构的基频来估算整体的动力冲击系数和对于汽车荷载的局部加载及在T梁、箱梁悬臂板上的局部冲击系数采用0.3，但规范定义的整体与局部动力冲击系数是否适用波形钢腹板PC箱梁桥还待进一步研究。

因此，本文基于车桥耦合振动理论，利用数值模拟技术计算了跨径为30 m的单箱单室波形钢腹板PC简支箱梁桥在移动车辆荷载作用下整体和局部的动力冲击系数，并对比了车辆类型、行驶车道数、行驶速度和路面平整度等多个影响局部和整体动力冲击系数的因素进行了参数分析。最后将车桥耦合振动分析所得的动力冲击系数与不同规范下定义的动力冲击系数进行对比分析，以考察规范定义动力冲击系数的安全性，并得到一些有意义的结论，所得结论可为我国波形钢腹板PC箱梁桥动力冲击系数的确定提供参考。

1 波形钢腹板PC简支箱梁桥的原型

本文单箱单室波形钢腹板PC简支箱梁桥的截面尺寸是结合我国已建重庆永川大堰河桥 (国内首座波形钢腹板箱梁简支公路梁桥)和日本新开桥的设计尺寸给出的，如图1所示。

桥梁设计跨径为30.4 m，计算跨径为30.0 m，桥面为7.0 m+2×1.0 m= 9.0 m。沿桥纵向设置了2道中横隔板和2道端横隔板以提高波形钢腹板PC箱梁桥的抗扭性能。主梁采用C50混凝土，波形钢腹板采用Q345c钢板，厚9 mm，其几何尺寸如图2所示。

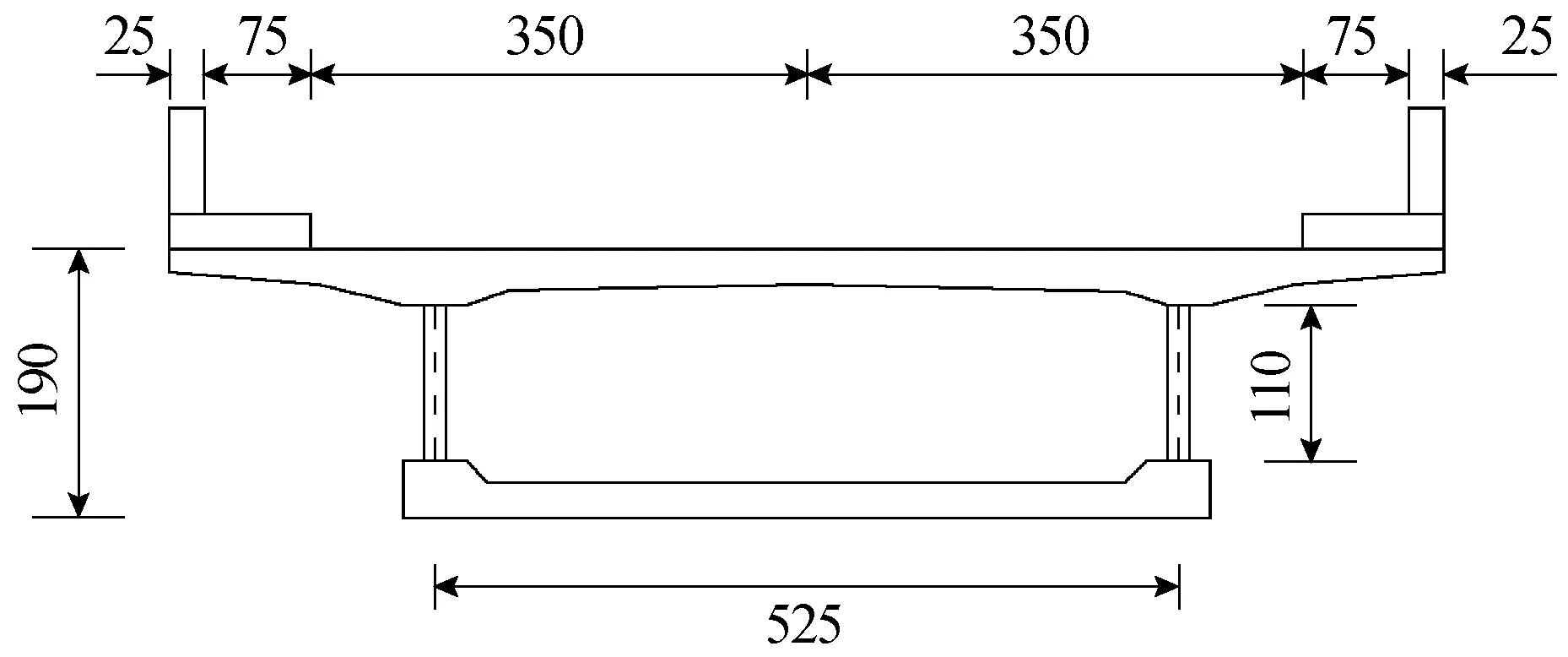
图1 横截面布置图(cm)

图2 波形钢腹板的几何尺寸(mm)

采用ANSYS 14.0有限元软件建立波形钢腹板PC简支箱梁桥的有限元模型，钢筋混凝土材料的上、下翼板及横隔板采用实体单元SOLID45来建立，波形钢腹板采用壳单元SHELL63来建立。波形钢腹板与混凝土上、下翼板的连接处采用刚性连接，即波形钢腹板的节点与翼板的节点在相应位置处耦合竖向、横向及纵向自由度，形成刚性连接，如图3所示。

波形钢腹板PC简支箱梁桥的边界为一端活动铰支座，约束梁的竖向、横向位移，另一端为固定铰支座，约束梁的竖向、纵向和横向位移。建立好的有限元模型如图4所示。

图4 波形钢腹板PC简支箱梁的有限元模型

为验证有限元模型的正确性，参考文献[14]中提出的一种求解波形钢腹板PC简支箱梁桥弯曲振动频率的改进公式，见式(2)：

f=

(2)

将ANSYS有限元计算的前两阶弯曲振动频率与式(2)的计算值进行对比分析(如表1所示)，两者吻合良好，验证了有限元模型的正确性。

表1 波形钢腹板PC简支箱梁桥自振频率对比

2 车辆模型的建立

车辆类型、车重、轴数及基频等车辆参数对波形钢腹板PC箱梁桥的动力冲击系数具有重要的影响，本文选用了国内外学者在车桥耦合振动研究中广泛采用的两种车辆模型[15-16]。这两种车辆模型的参数均得到了较为深入的验证，车辆悬挂系统参数合理，且车辆轴数、轴重、轴距等参数具有较好的代表性。车辆模型的几何示意图见图5和6，详细参数见表2。

表2 研究用两种车辆模型详细参数

3 路面平整度模拟

在美国AASHTO LRFD规范中规定[17]，路面的平整度是车桥耦合振动动力响应的一个重要激励源。目前对路面平整度进行数值模拟时，通常采用文献[18]提出的功率谱密度函数：

(3)

式中：n为空间频率，单位为 cycle/m；n0为标准空间频率，n0=1/(2π)，单位为 cycle/m，为空间频率的低频段与高频段的分界；φ(n0)是标准空间频率对应的路面粗糙系数，单位为 m3/cycle，其值决定了路面的平顺程度。n1和n2是路面功率谱在低频段和高频段分别采用不同的指数。

使用级数方法可生成功率谱函数的路面平整度曲线，其公式为

(4)

式中：x为桥长方向的坐标，nk为空间频率采样点，单位为cycle/m；Δn为空间频率采样间距；N为空间频率采样数；θk为在(0，2π)区间上的随机相位角。

国际标准化组织(ISO，1995)将路面平整度从非常差(Very poor)到非常好(Very good)分为5级[19]。本文采用其中路面平整度为好、中、差的三种路面。图7所示的为一组路面平整度曲线。

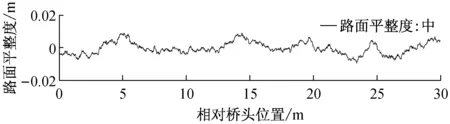
图7 路面平整度的样本曲线

4 车桥耦合方程的建立

为建立波形钢腹板PC箱梁桥和车辆结构的耦合方程，首先分别建立了两者各自的振动方程，如式(5)和式(6)所示：

(5)

(6)

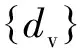
依据车轮和桥面接触点的位移和相互作用力关系，可将式(5)与式(6)写成如下的耦合方程[20]：

(7)

式中：Cb-b，Cb-v，Cv-b,Kb-b,Kb-v，Kv-b，Fb-r，Fv-r是由于车桥耦合效应产生的附加项。当车辆通过桥梁时，接触点的路面平整度和接触力是随时间变化的，因此式(7)是也是随时间变化的。为了计算过程的简单性，在获得桥梁结构的自振频率和振型后，可采用振型叠加法对式(7)进行化简。桥梁的位移向量可表示为

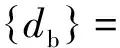
(8)

(9)

式中I为单位矩阵，化简后的车桥耦合振动方程的复杂性将大大降低，采用MATLAB软件编制四阶龙格库塔方法求解方程式(9)便可以获得桥梁在车桥耦合振动作用下的动位移，结合式(1)便可求得桥梁的动力冲击系数。

5 动力冲击系数的计算与分析

5.1 工况设定

本文所编制的车桥耦合振动计算程序可以计算不同参数(车重、轴距、速度、路面平整度等)下车桥耦合系统的动力响应。程序的正确性已在文献[20]中将数值模型的计算结果和实桥的测试数据进行了对比分析，两者吻合良好，验证了所编制计算程序的正确性。本文选择了波形钢腹板PC简支箱梁桥跨中截面的8个位置点(如图8所示)来计算分析其局部与整体动力冲击系数。图8中Li(i=1,2,3,4,5)用于桥梁结构局部冲击系数的计算；Gi(i=1,2,3)用于桥梁结构整体冲击系数的计算。冲击系数的计算工况如表3所示。

图8 测点与车辆加载位置

表3 冲击系数的计算工况

图9所示为典型的在车桥耦合作用下波形钢腹板PC简支箱梁桥跨中截面G2点的位移响应曲线，分别提取动、静位移曲线上的最大值，即可按式(1)计算其动力冲击系数。

图9 典型跨中挠度响应曲线(路面好，2#车，G2点，车速90 km/h)

5.2 行车速度与动力冲击系数的关系

由于路面平整度为随机过程，生成的路面平整度曲线有较大随机性，掩盖了动力冲击系数的本质规律，解决办法的通常采用多个平整度样本进行计算以获得桥梁结构多个动力响应值，最后求其平均值，以降低路面随机性的影响，一般20个平整度样本即可以达到满意的结果。采用本文编制的车桥耦合振动计算程序求得了表3所示工况下的波形钢腹板PC简支箱梁桥局部与整体的动力冲击系数。将1#车和2#车在同种速度下，三种路面平整度对应的冲击系数求平均值，获得其局部和整体动力冲击系数随车速的变化情况，如图10和11所示。

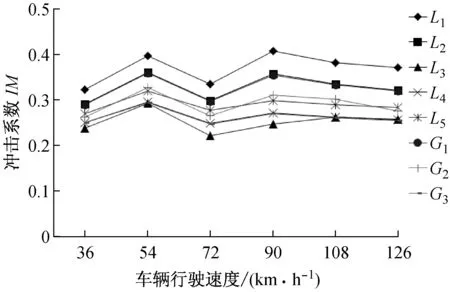
(a) 1#车单车行驶

(b) 2#车单车行驶

由图10可知，1#车和2#车单车行驶时，波形钢腹板PC简支箱梁桥最大的局部动力冲击系数要高于最大的整体冲击系数。

1#车和2#车单车行驶时，计算出的局部冲击系数L1>L2>L5>L4>L3，即悬臂板的局部冲击系数最大，腹板与顶板交界处次之，箱中顶板中心处最小；计算出的整体冲击系数G1>G2>G3，即远离车辆加载位置处的腹板与底板交界处的整体冲击系数最大，箱中底板中心处次之，靠近车辆加载位置处的腹板与底板交界处的最小。

由图11可以看出，双车行驶时，波形钢腹板PC箱梁桥最大的局部动力冲击系数要低于最大的整体冲击系数。对于1#车双车行驶时，由于对称性(L1=L5)> (L2=L4)>L3，即悬臂板的局部冲击系数最大，腹板与顶板交界处次之，箱中顶板中心处最小；整体冲击系数G2>(G1=G3)，即箱中底板中心处最大，腹板与底板交界处的最小。对于2#车双车行驶时，悬臂板的局部冲击系数最大，整体冲击系数在箱中底板中心处最大，腹板与底板交界处的最小。

结合图10和11可知，对于1#车单车和双车行驶时，冲击系数随速度的增加呈现出增大-减小-增大-减小的趋势，冲击系数最大值易出现在车速较高的时候。对于2车单车和双车行驶时，冲击系数随速度的增加呈现出先减小，后增大的趋势，冲击系数最大值易出现在车速较低的时候。

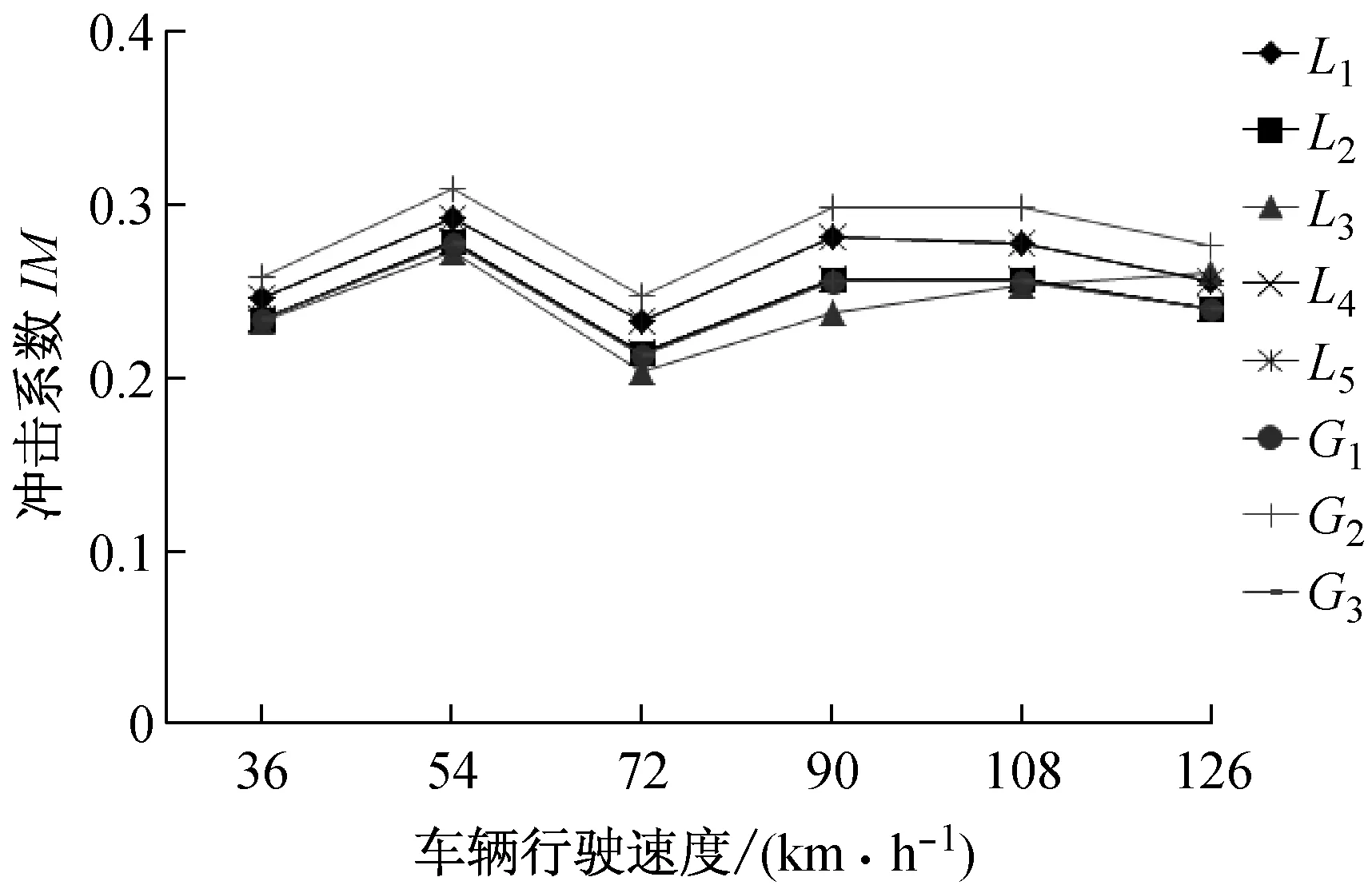
(a) 1#车双车行驶

(b) 2#车双车行驶

5.3 路面平整度与动力冲击系数的关系

1#车和2#车在波形钢腹板PC箱梁桥上行驶，行驶方式为单车和双车行驶，每种车辆在不同路面平整度下分别有六种行驶速度，将1#车和2#车在不同路面平整度下的六种速度的动力冲击系数求均值，得到随路面平整度变化的动力冲击系数，见表4。

由表4可知，单车行驶下波形钢腹板PC箱梁桥局部与整体的动力冲击系数要大于双车行驶的情况，为使计算的局部与整体动力冲击系数偏于安全，宜采用单车行驶下求得的动力冲击系数。

单车和双车行驶下，波形钢腹板PC简支箱梁桥局部与整体的动力冲击均随着路面平整度的好转而减小，说明路面平整度的好坏对其动力冲击系数有较大影响。

5.4 与规范的比较

我国现行规范中尚未有单独考虑波形钢腹板PC箱梁桥冲击系数的计算。采用《公路桥涵设计通用规范》JTG D60—2015中桥梁基频计算本文波形钢腹板PC箱梁桥的动力冲击系数，所得的整体动力冲击系数为0.235；对于汽车荷载的局部加载及在T梁、箱梁悬臂板上的冲击系数采用0.3，因此规范定义的局部冲击系数为0.3。将规范所得的局部与整体动力冲击系数与表4对比可以看出：在路面为一般和好的情况下，规范取值基本是适用于波形钢腹板PC简支箱梁桥的；对于路面差的情况下，规范的取值偏小。

表4 动力冲击系数与路面平整度之间的关系

与美国现行AASHTO规范对比可以看出：在路面为中和好的情况下，两种车型对应的局部和整体动力冲击系数均比美国规范值0.33偏低；而在路面为差的情况下，波形钢腹板PC箱梁桥的动力冲击系数同样比美国规范值总体偏高。

6 结 论

本文基于车桥耦合振动理论，利用数值模拟技术计算了跨径为30 m的单箱单室波形钢腹板PC简支箱梁桥在移动车辆荷载作用下整体与局部的动力冲击系数，通过分析可得如下结论：

(1) 车辆单车行驶下，波形钢腹板PC简支箱梁桥最大的局部动力冲击系数要高于最大的整体冲击系数；双车道行驶时，情况相反。

(2) 车辆单车及双车行驶下，计算出的局部冲击系数最大值均出现在悬臂板处，最小值均出现在箱中顶板中心处。

(3) 车辆单车行驶下，计算出的整体冲击系数最大值出现在远离车辆加载位置的腹板与底板交界处；车辆双车行驶下，计算出的整体冲击系数最大值出现在箱中底板中心处。

(4) 对于不同车型，冲击系数随速度的增加呈现出不同的变化规律。

(5) 在不同路面平整度下，车辆单车行驶下波形钢腹板PC简支箱梁桥局部与整体的动力冲击系数要大于双车行驶的情况，而且路面平整度的好坏对动力冲击的影响较大。

(6) 与中国规范和美国规范定义的局部与整体动力冲击系数对比后发现，在路面平整度为一般和好的情况下，中国及美国规范取值基本上是适用于波形钢腹板PC箱梁桥的；而对于路面平整度为差的情况下，宜采用车桥耦合计算程序计算其动力冲击系数。

桥梁设计中冲击系数的选取还与其静力设计荷载有关系。有时设计静力荷载取值远大于运营荷载，即使冲击系数偏小，依然能够保证结构安全。因此应当通过数值模拟和现场试验相结合的方式来获得比较准确客观的动力冲击系数的统计特性，通过概率和可靠度分析方法选用科学合理的冲击系数，以保证桥梁结构安全。

[1] 陈宜言. 波形钢腹板预应力混凝土桥设计与施工[M]. 北京: 人民交通出版社, 2009.

[2] NGUYEN N D, HAN S R, KIM J H, et al. Moment modification factors of I-girder with trapezoidal web corrugations under moment gradient[J]. Thin-Walled Structures, 2012, 57: 1-12.

[3] HASSANEIN M F, KHAROOB O F. Shear buckling behavior of tapered bridge girders with steel corrugated webs[J]. Engineering Structures, 2014, 74: 157-169.

[4] NGUYEN N D, KIM S N, HAN S R, et al. Elastic lateral-torsional buckling strength of I-girder with trapezoidal web corrugations using a new warping constant under uniform moment[J]. Engineering Structures, 2010, 32: 2157-2165.

[5] OH J Y, LEE D H, KIM K S. Accordion effect of prestressed steel beams with corrugated webs[J]. Thin-Walled Structures, 2012, 57: 49-61.

[6] 江克斌, 丁勇, 杨建奎,等. 波形钢腹板PC组合箱梁纯扭作用下抗扭承载力试验研究[J]. 工程力学, 2013, 30(6): 175-182.

JIANG Kebin, DING Yong, YANG Jiankui, et a1. Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion[J]. Engineering Mechanics, 2013, 30(6): 175-182.

[7] 吴文清, 万水, 叶见曙,等. 波形钢腹板组合箱梁剪力滞效应的空间有限元分析[J]. 土木工程学报, 2004, 37(9): 31-36.

WU Wenqing, WAN Shui, YE Jianshu, et a1. 3D finite element analysis on shear lag effect in composite box girder with corrugated steel web[J]. China Civil Engineering Journal, 2004, 37(9): 31-36.

[8] 刘保东, 任红伟, 李鹏飞. 考虑波纹钢腹板箱梁特点的挠度分析[J]. 中国铁道科学, 2011, 32(3): 21-26.

LIU Baodong, REN Hongwei, LI Pengfei. Deflection analysis considering the characteristics of box girder with corrugated steel webs[J]. China Railway Science, 2011, 32(3): 21-26.

[9] 刘保东, 陈海波, 任红伟. 波形钢腹板混凝土箱梁动力特性改善研究[J]. 中国铁道科学, 2008, 29(3): 29-33.

LIU Baodong, CHEN Haibo, REN Hongwei. Improvement study of the dynamic characteristics for concrete box-girder with corrugated steel webs[J]. China Railway Science, 2008, 29(3): 29-33.

[10] 韦忠瑄, 孙鹰, 沈庆,等. 波形钢腹板PC组合箱梁的动力特性研究. 固体力学学报, 2011, 32: 394-398.

WEI Zhongxuan, SUN Ying, SHEN Qing, et al. Study on dynamic properties of the prestressed concrete box-girder with corrugated steel webs.[J]. Chinese Journal of Solid Mechanics, 2011, 32: 394-398.

[11] 李波, 刘保东, 李鹏飞,等. 波纹钢腹板组合箱梁应力相关阻尼特性研究. 振动与冲击, 2012, 31(6): 68-71.

LI Bo, LIU Baodong, LI Pengfei, et al. Stress-related damping characteristic of a composite box-girder with corrugated steel webs[J]. Journal of Vibration and Shock, 2012, 31(6): 68-71.

[12] 陈志兴. 波形钢腹板箱梁桥车桥耦合振动冲击系数研究[J].山西建筑, 2014, 40(13): 176-178.

CHEN Zhixing. Study on impact coefficient of coupling vibration of vehicle bridge girder bridge with corrugated steel web box[J]. Shanxi Architecture, 2014, 40(13): 176-178.

[13] 公路桥涵设计通用规范：JTG D60—2015[S]. 北京: 人民交通出版社, 2015.

[14] 冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板组合箱梁振动频率分析与试验[J]. 中国公路学报, 2013, 26(5): 102-107.

JI Wei, LIU Shizhong, LIN Pengzhen. Study on influencing factors of vertical frequency of the box girder with corrugated steel webs[J]. China Journal of Highway and Transport, 2013, 26(5): 102-107.

[15] DENG L, CAI C S. Identification of parameters of vehicles moving on bridges[J]. Engineering Structures, 2009, 31(10):2474-2485.

[16] DENG L, CAI C S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges[J]. Engineering Structures, 2010, 32(1): 21-31.

[17] American Association of State Highway and Transportation Officials (AASHTO). LRFD bridge design specifications[S]. Washington DC, 2012.

[18] WANG T, HUANG D. Cable-stayed bridge vibration due to road surface roughness[J]. Journal of Structural Engineering, 1992, 118: 1354-1374.

[19] International Organization for Standard (ISO). Mechanical vibration—road surface profiles—reporting of measured data: ISO 8068[S]. Geneva, 1995.

[20] DENG L. System identification of bridge and vehicle based on their coupled vibration[D]. Baton Rouge, LA: Louisiana State University, 2009.

Local and global impact factors analysis for PC box girder bridges with corrugated steel webs

JI Wei1,2, DENG Lu2, HE Wei2, LIU Shizhong1, LIN Pengzhen1

(1. College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China；2. College of Civil Engineering, Hunan University, Changsha 410082, China)

In order to calculate and analyze the local and global impact factors (IMs) of a simply supported box girder bridge with corrugated steel webs (CSWs) accurately, the motion equations of the bridge and vehicle were established. The two system equations were coupled through the contact condition. Three dimensional vehicle models were established by using the MATLAB software and the finite element model of the PC box girder bridge with CSWs was established by using the ANSYS software, respectively. Considering the random excitation effects of the road roughness, the vibration responses of the bridge nodes could be obtained by using the MATLAB program to solve the dynamic equations of the vehicle-bridge system. According to the relationship between the dynamic and the static deflection, the local and global IMs of the PC box girder bridge with CSWs could be calculated. The obtained local and global IMs were compared and the relationship between the obtained IM and four important parameters, including the type of vehicle, the number of the loaded lanes, vehicle speed, and the road surface condition, was studied. The obtained local and global IMs were also compared with the China code JTG D60—2015 and the AASHTO standard specification. Finally, the reasonable determination method to calculate the local and global dynamic IMs of a simple supported PC box girder bridge with CSWs was presented. The conclusions can provide a reference for determining IMs of this type of bridges.

corrugated steel web; composite box girder; vehicle-bridge interaction; dynamic impact factor; road roughness

国家自然科学基金(51368032; 51208242)；中国博士后科学基金(2014M562103)；甘肃省高等学校科研项目(2015A-053)；甘肃省基础研究创新群体项目资助(1506RJIA029)

2015-12-30 修改稿收到日期：2016-03-18

冀伟 男，博士，副教授，1982年生

E-mail: jiwei1668@163.com

U441+.3

A

10.13465/j.cnki.jvs.2017.08.004